Решение задач на нахождение расстояний в пространстве
Для решения задач на нахождение расстояний в пространстве нужно знать несколько формул и уметь применять их в различных ситуациях.
Формула расстояния между двумя точками в пространстве
Формула для нахождения расстояния между двумя точками в пространстве выглядит следующим образом:
d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²)
где (x₁, y₁, z₁) и (x₂, y₂, z₂) — координаты двух точек в пространстве.
Пример решения задачи на нахождение расстояния между двумя точками в пространстве
Даны точки A(1, 2, -3) и B(4, -1, 2). Найти расстояние между ними.
- Найдем разности координат:
| (x₂ — x₁)²: | (4 — 1)² = 9 |
| (y₂ — y₁)²: | (-1 — 2)² = 9 |
| (z₂ — z₁)²: | (2 -(-3))² = 25 |
- Подставим полученные значения в формулу:
d = √(9 + 9 + 25) ≈ 5,83
Ответ: расстояние между точками A и B ≈ 5,83.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
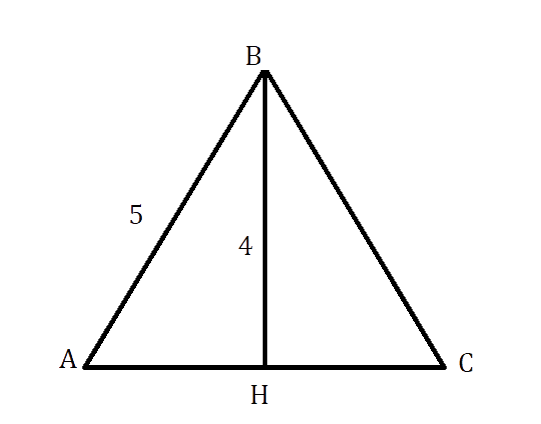
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора \см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
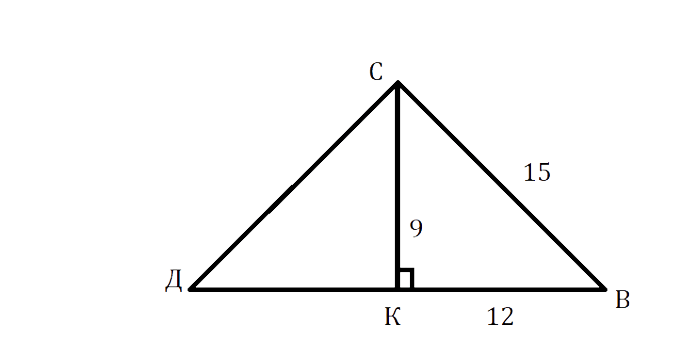
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
\см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
P = a + b + c.
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Далее рассчитывайте Р по такой формуле:
.
Периметр разностороннего треугольника
К разносторонним относятся треугольники, которые не являются равносторонними, равнобедренными или прямоугольными.
Примечание 1
Иногда для подобных треугольников используют определение «произвольный».
Периметр разностороннего треугольника можно высчитать по:
- по трем сторонам;
- по средним линиям;
- по двум ребрам и углу между ними;
- по радиусу вписанной в треугольник окружности.
Укажем формулы для каждого из приведенных способов.
Вычисление периметра по трем сторонам
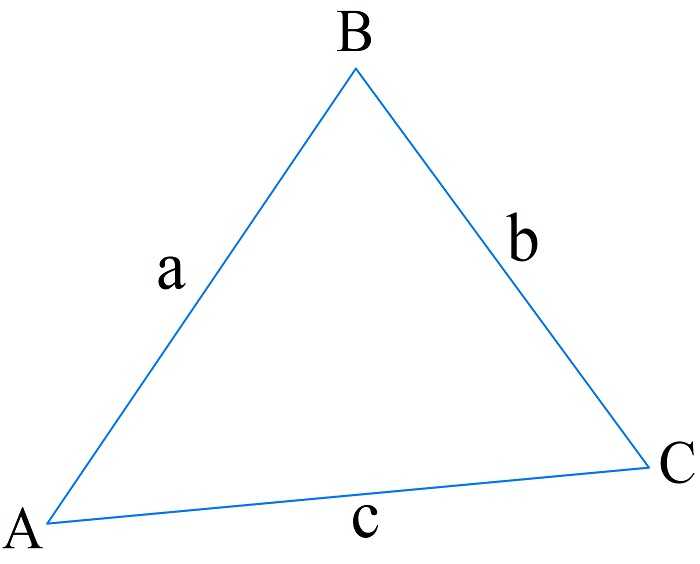
В этом случае необходимо знать длины всех ребер.
Формула 1
\(P=a+b+c\)
Вычисление периметра по средним линиям
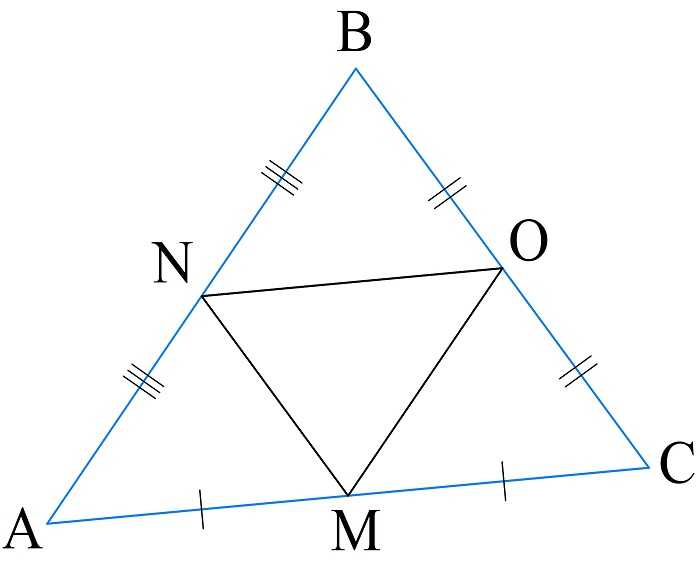
Средняя линия — линия, параллельная одной из сторон треугольника и равная половине ее длины. Значит, периметр треугольника, построенного по средним линиям данного, вдвое меньше периметра данного треугольника.
Формула 2
\(P_{\bigtriangleup ABC}=2\cdot P_{\bigtriangleup MNO}=2\cdot(MN+NO+OM)\)
Вычисление периметра по двум сторонам и углу между ними
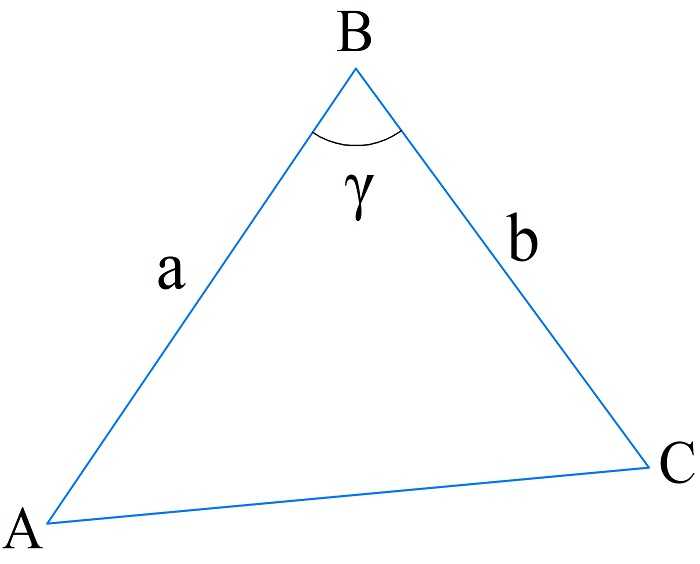
В этом случае известны только две стороны, а третью находят по теореме косинусов.
Тогда формулу для периметра можно записать в виде:
Формула 3
\(P_{\bigtriangleup ABC}=a+b+\sqrt{a^2+b^2-2ab\cdot\cos\gamma}\)
Вычисление периметра по радиусу вписанной окружности
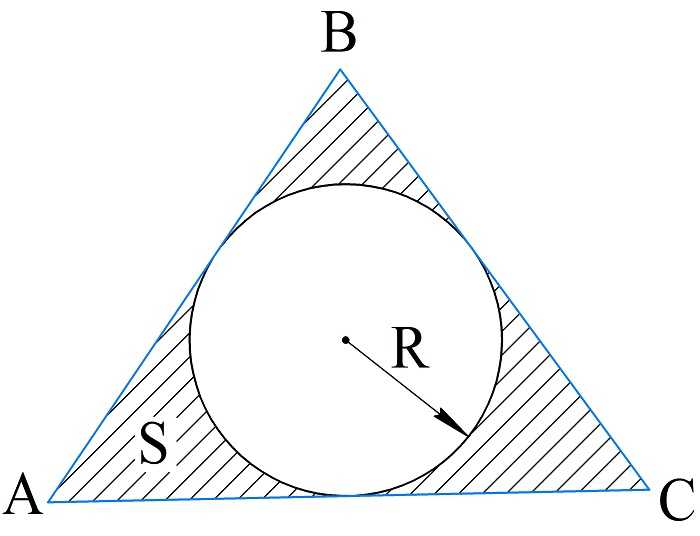
Согласно теореме о вписанной окружности в любой треугольник можно вписать окружность, именно поэтому этот способ применим для произвольных треугольников.
Итак, если известна площадь треугольника и радиус вписанной окружности, то периметр вычисляют по формуле:
Формула 4
\(P_{\bigtriangleup ABC}=\frac{2S_{\bigtriangleup ABC}}R\)
Вопрос-ответ:
Какие новые формулы будут на ОГЭ по математике в 2023 году?
Точный список формул еще не опубликован, но уже сейчас известно, что будет больше акцента на геометрии и решениях задач.
Как правильно решать задачи на геометрию на ОГЭ?
Для решения задач на геометрию нужно хорошо знать основные теоремы и определения, и уметь применять их в практике. Также необходимо уметь работать со схемами, рисунками, и находить соответствующие углы и стороны. Решая задачи на геометрию, также полезно использовать свои знания в алгебре для упрощения вычислений.
Как готовиться к ОГЭ по математике, если слабо знаком с геометрией?
Если вы слабо знакомы с геометрией, то необходимо уделить больше времени изучению этого раздела математики. Начинайте со знакомства с основными определениями и теоремами, а затем приступайте к решению задач. Не забывайте про отработку алгебраических навыков, которые помогут вам упростить вычисления. И, конечно, регулярное тренировочное применение теории на практике необходимо для того, чтобы закрепить материал.
8 способов найти периметр треугольника
Просто посчитайте сумму всех сторон.
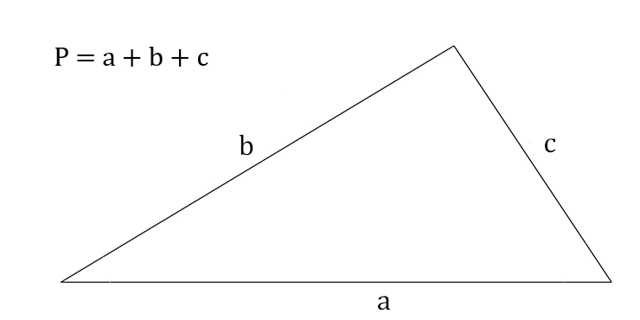Иллюстрация: Лайфхакер
- P — искомый периметр;
- a, b, c — стороны треугольника.
Сейчас читают ????
Загадка с подвохом: какая чашка наполнится кофе первой?
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
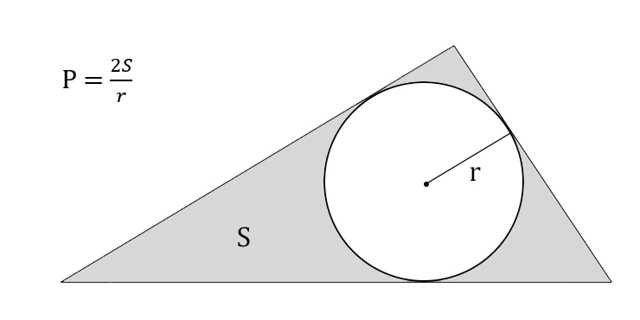Иллюстрация: Лайфхакер
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
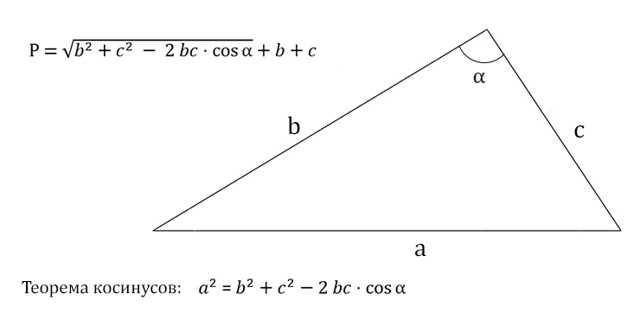Иллюстрация: Лайфхакер
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
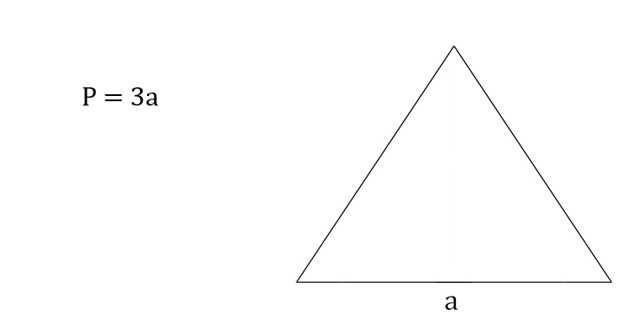Иллюстрация: Лайфхакер
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
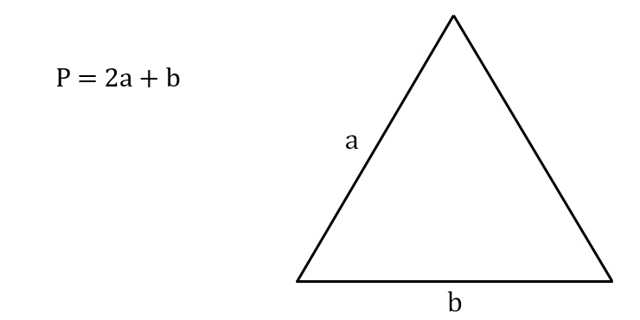Иллюстрация: Лайфхакер
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
- Найдите квадраты боковой стороны и высоты.
- Отнимите от первого числа второе.
- Найдите корень из результата и умножьте его на 2.
- Прибавьте к полученному числу две боковые стороны.
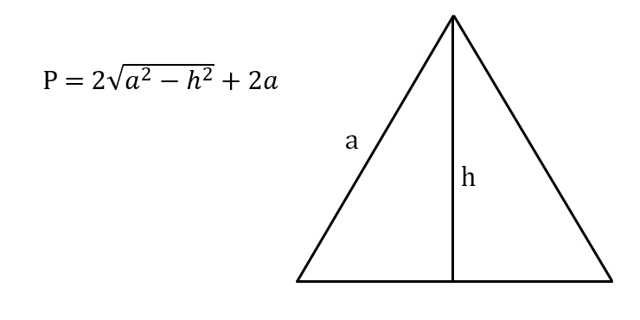Иллюстрация: Лайфхакер
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
- Найдите квадраты катетов и посчитайте их сумму.
- Извлеките корень из полученного числа.
- Прибавьте к результату оба катета.
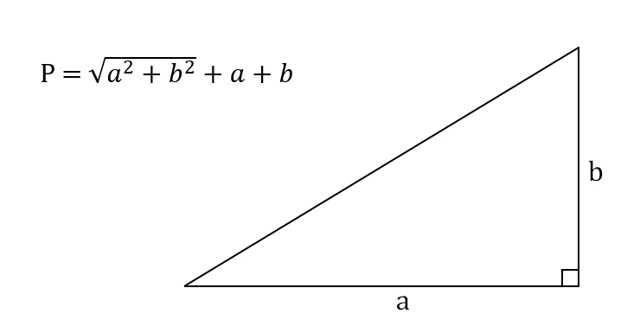Иллюстрация: Лайфхакер
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
- Посчитайте квадраты гипотенузы и катета.
- Отнимите от первого числа второе.
- Найдите корень из результата.
- Прибавьте катет и гипотенузу.
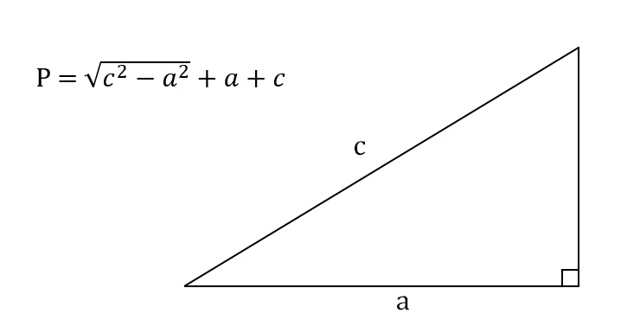Иллюстрация: Лайфхакер
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+β+γ$
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
Решение.
По рассмотренному выше примеру, видим, что
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Решение.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α^2=6^2+8^2$
$α^2=100$
$α=10$По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
В статье на примерах покажем, как находить периметр треугольника
. Рассмотрим все основные случая, как найти периметры треугольников
, даже когда не все значения сторон известны.
Треугольником
называется простая геометрическая фигура состоящая из трех прямых линий пересекающих друг друга. В которой точки пересечения прямых, называются вершинами, а прямые линии соединяющие их, называются сторонами.Периметром треугольника
называется сумма длин сторон треугольника. От того сколько мы имеем изначальных данных, для вычисления периметра треугольника, зависит каким из вариантов мы воспользуемся, для его вычисления.
Первый вариант
Если мы знаем длины сторон n, y и z треугольника, то периметр мы можем определить с помощью следующей формулы: в которой P — это периметр, n, y, z- стороны треугольника
периметр прямоугольника формула
P = n + y + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =8см. найти его периметр.
Пользуясь формулой получаем 10 + 10 + 8 = 28.
Ответ: Р = 28см.
Для равностороннего треугольника находим периметр так — длина одной стороны умноженная на три. формула выглядит следующим образом:
Р = 3n
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =10см. найти его периметр.
Пользуясь формулой получаем 10 * 3 = 30
Ответ: Р = 30см.
Для равнобедренного треугольника находим периметр так — к длине одной боковой стороны умноженной на два, прибавляем сторону основания
Равнобедренным треугольником называется простейший многоугольник у которого две боковые стороны равны, а третья сторона называется основанием.
P = 2n + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =7см. найти его периметр.
Пользуясь формулой получаем 2 * 10 + 7 = 27.
Ответ: Р = 27см.
Второй вариант
Когда нам не известна длина одной стороны, но мы знаем величины длины двух других сторон и угла между ними, а периметр треугольника возможно найти только после того как мы узнаем длину третьей стороны. В этом случае неизвестная сторона будет равна корню квадратному из выражения в2 + с2 — 2 ∙ в ∙ с ∙ cosβ
P = n + y + √ (n2 + y2 — 2 ∙ n ∙ y ∙ cos α)
n, y — длины сторон
α — размер угла между известными нам сторонами
Третий вариант
Когда нам не известны стороны n и y, но мы знаем длину стороны z и величины прилегающих к ней. Периметр треугольника в этом случае мы сможем найти только тогда когда узнаем длины двух неизвестных нам сторон, определим их с помощью теоремы синусов, с помощью формулы
P = z + sinα ∙ z / (sin (180°-α — β)) + sinβ ∙ z / (sin (180°-α — β))
z — длина известной нам стороны
α, β — размеры известных нам углов
Четвертый вариант
Так же можно найти периметр треугольника по радиусу вписанному в его окружность и площади треугольника. Определяем периметр по формуле
P = 2S / r
S — площадь треугольника
r — радиус вписанной в него окружности
Кстати, на referatplus.ru вы можете скачать рефераты по математике бесплатно .
Решение задач на поиск углов, высот и медиан
Поиск углов
Для решения задач на поиск углов необходимо использовать знания о свойствах геометрических фигур. Например, в треугольнике сумма углов равна 180 градусов. Если известны два угла, третий можно найти как разность 180 и суммы известных углов. Если известны длины сторон треугольника, можно воспользоваться теоремой косинусов или теоремой синусов для нахождения углов.
Поиск высоты
Чтобы найти высоту треугольника, нужно провести перпендикуляр от точки пересечения высот к противоположной стороне. Также можно воспользоваться формулой для нахождения площади треугольника через стороны и используемую сторону высотой.
Поиск медианы
Медиана — это линия, которая проходит через вершину треугольника и середину противолежащей стороны. Для нахождения медианы нужно провести линию из вершины к середине противолежащей стороны. Нахождение медианы также может осуществляться через теорему Пифагора, если известны длины сторон треугольника.
Способы нахождения
По трем сторонам
Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:
\(P = a+b+c\)
где a, b и с — это стороны треугольника.
В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:
\(P=a+2b\) или \(P=a+2c \)
где a — основание фигуры, а b и с — равные ребра.
Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:
\(P=3a\)
где a — это любая сторона фигуры.
По площади и радиусу вписанной окружности
Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:
\(P=\frac{2S}r\)
где S — площадь фигуры, r — радиус вписанной в нее окружности.
По двум сторонам и углу между ними
Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.
Теорема косинусов выглядит так:
\(a^2=b^2+c^2-2bc\times\cos\alpha\)
где α — известный угол.
Тогда формула для расчета периметра всей фигуры в этом случае:
\(P=\sqrt{b^2+c^2-2bc\times\cos\alpha}+b+c\)
По боковой стороне и высоте (для равнобедренного)
Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.
Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:
\(d^2=a^2-h^2\)
\(d=\sqrt{a^2-h^2}\)
где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.
Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.
\(P=2\sqrt{a^2-h^2}+2a\)
По двум катетам (для прямоугольного)
Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).
\(c^2=a^2+b^2\)
\(c=\sqrt{a^2+b^2}\)
где a и b — катеты треугольника.
Подставляем значение c в формулу для нахождения периметра и получаем:
\(P=\sqrt{a^2+b^2}+a+b\)
Знакомство с геометрией ОГЭ
Что такое геометрия в ОГЭ?
Геометрия – это одна из трех разделов математики, изучаемых на ОГЭ. Она изучает пространственные фигуры и их свойства. В ОГЭ геометрия представлена задачами на построение геометрических фигур, вычислениях и решении уравнений.
Как готовиться к геометрии на ОГЭ?
Для подготовки к геометрии на ОГЭ необходимо пройтись по основным темам, изучаемым в геометрии, и необходимо понимать, как решать задачи на их основе.
Основные темы в геометрии, изучаемые на ОГЭ:
- Круг и его элементы (длина окружности, площадь круга, соотношение между длиной окружности и диаметром)
- Треугольник (основные свойства, методы нахождения типов треугольников, теоремы Пифагора и косинусов)
- Прямоугольник, квадрат (основные свойства, площадь и периметр)
- Трапеция и параллелограмм (основные свойства, площадь)
Необходимо уметь строить и читать геометрические фигуры, а также использовать полученные знания для решения задач на геометрию.
Важно также понимать, какими формулами и методами решения следует пользоваться в данной задаче на геометрию
Стоит обратить внимание на то, что на ОГЭ большое внимание уделяется практическому применению знаний, поэтому необходимо уметь применять геометрические методы для решения бытовых задач
Второй метод: прямоугольный треугольник и две известные его стороны
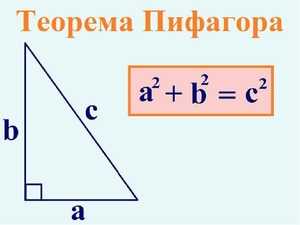В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.
Описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:
-
Гипотенуза
. Она всегда расположена противоположно прямому углу (90 градусов), а также является самой длинной гранью треугольника. В математике принято обозначать гипотенузу буквой c. -
Катеты
— это грани прямоугольного треугольника, которые относятся к прямому углу и обозначаются буквами а и b. Один из катетов одновременно является и высотой фигуры.
Таким образом, если условиями задачи заданы длины двух из трех граней такой геометрической фигуры, с помощью теоремы Пифагора необходима найти размерность третьей грани, после чего воспользоваться формулой из первого метода.
Например, мы знаем длину 2-х катетов: a = 3 см, b = 5 см. Подставляем значения в теорему: 3^2 + 4^2 = c^2 => 9 + 16 = c^2 => 25 = c^2 => c = 5 см. Итак, гипотенуза такого треугольника равна 5 см. К слову, данный пример является самым распространенным и называется . Иными словами, если два катета фигуры равны 3 см и 4 см, то гипотенуза составит 5 см соответственно.
Если неизвестна длина одного из катетов, необходимо преобразовать формулу следующим образом: c^2 — a^2 = b^2. И наоборот для другого катета.
Продолжим пример. Теперь необходимо обратиться к стандартной формуле поиска периметра фигуры: P = a + b + c. В нашем случае: P = 3 + 4 + 5 = 12 см.
Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.