Калькулятор и таблица тангенса и котангенса

Таблица тангенсов от 0° до 180°


tg (0°)
tg (1°)	0,017455	tg (61°)	1,804048	tg (121°)	-1,664279
tg (2°)	0,034921	tg (62°)	1,880726	tg (122°)	-1,600335
tg (3°)	0,052408	tg (63°)	1,962611	tg (123°)	-1,539865
tg (4°)	0,069927	tg (64°)	2,050304	tg (124°)	-1,482561
tg (5°)	0,087489	tg (65°)	2,144507	tg (125°)	-1,428148
tg (6°)	0,105104	tg (66°)	2,246037	tg (126°)	-1,376382
tg (7°)	0,122785	tg (67°)	2,355852	tg (127°)	-1,327045
tg (8°)	0,140541	tg (68°)	2,475087	tg (128°)	-1,279942
tg (9°)	0,158384	tg (69°)	2,605089	tg (129°)	-1,234897
tg (10°)	0,176327	tg (70°)	2,747477	tg (130°)	-1,191754
tg (11°)	0,19438	tg (71°)	2,904211	tg (131°)	-1,150368
tg (12°)	0,212557	tg (72°)	3,077684	tg (132°)	-1,110613
tg (13°)	0,230868	tg (73°)	3,270853	tg (133°)	-1,072369
tg (14°)	0,249328	tg (74°)	3,487414	tg (134°)	-1,03553
tg (15°)	0,267949	tg (75°)	3,732051	tg (135°)	-1
tg (16°)	0,286745	tg (76°)	4,010781	tg (136°)	-0,965689
tg (17°)	0,305731	tg (77°)	4,331476	tg (137°)	-0,932515
tg (18°)	0,32492	tg (78°)	4,70463	tg (138°)	-0,900404
tg (19°)	0,344328	tg (79°)	5,144554	tg (139°)	-0,869287
tg (20°)	0,36397	tg (80°)	5,671282	tg (140°)	-0,8391
tg (21°)	0,383864	tg (81°)	6,313752	tg (141°)	-0,809784
tg (22°)	0,404026	tg (82°)	7,11537	tg (142°)	-0,781286
tg (23°)	0,424475	tg (83°)	8,144346	tg (143°)	-0,753554
tg (24°)	0,445229	tg (84°)	9,514364	tg (144°)	-0,726543
tg (25°)	0,466308	tg (85°)	11,430052	tg (145°)	-0,700208
tg (26°)	0,487733	tg (86°)	14,300666	tg (146°)	-0,674509
tg (27°)	0,509525	tg (87°)	19,081137	tg (147°)	-0,649408
tg (28°)	0,531709	tg (88°)	28,636253	tg (148°)	-0,624869
tg (29°)	0,554309	tg (89°)	57,289962	tg (149°)	-0,600861
tg (30°)	0,57735	tg (90°)	∞	tg (150°)	-0,57735
tg (31°)	0,600861	tg (91°)	-57,289962	tg (151°)	-0,554309
tg (32°)	0,624869	tg (92°)	-28,636253	tg (152°)	-0,531709
tg (33°)	0,649408	tg (93°)	-19,081137	tg (153°)	-0,509525
tg (34°)	0,674509	tg (94°)	-14,300666	tg (154°)	-0,487733
tg (35°)	0,700208	tg (95°)	-11,430052	tg (155°)	-0,466308
tg (36°)	0,726543	tg (96°)	-9,514364	tg (156°)	-0,445229
tg (37°)	0,753554	tg (97°)	-8,144346	tg (157°)	-0,424475
tg (38°)	0,781286	tg (98°)	-7,11537	tg (158°)	-0,404026
tg (39°)	0,809784	tg (99°)	-6,313752	tg (159°)	-0,383864
tg (40°)	0,8391	tg (100°)	-5,671282	tg (160°)	-0,36397
tg (41°)	0,869287	tg (101°)	-5,144554	tg (161°)	-0,344328
tg (42°)	0,900404	tg (102°)	-4,70463	tg (162°)	-0,32492
tg (43°)	0,932515	tg (103°)	-4,331476	tg (163°)	-0,305731
tg (44°)	0,965689	tg (104°)	-4,010781	tg (164°)	-0,286745
tg (45°)	1	tg (105°)	-3,732051	tg (165°)	-0,267949
tg (46°)	1,03553	tg (106°)	-3,487414	tg (166°)	-0,249328
tg (47°)	1,072369	tg (107°)	-3,270853	tg (167°)	-0,230868
tg (48°)	1,110613	tg (108°)	-3,077684	tg (168°)	-0,212557
tg (49°)	1,150368	tg (109°)	-2,904211	tg (169°)	-0,19438
tg (50°)	1,191754	tg (110°)	-2,747477	tg (170°)	-0,176327
tg (51°)	1,234897	tg (111°)	-2,605089	tg (171°)	-0,158384
tg (52°)	1,279942	tg (112°)	-2,475087	tg (172°)	-0,140541
tg (53°)	1,327045	tg (113°)	-2,355852	tg (173°)	-0,122785
tg (54°)	1,376382	tg (114°)	-2,246037	tg (174°)	-0,105104
tg (55°)	1,428148	tg (115°)	-2,144507	tg (175°)	-0,087489
tg (56°)	1,482561	tg (116°)	-2,050304	tg (176°)	-0,069927
tg (57°)	1,539865	tg (117°)	-1,962611	tg (177°)	-0,052408
tg (58°)	1,600335	tg (118°)	-1,880726	tg (178°)	-0,034921
tg (59°)	1,664279	tg (119°)	-1,804048	tg (179°)	-0,017455
tg (60°)	1,732051	tg (120°)	-1,732051	tg (180°)

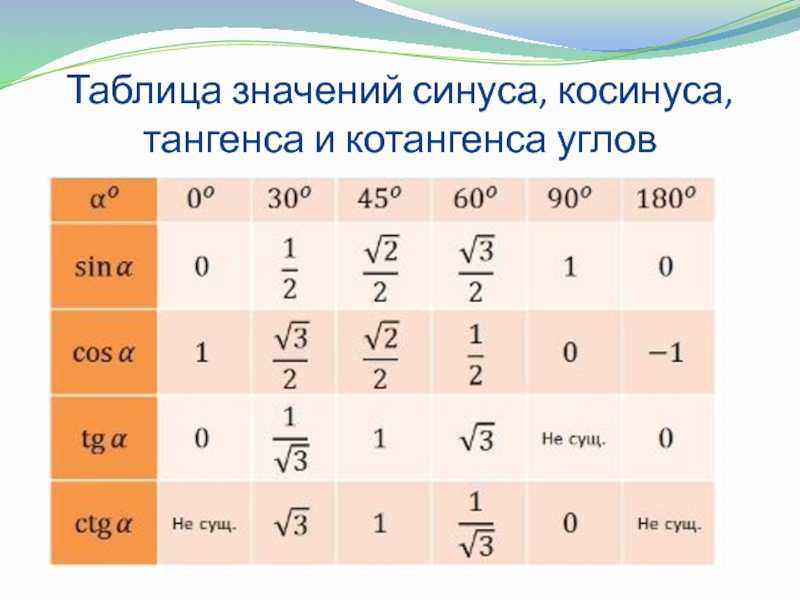
Быстрые приемы запоминания тригонометрических таблиц

В дополнение к описанным выше методам есть еще один метод, который вы можете использовать, чтобы легко запомнить таблицы тригонометрических формул.

Вам нужно сделать следующие шаги:

Шаг 1 . Создайте таблицу, содержащую углы от 0 до 90 градусов и столбцы с описанием sin cos tan

Шаг 2

Обратите внимание, что общая формула для sin в диапазоне от 0 до 90 градусов равна √x / 2.

Шаг 3. Измените значение x на 0 на √x / 2 в самом первом столбце

Верхний левый угол.

Шаг 4. Заполните последовательность, изменив x на 0, 1, 2, 3, 4 в столбце sin. Таким образом, вы получили полное тригонометрическое значение sin

Шаг 5 . Чтобы найти значение cos, все, что вам нужно сделать, это изменить порядок в столбце sin.

Шаг 6 . Чтобы найти значение tan, все, что вам нужно сделать, это разделить значение sin на значение cos.

Какой из них вам легче понять, чтобы запомнить триггерное значение tan sin cos?

В любом случае выберите тот, который вам легче всего понять. Потому что у каждого человека свой стиль обучения.

Тригонометрические функции произвольного угла

Что такое угол и угловой градус, мы предполагаем известными читателю из курса геометрии.

.В теории тригонометрических функций угол рассматривается как величина, могущая принимать любые положительные и отрицательные значения, а также и значение, равное нулю.

Например, если луч OA (или вектор ), оставаясь в данной плоскости, совершит 10 полных оборотов вокруг точки О против движения часовой стрелки и еще ‘ повернется в том же направлении на угол 120°, то говорят, что этим движением луча OA образован угол, содержащий 360° • 10 + 120°, т. е. 3720°.

Допустим, что на рисунке 153 луч ОМ (или вектор ) изображает положение луча OA после указанного выше его вращения вокруг точки О. Тогда мы скажем что луч ОМ составляет с лучом (или вектор с вектором ) угол, содержащий 3720°.

Вращение луча OA в данной плоскости вокруг точки О может происходить в двух противоположных направлениях (против движения часовой стрелки и по ее движению).

Поэтому величину угла, полученного при вращении против движения часовой стрелки, принято выражать положительным числом, а образованного вращением по движению часовой стрелки — отрицательным числом.

Например, если луч совершит 10 полных оборотов по движению часовой стрелки и повернется в том же направлении еще на 120°, то мы скажем, что этим движением образован угол, равный — 3720° (минус 3720°).

Если луч совершит один полный оборот против движения часовой стрелки, то его положение совпадет с первоначальным, а угол, образованный этим движением, будет равен 360°. Если бы такое же вращение произошло по движению часовой стрелки, то угол был бы равен —360°.

Если луч совершит пол-оборота против движения часовой стрелки, то он займет положение, противоположное первоначальному, а угол, образованный этим движением, будет равен 180°. Если бы такое же вращение произошло по движению часовой стрелки, то угол был бы равен — 180°.

Если луч не совершив никакого движения, находится в положении, совпадающем с лучом то и в этом случае принято считать, что совпадающие лучи и также составляют угол, причем такой угол считается равным нулю.

Углы, по абсолютной величине большие 360°, мы можем наблюдать, например, при завертывании или отвертывании гайки ключом, при вращении воздушного винта и т. п.

Угол, описанный минутной стрелкой часов за 6,25 часа, содержит — 360° • 6 + (— 90°), т. е. — 2250°. Секундная же стрелка за это время опишет угол— 135000°.

Таблицы тригонометрических функций

Из тригонометрических определений функций $sin$, $cos$, $ an$ и $cot$ можно узнать их значения для углов $0$ и $90$ градусов:
$sin⁡0°=0$, $cos0°=1$, $ an 0°=0$, $cot 0°$ не определяется;
$sin90°=1$, $cos90°=0$, $cot90°=0$, $ an 90°$ не определяется.
В школьном курсе геометрии при изучении прямоугольных треугольников находят тригонометрические функции углов $0°$, $30°$, $45°$, $60°$ и $90°$.

Найденные значения тригонометрических функций для указанных углов в градусах и радианах соответственно ($0$, $frac{pi}{6}$, $frac{pi}{4}$, $frac{pi}{3}$, $frac{pi}{2}$) для удобства запоминания и использования заносят в таблицу, которую называют тригонометрической таблицей, таблицей основных значений тригонометрических функций и т.п.

При использовании формул приведения, тригонометрическая таблица может быть расширена до угла $360°$ и соответственно $2pi$ радиан:

Применяя свойства периодичности тригонометрических функций, каждый угол, который будет отличаться от уже известного на $360°$, можно рассчитать и записать в таблицу. Например, тригонометрическая функция для угла $0°$ будет иметь такое же значение и для угла $0°+360°$, и для угла $0°+2 cdot 360°$, и для угла $0°+3 cdot 360°$ и т.д.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

С помощью тригонометрической таблицы можно определить значения всех углов единичной окружности.

В школьном курсе геометрии предполагается запоминание основных значений тригонометрических функций, собранных в тригонометрической таблице, для удобства решения тригонометрических задач.

Использование таблицы

В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $cos⁡60°$, которое равно $frac{1}{2}$.

Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $ an 1 380°= an (1 380°-360°)= an(1 020°-360°)= an(660°-360°)= an300°$:

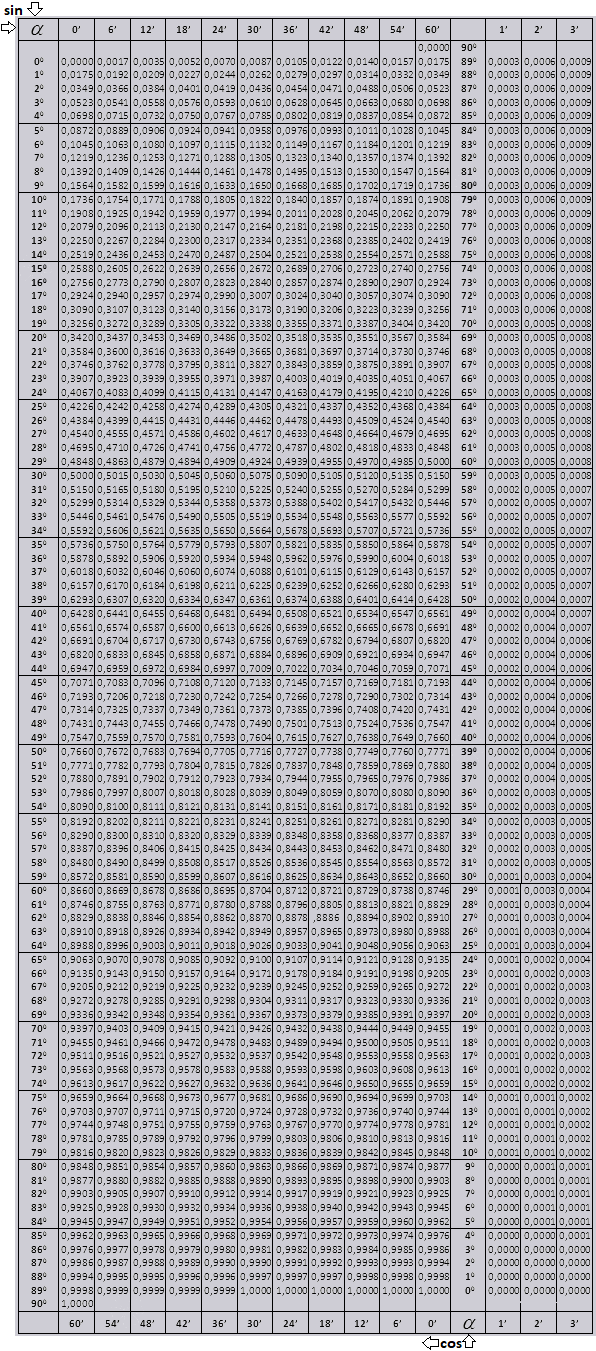
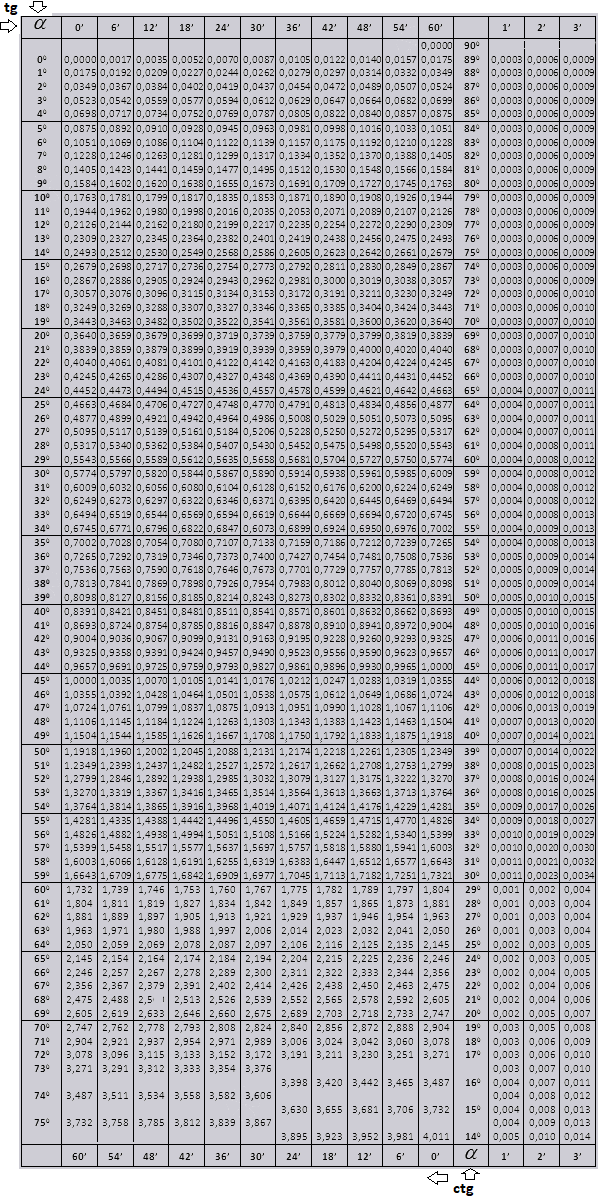
Таблицы Брадиса основных тригонометрических функций

Возможность расчета тригонометрической функции абсолютно любого значения угла для целого значения градусов и целого значения минут дает использование таблиц Брадиса. Например, найти значение $cos⁡34°7’$. Таблицы разделены на 2 части: таблицу значений $sin$ и $cos$ и таблицу значений $ an$ и $cot$.

Таблицы Брадиса дают возможность получить приближенное значение тригонометрических функций с точностью до 4-х знаков после десятичной запятой.

Использование таблиц Брадиса

Используя таблицы Брадиса для синусов, найдем $sin⁡17°42’$. Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42’$. На их пересечении получаем искомое значение:

$sin17°42’=0,304$.

Для нахождения значения $sin17°44’$ нужно воспользоваться поправкой в правой части таблицы. В данном случае к значению $42’$, которое есть в таблице, нужно добавить поправку для $2’$, которая равна $0,0006$. Получим:

$sin17°44’=0,304+0,0006=0,3046$.

Для нахождения значения $sin17°47’$ также пользуемся поправкой в правой части таблицы, только в этом случае за основу берем значение $sin17°48’$ и отнимаем поправку для $1’$:

$sin17°47’=0,3057-0,0003=0,3054$.

При расчете косинусов выполняем аналогичные действия, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, $cos20°=0,9397$.

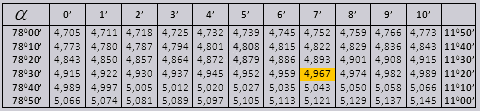
Для значений тангенса до $90°$ и котангенса малого угла поправок нет. Например, найдем $ an 78°37’$, который по таблице равен $4,967$.

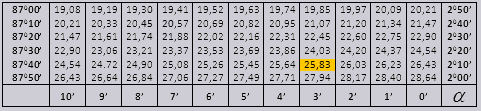
Найдем $cot 2°13’=25,83$.

Таблица синусов, косинусов, тангенсов и котангенсов!

Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:

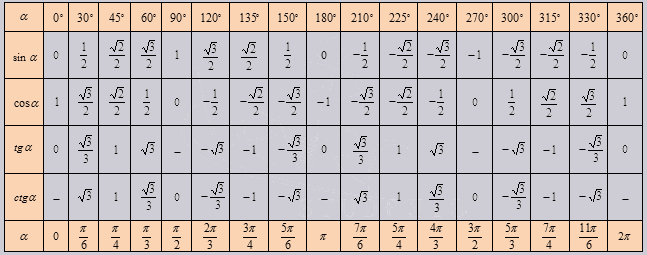
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.

Разберем наглядно как использовать таблицу в решении. Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:

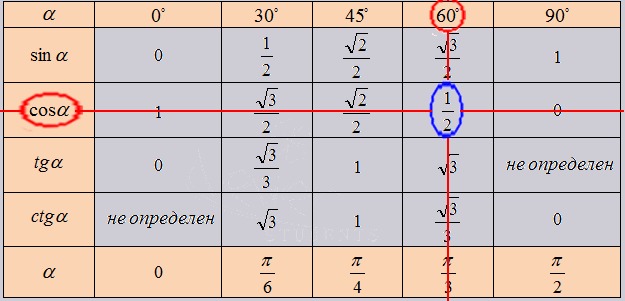
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 10200 = 3000+3600*2. Найдем по таблице.

Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.

Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).

Синус и косинус

tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.

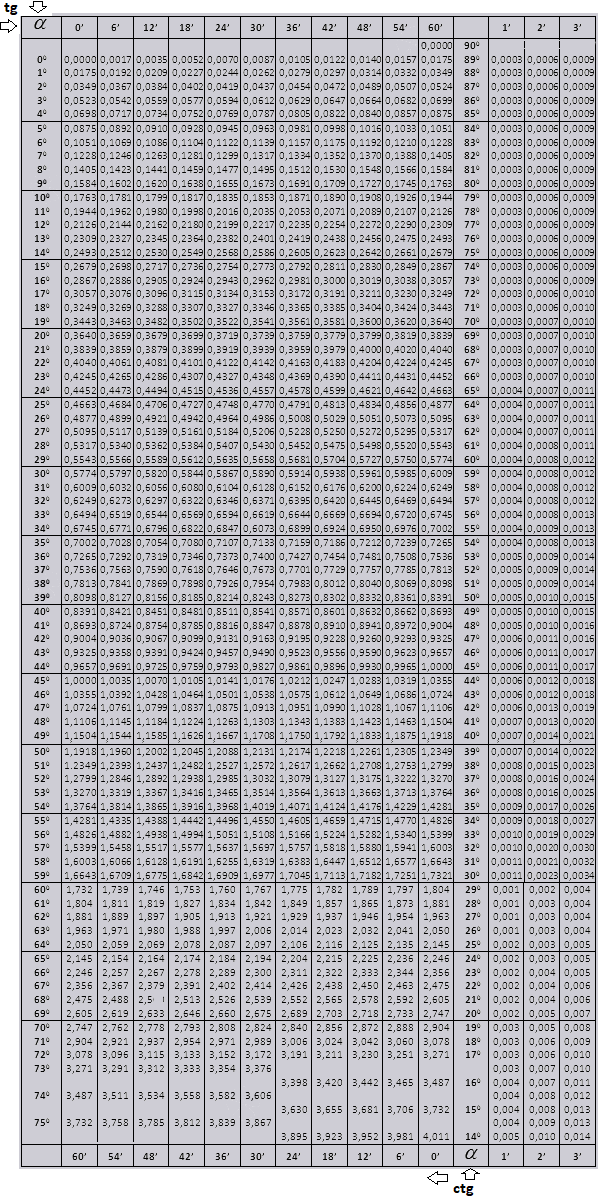
tg до 900 и ctg малых углов.

Разберемся как пользоваться таблицами Брадиса в решении задач.

Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.

Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т. е 0,3057 — 0,0003 = 0,3054

При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0. 9397

Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 780 37мин = 4,967

а ctg 200 13мин = 25,83

Тригонометрия — это раздел математики, в котором рассматриваются стороны и углы треугольников. Зачастую в тригонометрических задачах нужно найти значения тригонометрических функций, а именно синус, косинус и тангенс угла треугольника. С помощью специальной таблицы или прямоугольного треугольника можно быстро вычислить значения тригонометрических функций наиболее распространенных углов.

Если в задаче нужно вычислить синус, косинус или тангенс угла, скорее всего, стороны прямоугольного треугольника будут даны.
Синус угла равен отношению противолежащего катета к гипотенузе.Косинус угла равен отношению прилежащего катета к гипотенузе.Тангенс угла равен отношению противолежащего катета к прилежащему.Например, чтобы вычислить sin 35°, разделите длину противолежащего катета на гипотенузу. Если противолежащий катет равен 2,8, а гипотенуза равна 4,9, sin 35° = 2,8/4,9 = 0,57.
Синус угла равен отношению противолежащего катета к гипотенузе.
Косинус угла равен отношению прилежащего катета к гипотенузе.
Тангенс угла равен отношению противолежащего катета к прилежащему.
Например, чтобы вычислить sin 35°, разделите длину противолежащего катета на гипотенузу. Если противолежащий катет равен 2,8, а гипотенуза равна 4,9, sin 35° = 2,8/4,9 = 0,57.
Еще раз запомните: sin = (противолежащий катет)/гипотенуза; cos = (прилежащий катет)/гипотенуза; tg = (противолежащий катет)/(прилежащий катет).
cosec = 1/sin, поэтому косеканс равен отношению гипотенузы к противолежащему катету.sec = 1/cos, поэтому секанс равен отношению гипотенузы к прилежащему катету.ctg = 1/tg, поэтому котангенс равен отношению прилежащего катета к противолежащему.Например, чтобы вычислить cosec 35°, если противолежащий катет равен 2,8, а гипотенуза равна 4,9, разделите 4,9 на 2,8 и получите cosec 35° = 1,75.
cosec = 1/sin, поэтому косеканс равен отношению гипотенузы к противолежащему катету.
sec = 1/cos, поэтому секанс равен отношению гипотенузы к прилежащему катету.
ctg = 1/tg, поэтому котангенс равен отношению прилежащего катета к противолежащему.
Например, чтобы вычислить cosec 35°, если противолежащий катет равен 2,8, а гипотенуза равна 4,9, разделите 4,9 на 2,8 и получите cosec 35° = 1,75.

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный.

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin2α + cos2α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.

sin2α + cos2α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin2α + cos2α = 1

Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
Если развернуть точку A на угол α, то точка A становится на место точки A₁.
По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A₁ получает координаты cos α, sin α.
Опускаем перпендикулярную прямую A₁B на x0 из точки A₁.
Образовался прямоугольный треугольник OA₁B.
|A₁B| = |у|
|OB| = |x|.
Гипотенуза OA₁ имеет значение, равное радиусу единичной окружности.
|OA₁| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A₁B|2 + |OB|2 = |OA₁|2.
Записываем в виде: |y|2 + |x|2 = 12.
Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:
OB = cos α
A₁B = sin α
A₁O = 1
Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

sin α = ±
cos α = ±

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Пройти урок

Редакции и ведущие

TG1 руда 16:30 / Economia

С понедельника по воскресенье с 16:30 до 17:00 (3–11 минут) Докладчики:

Барбара Каппони
Марина Налессо
Франческа Гримальди

ТГ1 руда 20:00

С понедельника по воскресенье в 20:00 (30–36 минут). Ведущие:

Франческо Джорджино
Эмма Д’Акино
Лаура Чименти
Алессио Цуккини

TG1 60 секунд / TG1 Notte

С понедельника по воскресенье примерно в 23:00 (1 минута), а TG1 Notte выходит в эфир с 00:00 до 01:00 (30 минут). Ведущие:

Барбара Карфанья
Габриэлла Каппарелли
Алессандра Ди Томмазо
Сесилия Примерано
Паола Сервелли
Перла Дипоппа
Джанпьеро Скарпати
Роберто Чинзари

Speciale Tg1

Он выходит в эфир только в воскресенье, около 23:00. За этим шоу ухаживает Амедо Марторелли. Координационное издание представили Серджио Фратини и Массимо Пройетти.

Таблица значений sin а с точностью до 0,001 для углов от 1 до 89°

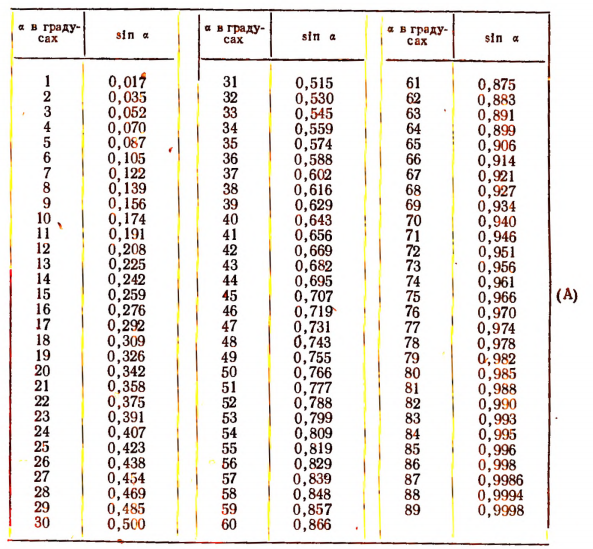
Таблицу (А) нужно читать и понимать так: если угол возрастает от 0 до 90°, то sin возрастает от 0 до 1; если угол возрастает от 90 до 180°, то sin убывает от 1 до 0 и т. д. Если угол станет возрастать от 360 до 450°, то sin снова станет возрастать от О до 1, т. е. процесс изменения sin станет повторяться после каждого полного оборота радиуса-вектора . Поэтому

sin (360° n + а) = sin а,

где n — любое целое число (положительное, отрицательное или нуль).

Обратим внимание на то, что

Каждому значению соответствует единственное определенное значение sin , т. е. sin есть однозначная функция аргумента .

Значения функции sin а суть числа отвлеченные.

С изменением угла изменяется и sin . Однако могут быть случаи, когда неодинаковые углы имеют одинаковые синусы. Например,

Синус по своему абсолютному значению никогда не может быть больше единицы, т. е.

Примечание:

Символ sin не является синусом, а является лишь знаком синуса. Выражение же sin уже является синусом, а именно синусом угла .

Синус острого угла. В прямоугольном треугольнике ОМР (рис. 158) с острым углом отрезок MP есть катет, противолежащий углу , а отрезок ОМ есть гипотенуза. Поэтому синус острого угла прямоугольного треугольника есть отношение катета, противолежащего углу , к гипотенузе.

Пусть в прямоугольном треугольнике катеты равны а и b, гипотенуза равна с и острые углы обозначены и (рис. 159). Тогда

Задача:

Найти сторону вписанного в круг правильного девятиугольника по данному радиусу круга.

Пусть радиус круга равен r, а хорда АВ есть сторона правильного девятиугольника. Пусть (рис. 160). Тогда

Из прямоугольного треугольника АОС следует, что sin 20° = Отсюда

С грубым приближением сторона правильного вписанного в круг девятиугольника равна .

Графики тригонометрических функций. Тангенс, котангенс

График функции y=tgx

Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .
Надеюсь, вы помните, где располагается ось тангенсов…

Переносим основные значения углов, представленные на круге, например, из I и IV четвертей и соответствующие им значения тангенса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения тангенса угла.

Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на .

Обратите внимание! Тангенс в точках не существует. Мы лишь можем сколь угодно близко «подбираться» к этим значениям

Указанный выше фрагмент графика тангенса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
График функции является симметричным относительно начала координат.

График функции y=ctgx

Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и .
Поступим несколько иначе.
Согласно формулам приведения или, что тоже самое, что .

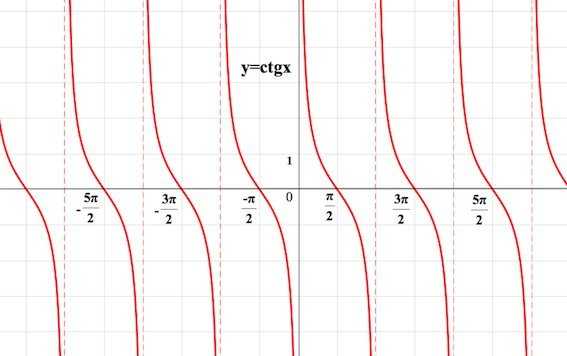
График функции является симметричным относительно начала координат.

Таблица тангенсов углов от 181° до 360°

tg(181°) = 0.01746tg(182°) = 0.03492tg(183°) = 0.05241tg(184°) = 0.06993tg(185°) = 0.08749tg(186°) = 0.1051tg(187°) = 0.12278tg(188°) = 0.14054tg(189°) = 0.15838tg(190°) = 0.17633tg(191°) = 0.19438tg(192°) = 0.21256tg(193°) = 0.23087tg(194°) = 0.24933tg(195°) = 0.26795tg(196°) = 0.28675tg(197°) = 0.30573tg(198°) = 0.32492tg(199°) = 0.34433tg(200°) = 0.36397tg(201°) = 0.38386tg(202°) = 0.40403tg(203°) = 0.42447tg(204°) = 0.44523tg(205°) = 0.46631tg(206°) = 0.48773tg(207°) = 0.50953tg(208°) = 0.53171tg(209°) = 0.55431tg(210°) = 0.57735tg(211°) = 0.60086tg(212°) = 0.62487tg(213°) = 0.64941tg(214°) = 0.67451tg(215°) = 0.70021tg(216°) = 0.72654tg(217°) = 0.75355tg(218°) = 0.78129tg(219°) = 0.80978tg(220°) = 0.8391tg(221°) = 0.86929tg(222°) = 0.9004tg(223°) = 0.93252tg(224°) = 0.96569tg(225°) = 1tg(226°) = 1.03553tg(227°) = 1.07237tg(228°) = 1.11061tg(229°) = 1.15037tg(230°) = 1.19175tg(231°) = 1.2349tg(232°) = 1.27994tg(233°) = 1.32704tg(234°) = 1.37638tg(235°) = 1.42815tg(236°) = 1.48256tg(237°) = 1.53986tg(238°) = 1.60033tg(239°) = 1.66428tg(240°) = 1.73205

tg(241°) = 1.80405tg(242°) = 1.88073tg(243°) = 1.96261tg(244°) = 2.0503tg(245°) = 2.14451tg(246°) = 2.24604tg(247°) = 2.35585tg(248°) = 2.47509tg(249°) = 2.60509tg(250°) = 2.74748tg(251°) = 2.90421tg(252°) = 3.07768tg(253°) = 3.27085tg(254°) = 3.48741tg(255°) = 3.73205tg(256°) = 4.01078tg(257°) = 4.33148tg(258°) = 4.70463tg(259°) = 5.14455tg(260°) = 5.67128tg(261°) = 6.31375tg(262°) = 7.11537tg(263°) = 8.14435tg(264°) = 9.51436tg(265°) = 11.43005tg(266°) = 14.30067tg(267°) = 19.08114tg(268°) = 28.63625tg(269°) = 57.28996tg(270°) = ∞tg(271°) = -57.28996tg(272°) = -28.63625tg(273°) = -19.08114tg(274°) = -14.30067tg(275°) = -11.43005tg(276°) = -9.51436tg(277°) = -8.14435tg(278°) = -7.11537tg(279°) = -6.31375tg(280°) = -5.67128tg(281°) = -5.14455tg(282°) = -4.70463tg(283°) = -4.33148tg(284°) = -4.01078tg(285°) = -3.73205tg(286°) = -3.48741tg(287°) = -3.27085tg(288°) = -3.07768tg(289°) = -2.90421tg(290°) = -2.74748tg(291°) = -2.60509tg(292°) = -2.47509tg(293°) = -2.35585tg(294°) = -2.24604tg(295°) = -2.14451tg(296°) = -2.0503tg(297°) = -1.96261tg(298°) = -1.88073tg(299°) = -1.80405tg(300°) = -1.73205

tg(301°) = -1.66428tg(302°) = -1.60033tg(303°) = -1.53986tg(304°) = -1.48256tg(305°) = -1.42815tg(306°) = -1.37638tg(307°) = -1.32704tg(308°) = -1.27994tg(309°) = -1.2349tg(310°) = -1.19175tg(311°) = -1.15037tg(312°) = -1.11061tg(313°) = -1.07237tg(314°) = -1.03553tg(315°) = -1tg(316°) = -0.96569tg(317°) = -0.93252tg(318°) = -0.9004tg(319°) = -0.86929tg(320°) = -0.8391tg(321°) = -0.80978tg(322°) = -0.78129tg(323°) = -0.75355tg(324°) = -0.72654tg(325°) = -0.70021tg(326°) = -0.67451tg(327°) = -0.64941tg(328°) = -0.62487tg(329°) = -0.60086tg(330°) = -0.57735tg(331°) = -0.55431tg(332°) = -0.53171tg(333°) = -0.50953tg(334°) = -0.48773tg(335°) = -0.46631tg(336°) = -0.44523tg(337°) = -0.42447tg(338°) = -0.40403tg(339°) = -0.38386tg(340°) = -0.36397tg(341°) = -0.34433tg(342°) = -0.32492tg(343°) = -0.30573tg(344°) = -0.28675tg(345°) = -0.26795tg(346°) = -0.24933tg(347°) = -0.23087tg(348°) = -0.21256tg(349°) = -0.19438tg(350°) = -0.17633tg(351°) = -0.15838tg(352°) = -0.14054tg(353°) = -0.12278tg(354°) = -0.1051tg(355°) = -0.08749tg(356°) = -0.06993tg(357°) = -0.05241tg(358°) = -0.03492tg(359°) = -0.01746tg(360°) = 0

Котангенс угла

Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:

Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:

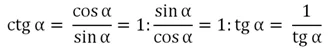
Почти во всех задачах с помощью формулы

можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.

Значения этой ф-ции рассчитываются так:

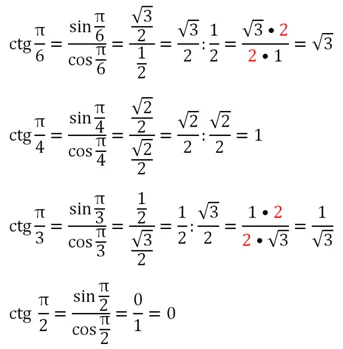
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.

График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:

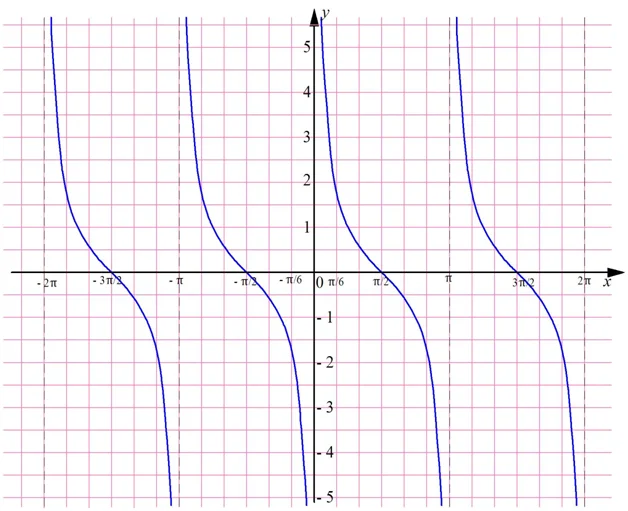
Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.

Для сравнения покажем на одной плоскости графики тангенса и котангенса:

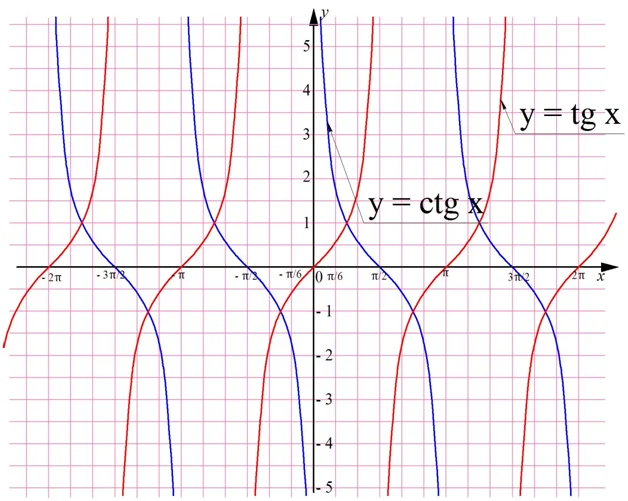
Котангенс, как и тангенс – нечетная ф-ция, то есть

ctg (– x) = – ctgx

Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.

Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.