Тангенс угла
В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 90. Угол в котором меньше 90 градусов — называется острым. Угол в котором больше 90 градусов — называется тупым. В развернутом угле 180 градусов.
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла — называется катетом.

Синус и косинус находятся с помощью катета и гипотенузы, а именно:
sinA = a/ccosA = b/c
Формула тангенса
tg A = a/b
другими словами определение тангенса — это деление противоположного катета на прилежащийСуществует ещё одна равносильная формула тангенса
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Обозначения для основных углов:тангенс 30 — 0,577тангенс 45 — 1,000тангенс 60 — 1,732
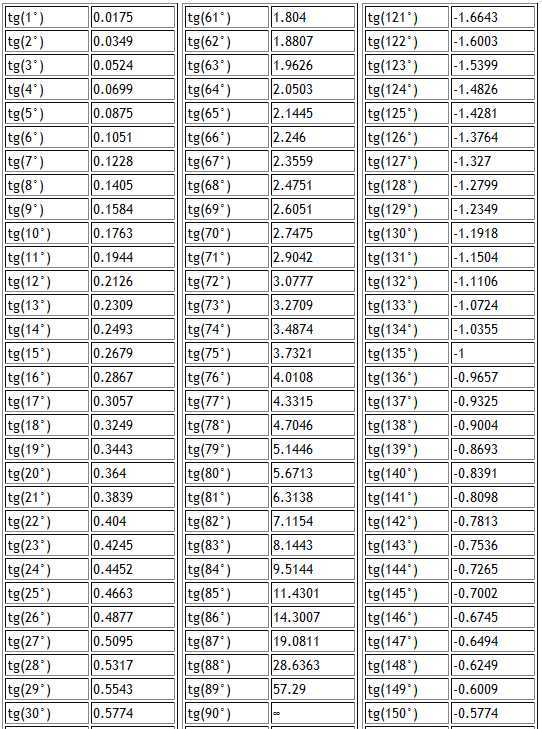
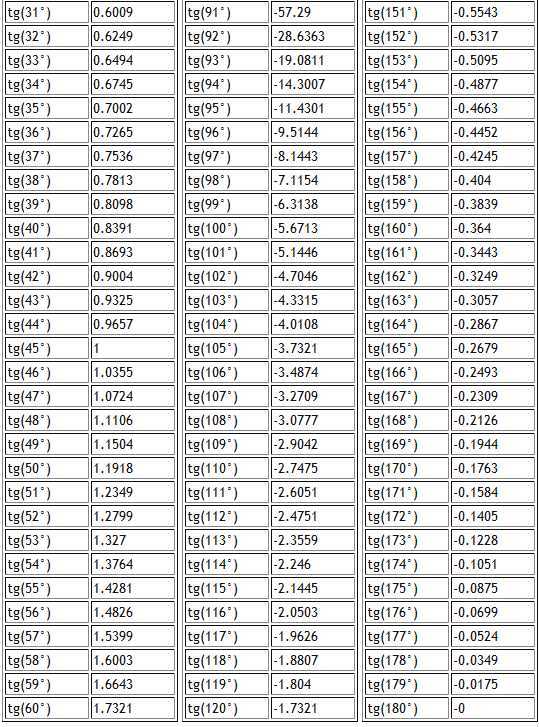
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.
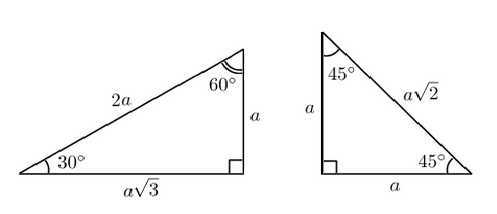
В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.Во втором случае гипотенуза превышает катет в ?2 раз.
отправить донат
Определение и свойства тангенса
Тангенс — это одна из тригонометрических функций, которая определяется отношением противолежащего катета к прилежащему катету в прямоугольном треугольнике.
Тангенс угла равен отношению синуса угла к косинусу угла. Таким образом, для определения тангенса угла необходимо знать значения синуса и косинуса этого угла.
Тангенс 30 градусов можно выразить через значения синуса и косинуса этого угла. Синус 30 градусов равен 0.5, а косинус 30 градусов равен √3/2. Подставляя эти значения в формулу, получим:
тангенс 30 градусов = синус 30 градусов / косинус 30 градусов = 0.5 / (√3/2) = 0.5 * 2 / √3 = 1 / √3.
Таким образом, тангенс 30 градусов равен 1 / √3, что можно упростить до √3 / 3.
Свойства тангенса:
- Значение тангенса угла лежит в интервале от минус бесконечности до плюс бесконечности.
- Тангенс прямого угла равен бесконечности.
- Тангенс угла больше 0, если угол находится в первой или третьей четвертях, и меньше 0, если угол находится во второй или четвертой четвертях.
- Тангенс периодическая функция с периодом π.
Таким образом, зная определение и свойства тангенса, можно вычислять его значения и применять в решении различных задач из геометрии и физики.
Определение тангенса
Тангенс 30 градусов — это отношение противоположной стороны треугольника к его прилежащей стороне, когда угол между ними составляет 30 градусов.
Для нахождения значения тангенса 30 градусов можно воспользоваться тригонометрическим кругом или таблицей значений тригонометрических функций.
Чему равен тангенс 30 градусов? Зная, что тангенс выражается формулой tg(α) = sin(α) / cos(α), мы можем посчитать значение тангенса 30 градусов. Так как sin(30) = 1/2 и cos(30) = √3/2, подставляя значения в формулу, получаем: tg(30) = (1/2) / (√3/2) = 1/√3 = √3/3.
Свойства тангенса
Тангенс — это основная тригонометрическая функция, которая определяется как отношение противоположной стороны к прилежащей стороне прямоугольного треугольника. Одним из свойств тангенса является его периодичность: значение тангенса повторяется с периодом в 180° или π радиан.
Когда мы говорим о значении тангенса, часто имеют в виду значения для углов, равных 0°, 30°, 45°, 60° и 90°. Тангенс 30 градусов — это отношение противоположной стороны к прилежащей стороне в прямоугольном треугольнике, у которого один из углов равен 30°.
Чему равен тангенс 30 градусов? Для угла 30° тангенс равен √3 / 3 или примерно 0,5774. Это означает, что противоположная сторона в прямоугольном треугольнике длиной 1 единица будет составлять около 0,5774 единиц от прилежащей стороны.
Значения тангенса можно также представить в виде таблицы:
| Угол (°) | Тангенс |
|---|---|
| 0° | |
| 30° | √3 / 3 |
| 45° | 1 |
| 60° | √3 |
| 90° | ∞ |
Таким образом, тангенс 30 градусов равен примерно 0,5774 и является часто используемым значением в различных вычислениях и применениях, связанных с геометрией и физикой.
Таблица тангенсов
| х (°)» порядок данных=»x (°)«стиль = «минимальная ширина: 34,7656%»; ширина:34,7656%;»>x (°) | х (строка)» порядок данных=»x (рад)«стиль = «минимальная ширина: 33,5938%; ширина:33,5938%;»>x (строка) | х»заказ данных=»tg x«стиль = «минимальная ширина: 31,6406%»; ширина:31,6406%;»>тг х |
| -90° | -π/2 | -∞ |
| -71,565° | -1,2490 | -3 |
| -63,435° | -1,1071 | -2 |
| -60° | -π/3 | 3″ порядок данных=»-√3″>-√3 |
| -45° | -π/4 | -1 |
| -30° | -π/6 | 3″ порядок данных=»-1/√3″>-1/√3 |
| -26,565° | -0,4636 | -0,5 |
| 0° | ||
| 26,565° | 0,4636 | 0,5 |
| 30° | π/6 | 3″ порядок данных=»1/√3″>1/√3 |
| 45° | π/4 | 1 |
| 60° | π/3 | 3″заказ данных=»√3″>√3 |
| 63,435° | 1.1071 | 2 |
| 71,565° | 1.2490 | 3 |
| 90° | π/2 | ∞ |
презентация потеме Функция тангенса, ее график и свойства. презентация к уроку по алгебре (10 класс) по теме
Слайд 1
Функция у = tg х и построение ее графика. .
Слайд 3
Определяем цели учебной деятельности 1.Выделите слова и словосочетания, встречаемые впервые. 2.Определите, знаете ли Вы точное значение этих слов, а также тех слов и словосочетаний, которые уже встречались Вам, но точные их значения и определения остаются Вам пока неизвестными.
Слайд 4
Определяем цели учебной деятельности 3 . Какие новые определения и значения каких понятий необходимо будет усвоить в рамках изучения данной темы? 4. Какие умения нужно будет выработать? 5. Какие правила, алгоритмы, способы действий Вам неизвестны , и для решения каких задач они Вам будут нужны?
- Слайд 5
- Тангенс.
- Слайд 6
Предполагаемые цели учебной деятельности учеников 1. Определение функции тангенса, свойств этой функции 2.Построение графика функции тангенс по таблице значений и тем свойствам, которые известны для тангенса (алгоритм построения). Узнать, н а какой линии находятся тангенсы углов.
Слайд 7
Находим ответы на вопросы в учебнике. Стр.17 -стр.18: определение , л иния тангенсов углов, о бласть определения, о бласть значений, с войства тангенса, известные вам на сегодняшний день.
- Слайд 8
- Рисунок 10 из учебника
- Слайд 9
Функция у = tg х. Определение. Числовая функция, заданная формулой у = tg х , называется функцией тангенса. Тангенс угла – отношение ординаты точки на единичной окружности, соответствующей данному углу, к абсциссе этой точки. А где находятся тангенсы углов?
- Слайд 10
- Тригонометрический круг
- Слайд 11
- диктант a = 185 градусов a = – 185 градусов a = 102 a = – 102 a = 250 a = – 250 a = 375 a = 145 a = – 145 a = 225 a = – 315 a = 210 a = 590 a = – 15 1Углом какой четверти является угол a , если:
- Слайд 12
диктант 2. Вычислите : 1 вариант. cos 180 + 5sin 90 sin 180 – 3 cos 0 5ctg 90 – 7tg 180 sin 60 + cos 30 2 вариант. cos 0 + 3sin 90 sin 270 – 2cos 180 6tg 180 + 2ctg 90 1 + ctg 270 – 5 tg 360
Слайд 13
Нормы оценок 1.Все задания верны – оценка «5» 2. 1-2 ошибки – оценка «4» 3. 3- 5 ошибок – оценка «3» 4. более 5 ошибок – беру дополнительное домашнее задание. Успехов в учебе!
Слайд 14
Ответы к диктанту. 1вариант. 1. III,II,II,III,III,II,I. 2. 4,-3,0. 2 вариант. 1.II,III,III,I,III,III,IV. 2. 0,2,4. Задание . Заполнить в тетради таблицу значений для построения графика у = tg х. Работа в парах.
Слайд 15
Построение графика. Составляем план построения графика, пользуясь учебником.
Слайд 16
План построения графика. 1 . Правильно выбери единичный отрезок. 2. Н айди область определения. 3 Проведи прямые у = π/ 2 + π n , где n принадлежит целым числам. 4. Построй график. Работаем в парах.
- Слайд 17
- Линия тангенса
- Слайд 18
- График функции в 1 четверти у = tg x x y 0 1
- Слайд 19
- у = tg x х у y = tg x
- Слайд 20
Выполнение заданий. №37(В),33(г). Устно составить план выполнения задания, обговорить в парах. Рефлексия. Ответьте на вопросы: Какие новые знания вы приобрели на этом уроке? Какие новые умения? Все ли цели урока были достигнуты? .
Слайд 21
Домашняя работа. 1. Построить по аналогичному график функции котангенс. 2.Уметь доказывать по рис 10 из учебника, что касательная к числовой окр ., проведенная в точке (1,0), является линией тангенсов.
36( а,б,в ),38(а), 39( а,в,г ) Творческое задание. По рис.11учебника, доказать, что касательная прямая, проведенная в точке (0,1) к числовой окружности, является линией котангесов . Спасибо за урок.
Слайд 22
Спасибо за урок.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Определение значения тангенса угла 30…360 градусов
\
\
\
\
Угловые значения tan 90°, 270° — не имеет значения и не определяются, согласно основным законам геометрии и математики.
Таблица 1. Определение угловых значений тангенса.
| α | 0° | 30° | 45° | 60° | 90° | 120° |
| tanα | \ | 1 | \ | не определяется | \ | |
| радиан | \ | \ | \ | \ | \ |
Продолжение таблицы 1.
| α | 135° | 150° | 180° | 210° | 225° | 240° |
| tanα | -1 | \ | \ | 1 | \ | |
| радиан | \ | \ | π | \ | \ | \ |
Продолжение таблицы 1.
| α | 270° | 300° | 315° | 330° | 360° |
| tanα | — | \ | -1 | \ | |
| радиан | \ | \ | \ | \ | 2π |
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для лучшего восприятия.
Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу 2.
Таблица 2. Нестандартные углы функции тангенс.
| угол | π/12=15 | π/10=18 | π/8=22,5 | π/5=36 | 3π/10=54 | 3π/8=67,5 | 2π/5=72 |
| tan | \ | \ | \ | \ | \ | \ | \ |
Свойства тангенса
Ниже в табличной форме представлены основные свойства касательной с формулами.
| Свойство | Формула |
| Симметрия | tg (-α) = -tg α»порядок данных=»tg (-α) = -tg α»>tg (-α) = -tgα |
| Симметрия | tg (90°- α) = ctg α»data-order=»tg (90°- α) = ctg α»>tg (90°- α) = ctg α |
| Тригонометрические тождества | загар α = грех α / потому что α» data-order=»tg α = sin α / cos α»>tg α = sin α / cos α |
| tg α = 1 / ctg α «данные-порядок=»tg α = 1 / ctg α»>tg α = 1 / ctg α | |
| Тангенс двойного угла | tg 2α = 2 tg α / (1 — tg2 α)» data-order=»tg 2α = 2 tg α / (1 — tg2 α)»>tg2α = 2tgα / (1 — tg2α) |
| Тангенс суммы углов | tg (α+β) = (tg α + tg β) / (1 — tg α tg β)» data-order=»tg (α+β) = (tg α + tg β) / (1 — tg α tg β)»>tg (α+β) = (tg α + tg β) / (1 — tg α tg β) |
| Тангенс разности углов | tg (α-β) = (tg α — tg β) / (1 + tg α tg β)» data-order=»tg (α-β) = (tg α — tg β) / (1 + tg α tg β)»>tg (α-β) = (tg α — tg β) / (1 + tg α tg β) |
| Сумма тангенсов | tg α + tg β = sin (α + β) / cos α cos β» data-order=»tg α + tg β = sin (α + β) / cos α cos β»>tg α + tg β = sin (α + β) / cos α cos β |
| Тангенс разница | tg α — tg β = sin (α — β) / cos α cos β» data-order=»tg α — tg β = sin (α — β) / cos α cos β»>tg α — tg β = sin (α — β) / cos α cos β |
| Произведение касательных | tg α tg β = (tg α + tg β) / (ctg α + ctg β)» data-order=»tg α tg β = (tg α + tg β) / (ctg α + ctg β)»>tg α tg β = (tg α + tg β) / (ctg α + ctg β) |
| Произведение тангенса и котангенса | tg α ctg β = (tg α + ctg β) / (ctg α + tg β)» data-order=»tg α ctg β = (tg α + ctg β) / (ctg α + tg β)»>tg α ctg β = (tg α + ctg β) / (ctg α + tg β) |
| Касательная производная | tg’ x = 1 / cos2 (x)» порядок данных=»tg’ x = 1 / cos2 (x)»>tg’ х = 1 / cos2 (х) |
| Касательный интеграл | ∫ тангенс x dx = -ln |cos x| +C»заказ данных=»∫ tg x dx = -ln |cos x| + C»>∫ тангенс х dx = -ln | cos х | + C |
| Формула Эйлера | tg x = (eix — e-ix) / i(eix + e-ix)» data-order=»tg x = (eix — e-ix) / i(eix + e-ix)»>tg x = (eix — e-ix) / i(eix + e-ix) |
Что такое тангенс
Тангенсом какого-либо острого угла \(\alpha (tg \alpha)\) называют величину, выражающую отношение противоположного катета (а) к прилегающему катету (b) в треугольнике с углом 90°, то есть: \(tg \alpha = \frac{a}{b}\)
Понятие тангенса угла можно проиллюстрировать таким образом:
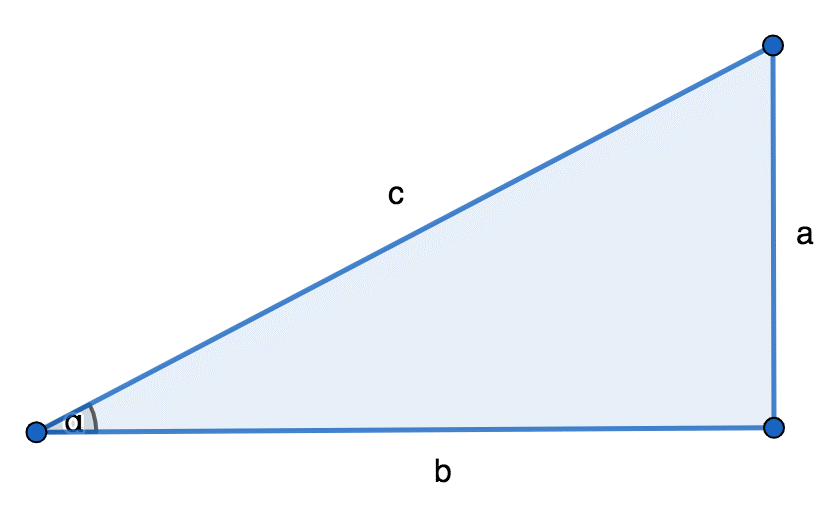
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Пример 1
Рассмотрим наглядный пример. Предположим, что катеты в треугольнике из определения тангенса имеют следующие значения: a = 3 b = 4 В таком случае справедливо записать выражение для расчета тангенса угла: \(tg \alpha = \frac{a}{b} = \frac{3}{4} = 0,75\)
Тангенс — это отношение…
Итак, есть два определения:
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Это определение удобно использовать при изучении геометрических фигур. Он позволяет кроме вычисления гипотенузы находить углы или катеты. Выбирая на произвольных фигурах прямоугольные треугольники, упрощается задача изучения свойств изучаемых объектов.
- Тангенс — это отношение синуса к косинусу.
Благодаря такому определению многие тригонометрические формулы приобретают более практичный вид, становятся легче для восприятия.
Утвержденные обозначения:
Вместо «тангенс угла альфа» пишут: tgα. На калькуляторах, в различных программах для ЭВМ и ПК закрепилось другое обозначение: tan (α).
Таблица тангенсов от 0° до 180°
|
|
|
|
|
График функции y=tg x
Как построить график функции y=tg x? Для начала рассмотрим график тангенса на интервале (-π/2;π/2).
Число π округлим до целого:
Единичный отрезок берём длиной в 2 клеточки тетради. В этом случае числу π соответствует отрезок длиной в 6 клеточек, числу π/2 — 3 клеточки, π/6 — 1 клеточка, π/4 — 1,5 клеточки, π/3 — 2 клеточки.
- В область определения функции y=tg x не входят числа
- Прямые
для графика тангенса являются вертикальными асимптотами, то есть график к ним стремиться, но никогда не достигнет. Асимптоты принято изображать пунктирными линиями.
- Составим таблицу значений тангенса на промежутке [0;π/2):
- На координатной плоскости отмечаем полученные точки и асимптоты.
- Так как y=tg x — нечётная функция, её график симметричен относительно начала координат:
Поскольку функция tg x — периодическая с периодом T=π, график тангенса, взятый на интервале (-π/2;π/2), повторяется влево и вправо, на плюс и на минус бесконечность:
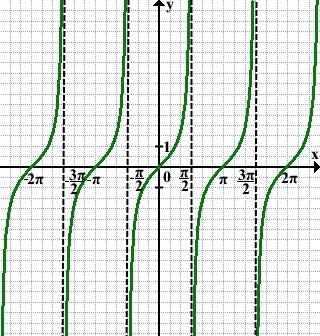
График функции y=tg x
Графики функций, в том числе, тригонометрических, в алгебре могут быть использованы при решении уравнений, неравенств, при решении других заданий.
Стандартные углы
Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
- Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
\
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:
\
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
\
И с углом 30°:
\
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:
\
Итак, мы знаем синус
Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$
Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
И наоборот:
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.





























