Примеры задач на дробные выражения для 6 класса
Пример 5
79 чисел в сумме дают 42. Найдите это число.
Решение.
Пусть неизвестное число равно х. Тогда 79 х равно 42:
79х=42.
Задача сводилась к решению уравнения. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Мы получаем:
79x=42 x=42:79 Чтобы разделить натуральное число на обыкновенную дробь, мы представляем натуральное число в виде дроби со знаменателем 1 и умножаем ее на дробь, которая будет обратной дроби 79 x=421 *97 Мы умножая числитель на числитель, знаменатель на знаменатель: x=42*91*7 Сокращаем дробь: ищем общий делитель числителя и знаменателя. Числитель и знаменатель делятся на 7 42 делится на 7 и 7 делится на 7 x=6*91*1 x=541 x=54.
Ответ: 54.
Пример 6
Используйте материалы урока для самостоятельного решения задачи.
63% от числа равно 126. Найдите это число.
Решение.
Переводим 63% в десятичную дробь. Получаем 0,63.
63%:100%=0,63.
Тогда 0,63 от искомого числа равно 126. Обозначим искомое число через x.
Получаем уравнение:
0,63х=126.
Решаем уравнение.
0,63x=126 x=126:0,63 Чтобы разделить число на десятичную дробь, мы избавляемся от запятой в делителе. Для этого умножаем каждую составляющую выражения на сто. Получаем: x=12600:63 И считаем: x=200.
Ответ: искомое число 200.
Задача 3
Иван прошел 250 метров, что составляет 47 метров местной экологической тропы. Какова длина экологической тропы?
Решение.
Пусть длина всей экологической тропы х метров. Затем мы получаем уравнение для нахождения всего пути:
47х=250.
Чтобы найти неизвестный множитель x, мы делим произведение на известный множитель.
x=250:47 Представим натуральное число в виде дроби 2501 x=2501:47 Чтобы разделить две дроби друг на друга, переписываем первую дробь, меняем знак деления на знак ; ; (найти обратную дробь) x=2501*74 Умножаем числитель на числитель, знаменатель на знаменатель x=250*71*4 Сокращаем дробь: делим числитель и знаменатель на одно и то же число. 250 и 4 делятся на 2 x=125*71*2 x=8752 Разделите числитель на знаменатель. Получаем десятичную дробь: x=437,5.
Ответ: длина экологической тропы 437,5 метра.
Задача 4
Ирина выполнила 25% заданий, это 4 примера. Сколько примеров нужно решить Ирине.
Решение.
Пусть общее количество примеров равно х. Тогда 25% от х равно 4.
Составим уравнение: 25%x=4.
Чтобы решить уравнение, нужно найти неизвестный множитель x: разделить произведение на известный множитель.
Преобразование процентов в дроби: 25%:100%=0,25.
Получаем уравнение: 0,25x=4.
0,25x=4 x=4:0,25 Чтобы разделить натуральное число на десятичную дробь, умножьте каждую часть на сто: x=4*100:0,25*100 x=400:25 x=16.
Получается, что Ирине было предложено решить 16 примеров, из которых она уже решила 4. Значит, ей предстоит решить:
16-4=12 примеров
Ответ: Ирине нужно решить 12 задач.
Нахождение дроби от числа на примере
Задача: В классе 30 учеников. 1/3 часть всех учеников составляю девочки. Вычислите чему равно количество девочек в классе.
В данной задаче целой величиной является количество учеников в классе — 30, а дробью, то есть частью — 1/3. Для того, чтобы вычислить количество девочек в классе мы должны дробь 1/3 умножить на общую величину — 30.
30 * 1/3 = 30/1 * 1/3 = 30 * 1 / 1 * 3 = 30 / 3 = 10 учеников.
Для того, чтобы умножить целое число на дробь нужно:
- представить целое число в виде обыкновенной дроби (30 = 30/1).
- числитель первой дроби умножить на числитель второй дроби.
- знаменатель первой дроби умножить на знаменатель второй дроби.
- первое произведение записать в числителе новой дроби, а второе в знаменателе.
Вычисление дроби от числа
До сих пор мы с вами находили доли (дроби) от одного. Но как быть, если нам нужно найти часть не от $1$, а от какого-то другого числа?
Например, мы знаем, что в минуте $60$ секунд. Сколько будет секунд в $\frac{1}{3}$ минуты?
Показать ответ
Скрыть
Найдем треть от $60$:$\newline$ $60:3=20$ секунд.
{"questions":[{"content":"В двух клетках сидят $2$ белых и $3$ черных кролика. Между кроликами нужно поровну разделить $10$ морковок.`image-1`Сколько морковок необходимо положить к черным кроликам?`choice-14`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/08/kroliki.svg"},"choice-14":{"type":"choice","options":,"explanations":,"answer":}},"step":1,"hints":}]}
Операции над дробями
С дробями можно совершать различные арифметические операции.
Сложение
Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.
Далее — выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.
В конце, если возможно, сократить полученную дробь.
Например:
Вычитание
Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.
Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.
Например:
Умножение
Для этого умножаются числители и записывается результат, как числитель дроби.
Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.
Например:
Деление
Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.
Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.
Например:
Сокращение
Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.
В итоге получается равную дробь, имеющая меньший знаменатель и числитель.
Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.
Значительно упростит сокращение раскладывание знаменателя и числителя на множители.
Например:
Вопросы и ответы
А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них
Какие дроби называются простыми?
Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.
Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название — десятичные.
Правильные дроби те, у которых модуль знаменателя больше модуля числителя.
Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.
Нельзя делить на 0.
Если делить на 1 — будет такое же число.
Если делить 0 на любое число, получится 0.
Когда она больше 0.
Когда перед положительной дробью ставится знак «–».
Что такое степени с дробями?
Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.
При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.
Как пользоваться калькулятором дробей?
Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.
Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор логарифмов. Вычислите онлайн натуральные, десятичные логарифмы (или с другим основанием) с решением.
- Возведение дроби в степень. Возведите онлайн любую дробь (десятичную и обыкноенную) в любую степень.
- Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
- Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
- Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
- Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
- На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
- На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.
Нахождение числа по его дроби
Замечание 1
Чтобы найти число по данному значению его дроби нужно это значение разделить на дробь.
Пример 1
Антон за неделю учебы заработал три четверти отличных отметок. Сколько всего отметок получил Антон, если отличных отметок было 6.
Решение.
По условию задачи $6$ отметок – это $\frac{3}{4}$.
Найдем количество всех отметок:
$6\div \frac{3}{4}=6 \cdot \frac{4}{3}=\frac{6 \cdot 4}{3}=\frac{2 \cdot 3 \cdot 4}{3}=2 \cdot 4=8$.
Ответ: всего $8$ отметок.
Пример 2
Выкосили $\frac{4}{9}$ пшеницы на поле. Найти площадь поля, если было скошено $36$ га.
Решение.
По условию задачи $36$ га – это $\frac{4}{9}$.
Найдем площадь всего поля:
$36\div \frac{4}{9}=36 \cdot \frac{9}{4}=\frac{36 \cdot 9}{4}=\frac{4 \cdot 9 \cdot 9}{4}=81$.
Ответ: площадь всего поля $81$ га.
Пример 3
За один день автобус проехал $\frac{2}{3}$ маршрута. Найти продолжительность намеченного маршрута, если за день автобус проехал $350$ км?
Решение.
По условию задачи $350$ км – это $\frac{2}{3}$.
Найдем продолжительность всего маршрута автобуса:
$350\div \frac{2}{3}=350 \cdot \frac{3}{2}=\frac{350 \cdot 3}{2}=175 \cdot 3=525$.
Ответ: продолжительность намеченного маршрута $525$ км.
Пример 4
Рабочий поднял производительность своего труда на $%\ $и сделал за такой же срок на $24$ детали больше, чем было запланировано. Найти количество деталей, запланированных для выполнения рабочим.
Решение.
По условию задачи $24$ детали = $8\%$, а $8\% = 0,08$.
Найдем количество деталей, запланированных для выполнения рабочим:
$24\div 0,08=24\div \frac{8}{100}=24 \cdot \frac{100}{8}=\frac{24 \cdot 100}{8}=\frac{3 \cdot 8\ cdot 100}{8}=300$.
Ответ: запланировано $300$ деталей для выполнения рабочим.
Пример 5
В цехе отремонтировали $9$ станков, что составляет $18\%$ всех станков цеха. Сколько станков находится в цехе?
Решение.
По условию задачи $9$ станков = $18\%$, а $18\% = 0,18.$
Найдем количество станков в цехе:
$9\div 0,18=9\div \frac{18}{100}=9 \cdot \frac{100}{18}=\frac{9 \cdot 100}{18}=\frac{9 \cdot 100}{2 \cdot 9}=\frac{100}{2}=50$.
Ответ: в цехе $50$ станков.
Еще одна формула сложных процентов.
Если процентная ставка дана не в годовом исчислении, а непосредственно для периода начисления, то формула сложных процентов выглядит так.
S = K * ( 1 + P/100 ) N
Где: S — сумма депозита с процентами, К — сумма депозита (капитал), P — процентная ставка, N — число периодов начисления процентов.
Пример. Принят депозит в сумме 100 тыс. рублей сроком на 3 месяца с ежемесячным начислением процентов по ставке 1.5 процента в месяц.
S = 100000 * (1 + 1.5/100) 3 = 104 567.84 Sp = 100000 * ((1 + 1.5/100) 3 — 1) = 4 567.84
Избавьтесь от утомительных расчетов с помощью этих Excel-таблиц >>>
- Платежный календарь
- Расчет себестоимости
- Расчет инвестиционных проектов
- Финансовый анализ
- Точка безубыточности. Рентабельность продаж Подробнее…
Платежный календарь. График и прогноз платежей и поступлений
- Платежные Календари на месяц, 3 месяца и год
- Деб.и Кред. задолженность
- Отсрочка, просроченные, с наступающим сроком
- Контроль оплаты
- Расчет ожидаемого остатка
- Кассовый разрыв Подробнее…
Расчет себестоимости и рентабельности продукции (услуг)
- Себестоимость
- Рентабельность
- Маржинальный анализ
- Точка безубыточности
- Расходы в 10 валютах Подробнее…
Расчет инвестиционных проектов
- Дисконтир. потоки
- WACC, NPV, IRR, ROI, PI
- Срок окупаемости
- Устойчивость проекта
- Расчет и Сравнение семи проектов Подробнее…
Финансовый анализ МСФО
- Вертикальный и горизонтальный Анализ баланса и P&L
- 36 коэффициентов
- Динамика за 5 периодов
- Риск банкротства
- ДДС прямым и косвенным методом
- Отчет об источниках и использовании денежных средств Подробнее…
Финансовый анализ РСБУ (Россия)
- Вертикальный и горизонтальный Анализ баланса и ОПУ
- 70 коэффициентов
- Динамика за 8 периодов
- Риск банкротства Подробнее…
Точка безубыточности. Рентабельность продаж
- Расчет доходности при большом ассортименте
- Прибыль
- Наценка
- Минимальная наценка
- Маржинальный анализ
- Точка безубыточности Подробнее…
Оценка стоимости бизнеса
- Все три основных подхода
- Доходный
- Рыночный (сравнительный)
- Затратный (имущественный) Подробнее…
https://youtube.com/watch?v=51iZYRQeASo%26pp%3DygVL0JrQsNC6INC-0L_RgNC10LTQtdC70LjRgtGMINC00L7Qu9GOINC-0YIg0YfQuNGB0LvQsCDQsiDQstC40LTQtSDQtNGA0L7QsdC4
Нахождение дроби от числа
Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, от пиццы это половина пиццы:
Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет от десяти сантиметров:
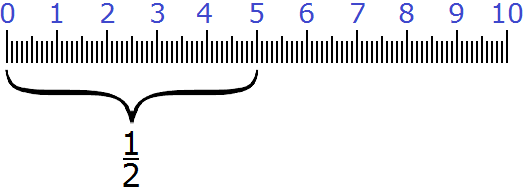
Как вы уже догадались от десяти сантиметров составляют пять сантиметров. Ведь это простейшая дробь, которая означает половину от чего-то. У нас было десять сантиметров. Мы разделили эти десять сантиметров пополам и получили пять сантиметров.
Попробуем узнать, сколько составляет от одного часа. Вспоминаем, что час это 60 минут. Нам нужно найти (половину) от 60 минут. Нетрудно догадаться, что половина от 60 минут это 30 минут. Значит от одного часа составляет 30 минут или полчаса.
Попробуем найти от одного центнера. Центнер это 100 кг. Требуется найти (половину) от 100 кг. Нетрудно догадаться, что половина от 100 кг это 50 кг. Значит от одного центнера составляют 50 кг.
Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём от числа 12 .
Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит числа 12 составляет число 6.
Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:

Пусть требуется найти от этих десяти сантиметров. Читаем первую часть правила:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби
Итак, делим десять сантиметров на знаменатель дроби . Знаменатель этой дроби равен числу 2. Поэтому делим десять сантиметров на 2
Читаем вторую часть правила:
и полученный результат умножить на числитель дроби
Итак, умножаем пять сантиметров на числитель дроби . Числитель дроби в данном случае единица. Поэтому умножаем пять сантиметров на единицу:
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют пять сантиметров:
Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.
В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби , мы тем самым указали, что берем одну часть из двух.
Пример 2. Найти
Применим правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Сначала делим 10 сантиметров на знаменатель дроби
Получили два сантиметра. Этот результат нужно умножить на числитель дроби
Мы нашли
Весь процесс решения можно увидеть на следующем рисунке:
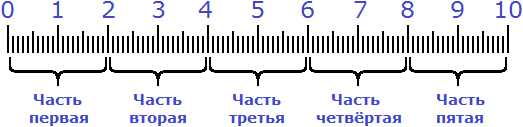
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:
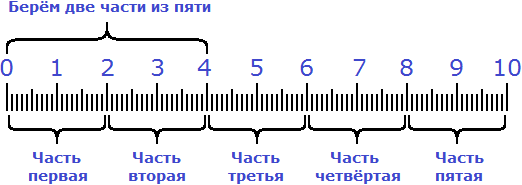
Пример 3. Найти
Чтобы найти
Итак, сначала делим число 56 на знаменатель дроби
Теперь умножаем полученное результат на числитель дроби
Получили ответ 21. Значит
Пример 4. Найти от одного часа.
Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.
Сначала разделим 60 минут на знаменатель дроби
60 мин : 4 = 15 мин
Теперь умножим полученные 15 минут на числитель дроби
15 мин × 2 = 30 мин
Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.
Пример 5. Найти
Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби
100 см : 5 = 20 см
Теперь умножим полученные 20 см на числитель дроби
20 см × 4 = 80 см
Получили ответ 80 см. Значит
Соглашение об определении долей
Выкуп доли В отделении материнского капитала распределение. процентнДля детей и супруга. Для расчета суммы будущих долей должны быть рассчитаны заранее или в течение 6 месяцев после приобретения жилья. Для получения дополнительной информации см. статью «Распределение доли Дополнительную информацию см. в статье «Пособие на ребенка при оформлении пособия по беременности и родам».
- В связи с частыми изменениями в законодательстве информация порой устаревает быстрее, чем мы успеваем ее обновлять на сайте.
- Все случаи очень индивидуальны и зависят от множества факторов. Базовая информация не гарантирует решение именно Ваших проблем.
Составление пропорции
Пропорция — определенное соотношение частей между собой.
С помощью метода пропорции можно рассчитать любые %. Выглядит это так:
Читается: a относится к b так, как с относится к d
Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение
Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
|
Ответ: купить спортивную футболку выгоднее на 194,6 рубля.
Есть случаи, при которых можно использовать простые дроби.
- 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
- 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
- 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
- 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
- 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
|
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Нахождение процента от числа
Особенно часто можно услышать об интересе в контексте финансовой отчетности: цены выросли на 15%, выручка упала на 5% и так далее.
Запись в виде 10% следует интерпретировать как 0,1
(mathbf{12%=0,12})
(mathbf{50%=0,5})
и так далее, то есть, чтобы получить десятичную дробь, равную числу в процентах, необходимо число процентов разделить на 100.
Поэтому, чтобы найти процент от числа, необходимо преобразовать проценты в десятичную дробь, а затем воспользоваться правилом нахождения дроби от числа: умножить число на дробь.
Например, вам нужно найти 5% от 200.
Первый шаг — преобразовать 5% в десятичную дробь:
(mathbf{5%=5div100=0,05})
Второй шаг – умножить найденную дробь на число:
(mathbf{0,05cdot200=10})
10 и составит 5% от 200.
Давайте рассмотрим еще несколько примеров.
Найдите 20% от 80:
(mathbf{20%=20div100=0,2})
(mathbf{0,2cdot80=16})
Также, если это кажется более удобным, можно преобразовать десятичную дробь в обычную и умножить на нее.
Найдите 50% от 234:
(mathbf{50%=50div100=0,5=frac{1}{2}})
(mathbf{234cdotfrac{1}{2}=frac{234}{2}=frac{117cdot2}{2}=117})
Как найти часть числа, выраженного дробью
- Как решить задачу с частями
- Как найти дробь
- Как разделить дробь на число
- Как выразить число
- Как извлечь корень из дроби
- Как находить долю от чего-то
- Как решать дроби по математике
- Как разделить дробь на целую: правило
- Как найти частное чисел
- Как найти целую часть
- Как посчитать дроби
- Как разбить число
- Как разделить в столбик
- Как умножить смешанные числа
- Как разделить дробь на целое число
- Как выразить в процентах дробь
- Как найти неправильную дробь
- Как делить обыкновенные дроби
- Как перевести дробь в число
- Как выделить неправильную дробь
- Как научиться решать дроби
- Как перевести дробь в обыкновенное число
- Как решать примеры с дробью
- Как перевести неправильную дробь
Нахождение числа по его дроби
Если известно сколько составляет часть от целого, то по известной части можно «восстановить» целое.
Для этого пользуемся правилом нахождения целого (числа) по его дроби (части).
Чтобы найти число по его части
, выраженной дробью, нужно данное число разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути. Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры выражены дробью 15/23 от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части, и 15 таких частей составляют 240 км (числитель дроби равен 15). Значит, можно найти, сколько составляет
Значит, чтобы найти весь путь (23 части, каждая из которых по 16 км) нужно:
Кратко запись решения такой задачи можно сделать следующим образом.
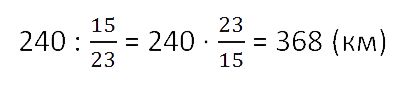
Ответ: поезд должен пройти 368 км.
Деление меньшего числа на большее
В жизни часто возникают ситуации, когда нужно разделить меньшее число на большее. Например, давайте представим ситуацию. Есть три друга:

И надо разделить два яблока поровну между ними. Как это сделать? Есть три друга, но только два яблока. Мы находимся в ситуации, когда требуется разделить меньшее число на большее (два яблока на три).
Для таких случаев предусмотрено следующее правило:
При делении меньшего числа на большее получается дробь, в числителе — делимое, а в знаменателе — делитель.
Применим это правило. В нем говорится, что при делении меньшего числа на большее получается дробь, в числителе стоит делимое, а в знаменателе делитель. Наша делимая — два яблока. Записываем цифру 2 в счетчик:
А наш делитель — это три друга (помните, что делитель показывает, на сколько частей нужно разделить делимое). Запишем тройку в знаменателе нашей дроби:
Смешно, но мусор
это ответ на нашу проблему. Каждый друг получит
яблоки. Почему так случилось?
Чтобы разделить два яблока на три, разрежьте ножом каждое яблоко на три части и разложите эти кусочки поровну между тремя друзьями:
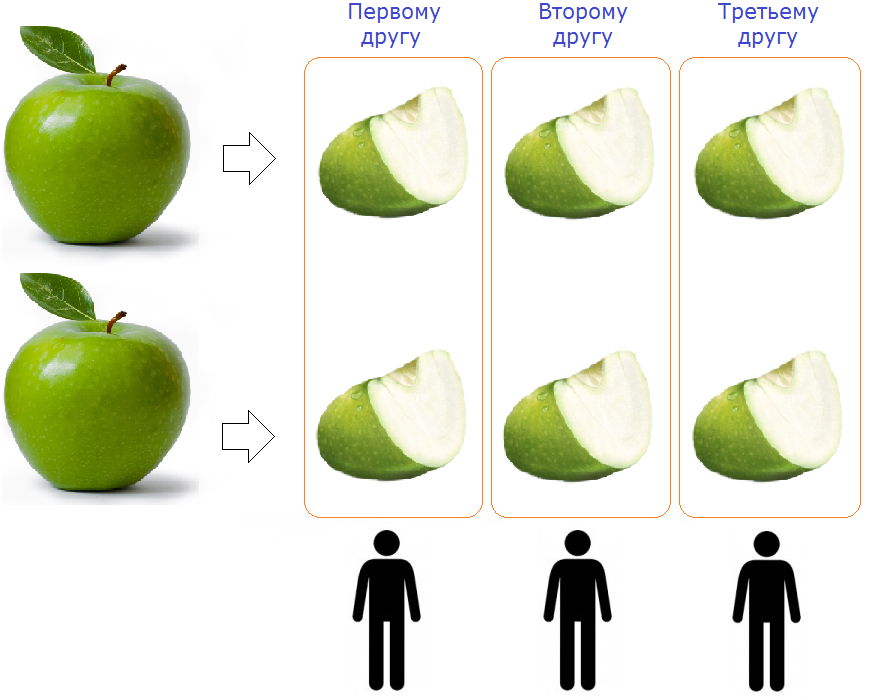
Как видно на картинке, каждое яблоко было разделено на три части и распределено поровну между тремя друзьями. Каждый друг получил
яблоки (две деревяшки).
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
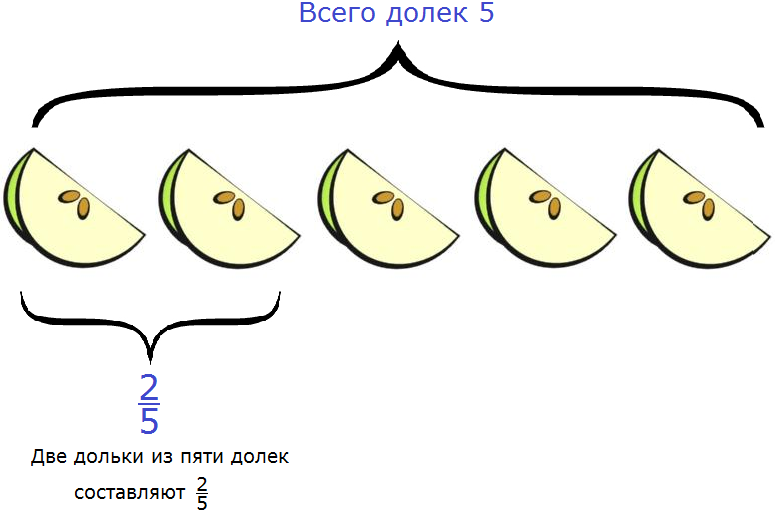
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь
Дробь
Также, эту дробь можно сократить на 2. После сокращения дроби
Дробь
Таким образом, число 2 составляет
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь
Получили аккуратную дробь
Число 5 составляет (одну третью) от числа 15.
Это можно даже проверить. Для этого нужно найти
Итак, найдём
Получили ответ 5. Значит задача была решена правильно.
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь
Получили ответ
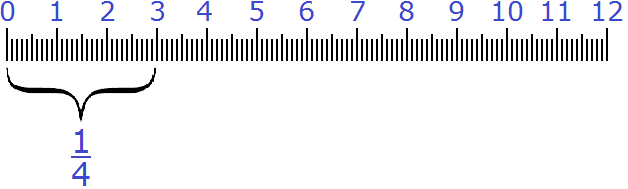
Проверим правильно ли мы решили эту задачу. Для этого найдём
Делим 12 на знаменатель дроби
Умножаем полученные 3 см на числитель дроби
Получили ответ 3 см. Значит задача была решена правильно.
Источник
Как найти дробь от числа
Рассмотрим правило, объясняющее, как найти дробь от числа, и его применение на примерах.
Чтобы найти дробь от числа
, нужно число умножить на эту дробь.
Найти дробь от числа:
Чтобы найти дробь от числа, надо число умножить на эту дробь. Умножаем их по правилу умножения числа на дробь: числитель умножаем на число, а знаменатель оставляем без изменения. Сокращаем 30 и 6 на 6. Таким образом,
Для нахождения дроби от числа число умножаем на дробь. 48 и 8 сокращаем на 8.
Чтобы найти четыре седьмых от 28, умножаем дробь на число. 28 и 7 сокращаем на 7 и перемножаем.
А как найти десятичную дробь от числа? Аналогично, умножив дробь на число. Например,
www.for6cl.uznateshe.ru
Как найти значение дроби (части) от целого
Теперь, когда мы понимаем, что дробь нам указывает на какую-то часть от целого, то есть 1/2 читается как одна вторая, а 23/56, — как двадцать три пятьдесят шестых, то нам хотелось бы манипулировать не просто понятиями как частями от целого, а именно их количественным значением. То есть скажем ваши родители, когда им говорят, что они получат премию в размере 2/3 от оклада всегда хотят знать, а сколько это в рублях, а именно не в частях.
Смотрите, опять к нашим яблокам. У нас есть корзинка с яблоками, и это условно целое, то есть корзинка это наша «полная часть». И нам скажем необходимо найти 2/5 от нее.

При этом мы знаем, что в корзине 20 яблок или это можно сказать как 5 частей по 4 яблока. Все это показано на рисунке. Однако нам надо найти лишь 2 части из 5, те которые подчеркнуты красной линией. Вы визуально можете уже посчитать, что это будет 8 яблок. Однако как же это можно было найти не столь наглядным образом, а именно исходя из расчетов? Легко!
Необходимо было наше целое, то есть 20 яблок, разделить на 5 частей, так как мы ищем значение именно из 5 частей и умножить на 2, так как именно две части нас интересуют.То есть 2/5 от 20 это 20/5*2=8 яблок.
Мне кажется все понятно. Теперь немного практики, в виде задачи, а потом перейдем к наглядным обучающим пособиям в виде онлайн — калькулятора для нахождения значения части в виде дроби от какого-то числа условно нашего целого.
Как найти дробь от числа

Одна из простой, но интересной темы – это как найти дробь от целого (от числа).
Как найти часть от целого? У нас есть какое-то значение и нам нужно найти долю или дробь от этого значения.
К примеру, пицца весит 540 г. Сколько весит кусок пиццы, если ее разделили на 6 одинаковых кусков?

Пиццу разрезали на 6 одинаковых кусков, значит, один кусок – это 1/6 от всей пиццы.
Начертим схему: чертим отрезок, разделим его на 6 равных частей. Удобнее начертить отрезок длиной 6 или 12 см (см. статью здесь).

Если пиццу разрезали, то и весь вес надо разделить: 540:6=90 (г)
Если нужно узнать вес двух кусков, т.е. 2/6

то эти 90 взять 2 раза: 90х2= 180 (г)
В итоге, 540 : 6 х 2, или, зная правила работы с дробями — 540 х 2/6.
Видим, что для того, чтобы найти 2/6 от целой пиццы нужно просто умножить общий вес на значение этой части — 2/6.
Как-то странно. Не правда ли? И, тем не менее: чтобы найти часть, мы умножаем, а не делим. Потому что если вспомнить, что дробь, вернее, горизонтальная черта дроби — это деление. Итак:

7/8 от 24 — 24:8х7=21
3/5 от 60 – 60:5х3=45
3/4 от 12 – 12:4х3=9
7/8 от 64 – 64:8х7=56
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 70
Источник
Задания для самостоятельного решения
Задание 1. Найдите от числа 30.
30 : 2 = 1515 × 1 = 15
Задание 2. Найдите от числа 30.
30 : 3 = 1010 × 2 = 20
Задание 3. Найдите от числа 30.
30 : 3 = 1010 × 3 = 30
Задание 4. Найдите от числа 48.
48 : 6 = 88 × 5 = 40
Задание 5. Найдите от числа 48.
48 : 8 = 66 × 5 = 30
Задание 6. Найдите от 120 см.
120 см : 3 = 40 см40 см × 2 = 80 см
Задание 7. Найдите от 150 см.
150 см : 3 = 50 см50 см × 2 = 100 см
Задание 8. Найдите целое число по дроби, если известно, что этого числа составляет число 16.
16 : 2 = 88 × 3 = 24
Задание 9. Найдите целое число по дроби, если известно, что этого числа составляет число 32.
32 : 1 = 3232 × 2 = 64
Задание 10. Найдите целое число по дроби, если известно, что этого числа составляет число 150.
150 : 5 = 3030 × 8 = 240
Задание 11. Найдите длину пути от дома до школы, если известно, что этого пути составляют 4 км.
4 км : 2 = 2 км2 км × 3 = 6 км
Задание 12. Найдите длину рулетки, если известно, что этой рулетки составляют 100 см.
100 см : 5 = 20 см20 см × 8 = 160 см
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Нахождение числа по его дроби
Если известно сколько составляет часть от целого, то по известной части можно «восстановить» целое.
Для этого пользуемся правилом нахождения целого (числа) по его дроби (части).
Чтобы найти число по его части
, выраженной дробью, нужно данное число разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути. Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры выражены дробью 15/23 от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части, и 15 таких частей составляют 240 км (числитель дроби равен 15). Значит, можно найти, сколько составляет
Значит, чтобы найти весь путь (23 части, каждая из которых по 16 км) нужно:
Кратко запись решения такой задачи можно сделать следующим образом.
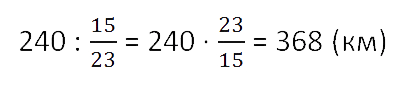
Ответ: поезд должен пройти 368 км.
Нахождение дроби от числа нахождение числа по известной величине его дроби
Существует ряд задач, в которых необходимо найти часть или дробь некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Задание.
Найти от 40.
Решение.
В рассматриваемом примере 40 — это заданное число, — дробь, задающая искомую часть. Тогда, согласно правилу, имеем:
Итак, получили, что от 40 равно 14 — искомая часть данного числа.
Ответ.
от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.
Задание.
В классе 12 мальчиков, что составляет части всех учеников класса. Сколько всего человек учится в классе?
Решение.
Искомое количество учеников
Ответ.
Всего в классе учится 15 человек.






























