Деление десятичных чисел

Что нужно сделать чтобы разделить десятичную дробь на 100

Чтобы разделить десятичную дробь на 100, нужно передвинуть запятую на две позиции влево. Например, если у нас есть число 347,3 и мы хотим разделить его на 100, то переносим запятую на две цифры влево и получаем 3,473. То есть результатом этого деления будет число 3,473. Точно так же можно разделить любую другую десятичную дробь на 100. Например, если у нас есть число 1078,42 и мы хотим разделить его на 100, то переносим запятую на две цифры влево и получаем 10,7842. Таким образом, результатом этого деления будет число 10,7842. В обоих случаях мы разделили исходные десятичные дроби на 100 путем перемещения запятой влево.

Деление меньшего числа на большее. Продвинутый уровень.

В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.

Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»

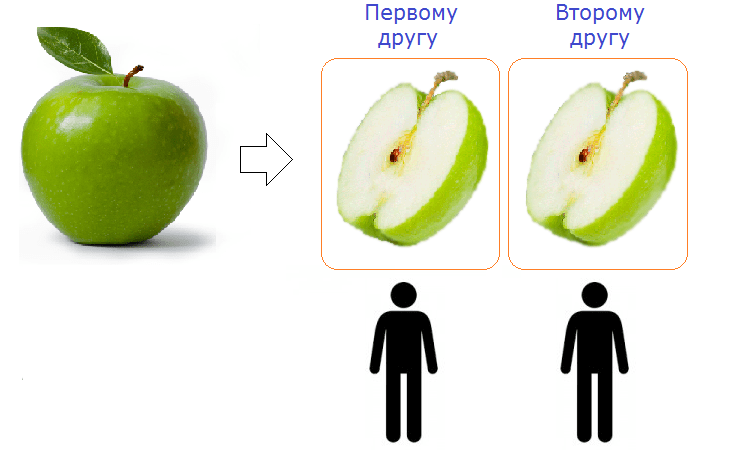
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.

Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.

При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.

Итак, разделим 1 на 2. Решим этот пример уголком:

Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице»

, то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:

Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:

Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:

Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:

Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10

Получили ответ 0,5. Значит дробь равна 0,5

Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко: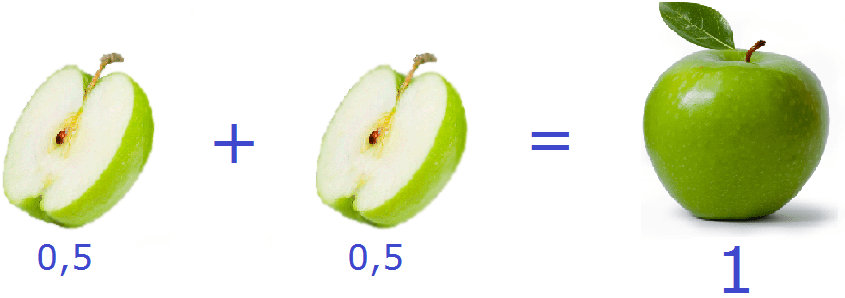

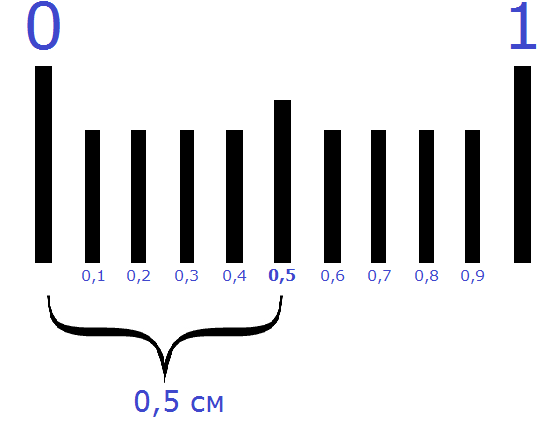
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см

Пример 2.
Найти значение выражения 4: 5

Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:

Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.

Завершаем пример, умножив 8 на 5, и получив 40:

Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8

Пример 3.
Найти значение выражения 5: 125

Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:

Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0

Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:

Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0

Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50

Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:

Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:

Завершаем пример, умножив 4 на 125, и получив 500

Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04

Как разделить обыкновенную дробь на обыкновенную дробь

Далее приводим новую дробь к несократимому виду, если это возможно. Для этого находим наименьшее общее кратное (НОК) знаменателей новой дроби и сокращаем числитель и знаменатель новой дроби на это НОК.

Например, разделим дробь 3/4 на дробь 2/3. Умножаем числитель первой дроби (3) на знаменатель второй (3), получаем 9. Умножаем знаменатель первой дроби (4) на числитель второй (2), получаем 8. Полученная дробь будет 9/8, которую можно сократить на наименьшее общее кратное знаменателей (8). Делаем сокращение и получаем несократимую дробь 9/8.

Таким образом, обыкновенную дробь можно разделить на другую обыкновенную дробь, выполнив указанные операции.

Общие принципы деления десятичных дробей

Конечные десятичные дроби и периодические десятичные дроби являются десятичной записью обыкновенных дробей. Следовательно, деление таких десятичных дробей по сути является делением соответствующих обыкновенных дробей. Таким образом, основной принцип деления конечных и бесконечных периодических дробей состоит в замене этих дробей обыкновенными дробями и последующем делении обыкновенных дробей.

Рассмотрим примеры деления десятичных дробей в этом свете.

Пример.

Выполните деление десятичной дроби 1,2 на десятичную дробь 0,48.

Решение.

Сначала осуществим , имеем 1,2=12/10=6/5 и 0,48=48/100=12/25. Тогда деление десятичных дробей 1,2 и 0,48 можно свести к делению обыкновенных дробей 6/5 и 12/25. Итак, . Теперь можно , и записать ответ в виде смешанного числа , а можно полученную дробь 5/2 записать в виде десятичной дроби 2,5 (смотрите ).

Ответ:

1,2:0,48=2,5.

Пример.

Разделите периодическую десятичную дробь 0,(504) на десятичную дробь 0,56.

Решение.

: . Также переведем конечную десятичную дробь 0,56 в обыкновенную, имеем 0,56=56/100. Теперь мы можем перейти от деления исходных десятичных дробей к делению обыкновенных дробей и закончить вычисления: .

Переведем полученную обыкновенную дробь в десятичную дробь, выполнив деление числителя на знаменатель столбиком: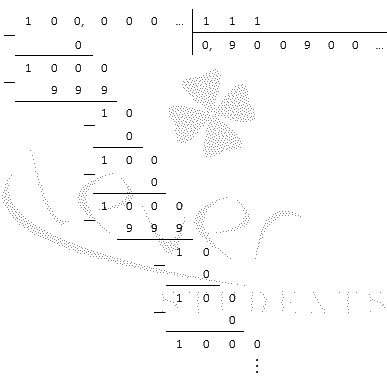

Ответ:

0,(504):0,56=0,(900).

Принцип деления бесконечных непериодических десятичных дробей отличается от принципа деления конечных и периодических десятичных дробей, так как непериодические десятичные дроби не могут быть переведены в обыкновенные дроби. Деление бесконечных непериодических десятичных дробей сводится к делению конечных десятичных дробей, для чего проводится округление чисел до некоторого разряда. Причем, если одним из чисел, с которыми проводится деление, является конечная или периодическая десятичная дробь, то она тоже округляются до того же разряда, что и непериодическая десятичная дробь.

Пример.

Разделите бесконечную непериодическую десятичную дробь 0,779… на конечную десятичную дробь 1,5602.

Решение.

Сначала нужно округлить десятичные дроби, чтобы от деления бесконечной непериодической десятичной дроби перейти к делению конечных десятичных дробей. Мы можем провести округление до сотых: 0,779…≈0,78 и 1,5602≈1,56. Таким образом, 0,779…:1,5602≈0,78:1,56=78/100:156/100=78/100·100/156=78/156=1/2=0,5.

Ответ:

0,779…:1,5602≈0,5.

Деление десятичной дроби на десятичную дробь

Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.

Например, разделим 5,95 на 1,7

Запишем уголком данное выражение

Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:

После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:

Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?

Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.

Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:

(9 × 2
) : (3 × 2
) = 18: 6 = 3

Как видно из примера, частное не поменялось.

Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.

На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:

5,91 × 10 = 59,1

Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.

Перенос запятой при делении на десятичную дробь

Хорошо, а что делать, если количество знаков после запятой в делимом и делителе разное? Например, если после переноса запятой делимое остаётся дробью?

Ничего страшного, делим дробь на натуральное число. Помните, что в этом случае нужно будет поставить в частном запятую, как только закончим делить целую часть делителя.

Например, разделим $7.04$ на $2.2$

Рисунок 5

Показать вычисления

Скрыть

Этот пример можно решить устно, не в столбик. $70$ делим на $22$, получается $3$ и $4$ в остатке. Ставим запятую после тройки, добавляем к $4$ число десятых – $4$. Теперь мы делим $44$ на $22$, у нас получается $2$.

$$7.04 : 2.2 = 3.2$$

Иногда бывает так, что знаков «не хватает». Например, нам нужно разделить 4.8 на 0.006. Как думаете, что нужно сделать в таком случае?

Показать ответ

Скрыть

Нужно дописать к делимому столько нулей, на сколько знаков нужно было бы перенести запятую.

Другими словами, мы всё равно умножаем и делимое, и делитель на одно и то же разрядное число. Если при этом приходится дописывать нули, это не делает наше вычисление ошибочным. Наоборот, если мы их не допишем, то разрядность «поедет», и ответ будет неверным.

Рисунок 6

{"questions":,"explanations":,"answer":}}}]}

Итак, деление на десятичную дробь почти не отличается от тех вычислений, что мы делали ранее

Важно только каждый раз переделывать делитель в натуральное число, умножая на разрядную единицу, и умножать делимое на то же самое разрядное число

{"questions":}},"step":1,"hints":["Вычислим значение $x$ в примере $86.4 : x = 43.2$<br />Чтобы найти делитель, нужно делимое разделить на частное. <br />$x = 86.4 : 43.2 = 864 : 432 = 2$","Вычислим значение $x$ в примере $x \\cdot 2.3 = 6.9$<br />Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. <br />$x = 6.9 : 2.3 = 69 : 23 = 3$","Вычислим значение $x$ в примере $53.4 : x = 5.34$<br />Чтобы найти делитель, нужно делимое разделить на частное. <br />$x = 53.4 : 5.34 = 5340 : 534 = 10$"]},{"content":"Соедините по парам части равенств, где $N$ и $M$ означают любые числа в пределах от $1$ до $9$. `matcher-10`","widgets":{"matcher-10":{"type":"matcher","labels":,"items":}},"step":1,"hints":["Чтобы выполнить деление на десятичную дробь, нужно умножить делимое и делитель на одну и те же разрядную единицу таким образом, чтобы делитель стал натуральным числом. <br />$0.0N : 0.M \t= (0.0N \\cdot 10) : (0.M \\cdot 10) = 0.N : M$","$0.N : 0.0M = (0.N \\cdot 100) : (0.0M \\cdot 100) =\tN0 : M$","$0.N : 0.M = (0.N \\cdot 10) : (0.M \\cdot 10) = N : M$"]},{"content":"Поезд прошёл $78$ километров за $1.3$ часа. Сколько километров он пройдёт за $2.4$ часа? `input-33`","widgets":{"input-33":{"type":"input","answer":"144"}},"step":1,"hints":["Для начала найдём скорость поезда. Для этого разделим расстояние, пройденное поездом, на время. У нас получится $78 : 1.3 = 780 : 13 = 60$","Теперь, зная скорость поезда – $60$ км/ч – мы можем легко посчитать, сколько он пройдёт за заданное время. <br />$60 \\cdot 2.4 = 144$"]}]}

Основы деления десятичных дробей

Десятичные дроби — это дроби, у которых в знаменателе стоят числа, кратные 10. То есть 10, 100, 1000 и так далее.

Как делить десятичные дроби друг на друга — процесс представляет собой деление обыкновенных дробей. То есть для выполнения действий деления мы переписываем десятичную дробь в стандартный вид.

Рассмотрим пример: разделите 1,2 на 0,6

Как решаем

Запишем десятичные дроби в виде обыкновенных. У нас получится:

Таким образом, нам надо разделить

Ответ: 1,2÷0,6 = 2

Если для деления нам попадается периодические и непериодические дроби, то действуем следующим образом.

Периодические переводим в обыкновенную:

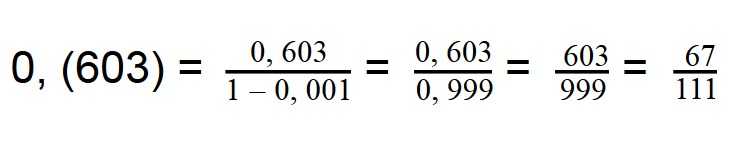
Если же встречается непериодическая десятичная дробь, то мы ее округляем до сотых и дальше делим, как обычно:

Деление десятичных дробей: основы, правила, примеры для тренировок

Примеры с дробями на деление

Десятичные дроби имеют в знаменателе числа, которые делятся на 10. Это 10, 100, 1000 и подобные им суммы.

Вот примеры для тренировок:

Примеры с дробями на деление
Примеры с дробями на деление
Примеры с дробями на деление
Примеры с дробями на деление

Бывает, что в примере на деление появляются определенные десятичные дроби непериодического свойства. Тогда тактика радикально меняется. К «привычному» виду их, как правило, привести нельзя.

Примеры с дробями на деление

Поэтому необходимо прибегать к логичному округлению. Это основы деления дробей. Производится округление до определенного разряда. Действие может быть применено как по отношению к делителю, так и по отношению к делимому. Это хорошо видно на примере выше.

Округлять нужно и конечную дробь, для точности и удобства. Но, на самом деле, в операциях с дробями данного вида нет ничего неординарного или затруднительного — все просто.

Смешанная дробь

То, что у нас получилось (\( \displaystyle  5\frac{2}{3}\)), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

То, что между \( \displaystyle  5\) пирогами и \( \displaystyle  2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle  2x\)!!!

Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle  5\frac{2}{3}=5+\frac{2}{3}\).

Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.

Ты же знаешь, как это сделать?

Преобразование из смешанной дроби в неправильную дробь.

Конечно, нужно умножить знаменатель дроби (в случае с , \(\displaystyle5\frac{2}{3}\) знаменатель равен \( \displaystyle  3\)), умножить знаменатель…, верно, на \(\displaystyle5\) и прибавить нецелую часть, а именно – \( \displaystyle  2\) .

Как разделить число на десятичную дробь

Бывают дроби другого вида – десятичные. Деление на них происходит по совсем другому алгоритму. Если вы столкнулись с таким примером, то придерживайтесь инструкции:

• Для начала, превратите оба числа в десятичные дроби. Сделать это просто: делитель у вас и так представлен в виде дроби, а делимое натуральное число вы отделяете запятой, получая десятичную дробь. То есть, если делимое было числом 5, вы получаете дробь 5,0. Отделять число нужно на столько цифр, сколько стоит после запятой и делителя.
• После этого, обе десятичные дроби вы должны сделать натуральными числами. Сперва, вам покажется это немного запутанным, но это самый быстрый способ деления, который будет занимать у вас секунды, после нескольких тренировок. Дробь 5,0 станет числом 50, дробь 6,23 будет 623.
• Выполните деление. Если числа получились большие, либо деление будет происходить с остатком, выполните его в столбик. Так вы наглядно увидите все действия данного примера. Вам не нужно специально ставить запятую, так как она сама появится в процессе деления в столбик.

Данный вид деления изначально кажется слишком запутанным, так как вам нужно превратить делимое и делитель в дробь, а потом снова в натуральные числа. Но после недолгой тренировки, вы сразу станете видеть те числа, которые нужно просто разделить друг на друга.

Помните, что умение правильно делить дроби и целые числа на них могут ни раз пригодиться в жизни, поэтому, знать эти правила и простые принципы ребенку нужно идеально, чтобы в более старших классах они не стали камнем преткновения, из-за которого ребенок не может решать более сложные задачи.

I.
Чтобы разделить десятичную дробь на натуральное число, нужно делить дробь на это число, как делят натуральные числа и поставить в частном запятую тогда, когда закончится деление целой части.

Примеры.

Выполнить деление
: 1)
96,25 5; 2)
4,78 4; 3)
183,06 45.

Решение.

Пример
1)
96,25 5.

Делим «уголком» так, как делят натуральные числа. После того, как сносим цифру 2

(число десятых — первая цифра после запятой в записи делимого 96,2

5), в частном ставим запятую и продолжаем деление.

Ответ
: 19,25.

Пример
2)
4,78 4.

Делим так, как делят натуральные числа. В частном поставим запятую сразу, как снесем 7

— первую цифру после запятой в делимом 4,7

8. Продолжаем деление дальше. При вычитании 38-36 получаем 2, но деление не окончено. Как поступаем? Мы знаем, что в конце десятичной дроби можно приписывать нули — от этого значение дроби не изменится. Приписываем нуль и делим 20 на 4. Получаем 5 — деление окончено.

Ответ
: 1,195.

Пример 3)
183,06 45.

Делим как 18306 на 45. В частном поставим запятую как только снесем цифру — первую цифру после запятой в делимом 183, 6. Так же, как в примере 2) нам пришлось приписать нуль к числу 36 — разности чисел 306 и 270.

Ответ
: 4,068.

Вывод
: при делении десятичной дроби на натуральное число в частном ставим запятую
сразу после того, как сносим цифру в разряде десятых делимого

Обратите внимание: все выделенные красным цветом цифры

в этих трех примерах относятся к разряду десятых
долей делимого.. II

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.

II
. Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д. нужно перенести запятую влево на 1, 2, 3 и т. д. цифр.

Примеры.

Выполнить деление: 1)
41,56 10; 2)
123,45 100; 3)
0,47 100; 4)
8,5 1000; 5)
631,2 10000.

Решение.

Перенос запятой влево зависит от того, сколько в делителе нулей после единицы. Так, при делении десятичной дроби на 10
мы будем переносить в делимом запятую влево на одну цифру
; при делении на 100

— перенесем запятую влево на две
цифры

; при делении на 1000

перенесем в данной десятичной дроби запятую на три цифры влево.

Как делить десятичную дробь на целое число?

Целые числа — это натуральные числа, числа им противоположные и ноль (… -2, -1, 0, 1, 2 …). Из определения целого числа, нетрудно догадаться, что в целом алгоритмы деления будут аналогичны алгоритма деления натурального числа на десятичную дробь. Таким образом:

1. Производим вычисления аналогично натуральным числам;
2. В случае если присутствует знак следуем следующим правилам:
   • Минус разделить на минус получится плюс;
   • Минус разделить на плюс получится минус;
   • Плюс разделить на минус получится минус.
3. В ответе ставим нужный знак.

Пример 4: Разделить 100 на -2,5.

Производим вычисления, по алгоритму деления натурального числа на десятичную дробь, не обращая внимания на знаки (чтобы не запутаться знаки можно не писать):

Из правила следует, что плюс разделить на минус будет минус, таким образом:

Ответ: 100 : (-2.5) = -40

Сокращение алгебраической дроби

Так же, как и в примерах выше, сокращение алгебраической дроби, это деление числителя и знаменателя на общий делитель. Отличие в том, что в алгебраической, таким общим множителем является многочлен и одночлен.

Для того чтобы сократить такие дроби нужно пройти три этапа:

• Определение множителя, который будет общим для числителя и знаменателя;
• Сокращение коэффициента;
• Деление числителя и знаменателя на множитель.

Сокращая дробь со степенями, применяется правило деления степеней с равными основаниями.

Формула:

Рассмотрим пример сокращения со степенями:

[ frac{x^{3}}{x^{2}}=frac{x^{3} / x^{2}}{x^{2} / x^{2}}=frac{x^{3-2}}{x^{2-2}}=frac{x^{1}}{x^{0}}=frac{x}{1}=x ]

Исходя из вышеописанной схемы:

• Сокращаем x3 и x2;
• Производим деление выбирая меньшее значение степени;
• Вычитаем.

В результате получаем сокращенную дробь.

Не забываем, что сократить можно только одинаковые буквенные множители.

Сокращение дробей с одночленами.

Пример

Решение:

8 — тот самый множитель, который является общим

Х и x2 делим на x и получаем ответ.

Дроби с многочленами: сокращение.

Для сокращения таких видов, существует два правила:

• Сократить многочлен в взятый в скобки, можно только с точно таким же многочленом в скобках;
• Сократится должен весь многочлен, взятый в скобки, нельзя сократить только часть.

Пример:

Вынесение общего множителя при сокращении.

Бывают случаи, когда при сокращении алгебраической дроби с многочленами, их нет одинаковых, в таком случае нужно убрать общий множитель за скобки.

Для такого вынесения тоже существуют правила их 4:

1. необходимо найти число, на которое можно разделить числа каждого одночлена;
2. необходимо также найти буквенный множитель, который повторяется, в каждом одночлене, их может быть несколько;
3. выносим буквенный множитель, который был найден, за скобки;
4. производим работу с оставшимися многочленами в скобках.

Для того чтобы умножить многочлен на одночлен, необходимо по очереди умножить каждый член многочлена на одночлен.

Приведём пример:

Деление с дробными числами

С дробными числами все обстоит примерно также. Главная проблема – это страх перед дробями. Если поделить целое число на дробное не кажется большой проблемой, то вот при делении дроби на дробь почему-то на учеников нападает иррациональный страх.

Чтобы его не было просто перенесите запятую.

$3,8:0,5=38:5$ – а дальше в действие вступают правила деления без остатка.

$$3,8:0,5=38:5=7,6$$

Если вдруг необходимый результат нужно записать в виде дроби, то процесс упрощается еще больше. В результате преобразований делимое переместится в числитель, а делитель в знаменатель. Смотрите внимательно за преобразованиями и не теряйте запятых:

$$3,5:1,8={35\over{10}}:{18\over{10}}={{35*10}\over{18*10}}={35\over{18}}$$ – вот и весь расчет. Иногда приходится применять деление десятичных дробей в столбик. В этом случае, проще всего также воспользоваться этим методом.

Полезные советы и выводы

• В некоторых случаях может потребоваться использовать вспомогательные устройства, такие как калькулятор, для более сложного деления.
• При работе с десятичными дробями необходимо быть внимательными и аккуратными, так как малейшая ошибка может привести к неверным результатам.
• Перевод обыкновенной дроби в десятичную форму является важным навыком и может пригодиться в повседневной жизни, особенно при финансовых расчетах.

В этой статье мы рассмотрели различные способы преобразования обыкновенной дроби в десятичную. Надеемся, что эта информация окажется полезной и поможет вам лучше разобраться в этом математическом процессе.

Что нужно сделать чтобы разделить десятичную дробь на 100

Чтобы разделить десятичную дробь на 100, нужно передвинуть запятую на две позиции влево. Например, если у нас есть число 347,3 и мы хотим разделить его на 100, то переносим запятую на две цифры влево и получаем 3,473. То есть результатом этого деления будет число 3,473. Точно так же можно разделить любую другую десятичную дробь на 100. Например, если у нас есть число 1078,42 и мы хотим разделить его на 100, то переносим запятую на две цифры влево и получаем 10,7842. Таким образом, результатом этого деления будет число 10,7842. В обоих случаях мы разделили исходные десятичные дроби на 100 путем перемещения запятой влево.

Как десятичную дробь умножать на 100

Например, если у нас есть десятичная дробь 0,25, и мы хотим умножить ее на 100, то запятую нужно перенести вправо на два знака: получится 25. То есть 0,25 * 100 = 25. Если бы мы хотели умножить эту дробь на 1000, то запятую нужно было бы перенести вправо на три знака, и результат был бы 250.

Таким же образом можно умножать и на 10. Например, если у нас есть десятичная дробь 0,05, и мы хотим умножить ее на 10, то запятую нужно перенести вправо на один знак: получится 0,5. То есть 0,05 * 10 = 0,5.

Помни, что умножая десятичную дробь на 100, 1000 и т.д., мы увеличиваем ее в разы.

Как перевести десятичную дробь в целую

1. Упрощаем полученную дробь. Для этого делим числитель и знаменатель на их наибольший общий делитель. После упрощения дроби получаем итоговое значение.

Например, рассмотрим дробь 0,25. Сначала перепишем ее в виде обыкновенной дроби: 25/100. Затем умножим числитель и знаменатель на 10: 250/1000. Далее упростим дробь: делим числитель и знаменатель на 10 и получаем 25/100. Находим их наибольший общий делитель, который равен 25. Делим числитель и знаменатель на этот делитель и получаем итоговое значение: 1/4.

Таким образом, десятичная дробь 0,25 равна обыкновенной дроби 1/4.

Как разделить обыкновенную дробь на обыкновенную дробь

Далее приводим новую дробь к несократимому виду, если это возможно. Для этого находим наименьшее общее кратное (НОК) знаменателей новой дроби и сокращаем числитель и знаменатель новой дроби на это НОК.

Например, разделим дробь 3/4 на дробь 2/3. Умножаем числитель первой дроби (3) на знаменатель второй (3), получаем 9. Умножаем знаменатель первой дроби (4) на числитель второй (2), получаем 8. Полученная дробь будет 9/8, которую можно сократить на наименьшее общее кратное знаменателей (8). Делаем сокращение и получаем несократимую дробь 9/8.

Таким образом, обыкновенную дробь можно разделить на другую обыкновенную дробь, выполнив указанные операции.