Округление с избытком и недостатком
Почему мы сравниваем именно с $5$?
Потому что именно $5$ десятых равно удалено и от меньшего числа, и от большего.
Позже Образавр купил другие весы, чтобы взвесить арбуз точнее, и узнал, что он весит $4.8$ кг.
Так как масса арбуза почти равна $5$, то можно сказать, что его массу можно округлить до $5$ кг.
А что же делать, если у числа ровно $5$ десятых? Например, кот Рыжик весит ровно $6,5$ кг. Число $6,5$ равно удалено и от $6$ кг, и от $7$ кг. Если мы хотим округлить массу Рыжика до целых, то чему она будет равна?
Следовательно, массу Рыжика также нужно будет округлить с избытком, и она будет приближённо равна $7$ кг.
{"questions":,"items":,]}},"step":1,"hints":}]}
Правило встречается в следующих упражнениях:
5 класс
Задание 1273,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1470,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1557,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 449,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 844,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 855,
Мерзляк, Полонский, Якир, Учебник
Номер 858,
Мерзляк, Полонский, Якир, Учебник
Номер 1036,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 563,
Мерзляк, Полонский, Якир, Учебник
Номер 571,
Мерзляк, Полонский, Якир, Учебник
Номер 645,
Мерзляк, Полонский, Якир, Учебник
Номер 747,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Задание 645,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 740,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1198,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1223,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1580,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 150,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 265,
Мерзляк, Полонский, Якир, Учебник
Номер 295,
Мерзляк, Полонский, Якир, Учебник
Номер 297,
Мерзляк, Полонский, Якир, Учебник
Номер 385,
Мерзляк, Полонский, Якир, Учебник
Номер 386,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Операции с десятичными дробями
Дробь включает целую и дробную части. Первая округляется аналогично натуральным числам. В случае со второй отбрасываемые цифры не просто заменяются нулём, а убираются.
Например, необходимо округлить дробь 3,284 до целых. Это обозначает, что стоя́щие после запятой цифры нужно «удалить». Решение:
- Начинать следует с конца. В разряде тысячных указана 4. Она меньше 5, поэтому цифра отбрасывается, а остальное не меняется: 3,284≈3,28.
- А вот число 8 больше 5. Цифра 2, что идёт перед ней, увеличивается на единицу. Так число округляется до десятых 3,28≈3,3.
- Последнее вычисление делается по аналогии. Так как 3<5, то 3,3≈3.
- Конечный ответ — 3,284≈3.
https://youtube.com/watch?v=U7lxssUChMc
Правила округления
Для получения приближённого значения, полученное в результате каких-либо действий число нужно округлить, то есть заменить его ближайшим круглым числом.
Числа всегда округляют до определённого разряда. Натуральные числа округляются до десятков, сотен, тысяч и т. д. При округлении чисел до десятков, их заменяют круглыми числами, состоящими только из целых десятков, у таких чисел в разряде единиц стоят нули. При округлении до сотен, числа заменяются на более круглые, состоящие только из целых сотен, то есть нули стоят уже и в разряде единиц, и в разряде десятков. И так далее.
Десятичные дроби можно округлять так же как и натуральные числа, то есть до десятков, сотен и т. д. Но также их можно округлять и до десятых, сотых, тысячных частей и т. д. При округлении десятичных знаков разряды не заполняются нулями, а просто отбрасываются. В обоих случаях округление производится по определённому правилу:
Если отбрасываемая цифра больше или равна 5, то предыдущую нужно увеличить на единицу, а если меньше 5, то предыдущая цифра не меняется.
Рассмотрим несколько примеров округления чисел:
- Округлить 43152 до тысяч. Здесь надо отбросить 152 единицы, так как справа от разряда тысяч стоит цифра 1, то предыдущую цифру отставляем без изменений. Приближённое значение числа 43152, округлённое до тысяч будет равно 43000.
- Округлить 43152 до сотен. Первая из отбрасываемых чисел 5, значит предыдущую цифру увеличиваем на единицу: 43152 ≈ 43200.
- Округлить 43152 до десятков: 43152 ≈ 43150.
- Округлить 17,7438 до единиц: 17,7438 ≈ 18.
- Округлить 17,7438 до десятых: 17,7438 ≈ 17,7.
- Округлить 17,7438 до сотых: 17,7438 ≈ 17,74.
- Округлить 17,7438 до тысячных: 17,7438 ≈ 17,744.
Знак ≈ называют знаком приближённого равенства, он читается — «приближённо равно».
Если при округлении числа результат получился больше начального значения, то полученное значение называется приближённым значением с избытком
, если меньше — приближённым значением с недостатком
:
7928 ≈ 8000, число 8000 — приближённое значением с избытком
5102 ≈ 5000, число 5000 — приближённое значением с недостатком
Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4,
то подчеркнутую цифру оставляем без изменения
. Если первая замененная нулем или отброшенная цифра равна 5, 6, 7, 8 или 9,
то подчеркнутую цифру увеличиваем на 1.
Примеры.
Округлить до целых:
1)
12,5; 2)
28,49; 3)
0,672; 4)
547,96; 5)
3,71.
Решение.
Подчеркиваем цифру, стоящую в разряде единиц (целых) и смотрим на цифру, стоящую за ней. Если это цифра 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения, а все цифры после нее отбрасываем. Если же за подчеркнутой цифрой стоит цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на единицу.
1)
12
,5≈13;
2)
28
,49≈28;
3)
0
,672≈1;
4)
547
,96≈548;
5)
3
,71≈4.
Округлить до десятых:
6)
0, 246; 7)
41,253; ![]()
3,81; 9)
123,4567; 10)
18,962.
Решение.
Подчеркиваем цифру, стоящую в разряде десятых, а затем поступаем согласно правилу: все стоящие после подчеркнутой цифры отбросим. Если за подчеркнутой цифрой была цифра 0 или 1 или 2 или 3 или 4, то подчеркнутую цифру не изменяем. Если за подчеркнутой цифрой шла цифра 5 или 6 или 7 или 8 или 9, то подчеркнутую цифру увеличим на 1.
6)
0, 2
46≈0,2;
7)
41,2
53≈41,3;
![]()
3,8
1≈3,8;
9)
123,4
567≈123,5;
10)
18,9
62≈19,0. За девяткой стоит шестерка, поэтому, девятку увеличиваем на 1. (9+1=10) нуль пишем, 1 переходит в следующий разряд и будет 19. Просто 19 мы в ответе записать не можем, так как должно быть понятно, что мы округляли до десятых — цифра в разряде десятых должна быть. Поэтому, ответ: 19,0.
Округлить до сотых:
11)
2, 045; 12)
32,093; 13)
0, 7689; 14)
543, 008; 15)
67, 382.
Решение.
Подчеркиваем цифру в разряде сотых и, в зависимости от того, какая цифра стоит после подчеркнутой, оставляем подчеркнутую цифру без изменения (если за ней 0, 1, 2, 3 или 4) или увеличиваем подчеркнутую цифру на 1 (если за ней стоит 5, 6, 7, 8 или 9).
11)
2, 04
5≈2,05;
12)
32,09
3≈32,09;
13)
0, 76
89≈0,77;
14)
543, 00
8≈543,01;
15)
67, 38
2≈67,38.
Важно:
в ответе последней должна стоять цифра в том разряде, до которого вы округляли
Формула округление
Одна из часто применяемых функций округления – ОКРУГЛ
. Она работает по стандартным математическим правилам. Выбираем ячейку, щелкаем значок «Вставить функцию
», категория «Математические
», находим ОКРУГЛ
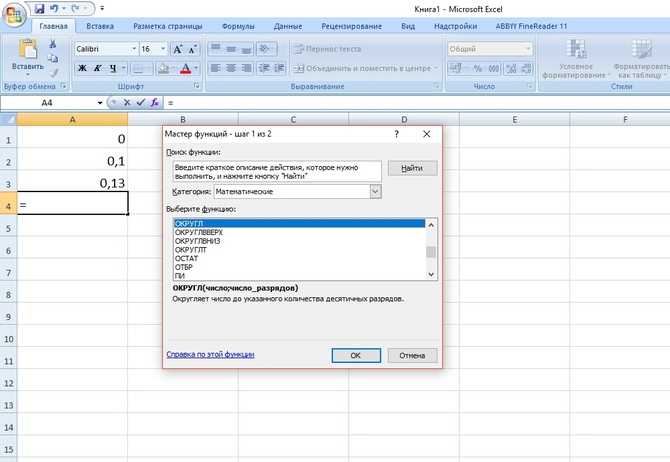
Определяем аргументы, их два – сама дробь
и количество
разрядов. Щелкаем «ОК
» и смотрим, что получилось.
К примеру, выражение =ОКРУГЛ(0,129;1)
даст результат 0,1. Нулевое количество разрядов позволяет избавляться от дробной части. Выбор отрицательного количества разрядов позволяет округлять целую часть до десятков, сотен и так далее. Например, выражение =ОКРУГЛ(5,129;-1)
даст 10.
Округление натуральных чисел
Когда полная точность не нужна или невозможна, числа округляют, т.е. заменяют близкими числами с нулями на конце. Например, на концерт продано 9 678 билетов, данное число в разговоре можно заменить выражением «около 10 тыс. билетов». В таком случае число 10 тыс. называют приближенным значением числа 9 678 и говорят, что число 9 678 округлили до числа 10 тыс. Записывают 9 67810 тыс.
В зависимости от ситуации натуральные числа округляют до того или иного разряда: до десятков, до сотен, до тысяч и т.д.
Правило округления натуральных чисел
|
Примеры:
а) Округлим до сотен тысяч число 1 456 345.
Подчеркиваем цифру в разряде сотен тысяч 1 456 345. Справа от подчеркнутой цифры стоит 5, поэтому прибавляем к цифре подчеркнутого разряда 1 и заменяем нулями все цифры, расположенные справа от подчеркнутой, получим 1 500 000.
Записывают решение так: 1 456 3451 500 0001 млн 500 тыс.
б) Округлим до миллионов число 32 123 574.
Подчеркиваем цифру в разряде миллионов 32 123 574. Справа от подчеркнутой цифры стоит 1, поэтому цифру подчеркнутого разряда оставляем ту же и заменяем нулями все цифры, расположенные справа от подчеркнутой, получим 32 000 000.
Записывают решение так: 32 123 57432 000 00032 млн.
Обратите внимание: в круглом числе должно получится столько же цифр, как и в исходном. Если мы число округляем в большую сторону (т.е
прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с избытком, если же округляем число в меньшую сторону (т.е. не прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с недостатком
Если мы число округляем в большую сторону (т.е. прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с избытком, если же округляем число в меньшую сторону (т.е. не прибавляем к округляемой цифре разряда 1), тогда такое число называют приближенным значением с недостатком.
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
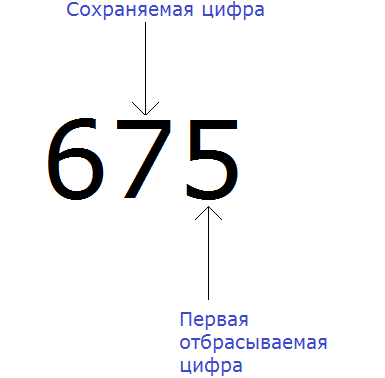
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой
.

У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен
.
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3.
Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4.
Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5.
Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6.
Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
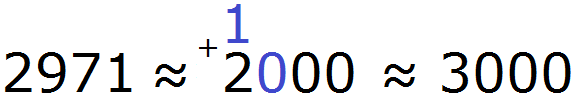
2971 ≈ 3000
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3. Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4. Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5. Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6. Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
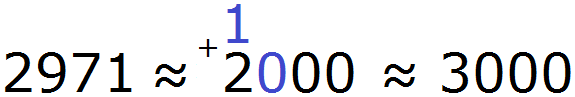
2971 ≈ 3000
Главное правило
Основной принцип, который нам необходимо усвоить — это то, как заменять цифры при округлении. Дело все в том, что сделать это довольно легко. Давайте посмотрим, как именно.
Если в качестве цифры разряда у вас 0, 1, 2, 3 или 4, то она автоматически заменяется на 0 и отбрасывается. Далее двигаемся ближе к целой части и смотрим на следующее число.
Как только цифра в разряде будет равна 5, 6, 7, 8 или 9, вам придется отбросить эту часть, а к следующему (ближнему к целой части) числу следует прибавить одну единицу. Данный процесс необходимо повторять вплоть до выбранной нами точности округления. Давайте теперь посмотрим с вами пример. На нем все будет выглядеть понятнее.
Округление чисел с помощью функций
Для округления фактических значений в ячейках можно использовать функции ОКРУГЛ , ОКРУГЛВВЕРХ , ОКРУГЛВНИЗ и ОКРУГЛТ , как показано в следующих примерах.
Округление числа до ближайшего значения
В этом примере показано, как округлить число до ближайшего значения с помощью функции ОКРУГЛ .
При округлении числа формат ячейки может переопределять отображаемый результат. Например, если во втором аргументе указано 4 десятичных разряда, но в формате ячейки задано отображение 2 чисел после запятой, будет применяться формат ячейки.
Округление числа вверх
функцию ОКРУГЛВВЕРХ .
Вы также можете использовать функции ЧЁТН и НЕЧЁТ для округления значения вверх до ближайшего четного или нечетного целого числа
Область применения этих функций ограничена, и важно помнить о том, что они всегда округляют число вверх и только до целого числа
Округление числа до указанного количества значимых разрядов
В этом примере показано, как округлить число до определенного количества значимых разрядов. Значимые разряды — это разряды, которые влияют на точность числа.
В списке ниже приведены общие правила, которые необходимо учитывать при округлении чисел до указанного количества значимых разрядов. Вы можете поэкспериментировать с функциями округления и подставить собственные числа и параметры, чтобы получить значение с нужным количеством разрядов.
При использовании функции ОКРУГЛ число округляется вверх, если его дробная часть равна 0,5 или больше этого значения. Если она меньше, число округляется вниз. Целые числа также округляются вверх или вниз согласно аналогичному правилу (при этом проверяется, не меньше ли 5 последняя цифра числа).
В общем при округлении целого числа необходимо вычесть длину числа из нужного количества значимых разрядов. Например, чтобы округлить 2345678 вниз до 3 значимых разрядов, используется функция ОКРУГЛВНИЗ с параметром -4. Так,= ОКРУГЛВНИЗ(2345678;-4)
округляет число до значения 2340000, где часть «234» представляет собой значимые разряды.
Для округления отрицательное число, то же число сначала преобразуется в его абсолютное значение — значением без знак «минус». По завершении округление повторно применяется знак «минус». Например при использовании ОКРУГЛВНИЗ для округления -889
для двух результатов значащих цифр в -880
-889
преобразуется в 889
и округляется вниз до 880
. Знак «минус» затем повторно для конечный результат -880
.
Округление числа до заданного кратного
Иногда бывает нужно округлить число до кратного. Например, если ваша компания поставляет товары в ящиках по 18 единиц, вам может потребоваться узнать, сколько ящиков нужно для поставки 204 единиц. Функция ОКРУГЛТ делит число на нужное кратное, а затем округляет результат. В данном случае ответом является 12, так как при делении 204 на 18 получается значение 11,333, которое округляется до 12 из-за наличия остатка. В 12-м ящике будет только 6 единиц товара.
В этом примере показано, как использовать функцию ОКРУГЛТ для округления числа до заданного кратного.
Примечание:
Отказ от ответственности относительно машинного перевода
. Данная статья была переведена с помощью компьютерной системы без участия человека. Microsoft предлагает эти машинные переводы, чтобы помочь пользователям, которые не знают английского языка, ознакомиться с материалами о продуктах, услугах и технологиях Microsoft. Поскольку статья была переведена с использованием машинного перевода, она может содержать лексические,синтаксические и грамматические ошибки.
На предыдущей странице мы обсудили, как округлить натуральное число. Теперь рассмотрим, как
округлить десятичную дробь
.
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных
и т.д.
Важно помнить и не путать названия разрядов до и после запятой в десятичной дроби
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин, иногда можно использовать приближенные значения.
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды
Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых
Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной
Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?Используй кнопку ниже
![]()
![]()
Круглое число
Перед тем как перейти к правилам округления значений, стоит разобраться, что представляет собой круглое число
. Если речь идет о целых, то оно обязательно заканчивается нулем.
На вопрос, где в повседневной жизни пригодиться такое умение, можно смело ответить – при элементарных походах по магазинам.
С помощью правила приблизительного подсчета можно прикинуть, сколько будут стоить покупки и какую сумму необходимо взять с собой.
Именно с круглыми числами легче выполнять подсчеты, не используя при этом калькулятор.
К примеру, если в супермаркете или на рынке покупают овощи весом 2 кг 750 г, то в простом разговоре с собеседником зачастую не называют точный вес, а говорят, что приобрели 3 кг овощей. При определении расстояния между населенными пунктами также применяют слово «около». Это и значит приведение результата к удобному виду.
Следует отметить, что при некоторых подсчетах в математике и решении задач также не всегда используются точные значения. Особенно это актуально в тех случаях, когда в ответе получают бесконечную периодическую дробь
. Приведем несколько примеров, когда используются приближенные значения:
- некоторые значения постоянных величин представляются в округленном виде (число «пи» и прочее);
- табличные значения синуса, косинуса, тангенса, котангенса, которые округлены до определенного разряда.
Обратите внимание!
Как показывает практика, приближение значений к целому, конечно, дает погрешность, но сосем незначительную. Чем выше разряд, тем точнее будет результат






























