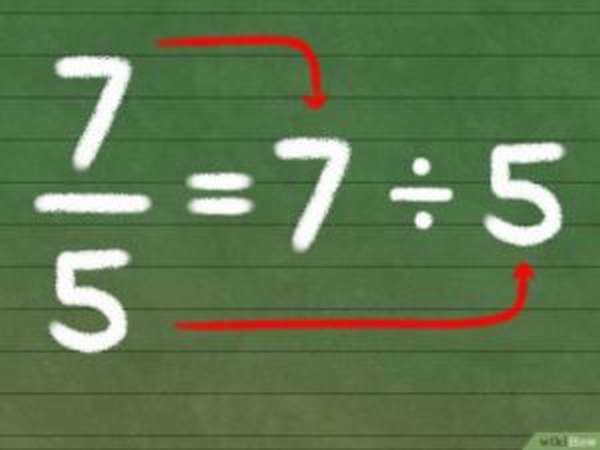Основное свойство дроби. сокращение дробей

Как использовать сокращение дробей в повседневной жизни

Сокращение дробей может быть полезным навыком, который вы можете использовать в повседневной жизни. Например, когда вы готовите еду, возможно, вам нужно уменьшить количество ингредиентов по рецепту, и сокращение дробей позволяет делать это быстрее и легче.

Кроме того, вам может пригодиться сокращение дробей, когда вы делаете бюджет или планируете общие расходы. Если вам нужно разделить билль на какое-то количество людей, сокращенная дробь может сделать этот процесс более простым и точным.

Сокращение дробей также может пригодиться, когда вы изучаете математику или физику. Понимание, как сокращать дроби, может помочь вам решать уравнения и производить математические операции быстрее и без ошибок.

• Чтобы сократить дробь, найдите общий делитель числителя и знаменателя.
• Делите числитель и знаменатель на найденный общий делитель.
• Получившуюся дробь можно еще выразить в виде смешанной дроби или десятичной дроби для более удобного использования.

Не бойтесь использовать сокращение дробей в повседневной жизни. Это может помочь вам быть более организованным и точным, а также сэкономить время и силы. И запомните, практика делает мастера!

Как сократить дробь? Правило и примеры сокращения дробей

Осталось лишь разобрать правило сокращения дробей, которое и объясняет, как сократить данную дробь.

Правило сокращения дробей
состоит из двух шагов:

• во-первых, находится НОД числителя и знаменателя дроби;
• во-вторых, проводится деление числителя и знаменателя дроби на их НОД, что дает несократимую дробь, равную исходной.

Разберем пример сокращения дроби
по озвученному правилу.

Пример.

Сократите дробь 182/195
.

Решение.

Выполним оба шага, предписанные правилом сокращения дроби.

Сначала находим НОД(182, 195)
. Наиболее удобно воспользоваться алгоритмом Евклида (смотрите ): 195=182·1+13
, 182=13·14
, то есть, НОД(182, 195)=13
.

Теперь делим числитель и знаменатель дроби 182/195
на 13
, при этом получаем несократимую дробь 14/15
, которая равна исходной дроби. На этом сокращение дроби закончено.

Кратко решение можно записать так: .

Ответ:

На этом с сокращением дробей можно и закончить. Но для полноты картины рассмотрим еще два способа сокращения дробей, которые обычно применяются в легких случаях.

Иногда числитель и знаменатель сокращаемой дроби несложно . Сократить дробь в этом случае очень просто: нужно лишь убрать все общие множители из числителя и знаменателя.

Стоит отметить, что этот способ напрямую следует из правила сокращения дробей, так как произведение всех общих простых множителей числителя и знаменателя равно их наибольшему общему делителю.

Разберем решение примера.

Пример.

Сократите дробь 360/2 940
.

Решение.

Разложим числитель и знаменатель на простые множители: 360=2·2·2·3·3·5
и 2 940=2·2·3·5·7·7
. Таким образом, .

Теперь избавляемся от общих множителей в числителе и знаменателе, для удобства, их просто зачеркиваем: .

Наконец, перемножаем оставшиеся множители: , и сокращение дроби закончено.

Вот краткая запись решения: .

Ответ:

Рассмотрим еще один способ сокращения дроби, который состоит в последовательном сокращении. Здесь на каждом шаге проводится сокращение дроби на некоторый общий делитель числителя и знаменателя, который либо очевиден, либо легко определяется с помощью

Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.

Сократить дробь — значит, разделить числитель и знаменатель на одно и то же . И 360, и 420 оканчиваются на цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2. В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.

К этому же ответу можем прийти другим путем.

И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3. Пришли к результату — шесть седьмых.

И еще один вариант решения.

В следующий раз рассмотрим примеры сокращения дробей.

Возможно, будет полезно почитать:

• Йога для лица — описание комплекса упражнений для омоложения кожи ;
• Йога для омоложения организма ;
• Опасные упражнения в спортзале, которые стоит вычеркнуть из своей программы ;
• Skyrim: чит-коды оружия, навыков, брони и зaчарования Коды на скайрим эльфийские стрелы ;
• Классический подъем и ласточка ;
• Строение руки — иннервация ;
• Что такое, причины возникновения спастичности, недопущение и лечение Как убрать спастику после инсульта ;
• Способы как вызвать рвоту для похудения ;

Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)

Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.

Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если r_k+1=0, при этом r_k=НОД(a, b)

Пример. Рассчитаем НОД для 28 и 64.

Как находим:

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (28) = 2 * 2 * 7

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Примеры решения задач

Задача 1

Сократить дробь 5/15

Решение: НОД дроби \(5/15
\) является 3. Разделив на 3 числитель и знаменатель, получаем \(1/5\)

Задача 2

Провести сокращение дроби 56/8.

Первым шагом превратим смешанную дробь в неправильную: \(56/8=46/8=(2*23)/(2*4)=23/4=53/4\)

Задача 3

Сократить неправильную дробь 86/42.

Решение: \((43*2)/(21*2)=43/21\)

Задача 4

Сократив дроби, найти значение выражения: 6/9+12/36

Решение: \(6/9+12/36=(2*3)/(3*3)+(1*12)/(3*12)=2/3+1/3=3/3\)

Результат примеры — неправильная дробь, в которой числитель равен знаменателю. Следовательно, ответом является 1.

Основные понятия

Для того, чтобы понять, что это за значение такое, необходимо представить некий целый предмет. Допустим, что есть торт, который порезали на несколько одинаковых или равных кусков. Каждый кусочек будет называться долей.

Важно! В случае с дробями, есть некое целое число, которое состоит из равных долей – отдельных меньших чисел. Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти

Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти.

Доли имеют свои названия, в зависимости от их общего количества в целом числе: 10 может состоять из двух пятёрок или пяти двоек, в первом случае она будет называться  (одна вторая), а во втором  (одна пятая). Следует помнить, что   равняется половине числа,  (одна третья)  трети, а   (одна четвертая)  – четвертью. Их могут также изображать через черточку: ½, 1/3 или 1/5.

Цифру, написанную сверху горизонтальной линии или слева от наклонной, называют числителем – он показывает сколько долей взяли у целого числа, а цифра под линии или справа от нее – знаменатель, он показывает на сколько всего долей разделили. Например, торт разделили на 10 кусков и сразу отложили два из них для опоздавших гостей. Это будет 2/10 (две десятых), т.е. взяли 2 (числитель) куска от общих 10 (знаменатель).

Дроби

Какие бывают доли, что такое неправильная дробь, что такое обыкновенная дробь? На эти вопросы легко ответить:

1. Обыкновенная – это такая, в котором числитель и знаменатель являются натуральными числами и записываются так:  или m/n,
2. Правильная дробь – это такая, которая по своей величине меньше единицы, а числитель меньше знаменателя: 5/7 (пять седьмых), 3/5 (три пятых),
3. Неправильная – это такая, которая больше или равна единице, а ее знаменатель меньше или равен числителю: 7/5 (семь пятых) или 19/3 (девятнадцать третьих),
4. Смешанная – это состоящая из целого и доли: 2 (две целых три пятых) или 5 (пять целых шесть двенадцатых) .

Смешанная цифра всегда может трансформироваться в неправильную дробь и наоборот.

Главное свойство гласит: при умножении, а также деления делимого и делителя на одинаковый множитель, в целом величина дроби не изменится. Это свойство делает возможным все операции с дробями.

Как из неправильной дроби сделать правильную

Последовательность действий с дробями со степенями

Для того чтобы без проблем разобраться в вопросе о том, как сократить дробь со степенями, необходимо твердо запомнить основные действия с ними. Первое из них связано с умножением степеней. В этом случае, если основания одинаковые, показатели необходимо сложить.

Второе — деление. Опять же у тех, которые имеют одинаковые основания, показатели потребуется вычесть. Причем вычитать нужно из того числа, которое стоит в делимом, а не наоборот.

Третье — возведение в степень степени. В этой ситуации показатели перемножаются.

Для успешного сокращения потребуется также умение приводить степени к одинаковым основаниям. То есть видеть, что четыре — это два в квадрате. Или 27 — куб трех. Потому что сократить 9 в квадрате и 3 в кубе сложно. Но если преобразовать первое выражение как (3 2) 2 , то сокращение пройдет успешно.

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком
, и решение записывают в таком виде:
497: 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое
, 4 — делитель
.
Результат деления при делении с остатком называют неполным частным
. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток
.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело
. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенствоа = b * n + r ,

где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление
.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби
.

Два последних преобразования называют сокращением дроби
.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю
.

Виды дробей. Преобразования.

Дроби бывают трёх видов.

1. Обыкновенные дроби, например:

Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем, нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Зззззапомни! Зззззнаменатель — внизззззу!» Глядишь, всё и ззззапомнится.)

Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.

1/2 = 1 : 2

Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.

32/8 = 32 : 8 = 4

Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.

2. Десятичные дроби, например:

0,5 или 3,28 или 0,125 и так далее.

Именно в таком виде нужно будет записывать ответы на задания «В».

3. Смешанные числа, например:

Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.

Наиболее универсальны обыкновенные дроби. С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями!

Сравнение дробей

1. Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
2. Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
2. разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Приведение дробей к наименьшему общему знаменателю

Когда простые обыкновенные дроби, имеют одинаковые по значению знаменатели, то это характеризуется как дроби приведены к общему знаменателю.

Например: значения 45/₇₆ и 143/₇₆  приведены к общему знаменателю, числу 76. Рассмотрим еще несколько дробей. Рассмотрим еще несколько дробей 1/₃, 3/₃, 17/₃ и 1000/₃.

Все эти значения приведены к общему знаменателю 3.

В случае, если знаменатели дробных чисел, являются разными по значениям и не равны друг другу. Можно их привести к общему числовому знаменателю. Для этого значение числителя и знаменателя данных значений перемножим с дополнительным множителем.

Например: 2/₅ и 7/₄ — эти дроби имеют разные знаменатели, поэтому воспользуемся приведение к общему знаменателю, при помощи дополнительных множителей, а именно 4 и 5.

Применяя данные значения приведем и вычисления и получим общий множитель: значение равное 20. При перемножении числителя и знаменателя дроби  2/₅ на значение равное 4, получим дробь вида 8/₂₀. Проводим аналогичные действия, но только с дробью При перемножении числителя и знаменателя дроби  7/₄ на 5 и приведем ее к дроби вида 35/₂₀ .

Теперь можно сформулировать определение, приведение дробей к общему знаменателю.

Приведение дробей к знаменателю одинаковых значений – это вычислительный процесс, который включает в себя: умножение числителей и знаменателей любых значений дробей на определенные значения дополнительных множителей, чтобы результаты проведенных вычислений получились дроби с одинаковыми знаменателями.

В математике существует правило, которое помогает привести дроби к общему наименьшему знаменателю.

Данное правило включает в себя три основных пункта.

Принцип приведения дробного значения к наименьшему общему знаменателю:

• Для начала определяется значение наименьшего общего знаменателя дробей.
• Затем для каждой дроби определяется дополнительный множитель. Он должен соответствовать правилу: деление наименьшего общего знаменателя на знаменатель, каждой рассматриваемой при решении, дроби.
• Перемножаем числитель и знаменатель на принятый дополнительный множитель.

Примеры решения задач, используя приведение к наименьшему знаменателю.

Пример №1:

Нужно привести к наименьшему знаменателю следующие дроби: 5/₁₄ и 7/₁₈

Для решения применим алгоритм решения, рассмотренный в вышеприведенном пункте.

Для начала определим наименьшее значение общего знаменателя, который равен минимальному и кратному числу 14 и 18.

Разложим значения знаменателей на множители: 14=2*7, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=126. Следующим шагом, будет вычисление дополнительных множителей. С их помощью приведем дробные значения 5/₁₄ и 7/₁₈ будут приведены к числу 126. Дробному значению 5/₁₄ дополнительный множитель будет равняться 126/14=9. Для значения второй дроби равной 7/₁₈ аналогичный множитель будет равняться 129/18=7.

Числители и знаменатели дробей перемножаем на дополнительный множитель 9 и 7 соответственно.

Записываем следующие выражения:

\
\

Итоги проведенных вычислений: заданные дроби 5/₁₄ и 7/₁₈ приведены к общему знаменателю. Итоговое значение выражения: 45/₂₆ и 49/₁₂₆.

Пример №2:

Нужно привести к наименьшему знаменателю следующие дроби: 3/₁₂ и 5/₁₈. В этом примере, также применим алгоритм решения, состоящий из трех главным действий.

Используя алгоритм решения, определим наименьшее значение общего знаменателя, который равен самому минимальному значению и кратному числам 12 и 18.

Следующим шагом, разлом данные значения на множители: 12=2*6, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=216. Произведем вычисление дополнительных множителей. С их помощью приведем дробные значения 3/₁₂ и 5/₁₈ будут приведены к числу 216. Дробному значению 3/₁₂ дополнительный множитель будет равняться 216/12=18. Для значения второй дроби равной 7/₁₈ , аналогичный множитель будет равняться 216/18=12.

Данные значений дробей, нужно перемножить на дополнительный числовой множитель равный числам 9 и 7 соответственно. Подставим эти данные и вычислим составленные выражения.

Записываем следующие выражения:

\
\

Итоги проведенных вычислений: заданные дроби 5/₁₄ и 7/₁₈ не приведены к общему знаменателю. Окончательное  значение выражения 27/₁₀₈ и 35/₁₂₆ и из этого следует, что знаменатели разные.

Ответ: значение 216 не будет являться наименьшим общим знаменателем.

Аналогичным способом, используя алгоритм решения можно определить значение наименьшего знаменателя трех и более дробных значений.

Сокращение алгебраических дробей

Сокращение алгебраических (рациональных) дробей основано на их основном свойстве: если числитель и знаменатель дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Сокращать можно только множители!

Члены многочленов сокращать нельзя!

Чтобы сократить алгебраическую дробь, многочлены, стоящие в числителе и знаменателе, нужно предварительно разложить на множители.

Рассмотрим примеры сокращения дробей.

В числителе и знаменателе дроби стоят одночлены. Они представляют собой произведение (чисел, переменных и их степеней), множители сокращать можем.

Числа сокращаем на их наибольший общий делитель, то есть на наибольшее число, на которое делится каждое из данных чисел. Для 24 и 36 это — 12. После сокращения от 24 остается 2, от 36 — 3.

Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а при делении степеней показатели вычитаем.

a² и a⁷ сокращаем на a². При этом в числителе от a² остается единица (1 пишем только в том случае, когда кроме нее после сокращения других множителей не осталось. От 24 осталась 2, поэтому 1, оставшуюся от a², не пишем). От a⁷ после сокращения остается a⁵.

b и b сокращаем на b, полученные в результате единицы не пишем.

c³º и с⁵ сокращаем на с⁵. От c³º остается c²⁵, от с⁵ — единица (ее не пишем). Таким образом,

Числитель и знаменатель данной алгебраической дроби — многочлены. Сокращать члены многочленов нельзя! (нельзя сократить, к примеру, 8x² и 2x!). Чтобы сократить эту дробь, надо многочлены разложить на множители. В числителе есть общий множитель 4x. Выносим его за скобки:

И в числителе, и в знаменателе есть одинаковый множитель (2x-3). Сокращаем дробь на этот множитель. В числителе получили 4x, в знаменателе — 1. По 1 свойству алгебраических дробей, дробь равна 4x.

Сокращать можно только множители (сократить данную дробь на 25x² нельзя!). Поэтому многочлены, стоящие в числителе и знаменателе дроби, нужно разложить на множители.

В числителе — полный квадрат суммы, в знаменателе — разность квадратов. После разложения по формулам сокращенного умножения получаем:

Сокращаем дробь на (5x+1) (для этого в числителе зачеркнем двойку в показатель степени, от (5x+1)² при этом останется (5x+1)):

В числителе есть общий множитель 2, вынесем его за скобки. В знаменателе — формула разности кубов:

В результате разложения в числителе и знаменателе получили одинаковый множитель (9+3a+a²). Сокращаем дробь на него:

Многочлен в числителе состоит из 4 слагаемых. Группируем первое слагаемое со вторым, третье — с четвертым и выносим из первых скобок общий множитель x². Знаменатель раскладываем по формуле суммы кубов:

В числителе вынесем за скобки общий множитель (x+2):

Сокращаем дробь на (x+2):

Сокращать можем только множители! Чтобы сократить данную дробь, нужно стоящие в числителе и знаменателе многочлены разложить на множители. В числителе общий множитель a³, в знаменателе — a⁵. Вынесем их за скобки:

Множители — степени с одинаковым основанием a³ и a⁵ — сокращаем на a³. От a³ остается 1, мы ее не пишем, от a⁵ остается a². В числителе выражение в скобках можно разложить как разность квадратов:

Сокращаем дробь на общий делитель (1+a):

А как сокращать дроби вида

в которых стоящие в числителе и знаменателе выражения отличаются только знаками?

Примеры сокращения таких дробей мы рассмотрим в следующий раз.

2 комментария

Очень хороший сайт,каждый день им пользуюсь, и помогает. До того как я наткнулся на этот сайт,я не умел многое решать по алгебре, геометрии,но благодаря этому сайту мои оценки а 3 поднялись на 4-5. Теперь я могу смело сдавать ОГЭ,и нн боятся что его не сдам! Учитесь,и у Вас все получится!

Витя, желаю Вам успехов в учебе и высоких результатов на экзаменах!

А если в выражении стоит корень?

Его тоже можно сократить. Только опять же, соблюдая правила. Причем верны все те, которые были описаны выше. В общем, если стоит вопрос о том, как сократить дробь с корнями, то нужно делить.

На иррациональные выражения тоже можно разделить. То есть если в числителе и знаменателе стоят одинаковые множители, заключенные под знак корня, то их можно смело сокращать. Это приведет к упрощению выражения и выполнению задания.

Если после сокращения под чертой дроби осталась иррациональность, то от нее нужно избавиться. Другими словами, умножить на нее числитель и знаменатель. Если после этой операции появились общие множители, то их снова нужно будет сократить.

Вот, пожалуй, и все о том, как сокращать дроби. Правил немного, а запрет один. Никогда не сокращать слагаемые!

Без знания того, как сократить дробь, и наличия устойчивого навыка в решении подобных примеров очень непросто изучать в школе алгебру. Чем дальше, тем больше на базовые знания о сокращении обыкновенных дробей накладывается новой информации. Сначала появляются степени, потом множители, которые позже становятся многочленами.

Как тут не запутаться? Основательно закреплять умения в предыдущих темах и постепенно готовиться к знаниям о том, как сократить дробь, усложняющуюся год от года.