Как переводить десятичные дроби в обыкновенные

Округление результата преобразования простой дроби в десятичную

Следует заметить, что, в отличие от такого процесса, как преобразование десятичной дроби, эта процедура за частую может длиться бесконечно долго. В таких случаях говорят, что результат процедуры обращения обычной дроби в десятичную не может быть точным. Впрочем, практика показывает, что в подавляющем большинстве получение идеально точного результата и не требуется. Как правило, процесс деления заканчивается тогда, когда в его ходе уже получены значения тех десятичных долей, которые представляют в каждом конкретном случае практический интерес.

Пример 1

Требуется разрезать кусок масла весом один килограмм на девять одинаковых по своей массе частей. При выполнении этой процедуры оказывается, что масса каждой из них равняется / килограмма. Если по всем правилам осуществлять преобразование этой обычной дроби в дробь десятичную, то получится, что масса каждой из получившихся частей равняется ноль целых и один в периоде килограмма.

Определить массу совершенно точно не представляется возможным, поскольку деление можно осуществлять бесконечно. Для того чтобы его остановить, полученную величину просто округляют до какого-либо знака после запятой (как правило, до второго).

Округление ведется по стандартным правилам, предусмотренным в арифметике: если первая из «отбрасываемых» цифр имеет значение и более, то последняя из значимых увеличивается на единицу. В противном случае она остается неизменной.

Пример 2

Преобразовать обычную дробь одна восьмых в дробь десятичную.

Решение:

При делении единицы на восемь получается ноль целых сто двадцать пять тысячных или округлённо — ноль целых тринадцать сотых.

На практике преобразование десятичной дроби в простую и обратно подчиняется некоторым важным правилам целесообразности. К примеру, даже если тогда, когда простую можно обратить в десятичную абсолютно точно, но с большим количеством знаков после запятой, преобразование обычно заканчивают на некотором значимом для практических целей разряде.

Пример 3

Преобразовать обычную дробь девять тридцать вторых в дробь десятичную.

Решение:

Виды дробей

Дробь — это число, в состав которого входит одна доля или несколько её частей, поделенных на равные части. По сути, это отношение двух значений. Обыкновенное дробное выражение записывают с помощью натуральных чисел, разделённых горизонтальной чертой. Называется она винкулумом. В литературе можно встретить и другой тип записи с наклонной чертой (солидус).

Верхнее число, или стоящее слева от черты, называют числителем или делимым, а нижнее — знаменателем (делителем). Что такое дробь, удобнее всего объяснить на примере. Пусть на столе стоит тарелка, на которой лежит пирог. Он один и целый. Можно взять нож и разделить его на шесть равных частей.

По сути, количество пирога не изменится, поэтому, с математической точки зрения, на тарелке будет всё так же находиться целый пирог. Если с неё взять два куска, то целостность нарушится. Записывают это действие с помощью дроби: 2/6. То есть внизу указывают число, обозначающее, на сколько поделили пирог, а сверху — сколько кусков забрали.

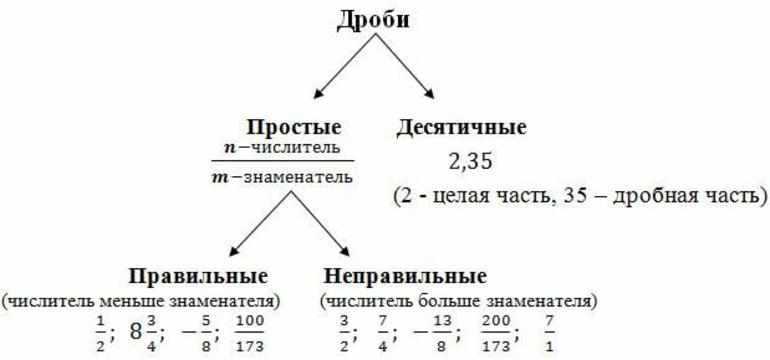
Дробь — это число, обозначающее часть целого предмета. При этом дробное отношение всегда будет меньше единицы. Существующие отношения принято разделять на следующие виды:

1. Правильные — отношения, в которых числитель меньше знаменателя.
2. Неправильные — дроби, где делимое по величине превышает делитель.
3. Смешанные — состоящие из суммы натурального и дробного числа.
4. Десятичные — в знаменателе которых стоит натуральное число с размерностью кратной десяти.
5. Составные — состоящие из нескольких черт дроби.

С дробными отношениями можно выполнять любые математические действия. Их складывают, вычитают, умножают, возводят в степень. Замечательным свойством дробей есть возможность их преобразования из одного вида в другой. Например, можно перевести обычную дробь в десятичную, неправильную — в смешанную. При этом операции возможны как в одну, так и другую сторону.

Проводимые операции, кроме получения периодической дроби, можно выполнять и в обратную сторону. Остаток при делении должен всегда быть меньше делителя. Поэтому, если при действии получается ноль, деление прекращается, а если остаток — бесконечная периодическое отношение.

Чаще всего для того, чтобы преобразовать простую дробь в десятичную, необходимо выполнить три шага:

1. Сократить выражение, требующее преобразования.
2. Разделить удобным способом числитель на знаменатель. В зависимости от величины значений, стоящих в числителе и знаменателе, это можно сделать столбиком или в уме. Если при делении остаток выходит отличным от нуля, то поставить запятую и продолжить искать частное.
3. Записать найденный результат с использованием запятой.

Нужно отметить, что алгоритм, объясняющий правило того, как перевести обыкновенную дробь в десятичную, подходит лишь для случаев, когда знаменатель раскладывается на множители пять и два. В иных случая получится периодическое десятичное число.

Перевод десятичных чисел в обыкновенную дробь

Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.

Представление дробей

Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:

• 0,5 = 1/2;
• 0,25 = 1/4;
• 1,375 = 11/8.

И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.

Избавляемся от запятой

Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:

Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.

Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:

• 0,5/1 = 5/10;
• 0,25/1 = 2,5/10 = 25/100;
• 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Шаг 3: Сокращаем полученные дроби до удобоваримого вида:

• 5/10 = 1 × 5 / 2 × 5 = 1/2;
• 25/100 = 1 × 25 / 4 × 25 = 1/4;
• 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.

Избавляемся от запятой еще проще

Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.

Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.

Шаг 2: Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:

• для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
• для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.

По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.

Шаг 3: Сокращаем нули и получаем итоговый результат:

• 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
• 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.

Преобразование на слух

Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.

0,025 = 25/1000 = 1/40

Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.

Примеры использования дробей в повседневной жизни

На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.

Работа

Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.

К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:

0,12 = 12/100 = 3/25

Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.

Преобразования «на слух»

Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.

А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.

Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:

\

Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому

\

А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому

\

В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 103, а 10 = 2 ∙ 5, поэтому

\

Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.

На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».

1. Сравнение дробей
2. Периодические десятичные дроби
3. Тригонометрические функции
4. Что такое числовая дробь
5. Задачи на проценты считаем проценты с помощью формулы
6. Более сложные задачи на производительность

Дробь с целым числом

Необходимо рассмотреть и другие примеры, с повышенной сложностью. Стоит взять 2,25. Как и до этого, для начала, лучше всего правильно обозначить название дроби. В этот раз имеется две целых, двадцать пять сотых. В связи с тем, что после знака находится две цифры, то они являются сотыми.

Как десятичную дробь перевести в обыкновенную дробь:

• Нецелая часть записывается в виде 25/100.
• Осталось дописать две целых. Они ставятся в начало, и таким образом получается смешанная дробь.
  
• 25/100 можно сократить. Для простоты, реально начинать с деления на 5, но неплохо сразу воспользоваться числом 25. В результате сокращения получается ¼.
• Остается лишь подписать две целые к ¼. Результат – 2 ¼.

Наконец, стоит рассмотреть и процесс работы с тысячными. Для разбора возьмем 4,112. Вновь работу нужно начать с верного прочтения. Получится четыре целых, сто двенадцать тысячных. Без труда удастся выделить первую цифру, 4, а затем подставить к ней сто двенадцать тысячных. Они выглядят так – 112/100.

Остается лишь сократить, чтобы придать лучший вид. В этом конкретном примере общим делителем является шесть. Результат – простая дробь 4 14/125.

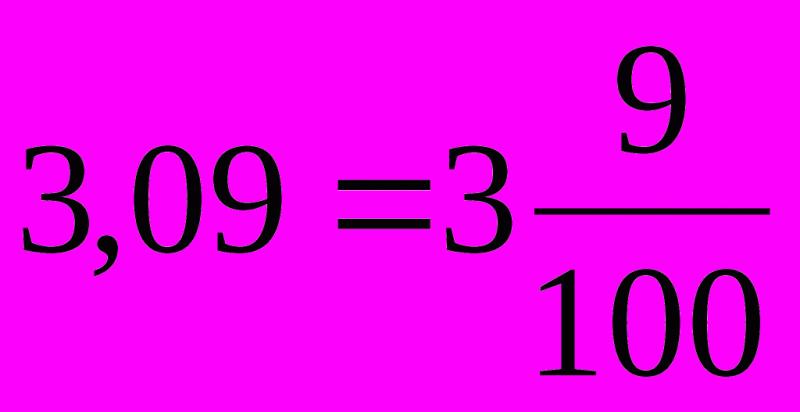
Что делать с целой частью

На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.

Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:

\

Затем вспоминаем про «утерянную» единицу и дописываем её спереди:

\

Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:

\

В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)

В заключение хотел бы рассмотреть ещё один приём, который многим помогает.

Что дальше?

Хотите узнать самые быстрые и простые способы конвертировать градусы Фаренгейта в градусы Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градусы Фаренгейта (или наоборот).

Вы изучаете логарифмы и натуральные логарифмы на уроках математики? У нас есть руководство по всем правила естественного журнала ты должен знать.

Знаете ли вы, что вода имеет особую плотность? Ознакомьтесь с нашим руководством, чтобы узнать какая плотность воды и как может измениться плотность.

Есть друзья, которым тоже нужна помощь в подготовке к экзаменам?

Перевести обычную дробь в десятичную возможно несколькими способами

После того, как стало понятно, какие дроби можно переводить из обычных в десятичные, можно приступить, собственно, к самому преобразованию. На самом деле, нет ничего сверхсложного, даже для того, у кого школьная программа окончательно «выветрилась» из памяти.

Как переводить дроби в десятичные: наиболее простой метод

Этот способ перевода обычной дроби в десятичную, действительно, является наиболее простым, однако многие люди даже не догадываются о его бренном существовании, так как в школе все эти «прописные истины» кажутся ненужными и не очень-то важными. Между тем, разобраться сможет не только взрослый, но легко воспримет подобную информацию и ребенок.

Итак, чтобы преобразовать дробь в десятичную, нужно умножить числитель, равно как и знаменатель, на одно число. Однако все не так просто, так в результате, именно в знаменателе должно получиться 10, 100, 1000, 10 000, 100 000 и так далее, до бесконечности. Не стоит забывать предварительно проверить, точно ли можно данную дробь превратить в десятичную.

Рассмотрим примеры:

Допустим, нам нужно провести преобразование дроби 6/20 в десятичную. Производим проверку:

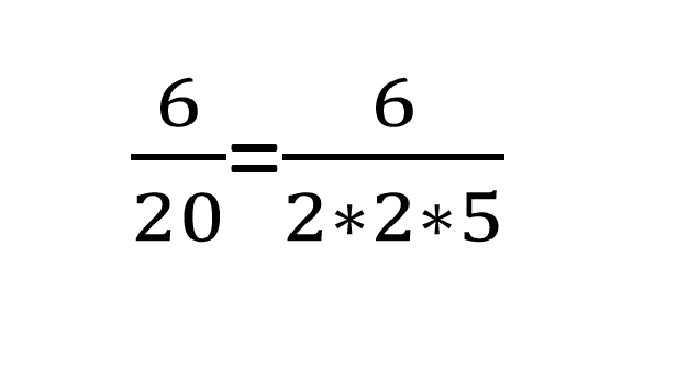
После того, как мы убедились, что перевести дробь в десятичную дробь, да еще и конечную, все же, возможно, так как ее знаменатель легко раскладывается на двоечки и пятерки, следует приступить к самому переводу. Самым лучшим вариантом, по логике вещей, чтобы умножить знаменатель и получить результат 100, является 5, так как 20х5=100.

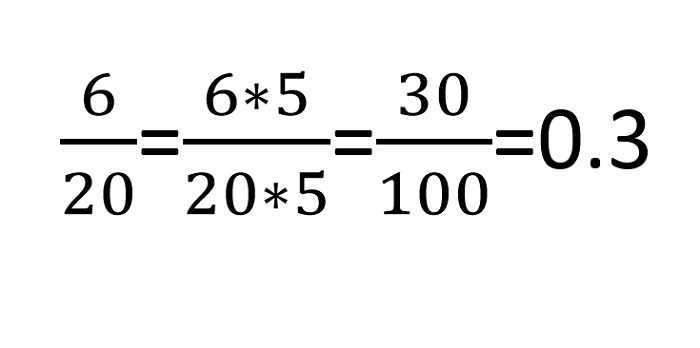
Можно рассмотреть дополнительный пример, для наглядности:

Второй и боле популярный способ переводить дроби в десятичные

Второй вариант несколько сложнее, однако он пользуется большей популярностью, ввиду того, что он гораздо проще для понимания. Тут все прозрачно и ясно, потому давайте сразу же перейдем к вычислениям.

Стоит запомнить

Для того, что правильно преобразовать простую, то есть обычную дробь в ее десятичный эквивалент, нужно числитель разделить на знаменатель. По сути, дробь – это и есть деление, с этим не поспоришь.

Рассмотрим действие на примере:

Итак, первым делом, чтобы перевести дробь 78/200 в десятичную, нужно ее числитель, то есть число 78, разделить на знаменатель 200. Но первым делом, что должно войти в привычку, нужно произвести проверку, о которой уже говорилось выше.

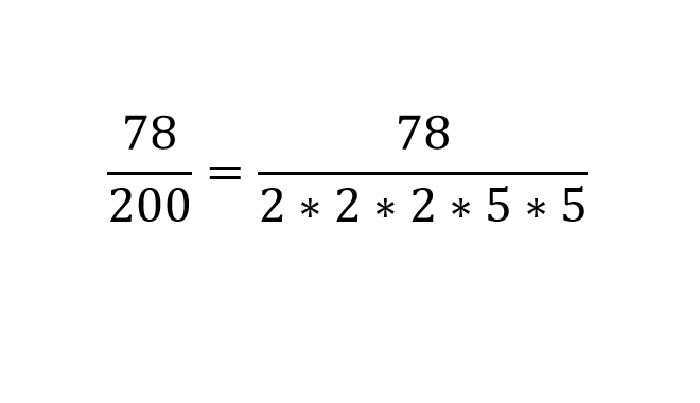
После произведения проверки, нужно вспомнить школу и делить числитель на знаменатель «уголком» или «столбиком».

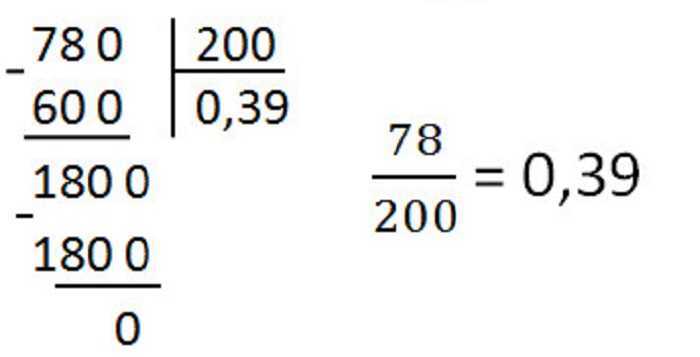
Как видите, все предельно просто, и семи пядей во лбу, чтобы легко решать подобные задачки вовсе быть не требуется. Для простоты и удобства приведем также и таблицу самых популярных дробей, которые просто запомнить, и даже не прилагать усилий, чтобы их переводить.

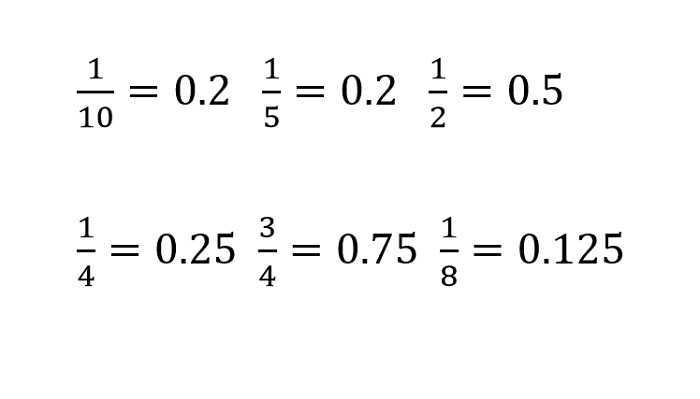
Десятичные дроби — коротко о главном

1. Определение

2. Конечная и бесконечная десятичная дробь

Десятичная дробь может быть:

• конечной, если она содержит конечное число цифр после запятой (\( \displaystyle \frac{8}{10},\ \frac{13}{100},\frac{49}{1000}\));
• бесконечной, в том числе периодичной, если конечное число цифр определить не определено (\( 0,05882352941…\));
• периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (\( \displaystyle \frac{1}{7}=0,\underbrace{142857}_{{период}}\underbrace{142857}_{период}142…=0,\left( 142857 \right)\))

3. Свойства десятичных дробей

• Десятичная дробь не меняется, если справа добавить нули \( \displaystyle \frac{3}{100}=0,03=0,030=0,030000\)и т.д.;
• Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: \( 0,014330000=0,01433\);
• Десятичная дробь возрастает в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: \( 0,0125\cdot 100=1,25\) (перенесли запятую на \( 2\) знака вправо – умножили на \( 100\) и дробь возросла в \( 100\) раз);
• Десятичная дробь уменьшается в \( 10\), \( 100\), \( 1000\) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: \( 124,56:100=1,2456\) (перенесли запятую на \( 2\) знака влево – разделили на \( 100\) и дробь уменьшилась в \( 100\) раз).

4. Сложение десятичных дробей

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.

5. Вычитание десятичных дробей

Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:

6. Умножение десятичных дробей

Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа

При умножении нам неважно, стоят ли запятые под запятыми и так далее

Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.

7. Деление десятичных дробей

Деление десятичной дроби на натуральное число

• Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
• Ставим в частном запятую, когда заканчивается деление целой части делимого.

Деление десятичных дробей друг на друга

Виды дробей. Преобразования.

Дроби бывают трёх видов.

1. Обыкновенные дроби

, например:

Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем
, нижнее — знаменателем.
Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз
апомни! Ззззз
наменатель — вниззззз
у!» Глядишь, всё и ззззапомнится.)

Более быстрый способ

Чтобы перейти от смешанной к фракции, умножьте целое число на знаменатель входящей в него дроби, к этому результату добавляется числитель и, следовательно, получается числитель новой дроби. Знаменатель совпадает с дробью, которая сопровождает целое. В этом видео мы объясняем, как преобразовать неправильную фракцию в смешанное число и наоборот. Помните, что операция перехода от смешанного числа к неправильной фракции уже была замечена в более раннем видео, которое мы рассмотрим здесь. Предположим, что у нас есть смешанное число, и нам предлагается преобразовать его в дроби.

Чёрточка, что горизонтальная, что наклонная, означает деление
верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.

Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.

32/8 = 32: 8 = 4

Быстрый метод говорит нам, что для преобразования просто поставить один и тот же знаменатель. Тогда числитель будет умножением целого числа на знаменатель плюс сумма начального числителя. Теперь давайте научимся передавать дробное число в смешанное число. Этот метод работает для неправильных дробей, которые являются числами, которые числитель больше знаменателя. Каждое число, когда мы его делим, может найти фактор без проблем, потому что знаменатель нерегулярности всегда больше. Первое, что мы собираемся найти, — это частное, которое мы ставим как целое число смешанного выражения.

Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.

2. Десятичные дроби

, например:

Именно в таком виде нужно будет записывать ответы на задания «В».

3. Смешанные числа

, например:

В качестве знаменателя фракции выражения поместим знаменатель начальной дроби, которую мы даем преобразовать. Тогда тогда знаменатель, который нам нужен, будет остатком и, следовательно, мы получим смешанную долю. Если мы хотим убедиться, что преобразование является хорошим, мы выполняем процедуру преобразования из дробного числа в смешанное число, которое мы изначально объяснили

Мы должны принять во внимание, что процесс преобразования из дробного в смешанное, который мы только что объяснили, требует, чтобы фракция была полностью упрощена

Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.

Наиболее универсальны обыкновенные дроби
. С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями
!

Чтобы сделать эти преобразования, мы будем использовать примеры. Если мы возьмем число 5, чтобы представить его как дробь, достаточно найти число, деленное на другое число, и результат будет равен. Если мы возьмем число 0, 2, мы должны помнить, что десятая часть — из десяти, а сотые — из стотысячной, из тысячи, поэтому, чтобы превратить 0, 2 в дроби, просто исключите запятую и получите номер 2, поэтому знаменатель будет Число, которое представляет десятичное место, затем.

Путь наименьшего сопротивления: удобные онлайн сервисы

1. 25, удаление запятой в числителе составляет 125, знаменатель равен 100, поскольку десятичные разряды находятся в сотых долях. Если мы разделим числитель каждой фракции выше на соответствующий знаменатель, мы придем к соответствующему ему десятичному значению.

Выражение величин в дробном виде

Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:

Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:

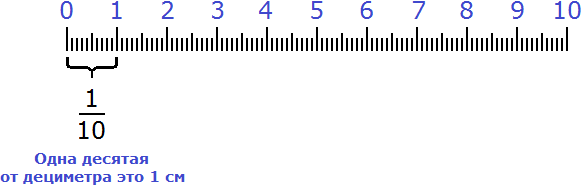
Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.

Итак, 6 целых сантиметров у нас уже есть:

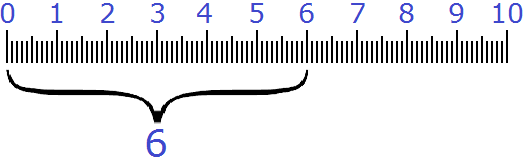
Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах?

На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см

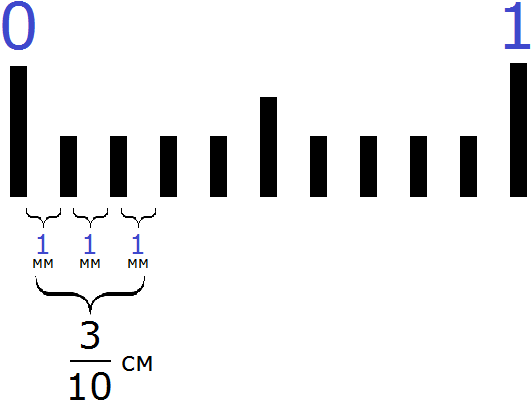
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.

В результате имеем шесть целых сантиметров и три десятых сантиметра:

Цифра 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».

Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.

Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6

6

Целая часть записана. Сразу же после написания целой части ставим запятую:

6,

И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:

6,3

Любое число, которое представляется в таком виде, называется десятичной дробью.

Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:

6,3 см

На рисунке выглядеть это будет так:

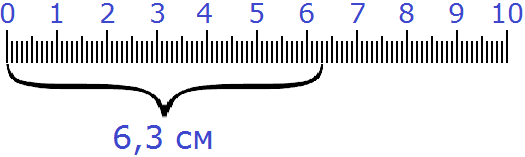
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1 000 или 10 000.

Как и смешанное число, десятичная дробь имеет цéлую часть и дробную.

Например, в смешанном числе целая часть это 6, а дробная часть это .

В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.

Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.

Так, дробь без знаменателя будет записана так:

0,5

Читается как «ноль целых, пять десятых».