Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры. перевод десятичных чисел в дробь и наоборот

Перевод обыкновенных дробей в десятичные дроби

Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби.

После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.

Теперь обо всем по порядку.

Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби

Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.

«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь

После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.

Рассмотрим применение этого правила при решении примеров.

Переведите правильную обыкновенную дробь 37/100 в десятичную.

Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера.

Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.

Разберем применение этого правила при решении примера.

Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.

Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.

Переведите смешанное число

Запишем все решение кратко:

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.

Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел, а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.

Переведите обыкновенную дробь 621/4 в десятичную дробь.

Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:

Для закрепления материала рассмотрим решение еще одного примера.

Переведите обыкновенную дробь 21/800 в десятичную дробь.

Запишите обыкновенную дробь 19/44 в виде десятичной дроби.

Для перевода обыкновенной дроби в десятичную выполним деление столбиком:

В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.

Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.

Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби

Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?

Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.

Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.

Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.

Умножение десятичных дробей: общие принципы

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Вычислите произведение 1 , 5 и 0 , 75 .

Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0 , 75 – это 75 / 100 , а 1 , 5 – это 15 10 . Мы можем сократить дробь и произвести выделение целой части. Полученный результат 125 1000 мы запишем как 1 , 125 .

Ответ: 1 , 125 .

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Умножьте одну периодическую дробь 0 , ( 3 ) на другую 2 , ( 36 ) .

Для начала приведем исходные дроби к обыкновенным. У нас получится:

0 , ( 3 ) = 0 , 3 + 0 , 03 + 0 , 003 + 0 , 003 + . . . = 0 , 3 1 — 0 , 1 = 0 , 3 9 = 3 9 = 1 3 2 , ( 36 ) = 2 + 0 , 36 + 0 , 0036 + . . . = 2 + 0 , 36 1 — 0 , 01 = 2 + 36 99 = 2 + 4 11 = 2 4 11 = 26 11

Следовательно, 0 , ( 3 ) · 2 , ( 36 ) = 1 3 · 26 11 = 26 33 .

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Ответ: 0 , ( 3 ) · 2 , ( 36 ) = 0 , ( 78 ) .

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Вычислите произведение 5 , 382 … и 0 , 2 .

Решение

У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5 , 382 … ≈ 5 , 38 . Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5 , 38 · 0 , 2 = 538 100 · 2 10 = 1 076 1000 = 1 , 076 .

Ответ: 5 , 382 … · 0 , 2 ≈ 1 , 076 .

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Можно ли любую обыкновенную дробь перевести в десятичную

Ответ на этот вопрос — «Да». Любую обыкновенную дробь можно записать в виде конечной или бесконечной десятичной, периодической дроби. У каждой дроби всегда есть эквивалентное представление в десятичной форме.

Теперь, прежде чем вы приступите к преобразованию обыкновенной дроби в десятичную, обратите внимание на следующие полезные советы:

1. Используйте калькулятор: Если у вас есть доступ к калькулятору, лучше воспользуйтесь им для выполнения деления. Это упростит и ускорит процесс.
2. Округление: При округлении десятичной дроби рекомендуется использовать «четное округление», то есть округлять до ближайшего четного числа.
3. Проверьте результат: После окончания преобразования проверьте результат с помощью других методов или калькулятора, чтобы убедиться в его точности.

Выводы:

Перевод обыкновенной дроби в десятичную форму может быть выполнен различными способами, включая деление числителя на знаменатель и умножение на определенное число

Независимо от выбранного подхода, важно следовать указанным шагам и быть внимательным при округлении результатов. При необходимости всегда лучше проверять результаты с помощью других методов или с использованием калькулятора, чтобы быть уверенным в их точности

Можно ли бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби

Для доказательства этого факта необходимо воспользоваться алгебраическими операциями и свойствами рациональных чисел. Первым шагом можно представить бесконечную десятичную периодическую дробь в виде обыкновенной бесконечной десятичной периодической дроби, умножив исходную дробь на 10. Затем, в результате вычислений, можно выделить две части этой периодической дроби — целую и периодическую.

Затем, используя формулы и свойства обыкновенных дробей, можно свести данную бесконечную периодическую дробь к виду обыкновенной. Если период равен нулю, то получится обыкновенная дробь без остатка, а если период не равен нулю, то бесконечную периодическую дробь можно записать в виде обыкновенной, где числитель выражен через разность между периодом и целой частью, а знаменатель равен разности между числителем и целой частью.

Таким образом, любую бесконечную десятичную периодическую дробь можно записать в виде обыкновенной дроби, что означает, что она является рациональным числом.

Как десятичную дробь прибавить к обычной дроби

Для сложения десятичных дробей необходимо следовать нескольким шагам. В начале, нужно записать оба числа одно под другим так, чтобы запятая стояла под запятой в обоих числах. Затем производится сложение чисел, при этом сложение осуществляется как обычное сложение чисел в столбик, начиная с самого правого разряда. После сложения всех разрядов, запятая в итоговом ответе будет расположена под запятой. Если в процессе сложения получилось число, у которого количество разрядов после запятой больше, чем десятичная дробь, пишется результат с штрихом на запятой и продолжается сложение следующих разрядов. Итоговая сумма будет содержать десятичную дробь, если она присутствовала в исходных числах.

Как преобразовать десятичную дробь в обыкновенную примеры

Далее мы должны упростить полученную обыкновенную дробь. Для этого умножим числитель и знаменатель на 10, пока в числителе не станет только цифры после запятой. Например, в случае с дробью 0,35 мы умножаем числитель и знаменатель на 10, получаем 3,5/10. При этом, если в какой-то момент мы получаем дробь без нулей после запятой, мы умножаем числитель и знаменатель на 1000, 10000 и так далее, чтобы убрать все цифры после запятой в числителе.

После упрощения дроби, мы можем сократить ее, если это возможно. Для этого находим наибольший общий делитель числителя и знаменателя и делим оба на него. В итоге получается обыкновенная дробь в виде a/b, где a и b — целые числа.

Как разделить обыкновенную дробь на целое число

Для того чтобы разделить обыкновенную дробь на целое число, нужно умножить знаменатель дроби на данное целое число, а числитель оставить без изменений. Например, если у нас есть дробь 3/4 и мы хотим разделить ее на число 2, мы умножаем знаменатель 4 на 2 и получаем 8. Числитель остается без изменений и равен 3. Таким образом, исходная дробь 3/4 разделяется на 2, и мы получаем дробь 3/8. Это означает, что одна часть дроби 3/4 равна 3/8. Таким образом, мы можем разделить обыкновенную дробь на целое число, умножив знаменатель на это число и оставив числитель без изменений.

Условие умножения десятичной дроби с натуральным показателем

Принцип умножения дробей данного вида, такой же как и между десятичными. Используются и принимаются к сведению все те правила, которые были изучены ранее.

Подробно рассмотрим на примерах и решим их.

Пример №1:

Нам нужно вычислить произведение из числовых значений.

\

Для этого воспользуемся правилом умножения через столбик.

Следовательно, ответ задачи, исходя из вычисления равен: 34,05.

Пример №2:

Даны числовые значения 0,(42) и 22. Необходимо найти их произведение.

Для начала преобразуем периодическую дробь в обычную.

И получим следующее выражение:

\

Следом проводим умножение: \.

Итоговый результат, будет записываться в виде периодической дроби, как и было задано изначально.

Ответ: \

Пример №3:

Даны значения и нужно их умножить \

Для начала округляем бесконечную дробь до сотых значений. Умножаем полученные значения и получаем окончательный ответ к задаче.

\

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Дистанционные курсы для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Только 23 февраля!Получите новую специальность по низкой цене

Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

Зачем уметь работать с дробями?

Дроби используются в различных областях жизни, в том числе:

• Математика: вычисление дробных величин, операции с дробями и т.д.
• Кулинария: расчет ингредиентов для приготовления блюд.
• Финансы: вычисление процентов, деление денежных сумм на части и т.д.
• Строительство: расчет объема материалов и работ.
• Производственные процессы: расчет долей ресурсов и материалов.
• Образование: вычисление средних оценок, расчет долей в статистике.
• Медицина: расчет доз лекарств и необходимого количества компонентов.
• Геодезия: расчет длины линий и площади.
• Дизайн: расчет пропорций и размеров.
• Технологии: расчет долей энергии, памяти, дискового пространства и т.д.

И это далеко не полный список – дроби можно встретить и во многих других сферах. И в каждой из этих областей дроби используются для точного вычисления величин и удобного представления частей целого.

Кроме того, решение математических задач – прекрасный инструмент для тренировки математических навыков и отличная гимнастика для мозга. Вот лишь несколько причин, почему полезно время от времени умножать дроби и решать другие примеры:

• Это развивает логику: математические задачи требуют применения логических умений, учат связывать факты и делать выводы.
• Это улучшает память: математика требует запоминать формулы и методы решения задач, что способствует улучшению памяти.
• Это способствует креативному мышлению: некоторые математические задачи требуют применения нестандартных подходов и инициативности.
• Это улучшает мышление: математическая активность тренирует мозг на устойчивость к сложным концептам и улучшает способность к анализу и синтезу.

В целом, решение математических задач может улучшать ментальные способности и способствовать развитию мозга. Поэтому знать, как умножать дроби, и уметь это делать полезно любому человеку, а школьникам, студентам и специалистам, чья деятельность связана с математикой, особенно.

Как умножать дроби?

Здесь необходимо разобрать три основных случая: когда требуется умножить дробь на дробь, когда требуется перемножить смешанные дроби и когда требуется умножить дробь на натуральное число.

Умножение дроби на дробь

Умножить дробь на дробь очень просто. Для этого нужно числитель одной дроби умножить на числитель другой, и точно так же поступить со знаменателями. В процессе также стоит подумать, можно ли дробь сократить.

Пример:

Говоря проще, числитель будет равен произведению числителей обеих дробей, а знаменатель будет равен произведению знаменателей

Это правило применимо ко всем дробям как с одинаковыми, так и с разными знаменателями. Когда дробь большая (к примеру, 26/₃₇), можно попробовать сократить ее сразу, чтобы производить вычисления было проще.

В случае, когда в примере есть смешанное число, сначала нужно преобразовать его в неправильную дробь, а затем умножить предлагаемым способом, а итоговый результат вновь преобразовать в смешанное число.

Умножение десятичных дробей

Чтобы умножить десятичные дроби, нужно следовать алгоритму:

• Записать дроби столбиком и умножить, как на натуральные числа (запятые пока в расчет не берем).
• Посмотреть, сколько знаков после запятой имелось в дробях, и сложить их количество.
• Справа налево отсчитать после умножения столько цифр, сколько знаков после запятой получилось на предыдущем этапе.
• Поставить запятую перед нужным количеством цифр.

Пример:

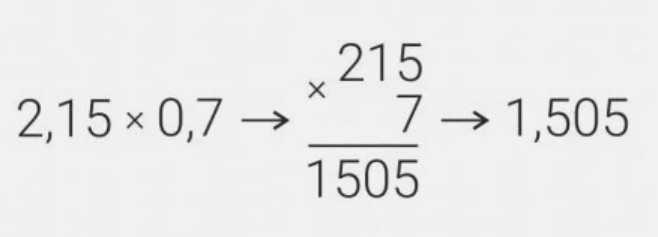
При умножении на 0,1, на 0,01, на 0, 001 и т.п. нужно переставить запятую влево на количество знаков, имеющееся после запятой в множителе. Например: 0,15 х 0,1 = 0,015 или 0,3 х 0,001 = 0,0003.

Топ вопросов за вчера в категории Математика

Математика 21.06.2023 06:59 938 Тупиков Сергей.

Запишите в десятичной записи число: а) 74; б) 350; в)636300; г)2800005.

Ответов: 1

Математика 15.06.2023 02:27 527 Журавель Настя.

Велосипед ехал 2,6 ч со скоростью 6,6 м/с,а затем 1,4 ч со скоростью 5,2 м/с.чему равна средняя скор

Ответов: 2

Математика 04.06.2023 14:00 557 Матвеева Лиля.

Запишите в десятичной записи число: а) 74, б) 350, в) 636 300 г) два миллиона восемьсот тысяч 5 д) 2

Ответов: 1

Математика 18.05.2023 04:51 869 Максимова Катя.

Найдите отношение длины диагонали листа формата а7 к его меньшей стороне ответ округлите до десятых

Ответов: 2

Математика 20.06.2023 17:50 190 Аветисян Карен.

Равны ли множества А и В А={1}, В=`1`

Ответов: 1

Математика 14.06.2023 02:36 237 Чиняев Глеб.

На одну порцию десерта из клубники берут 120г ягод и 25г сливок.Сколько сливок потребуется для приго

Ответов: 1

Математика 14.06.2023 11:22 397 Анфалова Татьяна.

Экскурсионный теплоход двигался 4,3 ч по озеру со скоростью 20км/ч, затем 2,5 ч по реке со скоростью

Ответов: 1

Математика 15.06.2023 03:21 285 Кулакова Лиза.

Найдите среднюю длину своего шага,измерив длину пяти своих шагов​

Ответов: 1

Математика 21.06.2023 08:32 177 Верхозин Александр.

2. Сколько лошадей в двух табунах, если в одном табуне 836 лошадей, а в другом на 308 больше? 3.Вычи

Ответов: 2

Математика 18.07.2023 20:29 90 Филимонов Захар.

10A ДОМАШНЕЕ ЗАДАНИЕ Узнай из диаграммы количество мест в построенных школах по годам. Запиши эти

Ответов: 1

Основные правила дробей

Прежде чем осваивать методы умножения дробей, необходимо усвоить несколько правил, которые могут пригодиться в самых разных ситуациях и заметно облегчить процесс решения задач. Эти правила таковы:

• Перед сложением или вычитанием дробей необходимо привести их к общему знаменателю.
• Умножение дробей производится путем умножения числителей и знаменателей.
• Деление дробей производится путем перемножения первой дроби на обратную второй дроби.
• После выполнения операций над дробями их можно сократить, деля числитель и знаменатель на их наибольший общий делитель (НОД). НОД нескольких чисел – это наибольшее натуральное число, на которое эти числа делятся без остатка.

В дополнение к этому:

• Если делитель дроби равен нулю, у дроби не будет значения.
• Дробь всегда будет равна нулю, если ее числитель равен нулю, а знаменатель не равен.
• Две дроби a/_bи c/_dбудут равными, если ad = bc.
• При умножении или делении числителя и знаменателя на одно и то же натуральное число значение дроби останется прежним.

Это основные правила работы с дробями, которые следует знать и применять при решении математических задач с использованием дробей.

Виды дробей. Преобразования.

Дроби бывают трёх видов.

1. Обыкновенные дроби

, например:

Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем
, нижнее — знаменателем.
Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз
апомни! Ззззз
наменатель — вниззззз
у!» Глядишь, всё и ззззапомнится.)

Более быстрый способ

Чтобы перейти от смешанной к фракции, умножьте целое число на знаменатель входящей в него дроби, к этому результату добавляется числитель и, следовательно, получается числитель новой дроби. Знаменатель совпадает с дробью, которая сопровождает целое. В этом видео мы объясняем, как преобразовать неправильную фракцию в смешанное число и наоборот. Помните, что операция перехода от смешанного числа к неправильной фракции уже была замечена в более раннем видео, которое мы рассмотрим здесь. Предположим, что у нас есть смешанное число, и нам предлагается преобразовать его в дроби.

Чёрточка, что горизонтальная, что наклонная, означает деление
верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.

Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.

32/8 = 32: 8 = 4

Быстрый метод говорит нам, что для преобразования просто поставить один и тот же знаменатель. Тогда числитель будет умножением целого числа на знаменатель плюс сумма начального числителя. Теперь давайте научимся передавать дробное число в смешанное число. Этот метод работает для неправильных дробей, которые являются числами, которые числитель больше знаменателя. Каждое число, когда мы его делим, может найти фактор без проблем, потому что знаменатель нерегулярности всегда больше. Первое, что мы собираемся найти, — это частное, которое мы ставим как целое число смешанного выражения.

Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.

2. Десятичные дроби

, например:

Именно в таком виде нужно будет записывать ответы на задания «В».

3. Смешанные числа

, например:

В качестве знаменателя фракции выражения поместим знаменатель начальной дроби, которую мы даем преобразовать. Тогда тогда знаменатель, который нам нужен, будет остатком и, следовательно, мы получим смешанную долю. Если мы хотим убедиться, что преобразование является хорошим, мы выполняем процедуру преобразования из дробного числа в смешанное число, которое мы изначально объяснили

Мы должны принять во внимание, что процесс преобразования из дробного в смешанное, который мы только что объяснили, требует, чтобы фракция была полностью упрощена

Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.

Наиболее универсальны обыкновенные дроби
. С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями
!

Чтобы сделать эти преобразования, мы будем использовать примеры. Если мы возьмем число 5, чтобы представить его как дробь, достаточно найти число, деленное на другое число, и результат будет равен. Если мы возьмем число 0, 2, мы должны помнить, что десятая часть — из десяти, а сотые — из стотысячной, из тысячи, поэтому, чтобы превратить 0, 2 в дроби, просто исключите запятую и получите номер 2, поэтому знаменатель будет Число, которое представляет десятичное место, затем.

Путь наименьшего сопротивления: удобные онлайн сервисы

1. 25, удаление запятой в числителе составляет 125, знаменатель равен 100, поскольку десятичные разряды находятся в сотых долях. Если мы разделим числитель каждой фракции выше на соответствующий знаменатель, мы придем к соответствующему ему десятичному значению.

Как перемножить десятичную дробь с обыкновенной или со смешанным числом

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Умножьте 0 , 4 на 3 5 6

Решение

​Cначала переведем десятичную дробь в обыкновенную. Имеем: 0 , 4 = 4 10 = 2 5 .

Далее считаем: 0 , 4 · 3 5 6 = 2 5 · 23 6 = 23 15 = 1 8 15 .

Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1 , 5 ( 3 ) .

Ответ: 1 , 5 ( 3 ) .

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Вычислите произведение 3 , 5678 . . . · 2 3

Решение

Второй множитель мы можем представить как 2 3 = 0 , 6666 …. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3 , 568 и 0 , 667 . Посчитаем столбиком и получим ответ:

Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2 , 379856 ≈ 2 , 380 .

Ответ: 3 , 5678 . . . · 2 3 ≈ 2 , 380

Источник

Сложные задачи

Задачи, в отличие от примеров, более приближены к реальным вычислениям. Они моделируют расчёты, которые могут быть востребованы по-настоящему в быту или при выполнении работы. При этом решать их гораздо интереснее, но и требуют они уже среднего или высокого уровня подготовки. Например:

1. Поставщик на рынок доставил пятнадцать ящиков бананов и двадцать пакетов с яблоками. Каждая упаковка весит 15, 5 килограммов. Рассчитать, сколько всего килограммов фруктов завезли на базу. В первом действии нужно узнать, сколько же всего было упаковок товара: 15 + 20 = 35 штук. Так как вес тары одинаков, то можно найти требуемый ответ простым умножением: 15, 5 * 35 = 542, 5 килограмма.
2. Грузовая машина на сто километров пройденного пути расходует 12 литров топлива. Молоковоз же расходует больше на 45 литра, а легковой автомобиль с прицепом больше молоковоза в 1, 5 раза. Определить, сколько топлива сжигает легковушка, проехавшая один километр пути. Ответ округлить до десятых. Вначале нужно найти, сколько же расходует горючего молоковоз на сто километров: 12 + 4, 5 = 16, 5 литров. Из условия следует, что легковушка потребляет бензина больше в полтора раза, поэтому её расход будет равен: 16, 5 * 1, 1 = 18, 5. В задаче спрашивается расход на один километр отсюда 18, 5 / 100 = 0, 1815 ≈ 0, 2 литра.
3. Дорога у школьницы до дома занимает 2 км. Утром она часто опаздывает в школу, поэтому ей приходится бежать. В этом случае время, которое ей нужно затратить на дорогу до школы, составляет 0, 35 часа. Обратно из школы девочка не торопится и идёт домой в течение 0, 5 часа. С какой скоростью ученица бежит в школу утром и с какой возвращается после уроков? Из курса физики известно, что скорость — это расстояние, делённое на время. Отсюда утренняя скорость школьницы равна: 2:0, 35 = 200 / 35 = 5, 7 км/ч. Аналогично можно найти скорость, с какой девочка возвращается: 2:0, 5 = (2/1) / (5/10) = (2 / 1) / (1 / 5) = (2 / 1) * (5 / 1) = 10 км/ч. Задача решена.