Свойства деления натуральных чисел, свойство деления суммы на число

Умножение натуральных чисел

Результат умножения натуральных чисел называют их произведением. Произведение двух натуральных чисел $a$ и $b$ содержит стольких единиц, сколько их содержится в числе $a$, взятых столько раз, сколько единиц содержится в числе $b$.

Рисунок 1.

Если произведение обозначить $c$, то говорят, что оно получено в результате умножения чисел $a$ и $b$. Записывается умножение двух чисел следующим образом:

$a\cdot b=c$ или $a\times b=c$.

Числа $n$ и $m$ называют множителями или сомножителями.

Рисунок 2.

Например, найдем произведение чисел $13\cdot 5$.

По определению операции умножения:

Умножение натуральных чисел

Если сумма со­сто­ит из рав­ных сла­га­е­мых, то ее можно за­пи­сать ко­ро­че: 25 + 25 можно за­пи­сать, как 25 * 2.  

.

На­ту­раль­ное число m умно­жить на на­ту­раль­ное число n – это зна­чит найти зна­че­ние суммы, ко­то­рая со­сто­ит из nсла­га­е­мых, каж­дое из ко­то­рых равно m. m яв­ля­ет­ся пер­вым мно­жи­те­лем, n яв­ля­ет­ся вто­рым мно­жи­те­лем, m * nяв­ля­ет­ся про­из­ве­де­ни­ем (рис. 1).

Рис. 1. Умно­же­ние

При­ме­ры: 1.

Про­из­ве­де­ние чисел 8 и x

8 * x.

2. Про­из­ве­де­ние суммы чисел a и b и числа 15

(а + в) * 15.

3. Про­из­ве­де­ние (m + 2) и (k — 3) (m + 2) * (k — 3).

Пер­вый мно­жи­тель – (m + 2), вто­рой мно­жи­тель – (k — 3)

4. Про­из­ве­де­ние 4ab со­сто­ит из трех мно­жи­те­лей: пер­вый мно­жи­тель – 4, вто­рой мно­жи­тель – a, тре­тий мно­жи­тель – в.

5. Число 12 можно пред­ста­вить в виде про­из­ве­де­ния несколь­ки­ми спо­со­ба­ми:

12 * 1

6 * 2

4 * 3

.

Свойство деления суммы двух натуральных чисел на натуральное число.

Чтобы свойство деления суммы двух натуральных чисел на данное натуральное число стало совсем очевидно, достаточно рассмотреть следующую ситуацию.

Между детьми в группе решили поровну разделить фрукты, которые находятся в двух пакетах (будем считать, что натуральные числа, определяющее количества фруктов в пакетах, можно разделить на натуральное число, соответствующее количеству детей в группе). Для этого можно сначала сложить вместе фрукты из двух пакетов, после чего разделить и раздать их. А можно сначала разделить фрукты из первого пакета и раздать их детям, после чего разделить фрукты из второго пакета и раздать их. Понятно, что и в том и в другом случае у каждого ребенка окажется одно и то же количество фруктов.

Теперь мы можем привести формулировку рассматриваемого свойства: разделить сумму двух натуральных чисел на данное натуральное число – это все равно, что сложить частные от деления каждого слагаемого на данное натуральное число.

Запишем это свойство деления с помощью букв. Пусть a, b и c – такие натуральные числа, что a можно разделить на c и b можно разделить на c, тогда (a+b):c=a:c+b:c. В правой части записанного равенства в первую очередь выполняется деление, после чего – сложение (при необходимости просмотрите материал статьи порядок выполнения действий).

Приведем пример, подтверждающий справедливость свойства деления суммы двух натуральных чисел на данное натуральное число. Покажем, что равенство (18+36):6=18:6+36:6 верное. Сначала вычислим значение выражения из левой части равенства. Так как 18+36=54, то (18+36):6=54:6. Из таблицы умножения находим 54:6=9 (смотрите раздел теории ). Переходим к вычислению значения выражения 18:6+36:6. Из таблицы умножения имеем 18:6=3 и 36:6=6, поэтому 18:6+36:6=3+6=9. Следовательно, равенство (18+36):6=18:6+36:6 верное.

Еще следует обратить внимание на тот факт, что это свойство, а также позволяют выполнять деление суммы трех и большего количества натуральных чисел на данное натуральное число. Например, частное (14+8+4+2):2 равно сумме частных следующего вида 14:2+8:2+4:2+2:2.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Правила деления по математике

Предоставление учащимся инструментов для решения деления с помощью этих сокращений не только делает деление менее сложным, но и превращает его в забавную головоломку. Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность расчета.

Каковы правила разделения?

Приступая к разделу о делении, обязательно поделитесь этими правилами с классом и обсудите их во время выступления по математике:

ДЕЛИМОСТЬ НА 2

Число, которое делится на 2, называется четным. Когда последняя цифра в числе равна 0 или даже четной, то есть 2, 4, 6 или 8, то число делится на 2. Например, 20 оканчивается на 0, поэтому оно делится на 2. Число 936 заканчивается в 6, а 6 четно. Значит, 936 делится на 2,9.0003

ДЕЛИМОСТЬ НА 3

Число делится на 3, если сумма цифр делится на 3. Чтобы использовать этот прием, учащиеся должны уметь делить, но проверка меньших чисел менее сложна, чем проверка больших. . Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:

1 + 6 + 8 = 15

15/3 = 5

Следовательно, 168 делится на 3.

ДЕЛИМОСТЬ НА 4

Если последние две цифры числа делятся на 4, то делится и все число. Например, в 1012 12 делится на 4.

ДЕЛИМОСТЬ НА 5

Когда последняя цифра числа 0 или 5, число можно разделить на 5 без остатка. Таким образом, 5, 10, 15, 20, 25 и т. д. можно разделить на 5. Учащиеся могут посмотреть на большие числа и сразу сказать, можно ли их поровну разделить на пять частей.

ДЕЛИМОСТЬ НА 6

Числа, которые делятся на 6, также можно разделить на как на 3, так и на 2. Учащиеся должны проверить число с обоими правилами для 3 и 2. Если число проходит оба теста, его можно разделить на 6. Если он провалит хотя бы один тест, он не сможет. Например:

308 оканчивается на четную цифру, поэтому оно делится на 2. Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.

ДЕЛИМОСТЬ НА 8

Большое число делится на 8, если последние три цифры также делятся на 8 или равны 000. В числе 7120 120 можно разделить на 8 без остатка, поэтому 7120 также делится на 8.

ДЕЛИМОСТЬ НА 9

Правило делимости 9 такое же, как и 3. Если сумма цифр числа делится на 9, так же как и весь номер. Например:

В числе 549 5 + 4 + 9 = 18

18/9 = 2

Итак, 549 делится на 9.

ДЕЛИМОСТЬ НА 10

Если последняя цифра 0, то число разделить на 10 поровну.

Почему правила помогают и как их использовать

Эти правила позволяют учащимся рассматривать большие числа в менее сложном контексте. Правила делимости также позволяют им многое узнать о числе, просто взглянув на его цифры. Таким образом, вы должны поощрять учащихся использовать все правила при изучении числа. Глядя на что-то вроде 1159,350, учащиеся могут пройтись по списку делимости, отметив, на какие числа можно разделить большее число.

Конечно, на уроках математики вы будете говорить не только о четных делениях. Некоторые числа будут иметь остатки. Вы все еще можете использовать правила, чтобы говорить об этих числах.

Связанные данные

• Фасонный стержень

  07 ноября 2022 г.

• Рене Беринг Директор по исследованиям в области образования, основная грамотность и раннее обучение

  Д-р Витас Лайтусис Директор по исследованиям в области образования, дополнительная математика и интервенция

  05 ноября 2022 г.
  

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим например 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

24 = 24

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

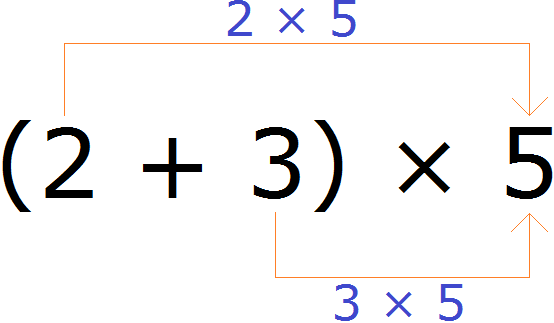
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25.

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

0 × 2 = 0

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Никак!

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

0 × 2 = 2 × 0

0 = 0

Примеры применения закона умножения на ноль:

5 × 0 = 0

5 × 5 × 5 × 0 = 0

2 × 5  × 0 × 9  × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

Страницы

• Главная страница
• 1. Натуральные числа
• 2. Точка. Прямая. Плоскость
• 3,4 Запись натуральных чисел. Классы в записи числа
• 5. Отрезок
• 6. Сравнение натуральных чисел
• 7. Луч
• 8, 9. Координатный луч
• 10, 11 Округление натуральных чисел
• 12, 13 Сложение натуральных чисел
• 14, 15, 16. Угол
• 17. Вычитание натуральных чисел
• 18. Ломаная
• 19, 20. Задачи на нахождение чисел по их сумме и разности
• 21, 22. Множества
• 23, 24, 25. Уравнения
• 26, 28. Обобщение по теме «Сложение и вычитание натуральных чисел»
• 29, 30, 31. Умножение натуральных чисел
• 32, 33. Степень числа с натуральным показателем
• 34, 35. Прямоугольник. Квадрат
• 36, 37, 38. Распределительный закон умножения
• 40. Деление натуральных чисел
• 41, 42. Задачи на нахождение двух чисел по их сумме и частному
• 43, 44. Задачи на нахождение чисел по их разности и частному
• 45, 46. Числовые выражения
• 47, 48, 49. Выражения с переменными
• 50, 51. Задачи на части
• 52. Обобщение по теме «Умножение и деление натуральных чисел»
• 56, 57. Делители и кратные
• 58. Признаки делимости на 2 и 4
• 59. Признаки делимости на 5 и 10
• 60, 61. Задачи на нахождение общих элементов множеств
• 62, 63. Деление с остатком
• 64, 65. Признаки делимости на 3 и на 9
• 66, 67. Прямоугольный параллелепипед. Куб
• 68, 69. Объем параллелепипеда
• 70, 71, 72. Задачи на движение
• 73, 74, 75. Задачи на движение по воде
• 76. Простые и составные числа
• 77, 78. Разложение числа на простые множители
• 79. Шкалы
• 80, 81. Измерение углов
• 82, 83. Общие делители. Взаимно простые числа
• 84, 85. Наибольший общий делитель
• 86, 87. Наименьшее общее кратное
• 88. Перпендикулярные и параллельные прямые
• 89, 90. Формулы
• 93, 94, 95. Задачи на нахождение элементов множест…
• 96, 97. Понятие дроби
• 98, 99. Дробь как частное от деления натуральных чисел
• 100. Какую часть одно число составляет от другого
• 101, 102. Нахождение части (дроби) от числа
• 103, 104. Нахождение числа по его части (дроби)
• 105, 106. Основное свойство дроби
• 107, 108. Сокращение дроби
• 109, 110. Приведение дробей к общему знаменателю
• 111, 112. Сравнение дробей
• Задания по теме «Дроби»
• 113, 114. Правильные и неправильные дроби
• 115, 116, Сложение дробей с одинаковыми знаменателями
• 117-120. Сложение дробей с разными знаменателями
• 121, 122. Законы сложения дробей
• 123, 124. Вычитание дробей с одинаковыми знаменателями
• 125, 126, 127. Вычитание дробей с разными знаменателями
• 131, 132. Умножение дробей
• 133, 134. Законы умножения дробей
• 139, 140. Деление дробей
• 141, 142, 143. Часть (дробь) от числа
• 144, 145. Задачи на совместную работу
• 146, 147, 148. Обобщение по теме «Умножение и деление дробей»
• 149, 150. Смешанные дроби
• 151, 152. Сравнение смешанных дробей
• 153, 154. Изображение дробей на координатном луче
• 155, 156. Сложение смешанных дробей
• 157, 158. Вычитание смешанных дробей
• 159, 160. Умножение и деление смешанных дробей
• 161, 162. Среднее арифметическое
• 163, 164, 165. Упражнения на все действия со смешанными дробями
• 166, 168. Обобщение «Смешанные дроби»
• 169, 170, 171. Повторение

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

1. Определяем сотни частного:

   Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

   Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.

2. Определяем десятки частного:

   Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

   Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.

3. Определяем единицы частного:

   47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

словесно:

1. Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.

2. К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.

3. Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

словесно:

1. Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.

2. Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.

3. Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.

4. Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.

Из предложенных примеров выводим следующее правило:

1. Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.

2. К остатку сносят следующую цифру делимого и снова задаются.

3. Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.

4. Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.

5. Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя

Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр

Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

словесно:

1. 8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.

2. Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.

3. Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Математика 5-6 классы. 3. Умножение и деление натуральных чисел

Подробности

Категория: Математика 5-6 классы

 Умножение, Законы умножения

Умножить натуральное число 3 на натуральное число 4—это означает найти сумму трех слагаемых, каждое из которых есть 4. Таким образом,3 • 4 = 4 + 4 + 4.Числа 3 и 4 называются множителями, а число 3 • 4 — их произведением.Для любого числа а верно равенство 1 • а=а.Вот еще примеры;5 • 3 — 3 + 3 + 3 + 3 + 3 = 15,3 • 1 = 1 + 1 + 1 =3,1 • 7 = 7.Для любых натуральных чисел а и b верно равенство а • b=b • а,выражающее переместительный или коммутативный закон умножения:От перестановки множителей произведение не изменяется.Переместительный закон умножения легко проверяется при подсчете двумя способами числа квадратов на рис. 1.2.

Все квадраты можно расположить в 3 ряда по 4 квадрата—всего 3 • 4 квадрата (рис. 1.3). Но можно расположить все квадраты в 4 столбца по 3 квадрата—всего 4 • 3 квадрата. Так как число квадратов в обоих случаях одно и то же, то3 • 4 = 4 • 3.Для любых натуральных чисел а, b и с верно равенство

(a • b) • c=a • (b • c),

выражающее сочетательный или ассоциативный закон умножения:Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение  второго и третьего чисел.Сочетательный закон легко проверяется при подсчете числа кубиков на рис. 1.4. Все кубики можно расположить в два слоя—нижний и верхний—по 3 • 4 кубика в каждом—всего 2 • (3 • 4) кубика (рис. 1.5).

Но можно расположить все кубики в 4 слоя по 2 • 3 кубика в каждом—всего 4 • (2 • 3) = (2 • 3) • 4 кубика.Так как число кубиков в обоих случаях одно и то же, то (2 • 3) • 4 = 2 • (3 • 4).Этим примером мы проиллюстрировали сочетательный закон умножения для натуральных чисел.Отметим, что произведение трех (и более) чисел можно записать и без скобок:(2 • 3) • 4 = 2 • (3 • 4) = 2 • 3 • 4.Изученные нами законы умножения применяются для упрощения вычислений.Пример. Вычислить произведение (5 • 48) • 2.Пользуясь принятым порядком действий, мы должны сначала умножить 5 на 48, а полученный результат умножить на 2.

Для упрощения вычислений применим переместительный и сочетательный законы умножения:(5 • 48) • 2г= (48 • 5) — 2 = 48 • (5 • 2) = 48 • 10 = 480.В произведении нескольких множителей можно переставлять множители и заключать их в скобки любым способом.Пример. 3 • 4 • 5 • 6 = 6 • 5 • 4 • 3,    3 • 4 • 5 • 6 = (3 • 4) • (5 • 6).По определению считают, что для любого неотрицательного числа аа • 0 = 0,0 • а = 0.Тогда равенства а • b=b • а и (а • b) • с=а • (b • с) верны и для неотрицательных чисел.Например, 5 • 0 = 0 • 5, (5 • 3) • 0 = 5 • (3 • 0).

Деление

Пусть а и b—натуральные числа и а больше или равно 6 (а ≥ b). Говорят, что а делится на 6 нацело, если существует натуральное число с, произведение которого на b равно a:

а = с • b.

При этом пишут а : b = с и называют а делимым, b—делителем, с—частным. Таким образом, (a:b) • b = a, т. е. если а разделить на b и результат умножить на b, то получится а.Любое натуральное число а делится на 1 и само на себя:a : 1= a, а : а= 1,так как a • 1=а, 1 • а = а.Например, 15 делится на 1 и 15, а также на 3 и 5, а 19 делится только на 1 и само на себя. Считают также, что 0 : b = 0 для любого натурального числа b, так как 0 • b=0.Но делить на 0 нельзя. Для любого натурального числа а не существует такого числа с, чтобы выполнялось равенство a : 0 = c, так как с • 0 = 0.При делении 0 на 0 можно было бы считать, что 0:0 = с, потому что с • 0=0. Но в этом случае частным могло бы быть любое число с

Поэтому считают, что и 0 нельзя делить на 0.Отметим, что частное неотрицательных чисел а и b ( b ≠ 0)—единственное число.Отметим важное свойство частного: делимое и делитель можно умножить или разделить на одно и то же натуральное число—частное от этого не изменится

Например, 48:24 = 2 и (48-2):(24-2) = 96:48 = 2.Это свойство часто используют для упрощения вычислений 168:42=(168:3): (42:3)=56:14=(56:7): (14:7)=8:2=4Таким образом, верны формулыа:b = (а • n):(b • n), а:b = (а:n):(b:n),

где n натуральное число и во второй формуле а и b делятся на n.Докажем первую из них. Пусть а:b = с; тогда с • b = а но тогда (а • n):(b • n) также равно с, потому что с • (b • п)= (с • b) • n = а • n.    ‘

Связь деления с умножением, сложением и вычитанием

Деление — это математическая операция, имеющая определенную связь с умножением, сложением и вычитанием как с основными математическими операциями.

Деление считается полной противоположностью умножения. Произведением множителей на один из них можно найти недостающий множитель.

Пример 1

а*б=20

20 : 4 = 5

20:5 = 4

а = 4

б = 5

По принципу действия делением называется вычитание одного и того же числа, повторяющееся n раз в зависимости от величины делимого и делителя.

Пример 2

28:7=4

28-7=21, 21-7=14, 14-7=7, 7-7=0

Деление не имеет прямого отношения к операции сложения. Это отношение имеет операцию умножения, прямо противоположную операции деления.

Пример 3

3*4=12=4+4+4

12:4=3

12:3=4

Сложение натуральных чисел.

Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.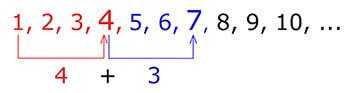Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.

Сумма — это сложение чисел. Знак  плюс “+”.В буквенном виде этот пример будет выглядеть так:

a+b=c

Компоненты сложения:a — слагаемое, b — слагаемые, c – сумма.Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:

4+3=3+4

Называется такое свойство слагаемых переместительным законом сложения.

Общие сведения

Сложение — математическая операция, при помощи которой происходит увеличение исходного числа на определенное значение. Ее элементами являются минимум два слагаемых и результат. Последний называется суммой. Всего существуют два закона сложения. К ним относятся следующие:

Коммутативный. Ассоциативный.

Первый еще называется переместительным, а второй — сочетательным. Многие школьники путают правила сложения и умножения. Следует отметить, что для последнего предусмотрены три закона, т. е. распределительный, сочетательный и переместительный. У деления и умножения правила похожи, а вот для вычитания, как и для сложения, предусмотрено также два свойства.

Свойство деления нуля на натуральное число.

Мы приняли условность, что число нуль (напомним, что нуль не относится к натуральным числам) означает отсутствие чего-либо. Таким образом, деление нуля на натуральное число – это есть деление «ничего» на несколько частей. Очевидно, что в каждой из полученных частей также будет «ничто», то есть нуль. Итак, 0:a=0

, где a
– любое натуральное число.

Полученное выражение представляет собой буквенную запись свойства деления нуля на натуральное число, которое формулируется так: результатом деления нуля на произвольное натуральное число является нуль
.

К примеру, 0:105=0
, а частное от деления нуля на 300 553
тоже равно нулю.