Гипербола в Эксель (Excel) — как построить?
См. ответ на вопрос про параболу в Эксель. Единственная разница — в функции, по которой определяется значение У. Для гиперболы формула имеет общий вид У = к / Х, и, соответственно, эта функция будет иметь разрыв при Х = 0, что нужно учитывать при задании диапазона для Х. Диапазонов может быть два — например, от -10 до -1 и от 1 до 10 с шагом 0,1 каждый. Формула, например, =3/A2.
График нужно будет построить сначала для одного из диапазонов, потом — щелкнуть правой кнопкой на линии графика, выбрать пункт «Выбрать данные» и нажать кнопку «Добавить», выбрав второй диапазон данных, после чего щелкнуть уже на второй линии, выбрав для нее тот же цвет и толщину, что и для первой линии, чтобы казалось, что график один.
Впрочем, можно поступить и проще — построить график сразу для всего диапазона, после чего удалить значения в ячейках из его середины (для Х = -1 и Х = 1). Внешне результат не изменится.
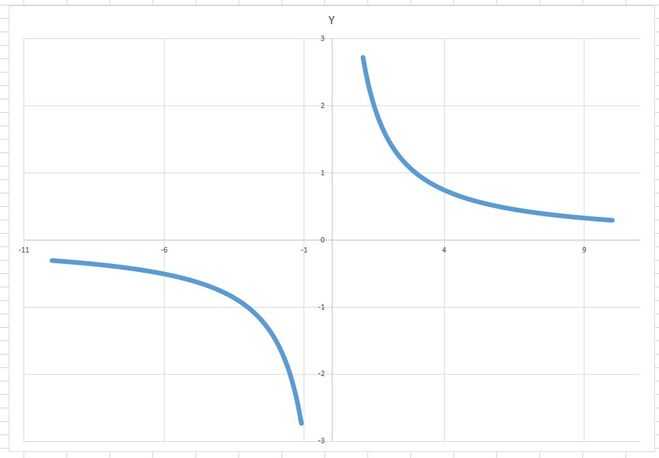
Построение гиперболы, на самом деле, очень простое занятие, если знать как, ведь для этого нужно построить массив значений гиперболы.
Для этого приходится брать произвольные значения Х, кроме того, когда знаменатель стремится к нулю, но не слишком близко к нулю. Затем, с помощью формулы установите значения У и растяните их, скопировав эту нужную формулу и получив, таким образом, значения У. Затем остаётся выделить получившийся диапазон значений Х и У, а затем выбрать во вкладке графика соответствующий вашим потребностям график. Мне лично нравится точечная диаграмма, но можно выбрать и график. Затем остаётся посмотреть на получившуюся диаграмму и добавить или убрать x-значения или заменить их другими.
Получите точки, согласно которым график будет построен. Обозначьте два столбца, у одного должно быть значение Х, у второго у. В первый столбец введите данные от -7 до 7, с шагом 1, но исключите ноль. Там где должен быть 0 следует оставить ячейку пустой.
После в ячейке В2 следует прописать формулу: «=1/A2». После, ее скопируйте на оставшиеся ячейке, пустую строку не трогайте. Получатся готовые данные для построения гиперболы.
После, следует выделить область со значением, также пустую строку. Зайдите на верхней панели во вкладку Вставка, выберите Точечная среди возможных графиков. Выберите второй график.
Получился график гиперболы, который можно оформить, прописав оси и функцию.
Для прописания осей, на панели Вставка найдите с правой стороны блок Текст. Нажмите на иконку с надписью — Надпись. При помощи курсора нажмите на любую область на графике и пропишите название оси, после перетащите в место, которое нужно для получение обоих оси.
Следует выделить надпись Ряд1 и нажать при помощи правой кнопки мыши для появления меню. В нем нужно выбрать Выбрать данные, а на экране будет новое меню. В левой части нужно выделить Ряд1, которое вы увидите и нажать на кнопку Изменить. В меню, которое появится вы сможете отредактировать название, а после можно закрыть таблицы, которые являются дополнительными.
Гипербола и обратная пропорциональность
Ранее мы уже строили графики . Однако мы рассматривали только случаи, при которых показателем в степени являлось натуральное число. Теперь же изучим функцию у = х– 1. Напомним, что по определению отрицательной степени
Найдем область определения функции у = 1/х. Ясно, что аргумент не может равняться нулю, так как иначе получим деление на ноль:
у(0) = 1:0
При любых других значениях х значение у вычислить можно, а потому областью определения будет промежуток (– ∞; 0)⋃(0;+ ∞).
При положительных значениях аргумента ф-ция также будет положительной:
у(5) = 1:5 = 0,2
у(2) = 1:2 = 0,5
у(10) = 1:10 = 0,1
При отрицательных х величина у будет становиться отрицательной:
у(– 5) = 1:(– 5) = – 0,2
у(– 2) = 1:(– 2) = – 0,5
у(– 10) = 1:(– 10) = – 0,1
Это означает, что график ф-ции будет располагаться в I и III четвертях.
Можно заметить, что чем больше х, тем ближе у к нулю:
у(1) = 1
у(10) = 0,1
у(100) = 0,01
И наоборот, чем ближе х к нулю, тем больше у:
у(0,1) = 1:0,1 = 10
у(0,01) = 100
у (0,001) = 1000
При этом у не может равняться нулю. Действительно, дробь равна нулю только тогда, когда ее числитель равен нулю. Однако варьируя х, мы меняем только знаменатель, а в числителе остается единица. Поэтому областью значений функции у = х– 1 является промежуток (– ∞; 0)⋃(0;+ ∞).
Для построения графика найдем некоторые точки графика и занесем их в таблицу. Мы построим две таблицы – одну для положительных х, другую для отрицательных:
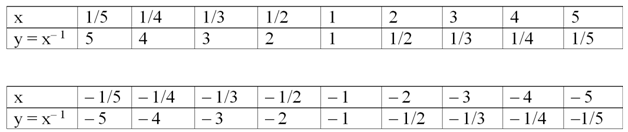
Теперь можно посмотреть и на сам график:
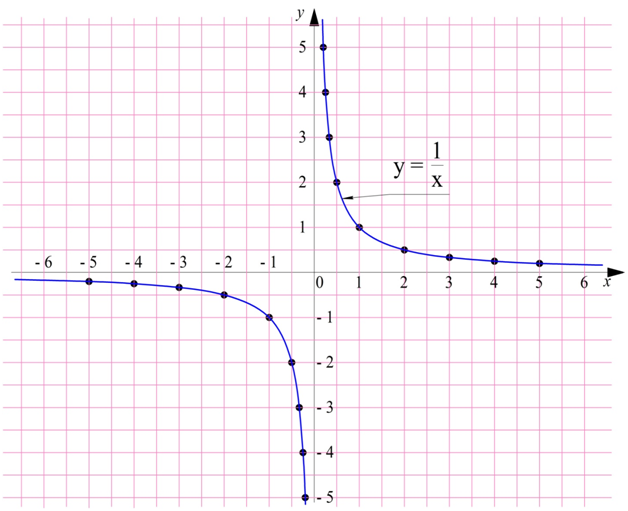
Первое, что бросается в глаза – это то, что график не представляет собой единую, непрерывную линию. Он разбит на две ветви, одна из которых располагается в III четверти, а другая – в I четверти. Такой «разрыв» связан с тем, что ноль не входит в область определения ф-ции.
Также можно заметить симметричность графика. Действительно, одна из ветвей является симметричным отображением второй ветви.
Построенный нами график называется гиперболой.
На координатной плоскости есть две прямые линии, к которым гипербола приближается, но при этом он не касается их. Это оси Ох и Оу. Для наглядности покажем их штриховой линией:
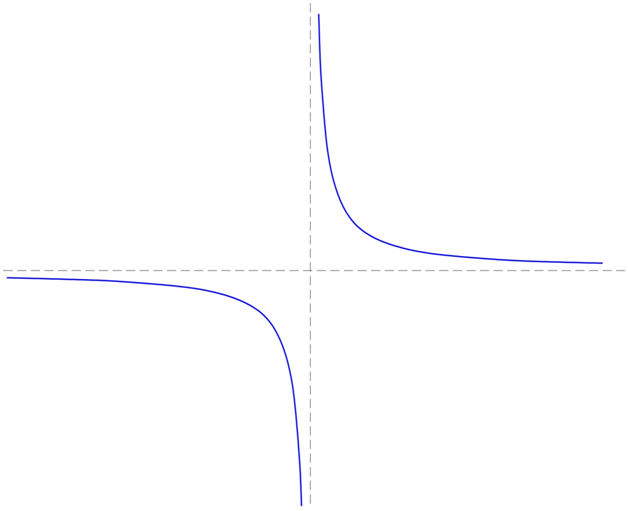
В математике подобные линии называют асимптотами функции. Горизонтальная асимптота прямая соответствует линии х = 0, а вертикальная асимптота линии у = 0.
Зная, как выглядит график у = 1/х, мы можем построить и другие, схожие с ним графики для ф-ций у = k/х, где k– это некоторое число. Их можно получить из гиперболы, используя сжатие и растяжение графиков. Если коэффициент k больше единицы, то график «отдаляется» от осей Ох и Оу:
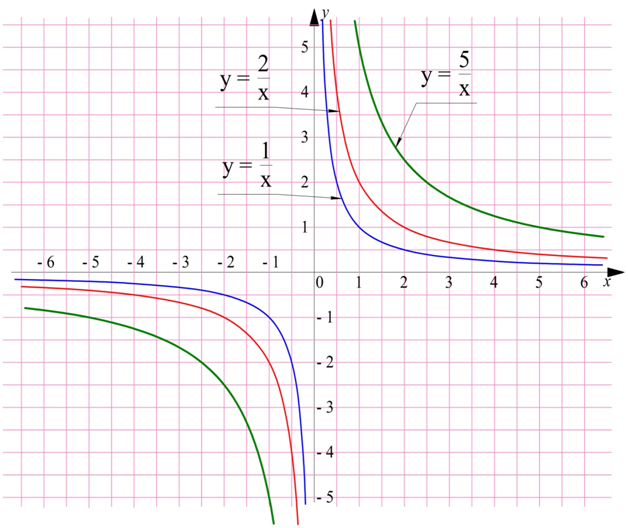
Все эти линии являются примерами гипербол. Если коэффициент k отрицательный, то графики переворачиваются относительно оси Ох и занимают II и IV четверти:
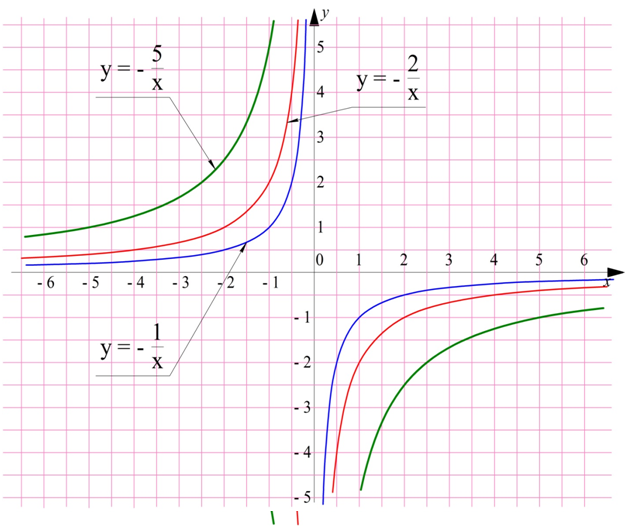
Все приведенные зависимости вида у = k/х называют обратными пропорциональностями.

Примерами обратной пропорциональности являются ф-ции:
Обратная пропорциональность очень часто встречается в жизни. Так, время, затрачиваемое на поездку на автомобиле, обратно пропорционально средней скорости движения. Количество товара, которое можно купить на одну зарплату, обратно пропорционально стоимости этого товара.
Определение гиперболы, решаем задачи вместе
Определение гиперболы. Гиперболой называется множество
всех точек плоскости, таких, для которых модуль разности расстояний от двух точек,
называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:
,
где a и b — длины
полуосей, действительной и мнимой.

На чертеже ниже фокусы обозначены как и
.
На чертеже ветви гиперболы — бордового цвета.
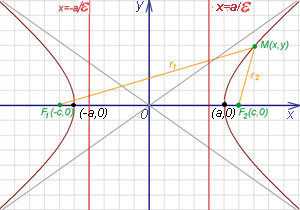
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы,
если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы
и получаем:
.
Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox)
называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на
рисунке чёрным.
Точки и
, где
,
называются фокусами гиперболы (на чертеже обозначены
зелёным, слева и справа от ветвей гиперболы).
Число
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях
относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы,
если расстояние между фокусами равно 10 и действительная ось равна 8.
Решение.
Если действительная полуось равна 8, то её половина, т. е. полуось
,
Если расстояние между фокусами равно 10, то число c из
координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется
вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:
.
Пример 3. Составить каноническое уравнение гиперболы,
если её действительная ось равна 48 и эксцентриситет .
Решение. Как следует из условия, действительная полуось
. А эксцентриситет — это пропорция и
так как , то коэффициент пропорциональности
отношения и
равен 2. Следовательно, .
Из формулы числа выражаем квадрат мнимой полуоси и
вычисляем:
.
Результат — каноническое уравнение гиперболы:
Если —
произвольная точка левой ветви гиперболы () и
—
расстояния до этой точки от фокусов , то
формулы для расстояний — следующие:
.
Если —
произвольная точка правой ветви гиперболы () и
—
расстояния до этой точки от фокусов , то
формулы для расстояний — следующие:
.
На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов
есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами гиперболы (на чертеже — прямые ярко-красного
цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы
,
где —
расстояние от левого фокуса до точки любой ветви гиперболы, —
расстояние от правого фокуса до точки любой ветви гиперболы и и —
расстояния этой точки до директрис и
.
Пример 4. Дана гипербола
.
Составить уравнение её директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется
найти эксцентриситет гиперболы, т. е. .
Вычисляем:
.
Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы
эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к
которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями
.
На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:
, где .
В том случае, когда угол между асимптотами — прямой, гипербола называется
равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её
уравнение запишется в виде ,
то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы
и координаты
точки , лежащей
на гиперболе. Составить уравнение гиперболы.
Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно,
нужно сначала найти коэффициент пропорциональности отношения .
Для этого подставляем в формулу канонического уравнения гиперболы координаты точки M
x и y и значения числителя и знаменателя из уравнения асимптоты, кроме того,
умножаем каждую дробь в левой части на коэффициент пропорциональности k.
.
Теперь имеем все данные, чтобы получить каноническое уравнение
гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим
образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после
отражения движется так, как будто он исходит из другого фокуса.
Асимптоты и фокусы гиперболы
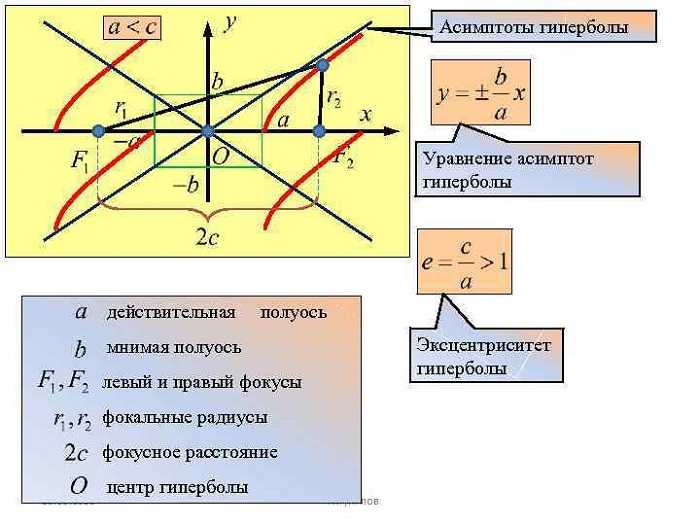
Фокус находится на оси X (с этого мы и начали). Расстояние до центра гиперболы (он же центр симметрии C) называется фокальной точкой и обозначается буквой «с». Его формула:
Умозрительно очевидно, что часть конуса состоит из двух кривых. Их называют ветвями гиперболы. Несомненно также, что ветви ограничены воображаемой поверхностью. Фокус всегда находится внутри ветвей.
Помучавшись с производными и пределами, получаем формулы асимптот (прямые, расстояние, которое от кривой стремится к нулю на бесконечном расстоянии от «0»):
Расстояние от фокуса до асимптоты называется прицельным параметром и обозначается буквой «б».
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрите рисунок и комментарии к нему.
Построим главный прямоугольник гиперболы и проведем диагонали. Если продолжить диагонали прямоугольника за границы, то получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первом квадранте, где находится график функции:
Важно учесть, что эта функция возрастает на интервале , при x = a, y = 0, и график приближается к асимптоте y = (b/a) * x снизу. Нарисуйте график:
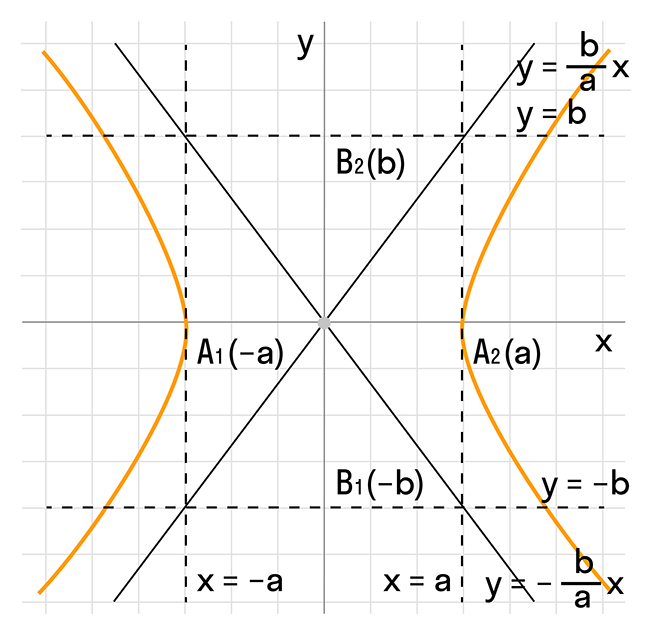
Кроме того, график, построенный в первой четверти, оказывается симметричным относительно бычьей оси, и мы получаем правую ветвь гиперболы. Теперь покажем правую ветвь гиперболы относительно оси Oy.
По определению эксцентриситет гиперболы
Зафиксируем реальную ось 2а и начнем изменять фокусное расстояние 2с.
Поскольку b^2 = c^2 — a^2, значение b изменится.
- Пусть с -> а.В этом случае ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси ox. Главный прямоугольник гиперболы выражается границей на отрезке A1A2, а сама гипербола выражается двумя лучами на оси абсцисс: (-∞; -a и </a>a; ∞).
- Пусть с -> ∞.В этом случае ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Oy. Главный прямоугольник гиперболы вытянут вдоль оси у, а ветви гиперболы приближаются к прямым х = +-а и в пределе сливаются с ними. Гипербола выражается двумя прямыми х = +-а, параллельными оси Оу.
В этом случае ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Oy. Главный прямоугольник гиперболы вытянут вдоль оси у, а ветви гиперболы приближаются к прямым х = +-а и в пределе сливаются с ними. Гипербола выражается двумя прямыми х = +-а, параллельными оси Оу.
Равносторонняя гипербола — это гипербола, эксцентриситет которой равен √2. Его еще называют равносторонним.
Из определения следует, что в равносторонней гиперболе a = b ее каноническое уравнение выглядит так: x^2 — y^2 = a^2
Фактически, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. А так как a и b положительные числа, мы получаем a = b.
Пример 1
Функция y = 4/x задана. Давайте построим это.
Решение
Поскольку k > 0, гипербола будет находиться в I и III координатных квадрантах.
Чтобы построить график, необходимо сначала создать таблицу соответствия между значениями x и y. То есть мы берем конкретное значение x, заменяем его формулой функции и получаем y.
| икс | у | Расчет у |
| 0,5 | 8 | 4 / 0,5 = 8 |
| 1 | 4 | 4/1 = 4 |
| 2 | 2 | 4/2 = 2 |
| 4 | 1 | 4/4 = 1 |
| 8 | 0,5 | 4/8 = 0,5 |
Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет обращена к осям координат. В результате получается ветвь гиперболы, расположенная в первой четверти.
Для построения ответвления в третьем квартале вместо x подставляем в формулу -xi. Вот как мы вычисляем значения y.
| икс | у | Расчет у |
| -0,5 | -8 | 4 / -0,5 = -8 |
| -1 | -4 | 4 / -1 = -4 |
| -2 | -2 | 4 / -2 = -4 |
| -4 | -1 | 4/-4 = -1 |
| -8 | -0,5 | 4/-8 = -0,5 |
Соединив полученные точки, получим следующий результат. На этом построение гиперболы завершено.
Пример 2
Приведенный выше пример был одним из самых простых (без изменения асимптот). Усложним задачу и построим гиперболу, заданную функцией ниже:
Решение
Поскольку k < 0, график будет помещен во вторую и четвертую четверти.
Теперь определим асимптоты, в нашем случае это x = 3 и y = 4 (об их сдвигах см информацию выше).
Создадим таблицу соответствия между значениями x и y.
| х II кв. | у II кв. | х IV кв. | у IV кв. |
| -1 | 4,5 | 3,5 | |
| 1 | 5 | 4 | 2 |
| 2 | 6 | 5 | 3 |
| 2,5 | 8 | 7 | 3,5 |
Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: \( \displaystyle v=\frac{S}{t}\), где \( v\) – скорость, \( t\) – время в пути, \( S\) – расстояние (путь).
Отсюда можно выразить время: \( \displaystyle t=\frac{S}{v}\)
Пример:
Человек едет на работу со средней скоростью \( 40\) км/ч, и доезжает за \( 1\) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью \( 60\) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
\( \displaystyle 60\) км/ч – \( 60\) мин.\( \displaystyle 60\) км/ч – \( x\) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
\( \displaystyle \frac{40}{x}=\frac{60}{60}\text{ }\Rightarrow \text{ }x=40\)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
\( \displaystyle t\left( v \right)=\frac{S}{v}\).
Известно, что \( t\left( 40 \right)=60\), тогда:
\( \frac{S}{40}=60\text{ }\Rightarrow \text{ }S=40\cdot 60=2400\).
Нужно найти \( t\left( 60 \right)\):
\( \displaystyle t\left( 60 \right)=\frac{2400}{60}=40\) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Калькулятор онлайн — Построение графика дробно-линейной функции (гиперболы) (с подробным решением)
Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.
Эта математическая программа для построения графика дробно-линейной функции (гиперболы) сначала делает преобразование вида $$ y= frac{ax+b}{cx+d} ;
ightarrow ; y= frac{k}{x+p} +q $$ а затем последовательно строит графики функций: $$ y= frac{1}{x} $$ $$ y= frac{k}{x} $$ $$ y= frac{k}{x+p} +q $$
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода дробно-линейной функции, рекомендуем с ними ознакомиться.
Правила ввода дробно-линейной функции В качестве переменной можно использовать только x Все остальные буквы недопустимы. При вводе можно использовать только целые числа. Преобразовать Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь. Через несколько секунд решение появится ниже.
Пожалуйста подождите сек…
Наши игры, головоломки, эмуляторы: Игра «iChart»Создание островаЭмуляторгравитацииГоловоломка «SumWaves»
Любую дробно-линейную функцию ( y=frac{ax+b}{cx+d} ) с помощью элементарных алгебраических преобразований можно записать в виде ( y = frac{k}{x+p} +q, ) где ( k= frac{bc-ad}{c^2}, quad p=frac{d}{c}, quad q=frac{a}{c} )
Графиком функции ( y = frac{k}{x+p} +q ) является гипербола, получаемая сдвигом гиперболы ( y = frac{k}{x} ): вдоль оси абсцисс влево на p, если p > 0, вправо на |p|, если p
Применение гиперболических функций в науке и технике
Физика и инженерия
Гиперболические функции играют ключевую роль во многих областях науки и техники. Они используются, например, при решении задач, связанных с движением тел в поле силы тяжести и в электромагнитных полях. Гиперболические функции также помогают смоделировать поведение гибких материалов и исследовать лазерные процессы в оптике.
Экономика и финансы
Гиперболические функции применяются в экономике и финансах при анализе кредитных рисков, планировании инвестиций и менеджменте риска. Например, такие функции позволяют оценить долгосрочные движения цен на акции и другие финансовые инструменты.
Криптография и безопасность
Гиперболические функции также играют важную роль в криптографии и защите данных. Они используются, например, для построения безопасных хэш-функций, которые используются для проверки целостности данных и идентификации пользователей.
Заключение
Все перечисленные примеры лишь малая часть областей, в которых гиперболические функции находят свое применение
Изучение этих функций особенно важно для студентов, готовящихся к карьерам в науке, технике, экономике и других областях, где необходимо оперировать математическими понятиями и моделировать реальные явления
Создание графиков гиперболических функций в Excel
Шаг 1: Открыть новую книгу Excel
Перед началом создания графика гиперболической функции необходимо открыть новую книгу Excel и выбрать лист, на котором будет создаваться график. Для этого нажмите на кнопку «Новая книга» и выберите нужный лист.
Шаг 2: Вбить формулу функции
Для создания графика гиперболической функции необходимо ввести формулу в ячейку. Например, функция гиперболического косинуса имеет вид: =COSH(A1), где A1 — ячейка, в которой указывается значение аргумента функции.
Шаг 3: Создание графика
После ввода формулы гиперболической функции и выбора нужного диапазона значений аргумента необходимо выбрать тип графика, на который будет отображаться функция. Для этого нажмите на кнопку «Вставка» и выберите «Диаграммы» в меню. Затем выберите тип графика и нажмите «ОК».
Шаг 4: Дополнительные настройки графика
Для улучшения визуальной структуры графика можно добавить название осей, легенду, изменить цвет линии и толщину. Для этого перейдите во вкладку «Рисование» и выберите нужные настройки.
Создание графика гиперболической функции в Excel достаточно просто и может быть выполнено даже начинающими пользователями.
Гипербола. График функции и свойства.
теория по математике функции
Графиком функции у= k x . . , где k ≠ 0 число, а х – переменная, является кривая, которую называют гиперболой.
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
Свойства гиперболы (у= k x . )
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
- Область определения – любое число, кроме нуля.
- Область значения – любое число, кроме нуля.
- Функция не имеет наибольших или наименьших значений.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Построить график функции у= 10 x . . .
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.
Теперь для построения гиперболы соединим точки плавной линией. Построить график функции у= − 5 x . . .
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у
При делении обращаем внимание на знаки, чтобы не допускать ошибок
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
Установите соответствие между графиками функций и формулами, которые их задают.
1) y = x²
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Способы задания функций
Аналитическое задание функции.
Функция задана аналитически, если функциональная зависимость выражена
в виде формулы, которая указывает совокупность тех математических операций, которые
должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение
функции.
При аналитическом задании функции указывают область определения, либо
не указывают. В первом случае функция задаётся в виде
,
где — область определения функции, во втором случае —
в виде .
Во втором случае областью определения функции считается наибольшее множество, на котором
имеет смысл формула, которой задана функция, то есть наибольшее множество аргумента, которое
приводит к действительным значениям функции.
Важно, что функцию не следует отождествлять с формулой, с помощью
которой она задана. Например, функции и
,
выраженные одной и той же формулой ,
так как они имеют разные области определения
Наоборот, одна и та же функция может быть задана разными формулами на
различных участках области определения. Пусть, например,
Здесь две формулы задают одну функцию, определённую на всей числовой
прямой. При значения этой функции
определяются по первой формуле, а при — по
второй.
Пример 3. Площадь круга вычисляется как функция
радиуса .
Каковы должны быть требования к аналитическому заданию этой функции, то есть, можно ли
записывать без
указания области определения функции или же нужно указывать область определения и записывать
?
Решение. Нельзя опускать запись области определения функции
, так как
хотя выражение имеет
смысл при всех действительных значениях , но для
площади круга допустимы лишь значения .
Аналитический способ задания функции удобен тем, что значения функции
можно вычислить при любых значениях аргумента. Недостатком этого способа задания функции
является его малая наглядность.
Графический способ задания функции
График функции даёт наглядное представление о её свойствах. Например,
график линейной функции
— прямая линия, график квадратичной функции —
парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде
формул или уравнений. Таким образом, под графиком функции понимается множество точек
плоскости, декартовы координаты которых удовлетворяют заданному уравнению.
Графический способ задания функции помимо геометрического изображения
функции, заданной уравнением, удобен тогда, когда функцию трудно задать аналитически.
Задать функцию графически — это значит построить её график. Это часто делают самопишущие
приборы. Например, в медицине электрокардиограф строит электрокардиограмму — кривую
изменения электрических импульсов сердечной мышцы.
Графиком числовой функции
называется множество точек плоскости с координатами ,
абсциссы которых — числа из области определения функции, а ординаты — соответствующие значения
функции.
Не всякое множество точек координатной плоскости, даже не всякая линия
может служить графиком функции. Линия только в том случае задаёт функцию, если любая прямая,
параллельная оси , пересекает её не более чем в
одной точке.
Пример 4. На рисунке ниже — график параболы,
заданной уравнением .
Является ли этот график графиком функции?
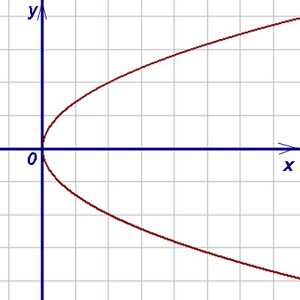
Решение. График параболы, заданной уравнением ,
не является графиком функции, поскольку прямая, параллельная оси ,
пересекает его в двух точках при всех значениях ,
кроме . Заданное уравнение
эквивалентно двум уравнениям ,
каждое из которых определяет функцию. Графиком функции
служит верхняя половина параболы, а графиком функции —
её нижняя половина.
Табличный способ задания функции
При табличном способе задания функции рядом с числовым значением аргумента
записывается соответствующее значение функции. Широко известных таблицы квадратов и кубов
чисел, квадратных корней, то есть таблицы функций ,
,
.
Недостатком табличного способа задания функции является то, что в
таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности
изменения функции при этом могут быть искажены или утрачены.
Гиперболические функции
Гиперболические функции
Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Основные понятия:
Рассмотрим единичную окружность с центром в начале координат, уравнение которого имеет вид х 2 + у 2 = 1.
Согласно определению, синусом угла называют ординату у точки А(х, у) единичной окружности, а косинусом — абсциссу х этой же точки (рис. 1)
Докажем, что площадь сектора АОВ равна числовому значению угла AOD, взятом в радианах.
Действительно, если R=1, а угол сектора АОВ- то
Следовательно, в тригонометрических функциях за аргумент можно принимать не только угол, а и площадь соответствующего сектора.
Рассмотрим теперь равнобокую гиперболу с асимптотами , уравнение которой имеет вид
Повторим предыдущие рассуждения:
– выберем на гиперболе т. А(х, у);
– проведём радиусы ОА и ОВ ().
Образовавшуюся фигуру OANB называют гиперболическим сектором (сектором ),
абсциссу точки А – гиперболическим косинусом;
ординату точки А – гиперболическим синусом.
Возьмём за аргумент площадь гиперболического сектора . Получим:
Найдём площадь гиперболического сектора, как разность площади треугольника АОВ и криволинейной трапеции ANB.
Потому, что фигура симметрична, имеем
либо, решив систему
Аналогично как в тригонометрии вводят понятия тангенса и котангенса
Свойства гиперболических функций
Чётность и нечётность проверим подставив (-х) в соответствующие формулы
Следовательно, как и в тригонометрических функциях, имеем чётная, а нечётные.
Остальные свойства легко установить построив графики гиперболических функций.
Для построения воспользуемся записью
то есть графики функций
Полученные графическим сложением ординат графики функций имеют вид:
Графики следующие
Видим, что в отличии от тригонометрических, гиперболические функции непериодические. Основные свойства каждой из гиперболических функций указаны в опорном конспекте (п. 10.5).
Переход от гиперболических функций к тригонометрическим и наоборот
Используя гиперболические функции можно вывести формулы Эйлера. Действительно, вспомним разложение в ряд Маклорена функций
Положим в разложении функции у=е х за аргумент х=zj. Получим:
Учитывая, что где будем иметь:
Именно эти формулы позволяют установить зависимость между тригонометрическими и гиперболическими функциями.
Принимаем без доказательств, что все тригонометрические формулы действительны и для воображаемого аргумента. Это предположение позволит установить зависимость между гиперболическими функциями.
Аналогично можно получить формулы для
Присылайте задания в любое время дня и ночи в ➔
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Обратная пропорциональность — коротко о главном
Определение:
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
\( D\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или, что то же самое, \( D\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\)
\( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или \( E\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент \( \displaystyle k\)
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график:
Коэффициент \( \displaystyle a\)
Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).
Коэффициент \( b\)
Число \( b\) отвечает за смещение графика функции вверх на величину \( b\), если \( b>0\), и смещение вниз, если \( b<0\).
Алгоритм построения графика функции \( \displaystyle y=\frac{k}{x-a}+b\)
- Определяем коэффициенты \( \displaystyle k\), \( \displaystyle a\) и \( \displaystyle b\).
- Строим график функции \( \displaystyle y=\frac{k}{x}\) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на \( \displaystyle a\). Но проще двигать не график, а оси, так что ось \( \displaystyle Oy\) сдвигаем влево на \( \displaystyle a\).
- График должен быть сдвинут вверх на \( \displaystyle b\). Но проще двигать не график, а оси, так что ось \( \displaystyle Ox\) сдвигаем вниз на \( \displaystyle b\).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.






























