Что такое линейная функция: определение, формула, график

Линейная функция

Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.

То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).

Что значит «допустимому»?

Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.

Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.

Ну и вернемся, наконец, к теме данной статьи.

Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.

Как думаешь, почему она называется линейной?

Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.

Исследование функции

Важные моменты на графике функции y = f(x):

• стационарные и критические точки;
• экстремальные точки;
• нулевые функции;
• точки останова функций.

Стационарные точки — это точки, в которых производная функции f(x) равна нулю.

Критические точки — это точки, в которых производная функции f(x) равна нулю или не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — это максимальное или минимальное значение функции в заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Следовательно, при достижении минимума точка экстремума называется точкой минимума, а при достижении максимума — точкой максимума.

Нули функции — это значения аргумента, при которых значение функции равно нулю.

Асимптота – это прямая, обладающая таким свойством, что расстояние от точки до графика функции до этой прямой стремится к нулю при неограниченном расстоянии от начала координат до точки графика. По способам их нахождения различают три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, говорят, что f(x) имеет разрыв в этой точке.

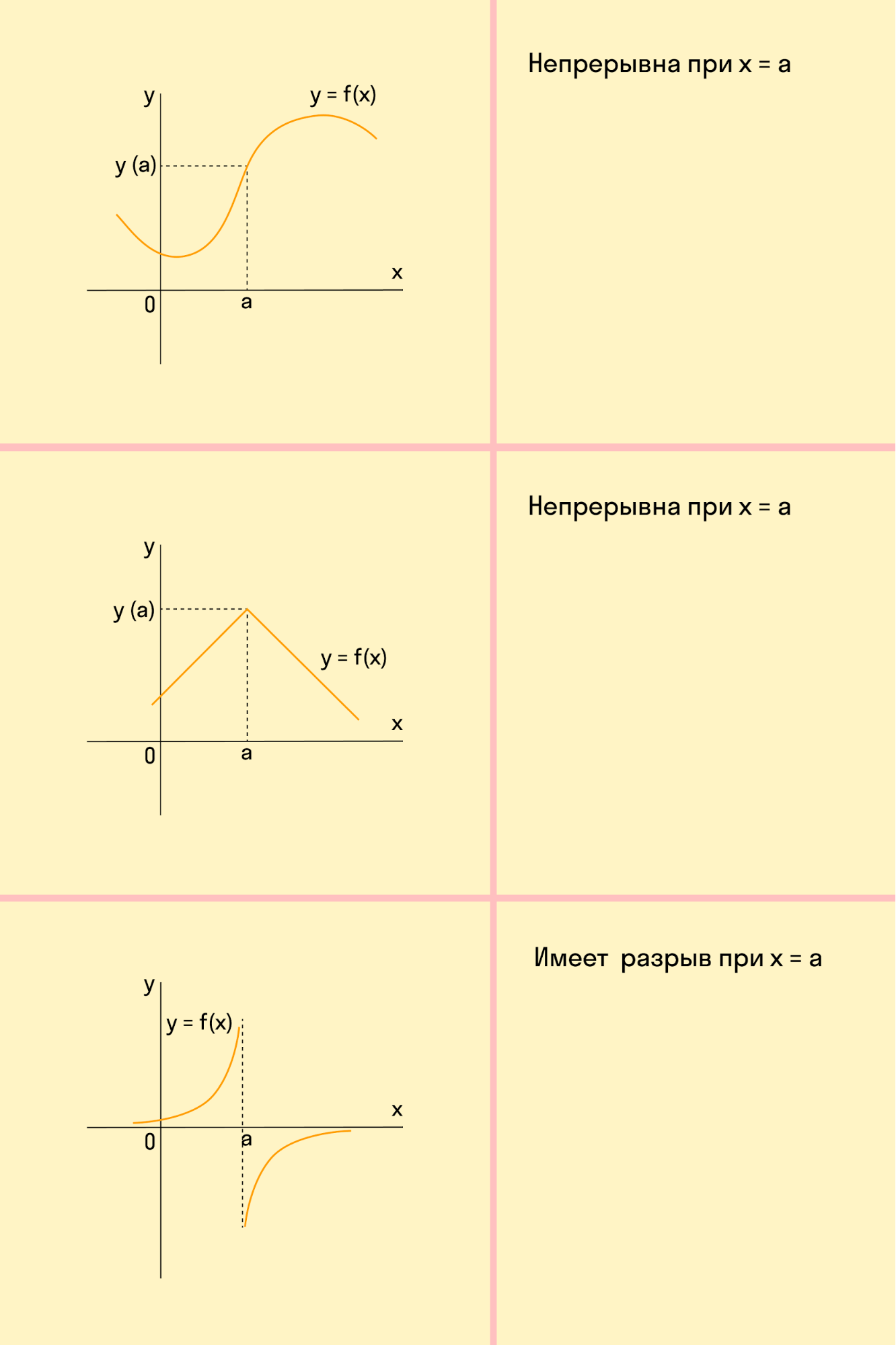
Если нам необходимо построить график неизвестной функции, когда невозможно заранее представить форму графика, полезно использовать схему для изучения свойств функции. Это поможет вам получить представление о графике и начать построение по точкам.

Схема построения графика для функции:

1. Найдите диапазон функции.
2. Найдите диапазон допустимых значений функции.
3. Проверьте, является ли функция четной или нечетной.
4. Проверьте, является ли функция периодической.
5. Найдите точку пересечения с осью OY (если есть).
6. Вычислить производную и найти критические точки, определить интервалы возрастания и убывания.
7. Знаковые интервалы.
8. Асимптоты.
9. На основании проведенного исследования постройте график функции.

Бывают ли зеленые розы — кто их вывел

Зеленая роза пришла из Голландии. Изначально она обитала в дикой природе, где и была замечена ученым-ботаником Майером. Тогда он решил самостоятельно воссоздать данный вид, для этого соединил белую розу и колючий терновник.

Зеленая роза

Полученный гибрид получил особое название — роза чайно-гибридная зеленая. Его описание было опубликовано во многих ботанических журналах и уже скоро цветок стал известен в каждом уголке планеты.

В настоящее время роза имеет широкое распространение по всему миру. Это обусловлено ее уникальными особенностями, к которым относят:

• Цвет. Бутоны имеют уникальный светло-зеленый оттенок.
• Форма куста преимущественно раскидистая.
• Высота взрослого растения может быть от 30 до 60 сантиметров в зависимости от сорта.
• Размер бутонов может быть от 5 до 10-15 сантиметров в зависимости от сорта, условий произрастания.
• Цветки бывают одиночные или в соцветиях.
• Лепестки могут быть обычные или махровые.

Единственное — данный вид не имеет запаха, присущего обычным розам. Но все компенсируется невероятно красивым внешним видом.

Как найти формулу линейной функции по графику?

Если на рисунке изображён график линейной функции, то можно определить её формулу, используя информацию о двух точках на графике. Для этого необходимо найти координаты этих точек и использовать их значения для нахождения углового коэффициента и свободного члена линейной функции.

Первым шагом следует выбрать две точки на графике. Чем ближе точки к началу координат, тем проще будет найти их координаты. Иногда на графике уже указаны значения координат, но если нет, то можно определить их приближенно, используя масштаб и деления осей координат.

После определения координат двух точек, можно использовать их значения для нахождения углового коэффициента прямой. Идея заключается в вычислении изменения «у» (значение функции) при изменении «х» (аргумента). Для этого нужно разделить разность значений «у» на разность значений «х». Полученное значение будет угловым коэффициентом (наклоном) прямой. Он обозначается символом «k».

После вычисления углового коэффициента можно использовать любую из двух точек для определения свободного члена линейной функции. Для этого можно воспользоваться формулой прямой: y = kx + b, где «b» — свободный член. Подставив известный угловой коэффициент и координаты одной из точек в эту формулу, можно вычислить значение свободного члена «b».

Таким образом, зная угловой коэффициент и свободный член линейной функции, можно написать её формулу по графику.

Использование точек на графике

На рисунке изображён график линейной функции. Для того чтобы написать по нему формулу, необходимо использовать точки на графике. Каждая точка представляет собой пару значений (x, y), где x — значение независимой переменной, а y — значение зависимой переменной.

Найти формулу линейной функции можно, зная координаты двух точек на графике. Для этого можно использовать метод нахождения уравнения прямой через две точки. Зная координаты точек (x₁, y₁) и (x₂, y₂), можно найти угловой коэффициент (наклон) прямой:

k = (y₂ — y₁) / (x₂ — x₁)

Далее, используя значение углового коэффициента, можно найти значение коэффициента b (смещение) с помощью одной из формул:

• Если известна точка (x₁, y₁): b = y₁ — k * x₁
• Если известна точка (x₂, y₂): b = y₂ — k * x₂

Итак, получив значения углового коэффициента k и коэффициента смещения b, можно записать уравнение прямой в виде:

y = kx + b

Таким образом, использование точек на графике линейной функции позволяет найти её уравнение и описать зависимость между переменными, как изображено на рисунке.

Работа с угловым коэффициентом

Для линейной функции, график которой изображён на рисунке, можно написать формулу, используя угловой коэффициент. Угловой коэффициент определяет наклон прямой на графике, а также задаёт зависимость между изменением значения функции и изменением значения аргумента.

Чтобы найти угловой коэффициент, достаточно выбрать две точки на графике и воспользоваться формулой:

m = (y2 — y1) / (x2 — x1)

где m — угловой коэффициент, (x1, y1) и (x2, y2) — координаты выбранных точек.

Найденный угловой коэффициент позволяет написать формулу линейной функции вида:

y = mx + b

где y — значение функции, x — аргумент функции, m — угловой коэффициент, b — свободный член, который определяет смещение линии относительно оси ординат.

Таким образом, зная график линейной функции и используя угловой коэффициент, можно записать формулу этой функции и использовать её для решения задач, анализа и прогнозирования.

Использование точки пересечения с осью ординат

На рисунке изображён график линейной функции. Для того чтобы написать формулу этой функции, можно использовать точку пересечения графика с осью ординат.

Точка пересечения с осью ординат представляет собой точку, в которой график функции пересекает вертикальную ось. Это означает, что при задании значения аргумента равного нулю, соответствующее значение функции также будет равно нулю.

Для определения коэффициента при переменной x в формуле линейной функции, нужно знать координаты точки пересечения с осью ординат.

Предположим, что точка пересечения с осью ординат имеет координаты (0, b). Тогда формула линейной функции будет иметь вид y = kx + b, где k — коэффициент при x, а b — значение функции при x = 0.

Таким образом, если на графике известна точка пересечения с осью ординат, можно легко записать формулу линейной функции.

Определение линейной функции

Линейная функция — это математическая функция, которая может быть представлена в виде уравнения вида y = ax + b, где x и y — переменные, a — коэффициент наклона, b — свободный член.

Линейная функция представляет собой прямую на координатной плоскости. Коэффициент наклона a определяет, насколько быстро функция меняется по оси y при изменении x. Если а > 0, то функция возрастает; если а

Линейная функция имеет простую геометрическую интерпретацию. Если мы представим x и y как координаты точек на плоскости, то каждая пара значений (x, y) определяет точку на прямой. Таким образом, линейная функция связывает две переменные в простом и понятном математическом отношении.

Примеры линейных функций:

• y = 2x + 3
• y = -0.5x + 1
• y = 5x — 2

Как по графику определить коэффициент k?

1. Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
2. Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:

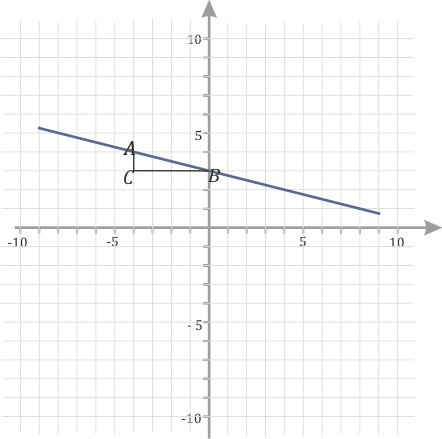
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).

Применение линейных функций в реальной жизни

Линейные функции являются одними из базовых математических моделей, используемых для описания различных явлений в реальной жизни. Эти функции имеют простую формулу вида y = kx + b, где k и b — константы, а x и y — переменные.

Применение линейных функций можно встретить во многих областях, таких как физика, экономика, инженерия и многих других. Давайте рассмотрим несколько примеров.

1. Физика

В физике линейные функции используются для описания многих явлений. Например, закон Ома в электричестве, который описывает зависимость тока от напряжения в цепи, является линейной функцией. Также можно использовать линейные функции для моделирования скорости движения тела, связи между силой и ускорением и многое другое.

2. Экономика

В экономике линейные функции могут использоваться для анализа зависимости между двумя переменными. Например, функция спроса на товар может быть линейной функцией, где спрос на товар зависит от его цены. Также линейные функции могут быть использованы для моделирования доходности, расходов и других экономических показателей.

3. Инженерия

В инженерии линейные функции применяются в различных областях. Например, они используются для моделирования аналоговых электрических цепей, анализа прочности конструкций, оптимизации производственных процессов и т.д. Линейные функции также используются в системах управления, где они помогают предсказывать поведение системы при изменении входных параметров.

Это лишь несколько примеров применения линейных функций в реальной жизни. Однако, благодаря своей простоте и широкому применению, линейные функции остаются важным инструментом в математике и ее приложениях.

Что такое линейная функция?

На рисунке изображён график линейной функции. Линейная функция — это функция, график которой представляет собой прямую линию на координатной плоскости. В общем виде линейная функция может быть записана в виде y = kx + b, где x и y — переменные, k — коэффициент наклона прямой, а b — свободный член.

Как написать формулу линейной функции по графику? Для этого нужно определить коэффициент наклона и свободный член прямой. Коэффициент наклона можно найти, вычислив отношение изменения значения функции к изменению значения аргумента в двух точках на графике. Свободный член можно найти, подставив значения координат одной из точек на графике в уравнение y = kx + b и решив полученное уравнение относительно b.

Например, если на графике линейной функции две точки имеют координаты (1, 2) и (3, 4), то коэффициент наклона равен (4 — 2) / (3 — 1) = 1 и свободный член можно найти, подставив значения координат одной из точек в уравнение y = kx + b: 2 = 1 * 1 + b. Решив это уравнение, получим b = 1.

Таким образом, формула линейной функции по графику будет выглядеть следующим образом: y = x + 1.

Определение линейной функции

Линейная функция — это функция, которая задается простой алгебраической формулой. Такая функция имеет график в виде прямой линии.

Если на рисунке изображен график линейной функции, то можно по нему написать соответствующую формулу. Для этого необходимо знать координаты двух точек, через которые проходит график.

Прямая линия, изображенная на графике, имеет уравнение вида y = kx + b, где k и b — это числовые коэффициенты, которые определяют наклон и смещение линии.

Чтобы найти коэффициенты k и b, необходимо использовать значения координат двух точек. Затем можно подставить эти значения в уравнение y = kx + b и решить систему уравнений для определения k и b.

Определение линейной функции и написание ее формулы по графику весьма полезны при решении различных задач, связанных с анализом данных и построением моделей.

Линейная функция в графическом представлении

На рисунке изображён график линейной функции. График линейной функции представляет собой прямую линию, которая проходит через две точки на плоскости. Как правило, эти точки соответствуют значению переменной x и функции y от этого значения. Линейная функция имеет вид y = kx + b, где k — коэффициент наклона прямой, а b — коэффициент смещения прямой по вертикали.

Если на рисунке изображена прямая, проходящая через точки (x1, y1) и (x2, y2), то можно определить коэффициенты k и b. Коэффициент наклона прямой находится как отношение изменения значения y к изменению значения x, то есть k = (y2 — y1) / (x2 — x1). Коэффициент смещения b можно найти, подставив значения x и y одной из точек в уравнение прямой.

Например, если на рисунке изображена прямая, проходящая через точки (2, 3) и (5, 7), то коэффициент наклона прямой равен (7 — 3) / (5 — 2) = 4 / 3. Чтобы найти коэффициент смещения b, подставим значение точки (2, 3) в уравнение прямой: 3 = (4 / 3) * 2 + b. Отсюда следует, что b = 3 — (4 / 3) * 2 = -1 / 3. Таким образом, уравнение прямой будет y = (4 / 3) * x — 1 / 3.

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)

Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.

Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики. На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях). Мы рассмотрим: 

• степенную функцию (линейную, квадратичную, обратную зависимость, корни), 
• тригонометрические и обратные тригонометрические, 
• показательную и 
• логарифмическую функции.

Преобразования графиков функций. ЕГЭ 18. Задачи с параметром.

Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль? 

Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?

 Можно! И на этом уроке мы научимся производить такие трансформации. 

Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.

Построение графика функции

Чтобы понять, как строить графики функций, давайте потренируемся на примерах или воспользуемся онлайн-симулятором.

Упражнение 1. Построим график функции

Как мы решаем:

Упростим формулу функции:

при х ≠ -1.

График функции представляет собой прямую линию y = x — 1 с пробитой точкой M (-1; -2).

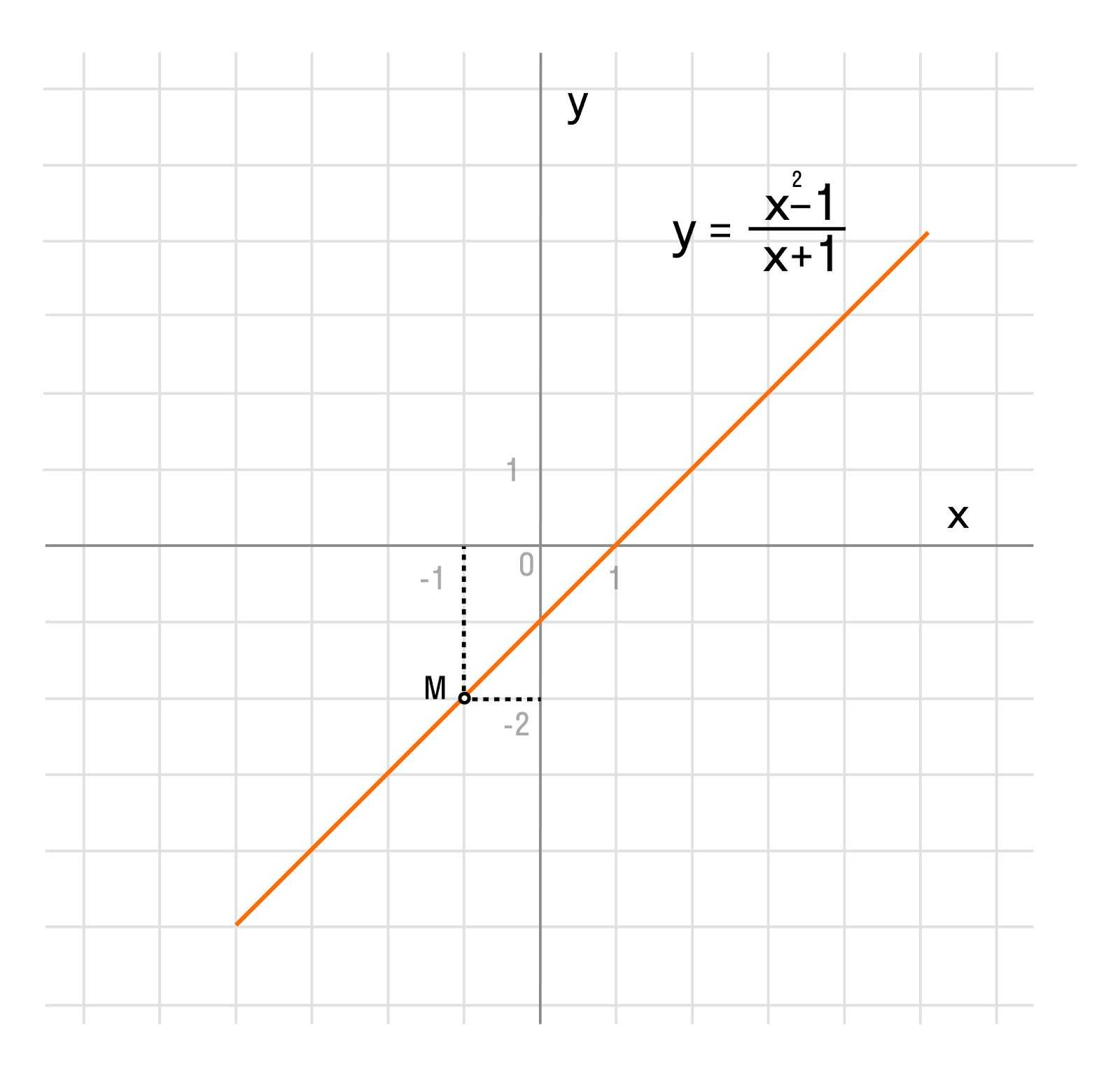
Упражнение 2. Построим график функции

Как мы решаем:

Выделим целую часть формулы функции:

График функции представляет собой гиперболу, сдвинутую на 3 вправо ix и 2 вверх iy и растянутую в 10 раз по сравнению с графиком функции

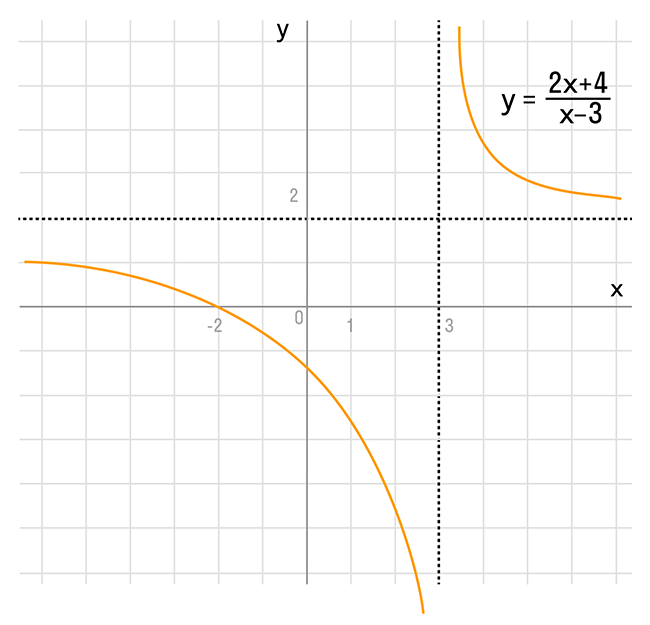
Упражнение 3. Построить графики функций:

а) у = 3х — 1

б) у = -х + 2

в) у = 2х

г) у = -1

Как мы решаем:

Воспользуемся методом построения линейных функций «по точкам».

а) у = 3х — 1

икс	у
-1
1	2

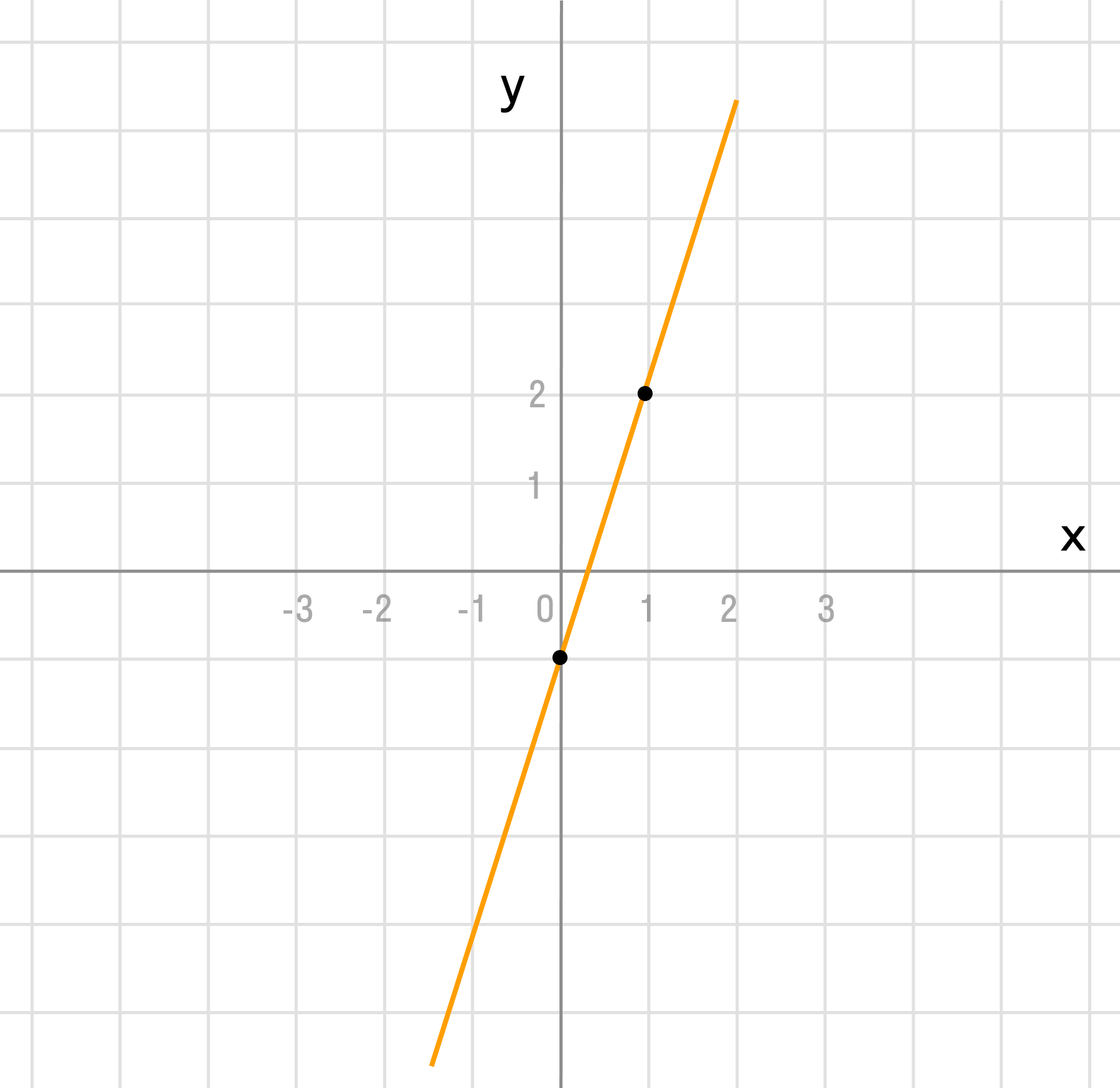
Как видно, k = 3 > 0 и угол наклона оси Ox острый, b = -1 — смещение по оси Oy.

б) у = -х + 2

икс	у
2
1	1

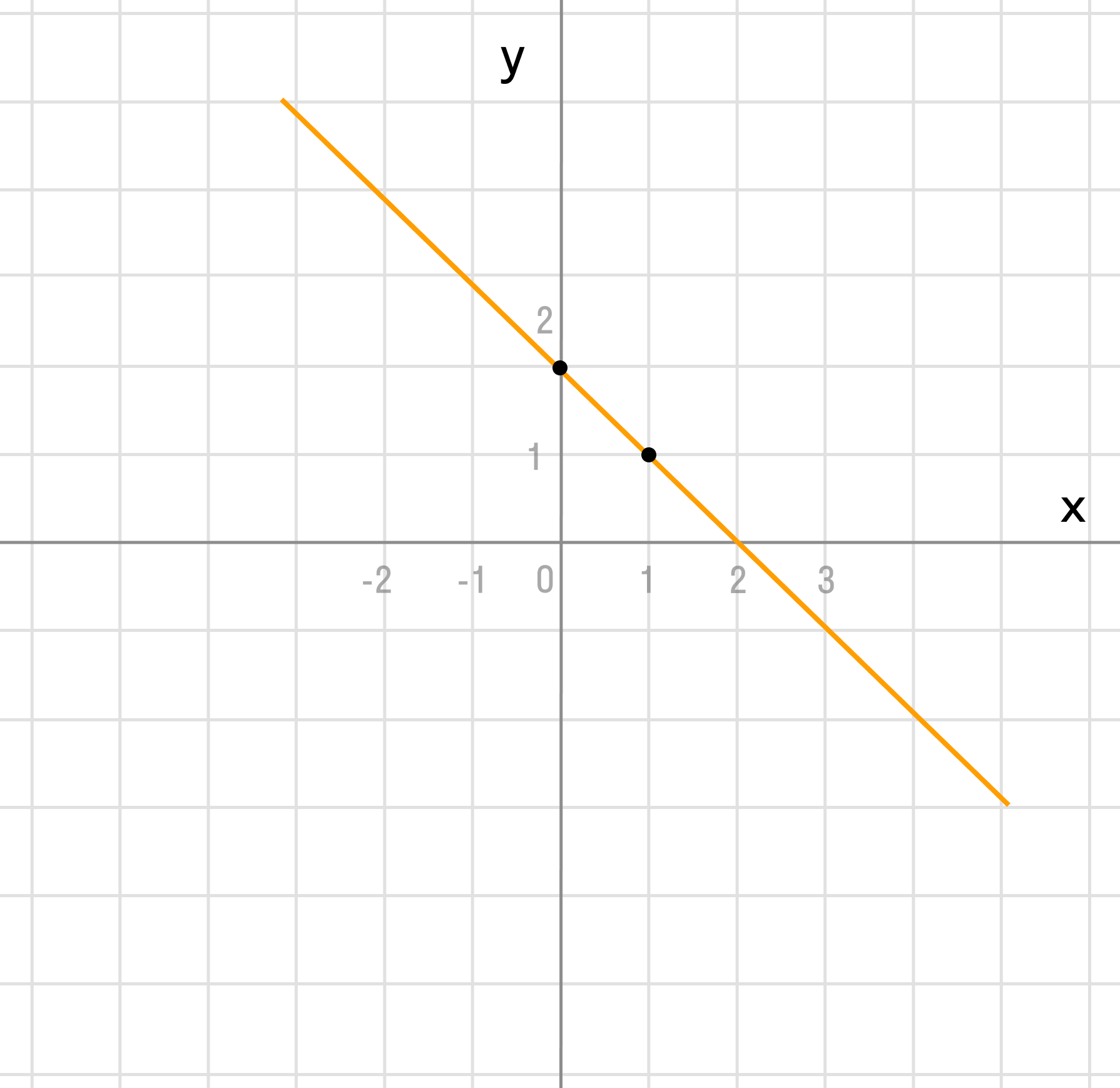
k = -1 > 0 и b = 2, мы можем сделать такие же выводы, как и в первом пункте.

в) у = 2х

икс	у
2

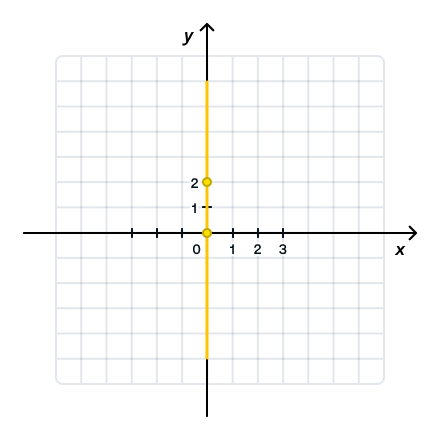
k = 2 > 0 — угол наклона оси Ox острый, b = 0 — график проходит через начало координат.

г) у = -1

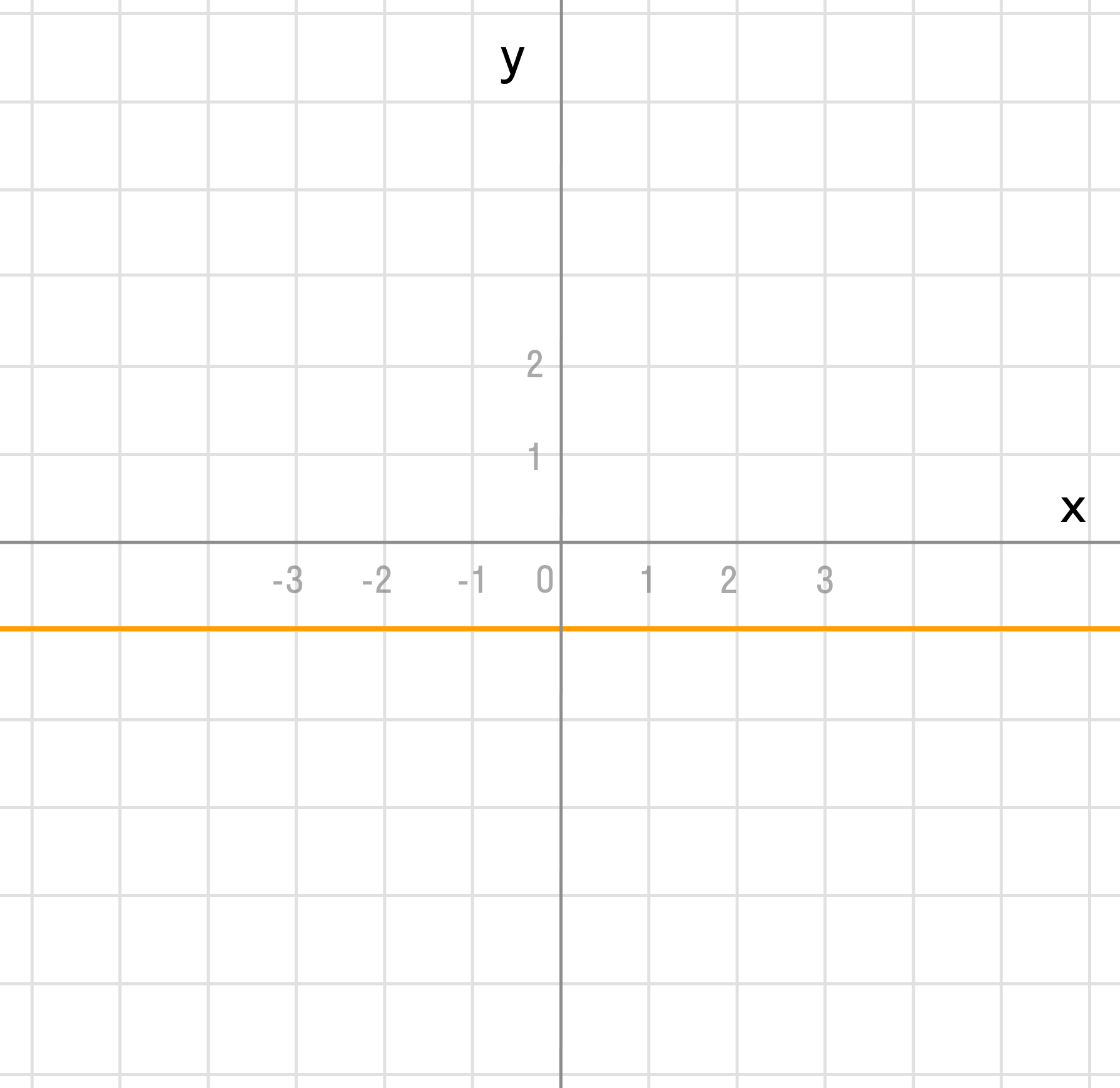
k = 0 — постоянная функция, прямая проходит через точку b = -1 и параллельна оси Ox.

Упражнение 4. Определите знаки коэффициентов общего вида функции y = ax2 + bx + c по виду графика.

Как мы решаем:

Вспомните, как параметры a, b и c определяют положение параболы.

1. Ветвится вниз, следовательно, a < 0.

   Точка пересечения с осью Oy c = 0.

   Координата вершины

2. Ветвится вверх, следовательно, a > 0.

   Точка пересечения с осью Oy c > 0.

   Координата вершины
   , так как неизвестное число при делении на положительное число дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

3. Ветвится вниз, следовательно, a < 0.

   Точка пересечения с осью Oy c > 0.

   Координата вершины
   , так как неизвестное число при делении на отрицательное дает положительный результат, то это число отрицательное, следовательно, b < 0.

Задача 5. Построить графики функций:

а) у = х² + 1

б)

в) у = (х — 1)² + 2

г)

д)

Как мы решаем:

Вы можете строить графики с помощью элементарных преобразований.

Если построить график функции y = f(x), то сдвигом графика f(x) будут получены следующие графики при a > 0).

• y = f(x) + a — график функции y = f(x) сдвигается вверх на a единиц;
• y = f(x) − a — график функции y = f(x) сдвинут вниз на единицу;
• y = f(x + a) — график функции y = f(x) смещен на одну единицу влево;
• y = f(x − a) — график функции y = f(x) сдвигается на единицу вправо.

Преобразуйте граф по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.

• Если m > 1, такое преобразование графа называется растяжением по оси y с коэффициентом m.

• Если m < 1, такое преобразование графика называется сжатием к оси x в 1/m раз.

один)

Преобразовать в одну операцию как f(x) + a.

у=х²

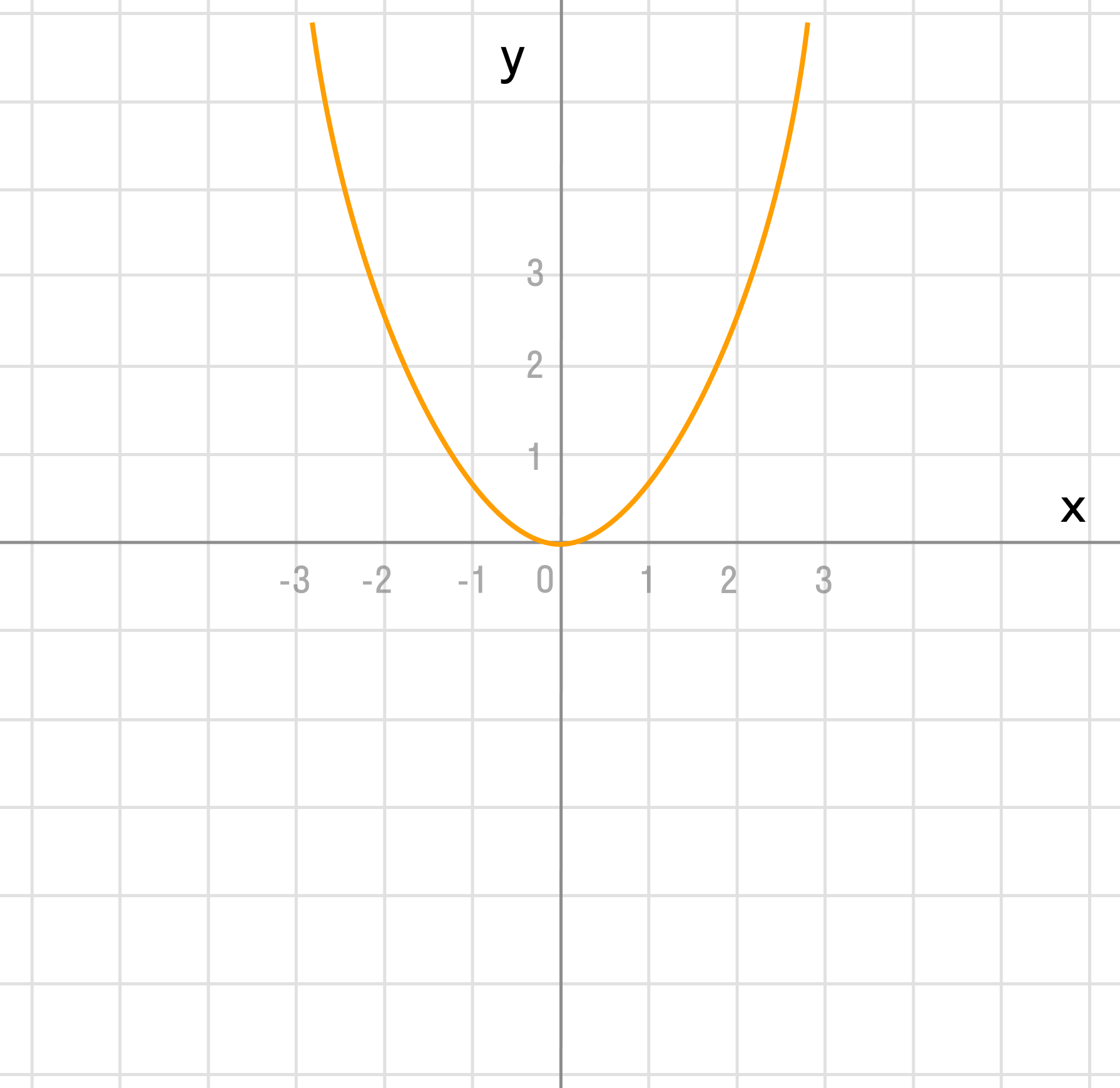
Переместить диаграмму вверх на 1:

у = х² + 1

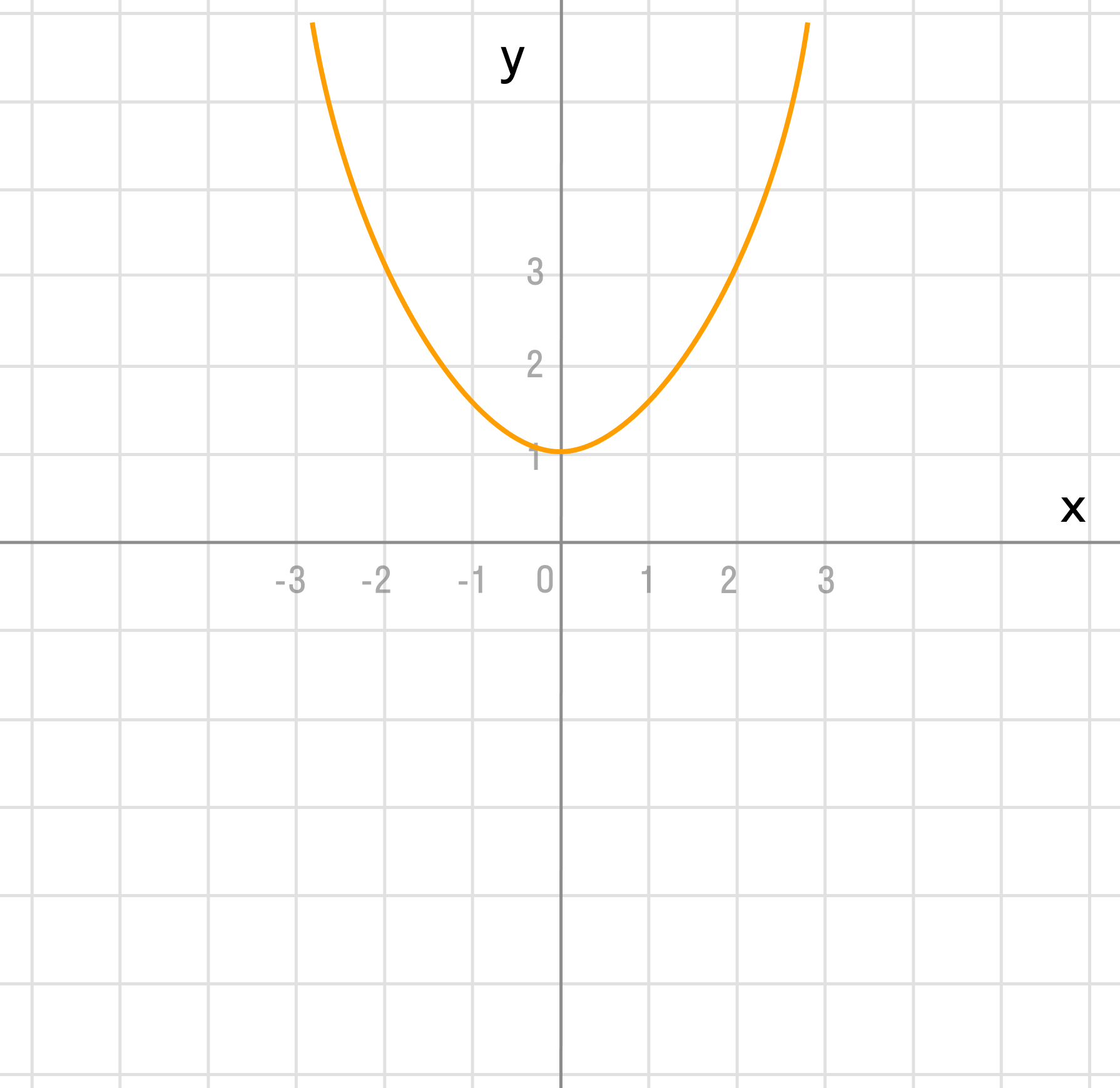
б)

Преобразовать в одну операцию как f(x — a).

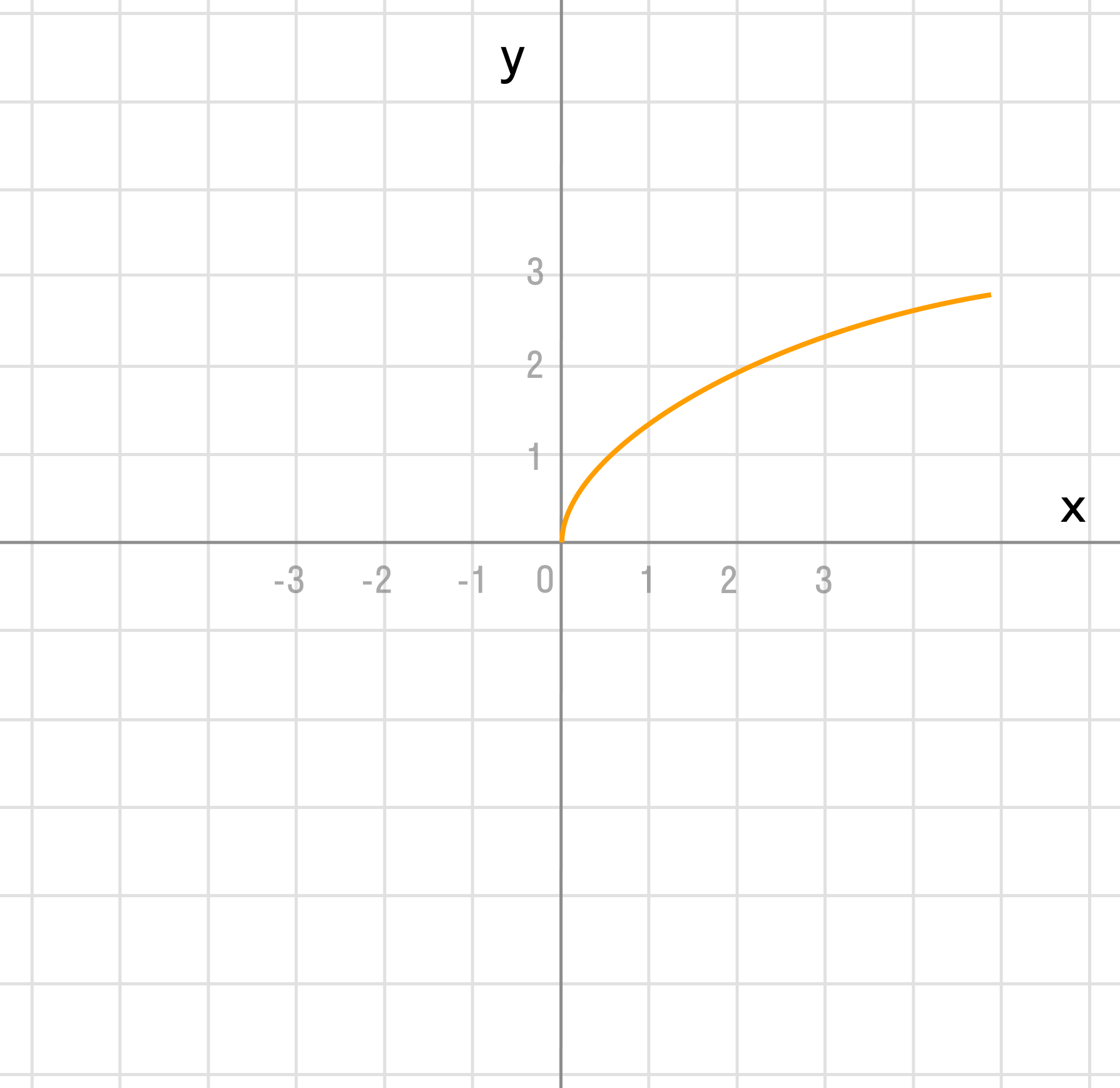
Сдвиньте диаграмму вправо на 1:

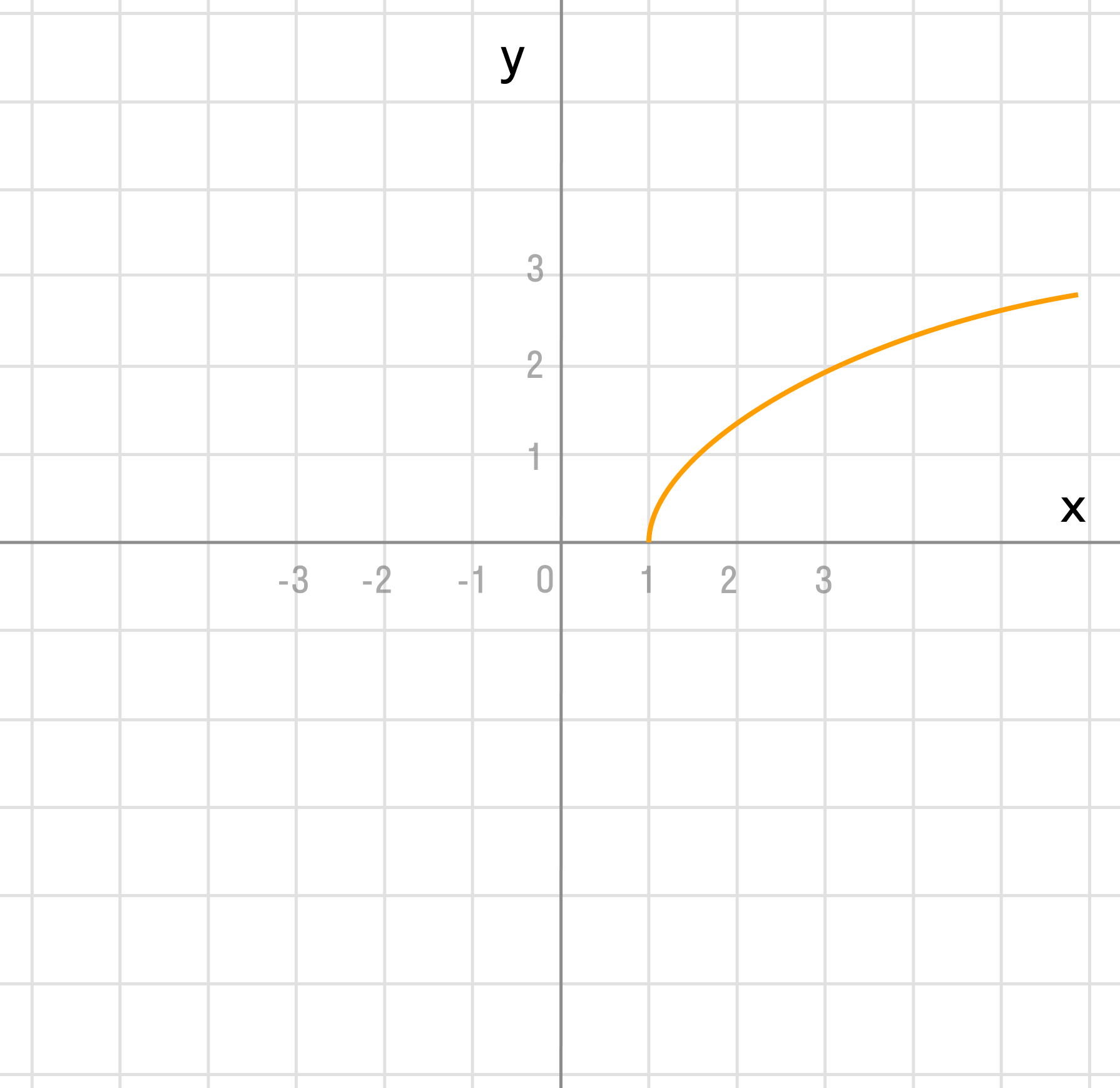
в) у = (х — 1)² + 2

В этом примере два преобразования, выполним их в порядке операций: сначала операции в скобках f(x — a), затем сложение f(x) + a.

у=х²

Сдвиньте диаграмму вправо на 1:

у = (х — 1)²

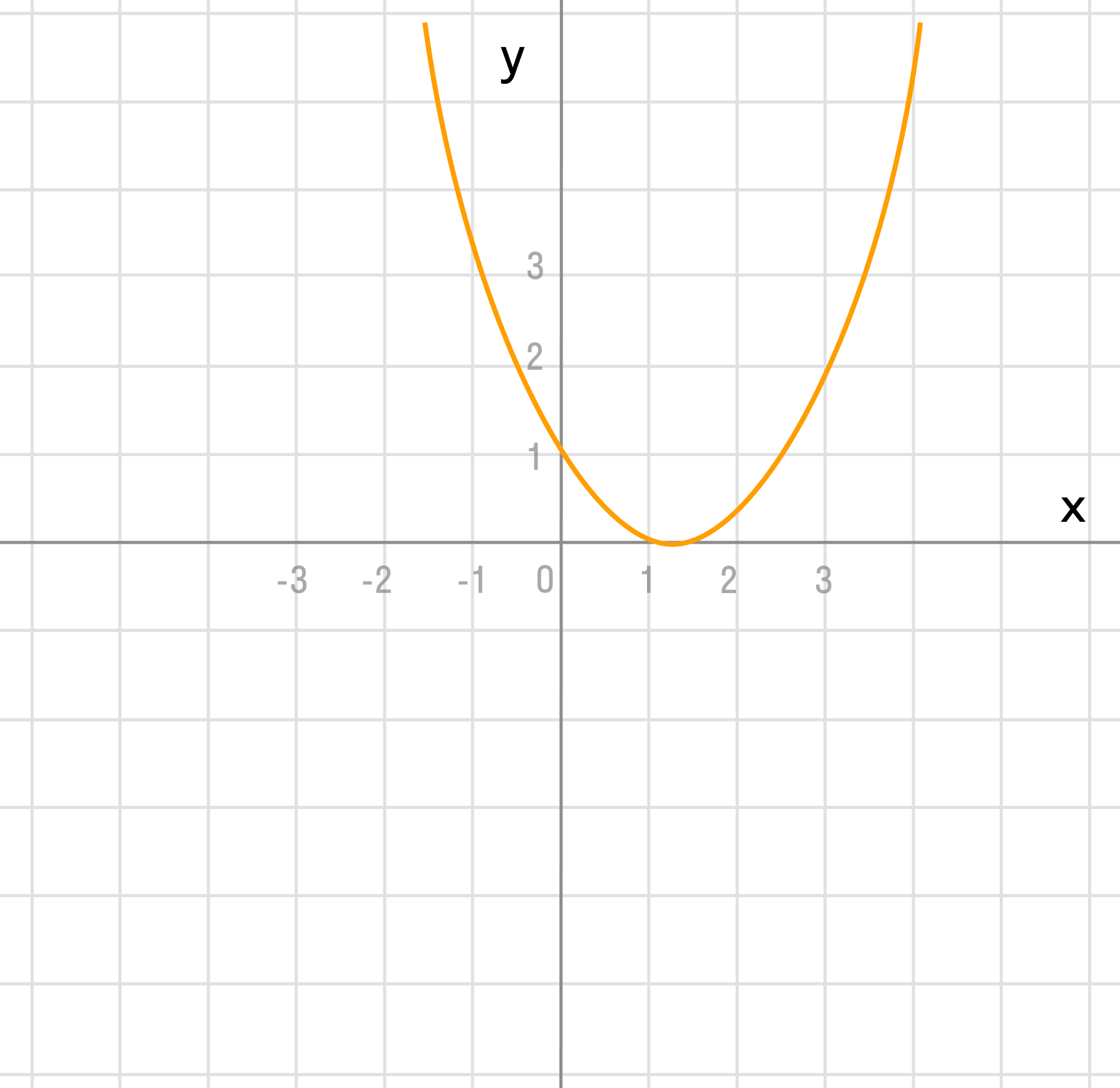
Переместите диаграмму вверх на 2:

у = (х — 1)² + 2

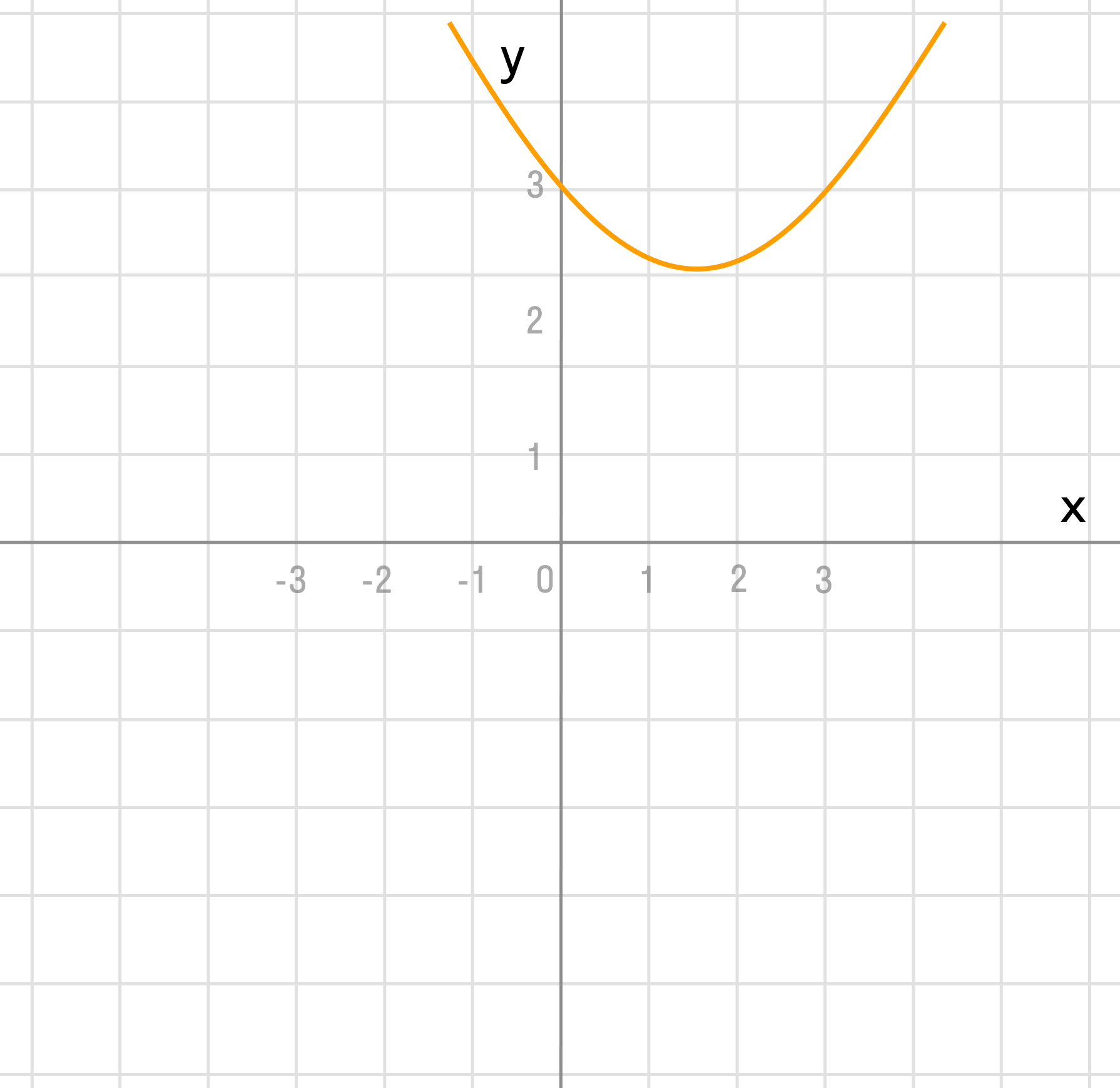
г)

Преобразование в один тип действия

у = потому что (х)

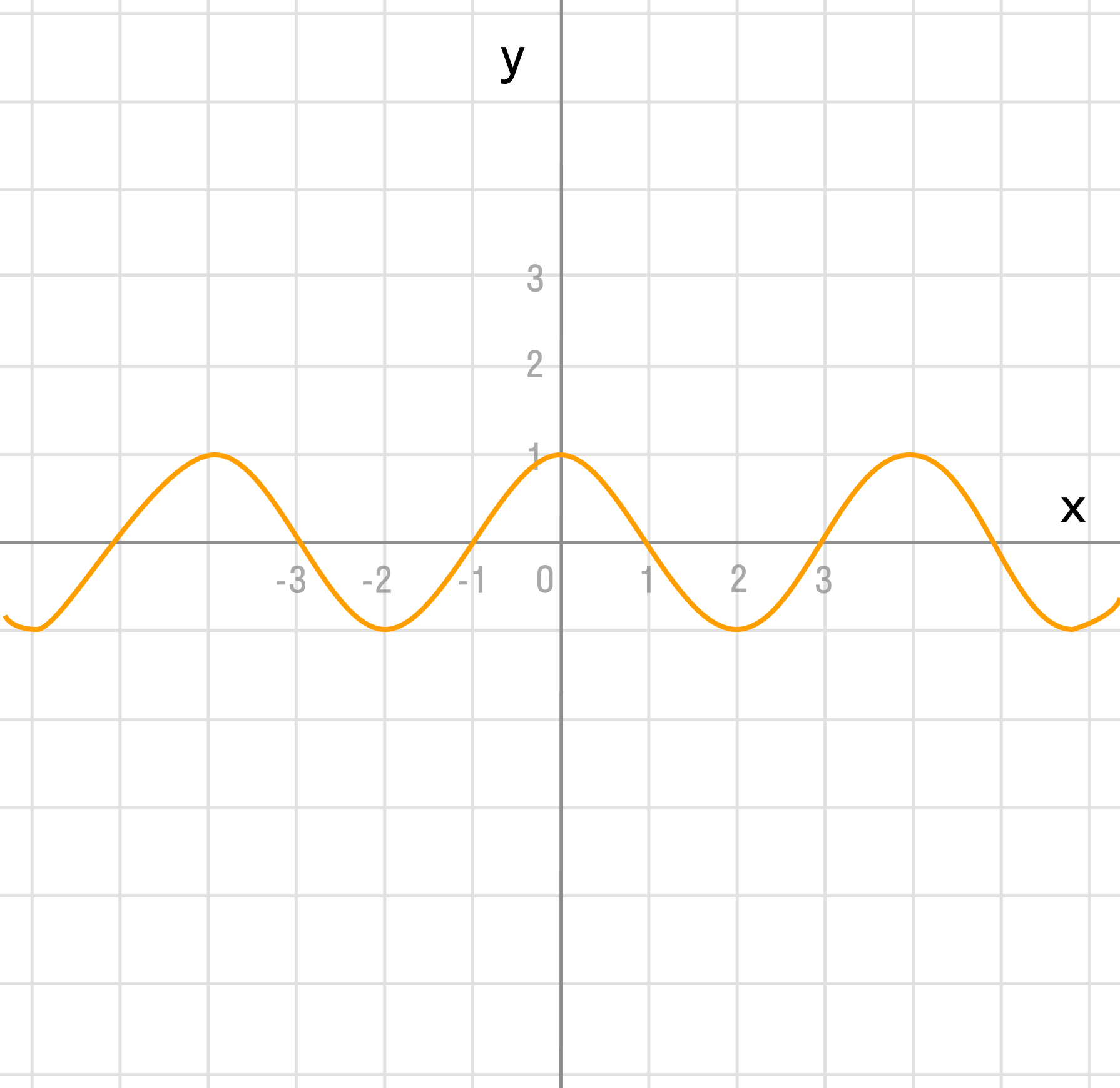
Продлим график 2 раза от оси ординат по оси абсцисс:

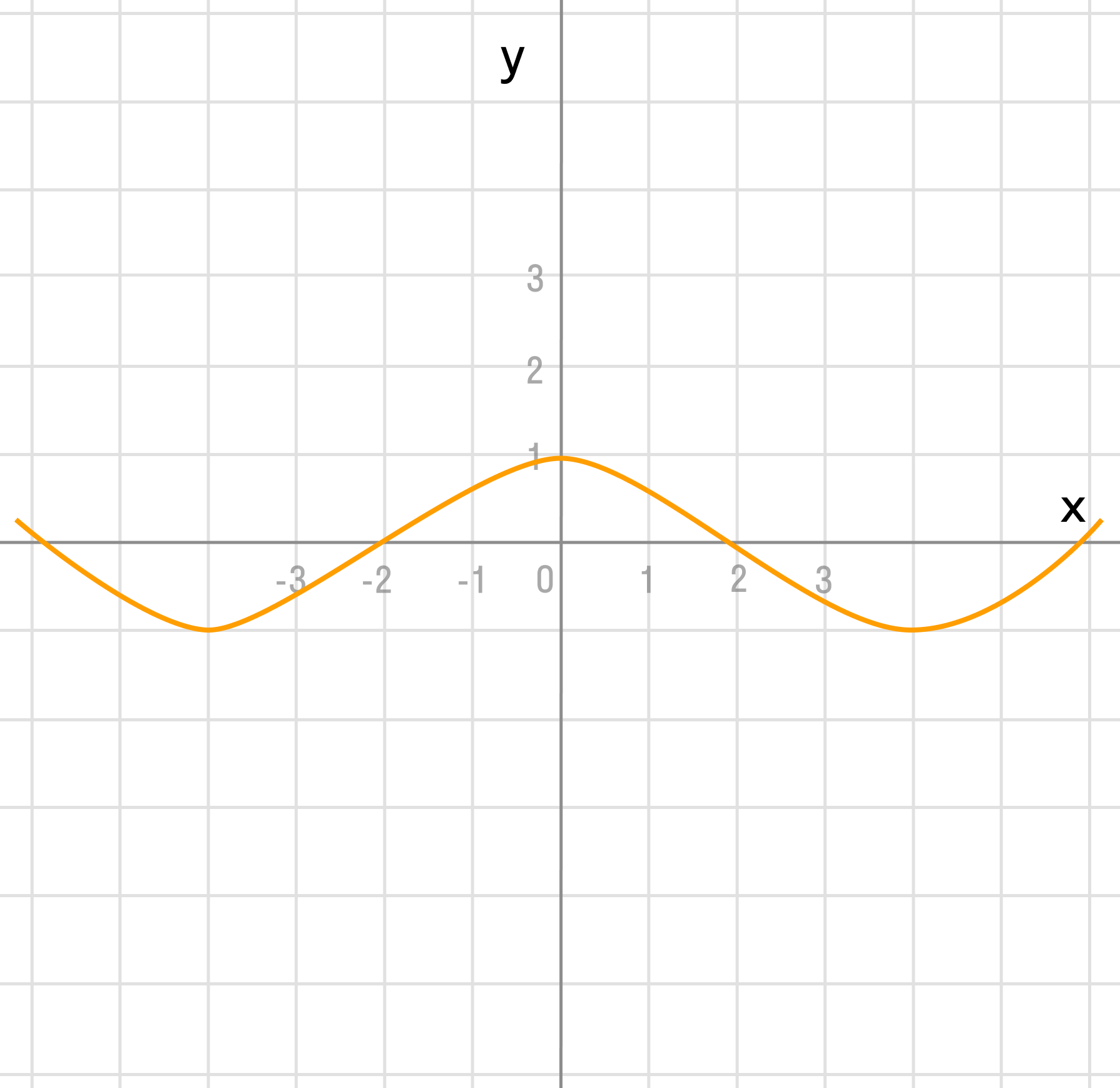
д)

Мы видим три преобразования вида f(ax), f(x + a), -f(x).

Для выполнения преобразований посмотрим на порядок действий: сначала умножаем, потом складываем и только потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, выносим двойку из скобок модуля.

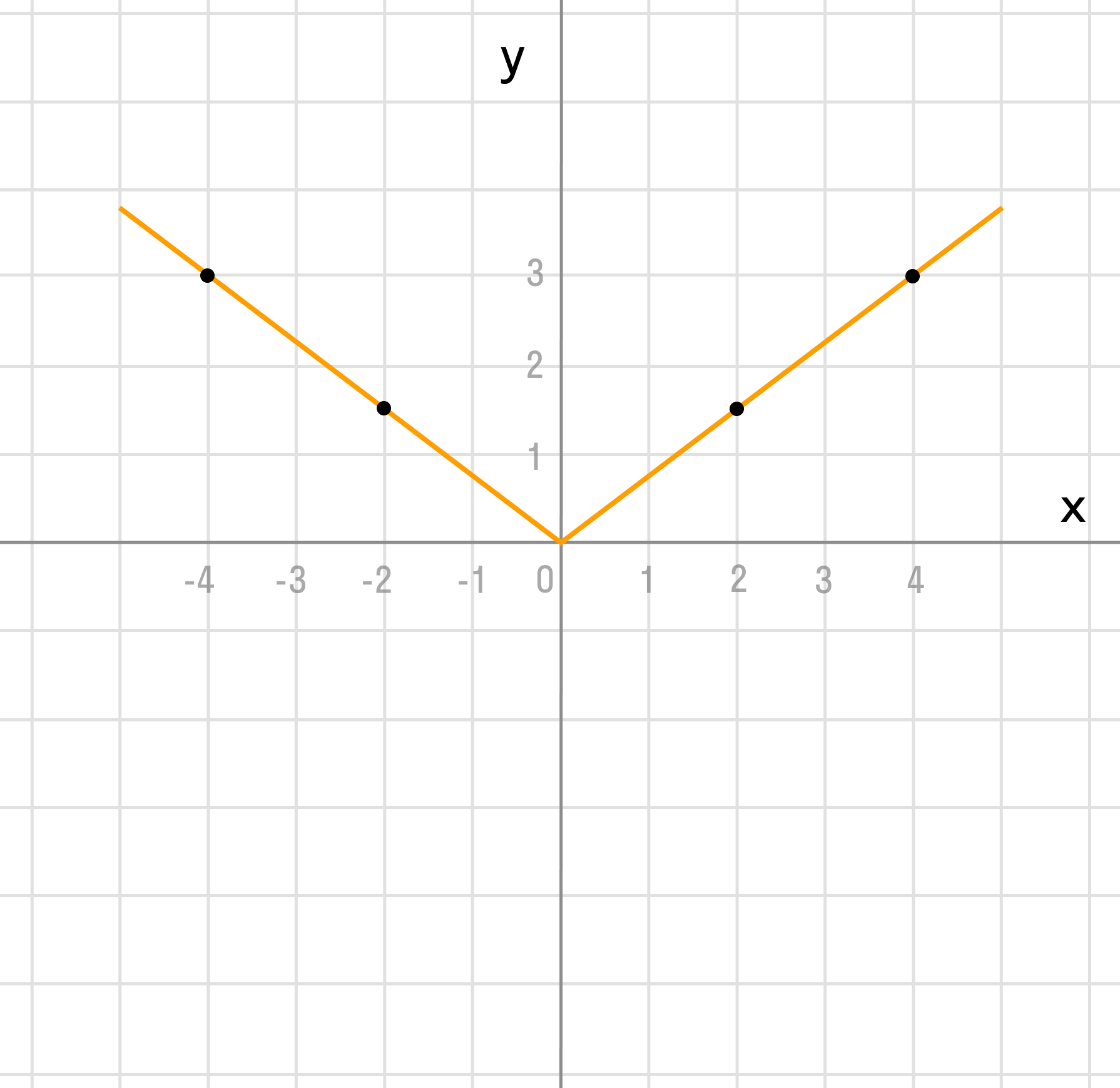
Сжимаем график дважды по оси x:

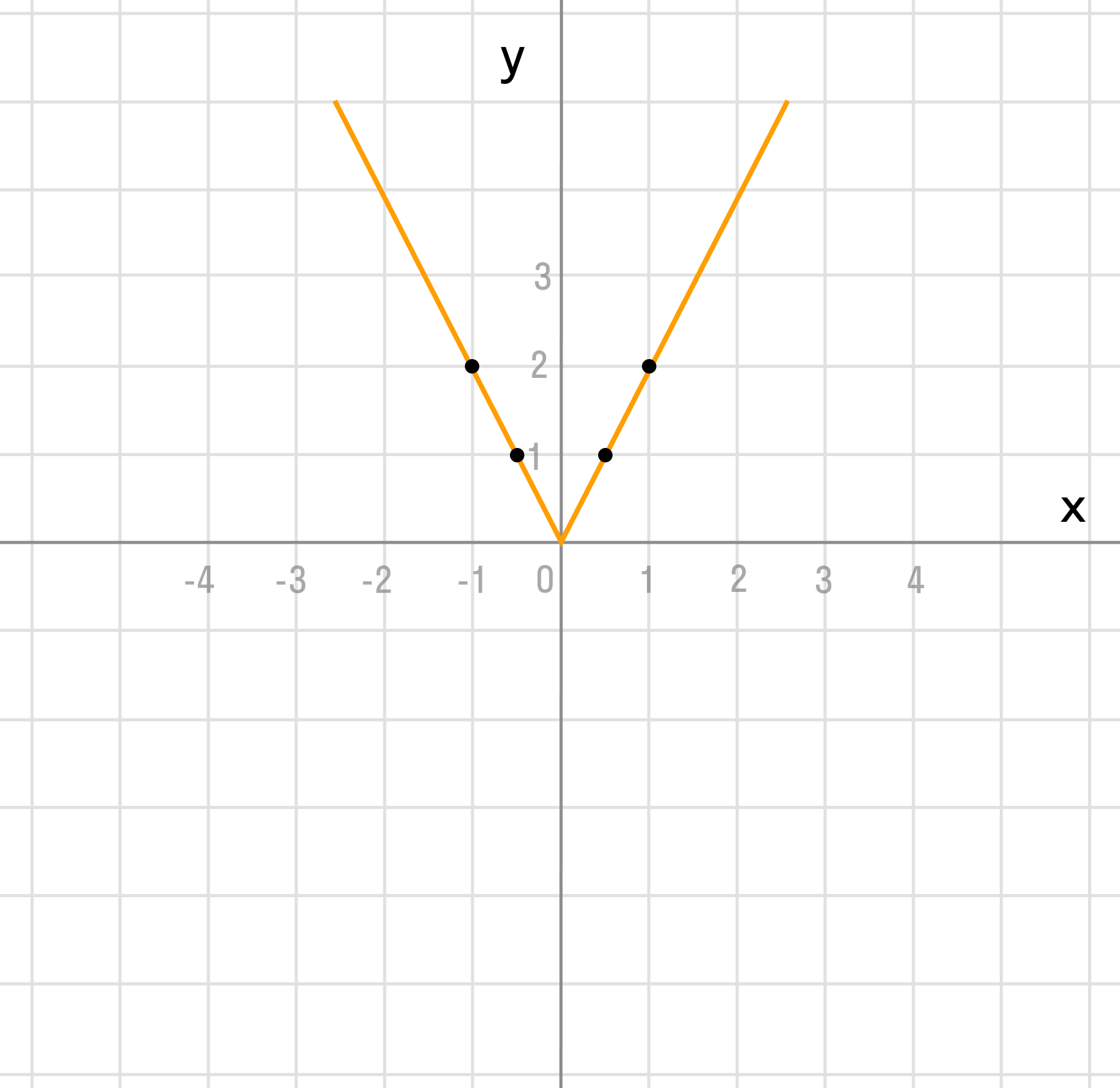
Сдвинем график влево на 1/2 по оси x:

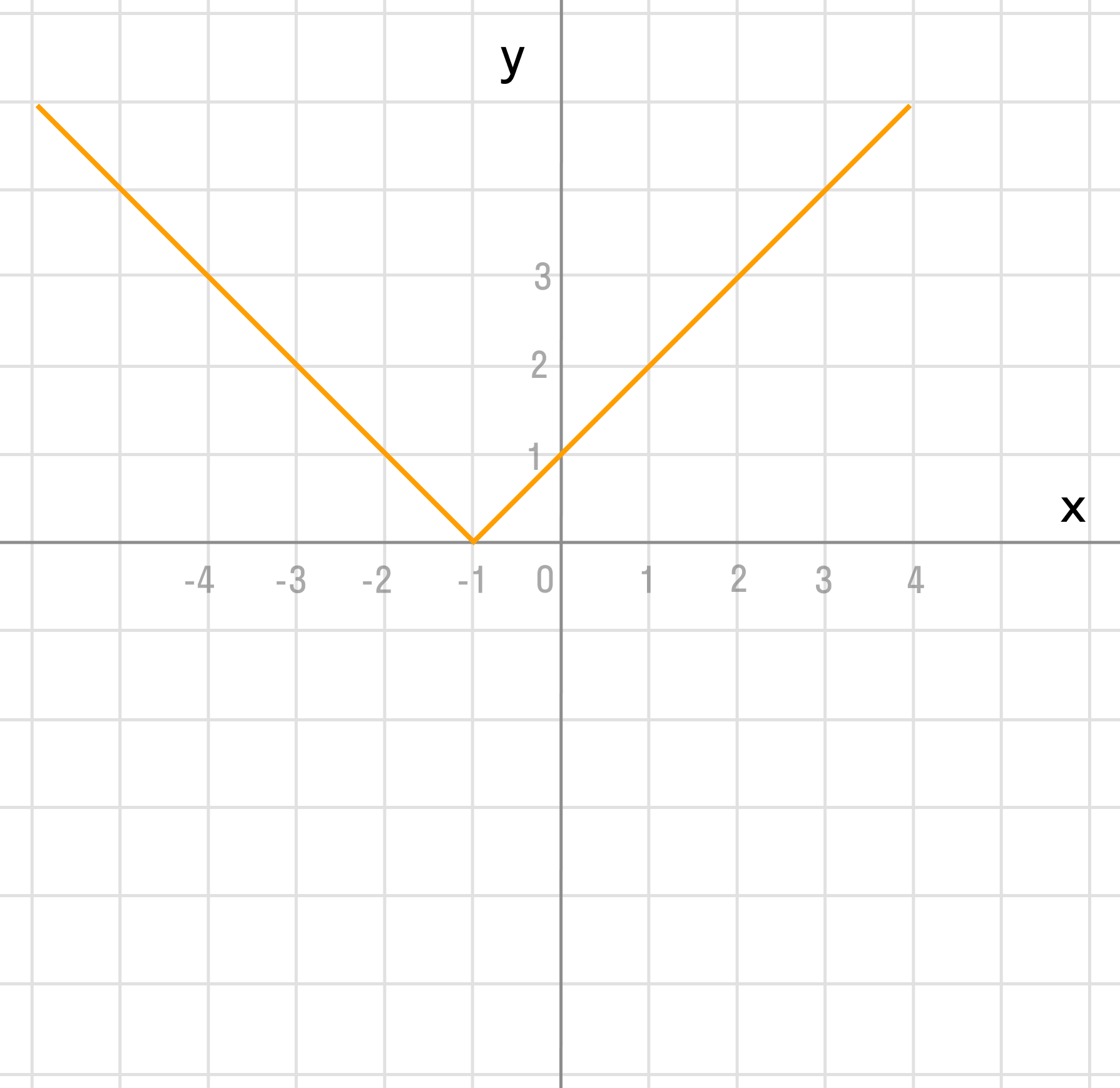
Отразим график симметрично относительно оси x:

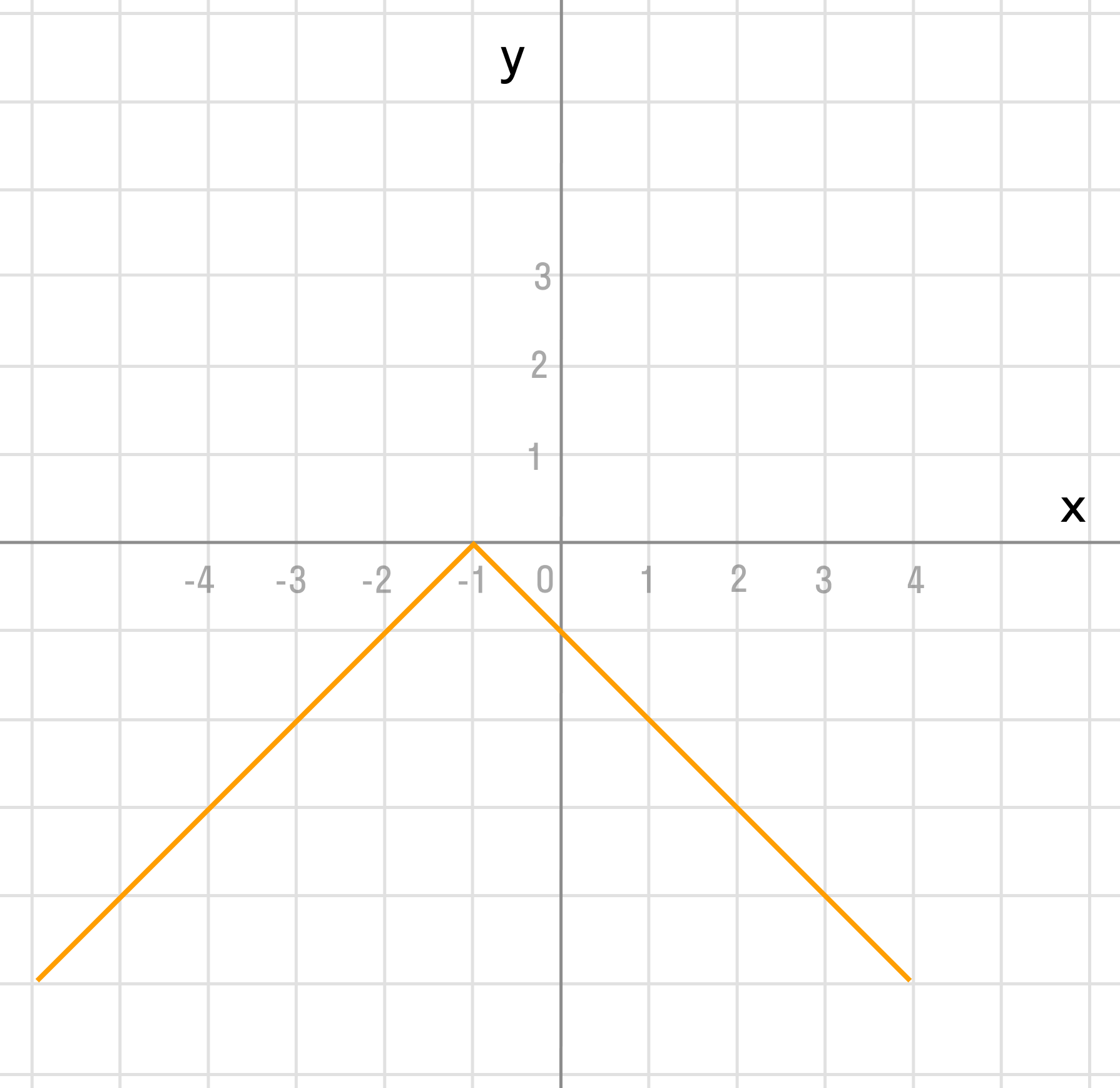
Примеры решения задач на нахождение формулы линейной функции по графику

Для того чтобы написать формулу линейной функции по графику, нужно знать координаты двух точек на этом графике. Рассмотрим пример. Допустим, на графике изображена прямая линия, проходящая через две точки: (-1, 3) и (4, -2). Наша задача — найти формулу этой линейной функции.

1. Шаг 1: Найдем коэффициент наклона (a) прямой, используя формулу a = (y2 — y1) / (x2 — x1). В нашем примере a = (-2 — 3) / (4 — (-1)) = -5 / 5 = -1.
2. Шаг 2: Зная коэффициент наклона a и одну из точек, например (-1, 3), можно найти свободный член (b) с помощью формулы b = y — ax. Подставим значения (-1, 3) и a = -1 в формулу и найдем b: b = 3 — (-1) * (-1) = 3 — 1 = 2.
3. Шаг 3: Полученные значения a = -1 и b = 2 позволяют нам написать формулу линейной функции: f(x) = -x + 2.

Таким образом, формула линейной функции по графику будет f(x) = -x + 2. Ее график будет представлять собой прямую линию, проходящую через точки (-1, 3) и (4, -2).

Еще один пример. Пусть график изображает прямую линию, проходящую через точки (0, 2) и (3, 5). Нам нужно найти формулу этой линейной функции.

1. Шаг 1: Найдем коэффициент наклона (a) применяя формулу a = (y2 — y1) / (x2 — x1). В нашем случае a = (5 — 2) / (3 — 0) = 3 / 3 = 1.
2. Шаг 2: Используя коэффициент наклона a и одну из точек, в данном случае (0, 2), найдем свободный член (b) по формуле b = y — ax. Подставим значения (0, 2) и a = 1, и найдем b: b = 2 — 1 * 0 = 2 — 0 = 2.
3. Шаг 3: Полученные значения a = 1 и b = 2 позволяют нам написать формулу линейной функции: f(x) = x + 2.

Таким образом, формула линейной функции по графику будет f(x) = x + 2. График этой функции — прямая линия, которая проходит через точки (0, 2) и (3, 5).

Пример 1

На рисунке изображен график линейной функции. Чтобы написать формулу этой функции, необходимо определить угловой коэффициент и свободный член.

Угловой коэффициент можно найти, определив отношение приращения функции к приращению аргумента. Для этого выберем две точки на графике и вычислим изменение функции и аргумента между ними. Затем, разделив изменение функции на изменение аргумента, получим угловой коэффициент.

Свободный член можно определить, зная значение функции в одной из точек на графике. Если на графике известна точка (x₁, y₁), то свободный член будет равен y₁ — угловой коэффициент * x₁.

Таким образом, формула линейной функции будет иметь вид y = kx + b, где k — угловой коэффициент, а b — свободный член.

Пример 2

На рисунке представлен график линейной функции. Чтобы написать формулу данной функции, нужно проанализировать его основные характеристики.

Линейная функция представляет собой прямую линию на графике, которая проходит через точку (0, b). На рисунке такая точка указана и ее координаты можно использовать для записи формулы.

Формула линейной функции имеет вид: y = kx + b, где k — коэффициент наклона прямой, а b — свободный член, показывающий точку пересечения с осью y.

Чтобы найти коэффициент наклона k, можно взять две точки на графике и использовать их координаты для нахождения разности по x и разности по y. Отношение разности по y к разности по x и будет равно коэффициенту наклона.

Таким образом, изучив график и пользуясь указанными формулами, можно сделать вывод о том, что формула линейной функции на рисунке будет выглядеть как y = kx + b, где k и b можно определить, проанализировав характеристики графика.

Рассмотрение случаев параллельных и совпадающих прямых

Рас­смот­рим при­мер:

При­мер 1:

, , 

По­стро­им гра­фи­ки дан­ных функ­ций. У каж­дой из них . У пер­вой , у вто­рой , у тре­тьей . На­пом­ним, что па­ра­мет­ры k и m опре­де­ля­ют­ся из стан­дарт­но­го вида ли­ней­но­го урав­не­ния , па­ра­метр  – это ор­ди­на­та точки пе­ре­се­че­ния пря­мой с осью у. Кроме того, от­ме­тим, что ко­эф­фи­ци­ент  от­ве­ча­ет за угол на­кло­на пря­мой к по­ло­жи­тель­но­му на­прав­ле­нию оси х, кроме того, если он по­ло­жи­тель­ный, то функ­ция будет воз­рас­тать, а если от­ри­ца­тель­ный – убы­вать. Ко­эф­фи­ци­ент  на­зы­ва­ет­ся уг­ло­вым ко­эф­фи­ци­ен­том.

Со­ста­вим таб­ли­цы для по­стро­е­ния гра­фи­ков:

х	-0,5
у	1

Таб­ли­ца для пер­вой функ­ции;

х	1
у	2

Таб­ли­ца для вто­рой функ­ции;

х	0,5
у	-1

Таб­ли­ца для тре­тьей функ­ции;

Оче­вид­но, что все по­стро­ен­ные пря­мые па­рал­лель­ны, по­то­му что их уг­ло­вые ко­эф­фи­ци­ен­ты оди­на­ко­вы. Функ­ции от­ли­ча­ют­ся толь­ко зна­че­ни­ем m.

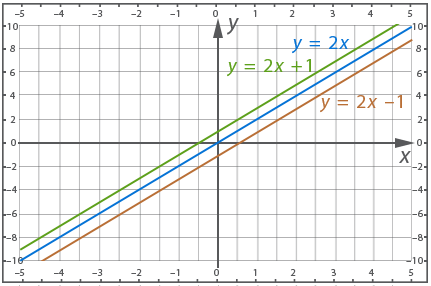
Рис. 1.

Сде­ла­ем вывод. Пусть за­да­ны две про­из­воль­ные ли­ней­ные функ­ции:

 и  

Если  но  то за­дан­ные пря­мые па­рал­лель­ны.

Если  и  то за­дан­ные пря­мые сов­па­да­ют.

Изу­че­ние вза­им­но­го рас­по­ло­же­ния гра­фи­ков ли­ней­ных функ­ций и свойств их па­ра­мет­ров яв­ля­ет­ся ос­но­вой для изу­че­ния си­стем ли­ней­ных урав­не­ний. Мы долж­ны за­пом­нить, что если пря­мые па­рал­лель­ны, то си­сте­ма не будет иметь ре­ше­ний, а если пря­мые сов­па­да­ют – то си­сте­ма будет иметь бес­чис­лен­ное мно­же­ство ре­ше­ний.

Свойства

• k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
• При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
• При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
• При k={\displaystyle k=0}, прямая параллельна оси абсцисс.

Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.

• b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
• При b={\displaystyle b=0}, прямая проходит через начало координат.

Понятие графика функции

График функции y = f(x) — это множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением этого графика.

График функции представляет собой набор точек (x; y), где x — аргумент, а y — значение функции, соответствующее данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив вместо функции xi все числа.

Например, возьмем простейшую функцию, где аргумент равен значению функции, то есть y = x.

В этом случае нам не нужно вычислять значение функции для каждого аргумента, так как они равны, поэтому абсцисса для всех точек графика будет равна ординате.

Отметьте на координатной плоскости любые три точки, например: L(-2;-2), M(0;0) и N(1;1).

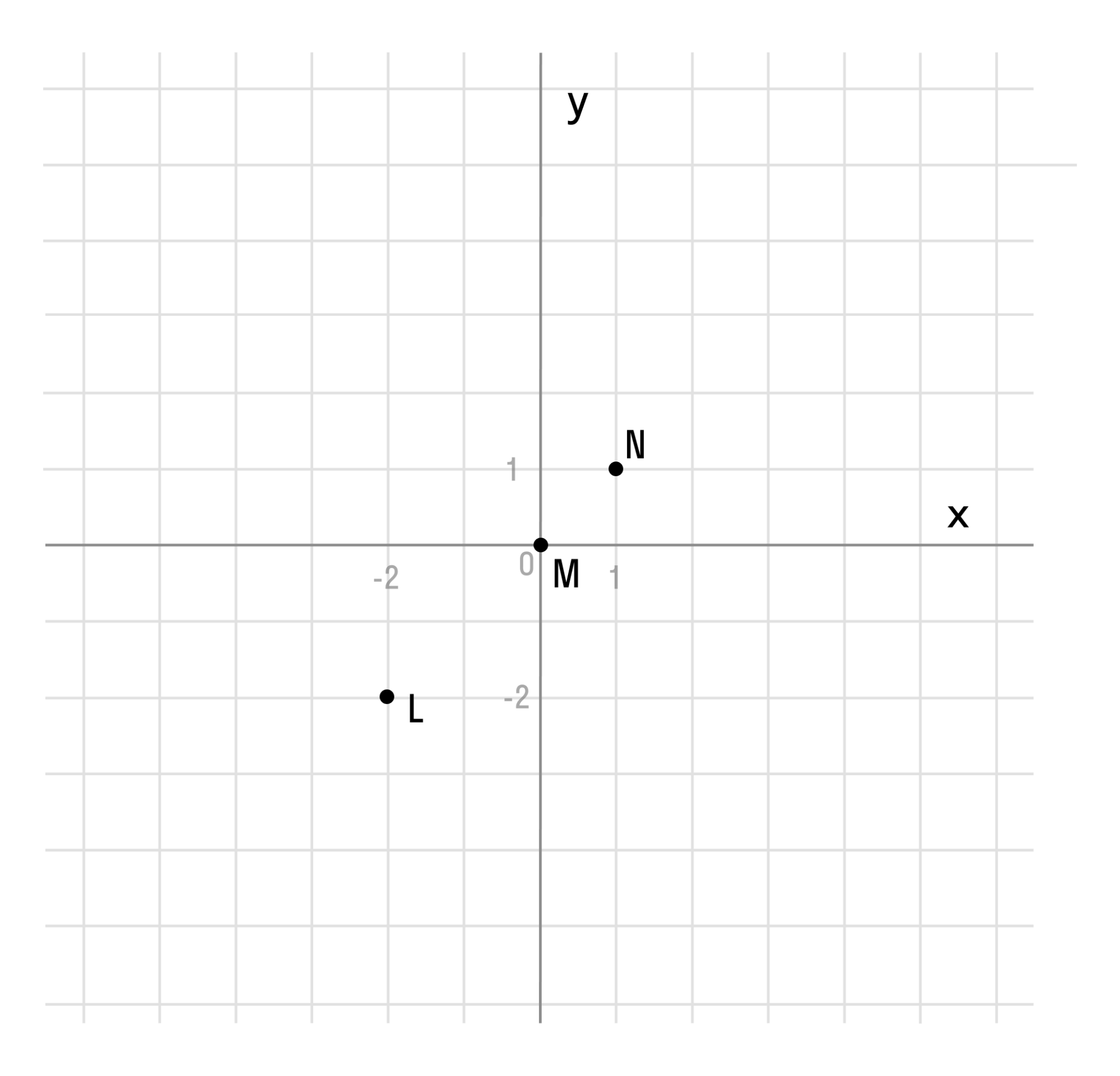
Если последовательно соединить отмеченные точки от наименьшего значения аргумента к наибольшему, то получится прямая линия. Таким образом, график функции y = x представляет собой прямую линию. На схеме это выглядит так:

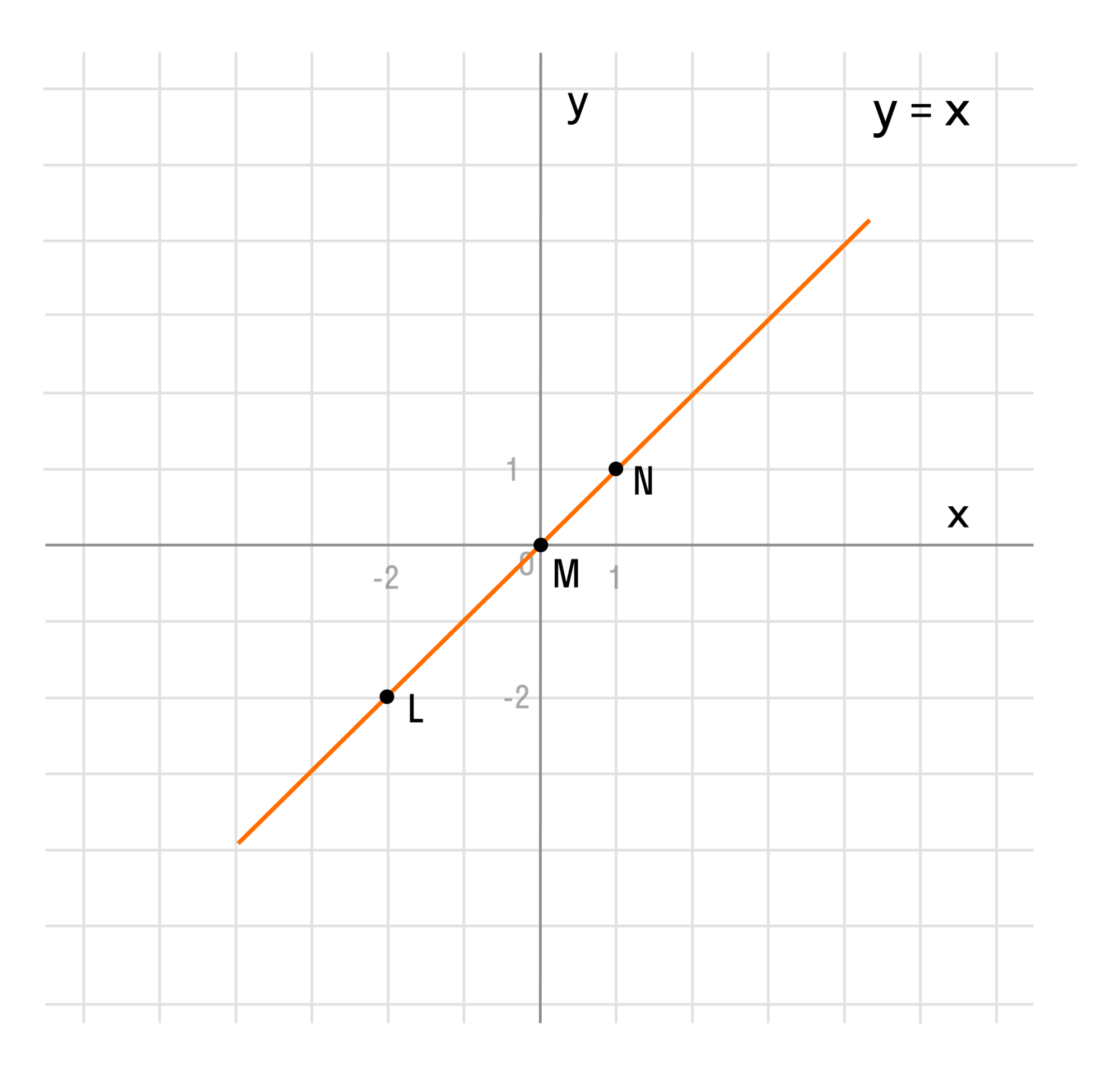
Надпись на чертеже у = х есть уравнение графика. Надпись с уравнением удобно нанести на чертеж, чтобы не запутаться при решении задач.

Важно отметить, что прямая бесконечна в обоих направлениях. Хотя мы и называем часть прямым графиком функции, на самом деле на чертеже показана лишь малая часть графика

Помнить! Не обязательно делать рисунок на весь тетрадный лист, вы можете выбрать удобный для вас масштаб, который будет отражать суть задачи.