Что такое предел функции

Предел функции.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Или другими словами, число A является пределом функции y = f (x) в точке x, если для всякой последовательности точек из области определения функции, не равных x, и которая сходится к точке x (lim x_n = x0), последовательность соответствующих значений функции сходится к числу A.

График функции, предел которой при аргументе, который стремится к бесконечности, равен L:

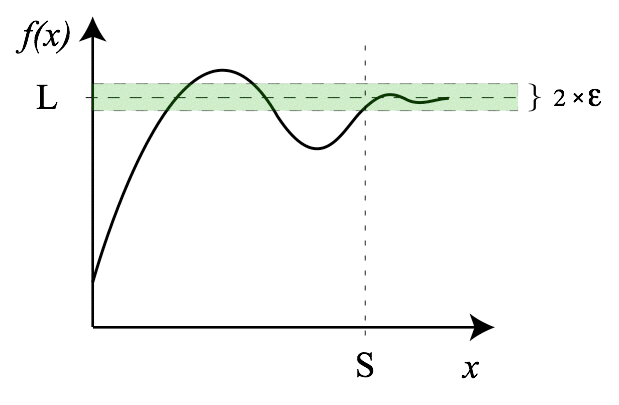
Предел функции по Гейне.

Значение А является пределом (предельным значением) функции f (x) в точке x в случае, если для всякой последовательности точек , которая сходится к x, но которая не содержит xкак один из своих элементов (т.е. в проколотой окрестности x), последовательность значений функции сходится к A.

Предел функции по Коши.

Значение A будет являться пределом функции f (x) в точке x в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x, удовлетворяющего условию 0 < | x – x0 | < δ, будет выполнено неравенство | f (x) A | < ε.

Найти предел функции.

Найти предел функции — будет очень просто, если вы понимаете суть предела и основные правила нахождения его. То, что предел функции f (x) при x стремящемся к a равен A, записывается таким образом:

Причем значение, к которому стремится переменная x, может быть не только числом, но и бесконечностью (∞), иногда +∞ или -∞, либо предела может вообще не быть.

Чтоб понять, как находить пределы функции, лучше всего посмотреть примеры решения.

Необходимо найти пределы функции f (x) = 1/x при:

Найдем решение первого предела. Для этого можно просто подставить вместо x число, к которому оно стремится, т.е. 2, получим:

Найдем второй предел функции. Здесь подставлять в чистом виде 0 вместо x нельзя, т.к. делить на 0 нельзя. Но мы можем брать значения, приближенные к нулю, к примеру, 0,01; 0,001; 0,0001; 0,00001 и так далее, причем значение функции f (x) будет увеличиваться: 100; 1000; 10000; 100000 и так далее. Т.о., можно понять, что при x → 0 значение функции, которая стоит под знаком предела, будет неограниченно возрастать, т.е. стремиться к бесконечности. А значит:

Касаемо третьего предела. Такая же ситуация, как и в прошлом случае, невозможно подставить ∞ в чистом виде. Нужно рассмотреть случай неограниченного возрастания x. Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю. Поэтому:

Ответ

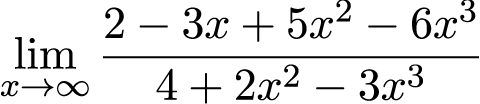
Необходимо вычислить предел функции

Приступая к решению второго примера, видим неопределенность . Отсюда находим старшую степень числителя и знаменателя – это x 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:

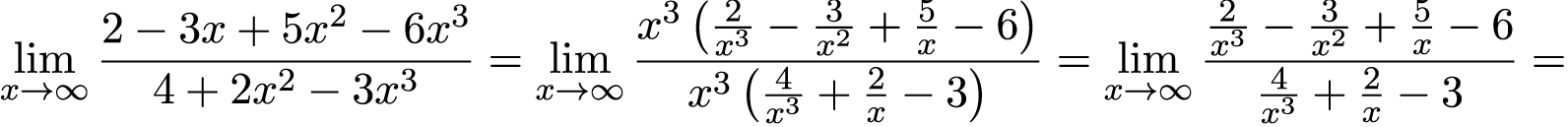
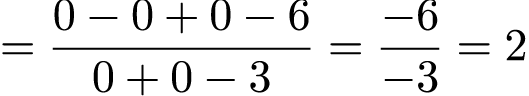
Ответ

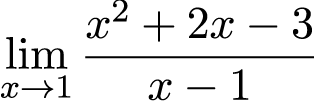
Необходимо рассчитать предел

Первым шагом в нахождении этого предела, подставим значение 1 вместо x, в результате чего имеем неопределенность . Для её решения разложим числитель на множители, сделаем это методом нахождения корней квадратного уравнения x 2 + 2x — 3:

Таким образом, числитель будет таким:

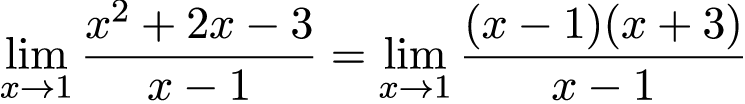
Далее сокращаем числитель и знаменатель на (x – 1):

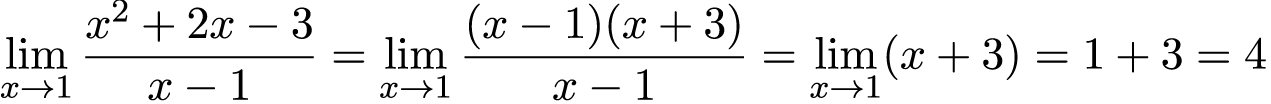
Ответ

Решение пределов функции.

Решение пределов функции — это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом.

Чтобы решить пределы, следуйте правилам:

1. Пробуем подставить в функцию число, результат решения и будет ответом.
2. Если х стремится не к числу, например в пределах вида или , то такие пределы решаются сразу, так как число, деленное на бесконечность, всегда дает 0, а деленное на нуль это и есть ∞. Если вам сложно понять саму суть бесконечности и нуля в пределах, то подставляйте вместо ∞ — бесконечно большое число – к примеру 1000 000, либо вместо нуля — бесконечно малое — например 0,000001 и после этого можете предположить к чему стремится ответ.
3. Существует группа пределов, в которых и в числитель, и в знаменатель при подстановке получаем либо нуль либо ∞. Это т.н. пределы с неопределенностью, часть из которых замечательные.

Разобравшись в сути и основных правилах решения предела, вы получите базовое понятие о том, как их решать.

Критерий Коши существования предела функции.

Будем говорить, что функция \(f(x)\) удовлетворяет в точке \(x=a\) условию Коши, если она определена в некоторой проколотой окрестности точки \(a\) и
$$
\forall\varepsilon>0\quad \exists\delta=\delta(\varepsilon)>0:\ \forall x’,x″\in \dot{U}_{\delta}(a)\rightarrow|f(x’)-f(x″)| < \varepsilon.\label{ref17}
$$

Лемма

Пусть существует число \(\delta >0\) такое, что функция \(f(x)\) определена в проколотой \(\delta\) — окрестности точки \(a\), и пусть для каждой последовательности {\(x_n\)}, удовлетворяющей условию \(x_n\in\dot{U}_{\delta}(a)\) при всех \(n\in\mathbb{N}\) и сходящейся к \(a\), соответствующая последовательность значений функции \({f(x_n)}\) имеет конечный предел. Тогда этот предел не зависит от выбора последовательности \({x_n}\), то есть если
$$
\lim_{n\rightarrow\infty}f(x_{n})=A,\nonumber
$$
и
$$
\lim_{n\rightarrow\infty}f(\widetilde{x_{n}})=\widetilde{A},\nonumber
$$
где \(\widetilde{x}_n =\dot{U}_{\delta}(a)\) при всех \(n \in\mathbb{N}\) и \( \widetilde{x}_{n}\rightarrow a \) при \(n\rightarrow\infty\) то \(\widetilde{A}=A.\)

\(\circ\) Образуем последовательность
$$
x_{1},\widetilde{x}_{1}, x_{2},\widetilde{x}_{2},\ldots, x_{n},\widetilde{x}_{n},\ldots\nonumber
$$
и обозначим k-й член этой последовательности через \(y_{k}\). Так как \(\displaystyle \lim_{k\rightarrow\infty}y_k=a\) (см. ) и \(y_k\in \dot{U}_{\delta}(a)\) при любом \(k\in\mathbb{N}\), то по условию леммы существует конечный \(\displaystyle \lim_{k\rightarrow\infty}f(y_{k})=A’\) Заметим, что \(\{f(x_{n})\}\) и \(\{f(\widetilde{x}_{n})\}\) являются подпоследовательностями сходящейся последовательности \(\{f(y_k)\}\). Поэтому \(A=A’,\widetilde{A}=A’\) откуда получаем, что \(A=\widetilde{A}.\ \bullet\)

Теорема 3

Для того чтобы существовал конечный предел функции \(f(x)\) в точке \(x = a\) необходимо и достаточно, чтобы эта функция удовлетворяла в точке a условию Коши \eqref{ref17}.

\(\circ\) Необходимость. Пусть \(\displaystyle \lim_{x\rightarrow a}f(x)=A\); тогда
$$
\forall\varepsilon>0 \ \exists\delta>0:\forall x\in\dot{U}_{\delta}(a)\rightarrow|f(x)-A|<\frac{\varepsilon}{2}.\label{ref18}
$$

Если \(х’,x″\) любые точки из множества \(\dot{U}_{\delta}(a)\), то из \eqref{ref18} следует, что
$$
|f(x’)-f(x″)|=|(f(x’)-A)-(f(x″)-A)|\leq|f(x’)-A|+|f(x″)-A| <\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon,\nonumber
$$
то есть выполняется условие Коши \eqref{ref17}.

Достаточность. Докажем, что если \(\exists\delta_{0}:\dot{U}_{\delta}(a)\subset D(f)\) и выполняется условие \eqref{ref17}, то существует предел функции \(f\) в точке \(a\). Воспользуемся определением предела функции по Гейне. Пусть \(\{x_{n}\}\) — произвольная последовательность такая, что \(x_n\in\dot{U}_{\delta}(a)\) и \(\displaystyle\lim_{x\rightarrow\infty}x_n=a.\) Докажем, что соответствующая последовательность значений функции \(\{f(x_{n})\}\) имеет конечный предел, не зависящий от выбора последовательности \(\{x_{n}\}\)

Если выполняется условие \eqref{ref17}, то для каждого \(\varepsilon>0\) можно найти число \(\delta=\delta_\varepsilon>0\) такое, что
$$
\forall x’,x″\in \dot{U}_{\delta}(a)\rightarrow|f(x’)-f(x″)| <\varepsilon.\label{ref19}
$$

Так как \(\displaystyle \lim_{x\rightarrow\infty}x_{n}=a\), то, задав число \(\delta=\delta(\varepsilon)>0,\) указанное в условии \eqref{ref19}, найдем в силу определения предела последовательности номер \(n_{\delta}=N_{\varepsilon}\) такой, что
$$
\forall n>N_{\varepsilon}\rightarrow 0<|x_{n}-a| <\delta.\nonumber
$$
Это означает, что для любого \(n\geq N_{\varepsilon}\) и для любого \(m\geq N_{\varepsilon}\) выполняются условия \(x_{n}\in \dot{U}_{\delta}(a),\ x_{m}\in \dot{U}_{\delta}(a)\) и в силу \eqref{ref19} \(|f(x_n)-f(x_m)| <\varepsilon\). Таким образом, последовательность \(\{f(x_{n})\}\) является фундаментальной и согласно критерию Коши для последовательности имеет конечный предел. В силу леммы этот предел не зависит от выбора последовательности \(\{x_{n}\}\) сходящейся к точке \(a\). Следовательно, функция \(f(x)\) имеет конечный предел в точке \(a\). \(\bullet\)

Замечание.

остается в силе, если точку \(a\) заменить одним из символов \(a-0, a+0,-\infty, +\infty\); при этом условие \eqref{ref17} должно выполняться в окрестности этого символа.

Свойства величин последовательностей

Казалось бы, предел числовой последовательности уже разобран довольно подробно, однако не раз упоминаются такие фразы, как «бесконечно маленькие» и «бесконечно большие» числа. Очевидно, если есть последовательность 1/х, где x→∞, то такая дробь бесконечно малая, а если та же последовательность, но предел стремится к нулю (х→0), то дробь становится бесконечно большой величиной. А у таких величин есть свои особенности. Свойства предела последовательности, имеющей какие угодно малые или большие величины, состоят в следующем:

1. Сумма любого количества сколько угодно малых величин будет также малой величиной.
2. Сумма любого количества больших величин будет бесконечно большой величиной.
3. Произведение сколь угодно малых величин бесконечно мало.
4. Произведение сколько угодно больших чисел — величина бесконечно большая.
5. Если исходная последовательность стремится к бесконечно большому числу, то величина, ей обратная, будет бесконечно малой и стремиться к нулю.

На самом деле вычислить предел последовательности — не такая сложная задача, если знать простой алгоритм. Но пределы последовательностей — тема, требующая максимума внимания и усидчивости. Конечно, достаточно просто уловить суть решения подобных выражений. Начиная с малого, со временем можно достигнуть больших вершин.

Сегодня на уроке мы разберём строгое определение последовательности
и строгое определение предела функции
, а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна
. И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!)
о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)

– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ноги руку помощи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций
, в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей
, на котором я фактически уже сформулировал строгое определение.

Какие значки помимо знаков неравенств и модуля вы знаете?

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что»
, в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;

– для всех «эн», бОльших чем ;

– знак модуля означает расстояние
, т.е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

Предел и его обозначение

Предел функции как один из важнейших разделов математического анализа определяет предельное значение функции, т.е. такое значение, после достижения которого функция уже не существует.

Разберем обозначение «предела»:

1. Знак предела lim;

2. $x\to a$ — это стремление х к определенной точке или бесконечности

   ($x\to \infty $)

3. $f(x)=b$ — функция

Среди данных обозначений х является числовой переменной, которая изменяется на области Х (координатной плоскости оХ и оY). Рассмотрим график простейшей функции на рис.1. Оси графика образуют область ее изменения и говорят, что функция $y=x^{2} $ определена на множестве Х. Кроме числовой независимой переменной х, каждая функция имеет зависимую от х переменную y (иначе говоря, частное решение в конкретной точке).

Совокупность всех значений зависимой переменной составляет множество значений функции. На графике множество значений можно определить по оси оY, а область определений по оХ. Для рассматриваемого графика, область значений определяется как , а область определений .

«Стремление» х означает последовательное приближение к числу а (предельной точки области Х или бесконечности) путем перебора максимально близких к нему значений.

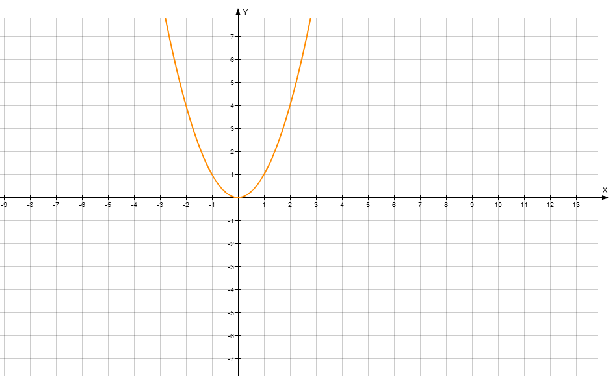
Рисунок 1. Функция $x^{2} $

Рассмотрим следующее выражение:

Его «чтение» должно производиться следующим образом: «Предел функции х + 4 при стремлении х к бесконечности»

Определение

Пределом является число b, к которому стремится функция, при стремлении x к а.

Проще говоря, к какому числу приблизится функция, при стремлении ее неизвестной к а.

Непрерывная функция

Функцию, которая имеет предел в точке a, называют непрерывной в этой точке.

\

Рассмотрим условия непрерывности функции:

1. Функция должна быть определена, т.е. существует f(a);
2. Предел функции в точке а — существует;
3. Предел функции в точке х = а равен значению функции в этой точке

Если функция y = f(x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.

Теоремы непрерывности функции

Теорема 1

Если функции f(x) и g(x) непрерывны в точке х = а, то в этой точке непрерывны и такие функции, как:

• f(x) + g(x),
• f(x) — g(x),
• f(x) • g(x).

Теорема 2

Если функции f(x) и g(x) непрерывны в точке х = а и g(а) ≠ 0, то в точке х = а будет непрерывной также и функция f(x)/g(x).

Непрерывными являются функции вида:

• Многочлены

  \

• Дробно-рациональные функции (кроме нулей знаменателя)

  \

• Тригонометрические функции

$у = sin(x), y = cos(x), y = tg(x), y = ctg(x)$

$у = arcsin(x), y = arccos(x), y = arctg(x), y = arcctg(x)$

Показательные и логарифмические функции, а также модуль

\{x} y=\left|x\right|\]

Примеры непрерывных функций:

1. $y=x^{2} +4x-5$
2. $y=\frac{x^{2} -2}{x-3} $ (кроме точки 3)
3. $y=\sqrt{x} $

Пример 1

Является ли сумма непрерывной, если обе функции непрерывны в точке в точке х = а?

\

Ответ: по теореме 1 функция непрерывна

Проверка функций на неопределенность проводится методом подстановки а вместо х, НО полученное значение предела у НЕПРЕРЫВНОЙ функции всегда равно числу а.

Пример 2

Является ли функция непрерывной?

\

Решение:

\

$1 = 1$

Вывод: функция непрерывна в точке 1

Что такое предел в математике

Когда математики говорят о пределах, то имеют в виду такую последовательность событий:

1. Есть функция — это просто какая-то «коробка» с математикой. Ты ей на вход число, она его обрабатывает у себя внутри и отдаёт другое число.
2. У функции есть как минимум два числа: то, которое ты ей даёшь на вход; и то, которое получаешь на выходе.
3. Иногда математикам интересно, что будет, если число на входе будет к чему-то стремиться. А именно: «Если число на входе будет стремиться вот сюда, куда будет стремиться число на выходе?»

Стремиться — значит стараться приблизиться к какому-то числу, но не достигнуть его.

Если мы говорим, что переменная функции стремится к бесконечности, то это значит, что с каждым новым вычислением мы берём значение переменной больше предыдущего.

1, 2, 3, … 1000000000000003, 1000000000000004 и так до бесконечности

Наоборот тоже работает: если переменная функции стремится к нулю, то это значит, что она постоянно уменьшается:

1, 0.1, 0.01, 0.001, … 0.00000000000000000000000001 и с каждым разом число будет ближе к нулю, но никогда его не достигнет.

Стремление переменной к числу обозначается стрелкой: x→0, а предел — словом lim:

Предел функции по Гейне

Значение А является пределом (предельным значением) функцииf (x) в точке  x0 в случае, если для всякой последовательности точек
, которая сходится к  x0, но которая не содержит  x0как один из своих элементов (т.е. в проколотой окрестности  x0), последовательность значений функции
сходится к A.

Предел функции по Коши

Значение A будет являться пределом функцииf (x) в точке  x0 в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x, удовлетворяющего условию 0 < | x – x0 | < δ, будет выполнено неравенство | f (x) A | < ε.

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

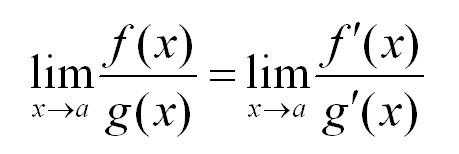
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

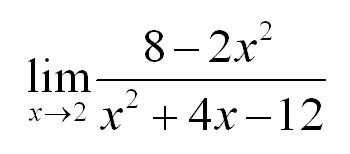
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

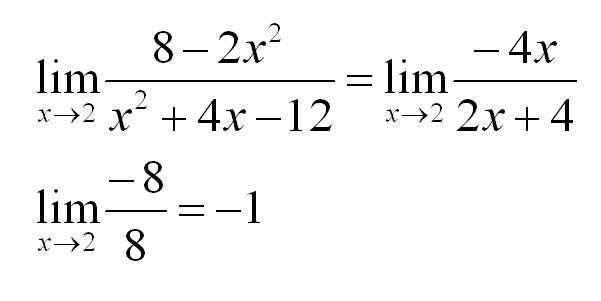
Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Результат

Примеры пределов

• Пределы от рациональных дробей на бесконечности
• Пределы от рациональных дробей в конечной точке
• Пределы от дроби в нуле
• Первый замечательный предел
• Второй замечательный предел
• Пределы с квадратными корнями
• Правило Лопиталя

Указанные выше примеры содержат также:

• квадратные корни sqrt(x), кубические корни cbrt(x)
• тригонометрические функции: синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции: арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x), десятичные логарифмы log(x)
• гиперболические функции: гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции: asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,помогите рассказать об этом сайте:

Пределы в жизни

Пределы из математики часто используются для решения практических задач, где нужно найти точку, после которой разница в результате будет уже незаметна.

Например, бригада монтажников строит мост, и им нужно понять, какой максимальной длины можно сделать плиту перекрытия. Есть требования, что плита должна выдерживать в середине нагрузку в 50 тонн — она может быть и прочнее, но 50 тонн это минимум. Для решения этой задачи используют предел — он покажет, длиннее какого размера делать плиту нельзя, а всё, что короче, даст необходимую прочность.

Астрономы с помощью пределов изучают законы Вселенной, физики проверяют всё на прочность, и даже в микроэлектронике затухание сигналов тоже зависит от пределов функций.

Предел функции

Предел функции при

Пусть функция f(x) определена на некотором множестве X и
пусть дана точка .
Возьмём из X последовательность точек, отличных от :

   (1)

сходящуюся к .
Значения функции в точках этой последовательности также образуют числовую последовательность

   (2)

и можно ставить вопрос о существовании её предела.

Определение 1. Число A называется пределом функции f(x)
в точке (или при ),
если для любой сходящейся к последовательности (1)
значений аргумента x, отличных от ,
соответствующая последовательность (2) сходится к числу A.

Символически это записывается так:

Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.

Пример 1. Найти предел функции при .

Решение. Подставляем вместо x значение 0. Получаем:

.

Итак, предел данной функции при равен 1.

Кроме того, решённые в этом уроке примеры и любые другие задачи на
пределы, можно на проверить на калькуляторе пределов
онлайн.

Предел функции при , при и при

Кроме рассмотренного понятия предела функции при
существует также понятие предела функции при стремлении аргумента к бесконечности.

Определение 2. Число A называется пределом функции f(x)
при ,
если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2)
значений функции сходится к A.

Символически это записывается так: .

Определение 3. Число A называется пределом функции f(x)
при (),
если для любой бесконечно большой последовательности значений аргумента, элементы
которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.

Символически это записывается так: ().

Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.

Пример 2. Найти предел функции при .

Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:

.

Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.

А проверить решение задачи на
пределы можно на калькуляторе пределов
онлайн.

Как решать пределы для чайников?

Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.

Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения

Слайды и текст этой презентации

Слайд 1ВЫСШАЯ МАТЕМАТИКА ПРЕДЕЛЫ. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
Работу выполнили:Сидорова АнжелаСоловьева НатальяЗахарова ОльгаСафонова ВикторияПискунова

Понятие предела использовалось еще Ньютоном во второй половине XVII века

и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела дали Больцано в 1816 году и Коши в 1821 году.

Слайд 41. ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫПусть переменная величина x в процессе своего

изменения неограниченно приближается к числу 5, принимая при этом следующие

значения: 4,9; 4,99;4,999;…или 5,1; 5,01; 5,001;… В этих случаях модуль разности стремится к нулю: = 0,1; 0,01; 0,001;… Число 5 в приведенном примере называют пределом переменной величины x и пишут lim x = 5.Определение 1. Постоянная величина a называется пределом переменной x, если модуль разности при изменении x становится и остается меньше любого как угодно малого положительного числа e.

Слайд 52. ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ 1. Предел алгебраической суммы конченного числа переменных

величин равен алгебраической сумме пределов слагаемых: lim(x + y + …

+ t) = lim x + lim y + … + lim t. 2. Предел произведения конечного числа переменных величин равен произведению их пределов: lim(x·y…t) = lim x · lim y…lim t. 3. Постоянный множитель можно выносить за знак предела: lim(cx) = lim c · lim x = c lim x.Например, lim(5x + 3) = lim 5x + lim 3 = 5 lim x + 3. 4. Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен нулю: lim = lim y 5. Предел целой положительной степени переменной величины равен той же степени предела этой же переменной: lim = (lim x)nНапример: = = x3 + 3 x2 = (-2)2 + 3·(-2)2 = -8 + 12 = 4 6. Если переменные x, y, z удовлетворяют неравенствам x и x z y

Слайд 63.ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Определение 2. Число b называется пределом* функции

в точке a, если для всех значений

x, достаточно близких к a и отличных от a, значения функции сколь угодно мало отличаются от числа b. 1.Найти: (3×2 – 2x). Решение. Используя последовательно свойства 1,3 и 5 предела, получим (3×2 – 2x) = (3×2) — (2x) = 3 x2 — 2 x = 3 — 2 x = 3 22 — 2·2 = 8

Слайд 74. ПОНЯТИЕ О НЕПРЕРЫВНОСТИ ФУНКЦИИ
2. ВычислитьРешение. При x = 1

дробь

определена, так как ее знаменатель отличен от нуля. Поэтому для вычисления предела достаточно заменить аргумент его предельным значением. Тогда получимУказанное правило вычисления пределов нельзя применять в следующих случаях: 1)Если функция при x = a не определена; 2)Если знаменатель дроби при подстановке x = a оказывается равным нулю; 3)Если числитель и знаменатель дроби при подстановке x = a одновременно оказывается равным нулю или бесконечности.В таких случаях пределы функций находят с помощью различных искусственных приемов.

Слайд 85. ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ3.Найти Решение. При x

знаменатель х + 5 также стремится к бесконечности, а обратная

ему величина 0. Следовательно, произведение · 3 = стремится к нулю, если x . Итак, = 0

Слайд 96. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
Некоторые пределы невозможно найти теми способами, которые были

изложены выше. Пусть например, требуется найти

. Непосредственная подстановка вместо аргумента его предела дает неопределенность вида 0/0. Невозможно также преобразовать числитель и знаменатель таким образом, чтобы выделить общий множитель, предел которого равен нулю. Поступим следующим образом. Возьмем круг с радиусом, равным 1, и построим центральный угол АОВ, равный 2х радианам. Проведем хорду АВ и касательные АD и ВD к окружности в точках А и В. Очевидно, что |AC| = |CB| = sin x, |AD| = |DB| = tg х = 1 – Первый замечательный предел. x = e 2,7182…,.  x – Второй замечательный предел.Решение. Разделив числитель и знаменатель на x,получим x = ( )x = = =

Слайд 107. ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ

1. (x2 – 7x

+ 4) = 32 – 7·3 + 4 = —

8.Решение. Для нахождения предела непосредственного нахождения заменим пределы функции в точке.2. .Решение. Здесь пределы числителя и знаменателя при x равным нулю. Умножим числитель и знаменатель на выражение ,сопряженное числителю, получим = = = = Следовательно,

=

=

=

=

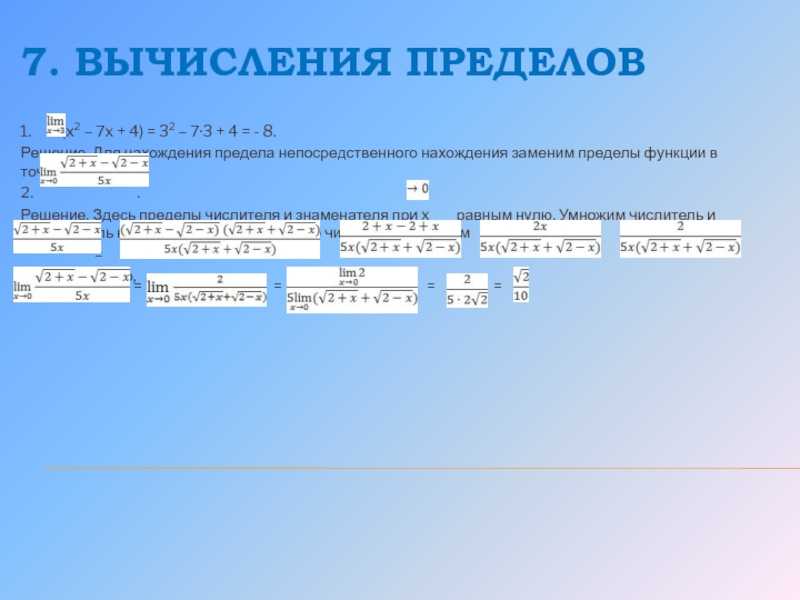
Слайд 11ЗАКЛЮЧЕНИЕ В данном проекте рассматривался наряду с теоретическим материалом и практический. В

Считаем предел в программировании

Раз у нас есть постоянное действие по уменьшению или увеличению переменной, то логично сделать из этого простой цикл и поручить его машине. Единственное, что нам нужно предусмотреть, — момент, когда цикл должен остановиться, потому что в мире математики lim по умолчанию касается бесконечности (потому что стремиться можно бесконечно).

Так как мы не знаем заранее точного предела функции, но можем контролировать количество повторений, то сделаем такие условия для остановки цикла:

1. Закончилось количество повторений. Например, мы заранее говорим, что будем стремиться к границе предела 10000000000 раз, но если ничего не выйдет — остановимся.
2. Если достигли нужной погрешности. Два соседних результата отличаются на величину погрешности или меньше — отлично, мы нашли то, что нужно.

Самый сложный момент в коде — описать то, как переменная функции к чему-то стремится. Если к бесконечности, то всё просто: на каждом шаге прибавляем или умножаем на какое-то число. А если нужно, чтобы переменная стремилась к нулю или другому числу, то можно действовать так: брать начальное число, конечное, складывать их и делить пополам. Так мы будем постоянно приближаться к нужному нам числу, но никогда его не достигнем.

Важная оговорка: числа в компьютере — это не числа в абстрактном математическом понимании, а конечный набор данных. Конечный он тем, что на всякое число выделяется какое-то количество «клеток», в которые это число можно записать. Если у нас ограниченное количество «клеток», значит, у нас есть какой-то предел самого большого и самого малого числа.

Например, если мы дали переменной 32 бита памяти, самое малое число, которое мы сможем в нее записать, — 1,4012985 × 10-45. Это кажется бесконечно малым, но на самом деле, если циклически делить число на 2 несколько сотен раз в секунду, мы упремся в этот лимит точности почти сразу. Потом знаки после запятой закончатся и число очень быстро превратится в 0.

С точки зрения математики любое число можно бесконечно делить и получать бесконечное число знаков после запятой; а с точки зрения компьютера бесконечное число знаков невозможно, и если делить достаточно долго — мы получим ноль.

Поэтому в работе с пределами важно указывать либо число шагов для определения предела, либо погрешность. Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

Теперь напишем простой цикл, который нам посчитает lim x→2 (8−2x) / (x²−4x−12):

• предел функции f(x) = (8−2x) / (x²−4x-12);
• при x стремящемся к 2.

Если мы посчитаем этот предел как математики, то получим значение −1. Проверим, как с этим справится наш код:

1. // погрешность вычислений var e = 0.00001;
2. // предел, к которому будет стремиться переменная var lim = 2; // переменная функции, на старте начинаем стремиться к пределу отсюда var x = 0;
3. // сколько раз мы уже выполнили цикл var n = 0;
4. // максимальное количество приближений к пределу var max_n = 100;
5. // функция, которая возвращает значение для переменной функции function f(x) { return (8 — 2*x*x)/(x*x + 4*x — 12); }
6. // пока мы не достигли нужной погрешности — выполняем цикл while (Math.abs(f(x) -f((x+lim)/2)) >= e) { // приближаемся ещё на один шаг к пределу x = (x+lim)/2;
7. // увеличиваем счётчик приближений n +=1;
8. // если дошли до максимального количества повторений if (n == max_n) { // выводим сообщение о том, что останавливаемся console.log(‘Закончилось количество повторений, остановились на таком значении функции: ‘, f(x));
9. // сбрасываем переменную с максимальным значением повторений и выходим из цикла max_n = 0; break; } } // если переменная с максимальным значением не была сброшена if (max_n != 0){ // выводим найденный предел console.log(‘Предел функции с заданной погрешностью: ‘, f(x)) }
   Программа справилась и выдала результат с нужной нам точностью