Разряды чисел
Положение цифры в записи числа определяет его значение. Например:
1123 содержит: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.
Можно сформулировать иначе и сказать, что в данном числе 1123 цифра 3 стоит в разряде единиц, 2 – в разряде десятков, 1 – в разряде сотен, а 1 служит значением разряда тысяч.
Поясним, что такое категория в математике. Цифра — это расположение или расположение цифры в записи натурального числа.
Каждая категория имеет свое название. Старшие цифры всегда живут слева, а младшие цифры всегда живут справа. Чтобы быстрее запомнить, можно воспользоваться таблицей.

Количество цифр всегда соответствует количеству символов в номере. В этой таблице есть названия всех цифр для числа, состоящего из 15 символов. Следующие цифры тоже имеют названия, но используются они редко.
Младшая (наименее значащая) цифра в многозначном натуральном числе — это цифра единиц.
Старшей (старшей) цифрой в многозначном натуральном числе является цифра, соответствующая самой левой цифре данного числа.
Битовые единицы обозначаются следующим образом:
- Единицы — единицы первой цифры (или простые единицы) и пишутся изначально справа.
- Десятки являются единицами второго разряда и записываются в числе вторыми справа.
- Сотни – это единицы третьего разряда и пишутся третьими справа.
- Единицы тысячи — это единицы четвертой цифры, которые записываются четвертой справа.
- Десятки тысяч являются единицами пятой цифры и записываются пятой справа.
- Сотни и тысячи являются единицами шестого разряда и записываются в числе шестым справа и так далее.
Каждая третья последовательная цифра представляет собой класс. Первые три цифры: единицы, десятки и сотни образуют класс единиц (первый класс). Следующие три цифры: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будет единицами, десятками и тысячами миллионов и так далее.
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
- Единица (1) — самое маленькое число, а самого большого числа не существует.
- Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Отличия числа от цифры
- С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
- Число может быть отрицательным, дробным, в отличие от цифр.
- Количество арабских цифр всего 10 (римских — 7), а чисел — бесконечное множество, т.к. они состоят из цифр.
Надеюсь, что теперь вам всё понятно, и вы сможете без труда объяснить даже ребёнку, чем отличается число от цифры.
На уроках математики в начальной школе используется очень полезное упражнение. Детей просят дать характеристику числу. Другими словами рассказать о числе все, что знаешь. Не всем детям это задание даётся легко. Чтобы его выполнить пригодятся вышеописанные знания и не только.
Что такое число
Число — это математический инструмент, представляющий количество «моделей». Чтобы понять, что такое модель, представьте себе стол на четырех ножках. Цифра 4 обозначает кости, каждая кость состоит из разных кусочков материала, у них есть свои трещины, но главное, что это кости. Берем не конкретную ногу, а идеальную модель ноги. Цифра 4 показывает количество этих шаблонов.
Математика упрощает реальные объекты до идеальных моделей, отбрасывая лишнее и сосредотачиваясь на существенном. Это число и есть идеальная модель, точнее количество этих моделей. Он дает силу понимания и мы не складываем золото с ракушками.
Также важно знать: один и тот же объект может быть выражен разными числами, это зависит от наших задач. Дерево можно представить как: 1000 ветвей или 50 000 листьев или 100 литров кислорода в день
Число – это количество идеальных моделей.
Системы счисления
Система счисления – это некий вариант представления чисел.
К примеру, представьте, что перед вами лежит несколько яблок. Вы хотели бы узнать, сколько яблок лежат на столе? Для этого вы могли бы считать, загибая пальцы рук или делать зарубки на дереве. А могли бы вы и представить, что десять яблок – это одна корзинка, а одно яблоко – это одна спичка. Спички по ходу счета выкладывать на столе под одной.
В первом варианте подсчета число получилось в виде строки из зарубок на дереве (или загнутых пальцев рук), а во втором варианте подсчета – это был набор из корзинок и спичек. Слева должны быть емкости, а справа — спички.
Системы счисления бывают двух видов:
- Позиционные.
- Непозиционные.
Позиционные системы счисления бывают:
- Однородными.
- Смешанными.
Непозиционной называют такую систему счисления, в которой цифра в числе соотносится с такой величиной, которая не зависит от ее разряда. Поэтому, если у вас пять зарубок, то число будет равно пяти. Ибо каждой зарубке будет соответствовать одно яблоко.
Позиционной системой счисления является та, в которой цифра в числе будет зависеть от ее разряда.
Та система счисления, к которой мы привыкли – это десятичная система счета. Она позиционная.
Когда наши предки начали учиться считать, у них появилась идея записывать числа. изначально они использовали те самые зарубки на деревьях или камнях, где каждая черточка обозначала какой-либо предмет (одно яблоко, к примеру). Именно так и была изобретена единичная система счисления.
Число в философии[]
Философское понимание числа заложили пифагорейцы. Аристотель свидетельствует, что пифагорейцы считали числа «причиной и началом» вещей, а отношения чисел основой всех отношений в мире. Числа придают миру упорядоченность и делают его космосом. Такое отношение к числу было принято Платоном, а позже неоплатониками. Платон при помощи чисел различает подлинное бытиё (то, что существует и мыслится само по себе), и неподлинное бытиё, (то, что существует лишь благодаря другому и познаётся только в отношении). Срединное положение между ними занимает число. Оно придаёт меру и определённость вещам и делает их причастными бытию. Благодаря числу вещи могут быть подвергнуты пересчёту и поэтому они могут быть мыслимы, а не только ощущаемы. Неоплатоники, особенно Ямвлих и Прокл, почитали числа столь высоко, что даже не считали их сущими — устроение мира исходит от числа, хотя и не непосредственно. Числа сверхсущны, пребывают выше Ума, и недоступны знанию. Неоплатоники различают божественные числа (прямую эманацию Единого) и математические числа (составленные из единиц). Последние являются несовершенными подобиями первых. Аристотель, наоборот, приводит целый ряд аргументов, показывающих, что утверждение о самостоятельном существовании чисел приводит к нелепостям. Арифметика выделяет в этих реально сущих вещах только один аспект и рассматривает их с точки зрения их количества. Числа и их свойства являются результатом такого рассмотрения. Кант считал, что явление познано тогда, когда оно сконструировано в соответствии с априорными понятиями — формальными условиями опыта. Число — одно из таких условий. Число задаёт конкретный принцип или схему конструирования. Любой объект является исчислимым и измеряемым, потому что он сконструирован по схеме числа (или величины). Поэтому всякое явление может рассматриваться математикой. Разум воспринимает природу подчинённой числовым закономерностям именно потому, что сам строит её в соответствии с числовыми закономерностями. Так объясняется возможность применения математики в изучении природы. Математические определения, разработанные в 19 веке, были серьёзно пересмотрены в начале 20 века. Это было вызвано не столько математическими, сколько философскими проблемами. Определения, которые были даны Пеано, Дедекиндом или Кантором, и которые используются в математике и в настоящее время, нужно было обосновать с помощью фундаментальных принципов, коренящихся в самой природе знания. Различают три таких философско-математических подхода: логицизм, интуиционизм и формализм. Философскую базу логицизма разработал Рассел. Он полагал, что истинность математических аксиом неочевидна. Истинность обнаруживается сведением к наиболее простым фактам. Отражением таких фактов Рассел считал аксиомы логики, которые он положил в основу определения числа. Важнейшим понятием у него является понятие класса. Натуральное число η есть класс всех классов, содержащих η элементов. Дробь — это уже не класс, а отношение классов. Интуицист Брауэр имел противоположную точку зрения: логику он считал лишь абстракцией от математики, рассматривал натуральный ряд чисел как базовую интуицию, лежащую в основании всякой мыслительной деятельности. Гильберт, главный представитель формальной школы, видел обоснование математики в построении непротиворечивой аксиоматической базы, в пределах которой можно бы было формально обосновать любое математическое понятие. В разработанной им аксиоматической теории действительных чисел представление о числе лишается всякой глубины и сводится лишь к графическому символу, подставляемому по определённым правилам в формулы теории.
Представление чисел в памяти компьютера
Чтобы представить положительное целое число xi в памяти компьютера, оно преобразуется в двоичную систему счисления. Полученное число в двоичном формате x2 представляет собой машинную запись соответствующего десятичного числа x10. Запись отрицательных чисел, так называемый дополнительный код числа, который получается прибавлением единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.
Представление действительных чисел в памяти ЭВМ (в вычислительной технике для их обозначения используется термин с плавающей запятой) имеет некоторые ограничения, связанные с используемой системой счисления, а также с ограниченным объемом памяти, выделяемой под числа. Таким образом, только часть действительных чисел может быть точно представлена в памяти компьютера без потерь. В наиболее распространенной форме число с плавающей запятой записывается как блок битов, некоторые из которых являются мантиссом числа, некоторые — степенью, а один бит назначается для представления знака числа (если необходимо, бит знака может отсутствовать).
Классы чисел
Цифры в записи многозначных чисел делятся справа налево на группы по три цифры в каждой. Эти группы называются классами. В каждом классе числа справа налево представляют единицы, десятки и сотни этого класса.
Таблица класса:
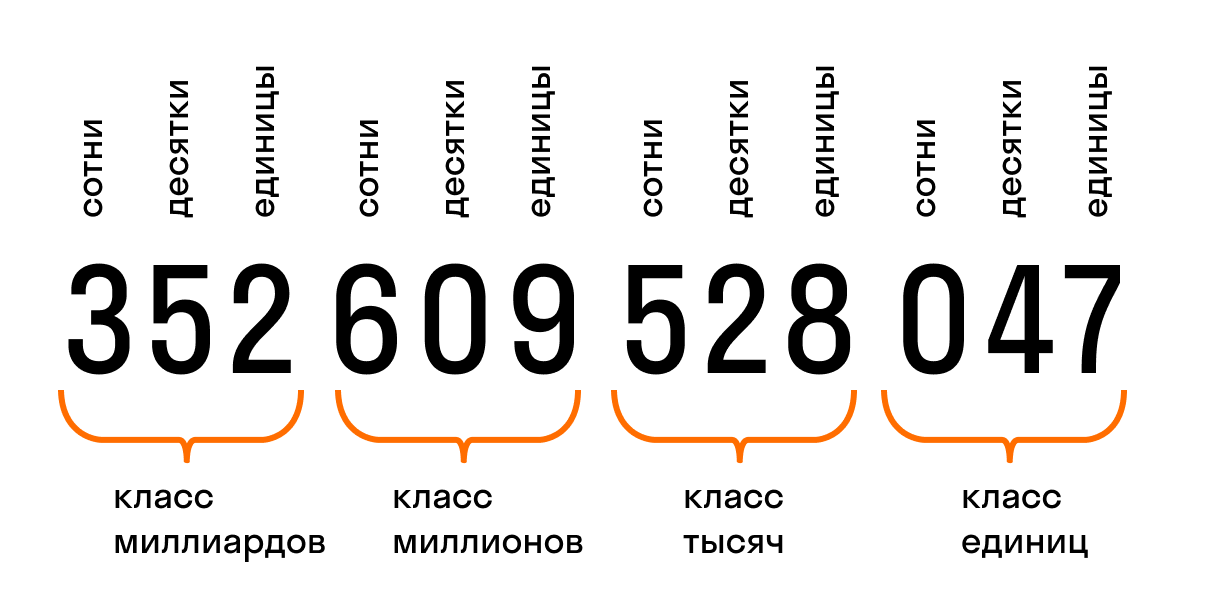
Названия классов с многозначными числами справа налево:
- первый — это класс сущностей,
- другой — класс тысяч,
- третий — класс миллионов,
- четвертый — класс миллиардов,
- пятый — класс триллионов,
- шестой класс квадриллион,
- седьмой класс квинтиллионов,
- восьмой — класс секстиллионов.
Чтобы было удобно читать запись многозначного числа, между классами есть небольшой промежуток. Например, чтобы прочитать число 125911723296, удобно сначала извлечь в нем классы:
125 911 723 296.
А теперь читаем количество единиц в каждом классе слева направо:
125 миллиардов 911 миллионов 723 тысячи 296.
При чтении класса единиц не нужно добавлять в конце слово «единицы.
Принцип образования чисел
С помощью десяти цифр можно записать любое натуральное число. В зависимости от того, сколько цифр содержится в числе, оно может быть:
- однозначным – состоит из одной цифры (например: 2, 6, 7). Самое маленькое однозначное число – это единица, самое большое – 9.
- двузначным – состоит из двух цифр (например: 14, 52, 60, 78 и т.д.). Самое маленькое двузначное число – это 10, самое большое – 99.
- трехначным – содержит три цифры (например: 184, 211, 306, 612 и т.д.). Наименьшее трехзначное число – 100, наибольшее – 999.
- четырехзначным, пятизначным или, другими словами, многозначным (например: 2048, 51947, 984871 и т.д.). В соответствии с названием, такие числа состоят из четырех, пяти, шести и большего количества цифр.
Примеры:
1. Число “пятьдесят восемь” пишется так – “58”. То есть мы расставляем цифры по соответствующим разрядам:
- “8” – в единицах;
- “5” – в десятках.
2. Чтобы записать число “шестьсот двадцать шесть” нам нужны только две цифры – “6” и “2”, несмотря на то, что оно трехзначное:
- “6” – в единицах и сотнях;
- “2” – в десятках.
Т.е. получается “626”.
Использование запятой
Для записи чисел могут использоваться не только цифры, но и запятые (в некоторых странах – точки). Делается это для отделения целой и дробной частей. Например:
- 120,5
- 306,71
- 221,409
Определение, запись, произношение и свойства десятичной дроби мы подробно рассмотрели в отдельной публикации.
Произношение чисел
Числа от 1 до 20
| Число | Произношение | Число | Произношение |
| 1 | один | одиннадцать | одиннадцать |
| 2 | два | 12 | двенадцать |
| 3 | три | 1. 3 | тринадцать |
| 4 | четыре | 14 | четырнадцать |
| 5 | пять | 15 | пятнадцать |
| 6 | шесть | 16 | шестнадцать |
| 7 | семь | 17 | семнадцать |
| 8 | восемь | 18 | восемнадцать |
| 9 | девять | 19 | девятнадцать |
| 10 | десять | 20 | двадцать |
Десятки и сотни
| Число | Произношение | Число | Произношение |
| 10 | десять | 100 | сто |
| 20 | двадцать | 200 | двести |
| 30 | тридцать | 300 | три сотни |
| 40 | сорок | 400 | четыре сотни |
| 50 | пятьдесят | 500 | пятьсот |
| 60 | шестьдесят | 600 | шестьсот |
| 70 | семьдесят | 700 | семь сотен |
| 80 | восемьдесят | 800 | восемьсот |
| 90 | девяносто | 900 | девятьсот |
Степени 10
| Число | Произношение | 10 вечера |
| 1000 | тысяча | 103 |
| 1 000 000 | миллион | 106 |
| 1 000 000 000 | миллиарды | 109 |
| 1 000 000 000 000 | триллионы | 1012 |
| 1 000 000 000 000 000 | квадриллион | 1015 |
| 1 000 000 000 000 000 000 | квинтиллион | 1018 |
| 1 000 000 000 000 000 000 000 | секстиллион | 1021 |
| 1 000 000 000 000 000 000 000 000 | септиллион | 1024 |
| 1 000 000 000 000 000 000 000 000 000 | октиллион | 1027 |
| 1 000 000 000 000 000 000 000 000 000 000 | квинтиллион | 1030 |
| 1 000 000 000 000 000 000 000 000 000 000 000 | дециллион | 1033 |
Названия чисел после 20 составные, т.е все цифры в каждом классе произносятся по очереди с добавлением названия самого класса (от старшего к младшему), за исключением первого класса.
Примеры:
- 65 — «шестьдесят пять”;
- 247 — «двести сорок семь”;
- 1 518 — «одна тысяча пятьсот восемнадцать”;
- 25 814 — «двадцать пять тысяч восемьсот четырнадцать”;
- 450 627 – «четыреста пятьдесят тысяч шестьсот двадцать семь”;
- 2 393 026 — «два миллиона триста девяносто три тысячи двадцать шесть”.
Что такое цифра?
Это вопрос, на который мы получаем ответ изначально от родителей, потом от преподавателей в учебных заведениях. Что такое цифра? А из словаря Владимира Даля можно узнать, что цифры — это численные показатели. Именно они представляются символами чисел. Нам известно всего 10 цифр: от нуля до девяти. Из их сочетания получается бесконечность чисел. Какие же существуют цифры?
- Арабские. Такими символами мы пользуемся довольно-таки давно. Они возникли в Европе еще в 10-м веке.
- Римские. Возникли еще за пять веков до нашей эры и находились в обиходе у племен этрусков, проживавших на Апеннинском полуострове.
- Цифры майя. Такие знаки использовались для расчетов в календаре.
Но в современном мире цифра — это не только математический знак, и сегодняшний день существует даже цифровое телевидение, а также существует цифровой формат.

Как дать характеристику числу?
Разберём несколько примеров.
Число 7 — однозначное, нечетное, соседи числа 7 числа 6 и 8.
Также чисел первого десятка можно добавить такое дополнительное задание, как состав числа. Т.е. число 7 можно получить сложением чисел 1 и 6, 2 и 5, 3 и 4.
Число 10 — двузначное, чётное, круглое, соседи числа 9 и 11. Число 10 можно получить сложением чисел 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5.
Чем крупнее число, тем больше можно о нём рассказать.
Число 999 — наибольшее трёхзначное число, нечётное, соседи 998 и 1000, в числе 9 сотен, 9 десятков и 9 единиц.
Надеюсь, что полученные знания были вам полезны и теперь вы знаете чем отличается цифра от числа, сможете объяснить это ребёнку простыми словами, а также потренироваться давать характеристику числам.
Что правило нам расскажет?
Вспоминаем, как пишутся буквы «и», «ы» после согласной «ц».
А правило нам говорит, что гласная «И» пишется в корнях слов:
-
Цистит.
-
Цинга.
-
Циркуль.
В словах с окончанием «ция»:
-
Корпорация.
-
Революция.
-
Авиация.
Буква «ы» пишется в случае, если у нас есть суффикс «ын»:
-
Сестрицын.
-
Синицын.
В окончании существительных во множественном числе:
-
Курицы.
-
Улицы.
-
Пепельницы.
А еще у нас есть слова-исключения, в их корнях всегда будет писаться буква «ы»:
Цыган, цыкнуть, цыц, цыпленок, цыпочки.
Возвращаясь к тому, как же правильно, писать — цыфра или цифра? Давайте хорошенько подумаем. Это слово входит в число слов-исключений? Нет. Оно стоит во множественном числе? Тоже нет. Это суффикс, оканчивающийся на «цын»? И этот вариант отпадает.
Значит что остается? Правописание гласной «и». Она, как мы выяснили, пишется в корнях слова. В нужном нам слове корень «цифр». Пишем цифра или цыфра? Разумеется, первый вариант, согласно правилам русского языка.
Разница между цифрами и числами
После того как мы узнали, что такое цифра и что такое число, пора узнать, в чем разница между двумя этими математическими понятиями:
- С числами можно проводить множество математических действий, чего невозможно сделать с цифрами.
- По сравнению с цифрами, числа бывают отрицательными.
- Чисел существует огромное количество, а вот цифр десять.
Помимо математических различий, существуют также лингвистическая разница. Они подразумевают под собой ситуации, когда следует использовать слово «цифра», а когда стоит сказать «число». В диалоге, где упоминаются официальные данные, скажем так, статистические показатели, уместно будет сказать слово «цифра». Это понятие больше используется в нумерологии. Ученные считают, что этот знак может повлиять на судьбу человека, так как он наделен магическими свойствами.
Слово «число» употребляется тогда, когда необходимо указать величину, или же когда речь заходит о каких-либо календарных датах. В русском языке чаще употребляются порядковые числительные.

Основные классы чисел[]
Натуральные числа, получаемые при естественном счёте; множество натуральных чисел обозначается N{\displaystyle \mathbb {N} }. То есть N={1,2,3,…}{\displaystyle \mathbb {N} =\left\{1,2,3,…\right\}} (иногда к множеству натуральных чисел также относят ноль, то есть N={,1,2,3,…}{\displaystyle \mathbb {N} =\left\{0,1,2,3,…\right\}}). Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Сложение и умножение натуральных чисел коммутативны и ассоциативны, а умножение натуральных чисел дистрибутивно относительно сложения и вычитания.
Важным подмножеством натуральных чисел являются простые числа P.{\displaystyle \mathbb {P} .} Простое число — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и самого себя. Все остальные натуральные числа, кроме единицы, называются составными. Ряд простых чисел начинается так: 2,3,5,7,11,13,17,…{\displaystyle 2,3,5,7,11,13,17,…} Любое натуральное число, большее единицы, представимо в виде произведения степеней простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Например, 121968=24·32·7·112.
Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются Z={…−2,−1,,1,2,…}{\displaystyle \mathbb {Z} =\left\{…-2,-1,0,1,2,…\right\}}. Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления).
Рациональные числа — числа, представленные в виде дроби m/n (n≠0), где m — целое число, а n — натуральное число. Рациональные числа замкнуты уже относительно всех четырёх арифметических действий: сложения, вычитания, умножения и деления (кроме деления на ноль). Для обозначения рациональных чисел используется знак Q{\displaystyle \mathbb {Q} } (от лат. quotient).
Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается R{\displaystyle \mathbb {R} }. Его можно рассматривать как пополнение поля рациональных чисел Q{\displaystyle \mathbb {Q} } при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, R{\displaystyle \mathbb {R} } включает множество иррациональных чисел I{\displaystyle \mathbb {I} }, не представимых в виде отношения целых.
Комплексные числа C{\displaystyle \mathbb {C} }, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z=x+iy{\displaystyle z=x+iy}, где i — т. н. мнимая единица, для которой выполняется равенство i2=−1{\displaystyle i^{2}=-1}. Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики, теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Более общими (но всё ещё счётными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).
Для перечисленных множеств чисел справедливо следующее выражение: P⊂N⊂Z⊂Q⊂R⊂C.{\displaystyle \mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} .}
|
||||||||||||||||||||
| 1,e1,e2,…,e15,7e2+25e7−13e15,…{\displaystyle 1,\;e_{1},\;e_{2},\;\dots ,\;e_{15},\;7e_{2}+{\frac {2}{5}}e_{7}-{\frac {1}{3}}e_{15},\;\dots } | Седенионы |
Единичная система счисления
Различие между цифрой и числом в единичной системе счисления в том, что число в этом случае равнозначно строке, состоящей из палочек. Количество палочек (зарубок на дереве) равняется значению числа.
К примеру, урожай из 50 яблок будет равен числу, состоящему из 50 палочек (черточек, зарубок).
Сколько цифр содержит число 50? Две цифры. Цифра 0 и цифра 5. Но количество яблок гораздо больше двух.
Основное неудобство в этой системе счисления – слишком длинная строка из черточек. А если бы урожай составлял 5 000 яблок? Действительно, записывать такое число неудобно. Прочтение тоже будет вызывать затруднения.
Поэтому позже наши предки научились группировать черточки по несколько штук (по 5, 10). И для каждой объединяющей группы был придуман специальный знак. Сначала для 5 и 10 использовали пальцы рук. А затем были придуманы определенные символы. Таким способом считать яблоки стало гораздо проще.




























