Разрядные слагаемые. представление числа в виде суммы разрядных слагаемых

Разряды и классы чисел

Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.

В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют Классами.

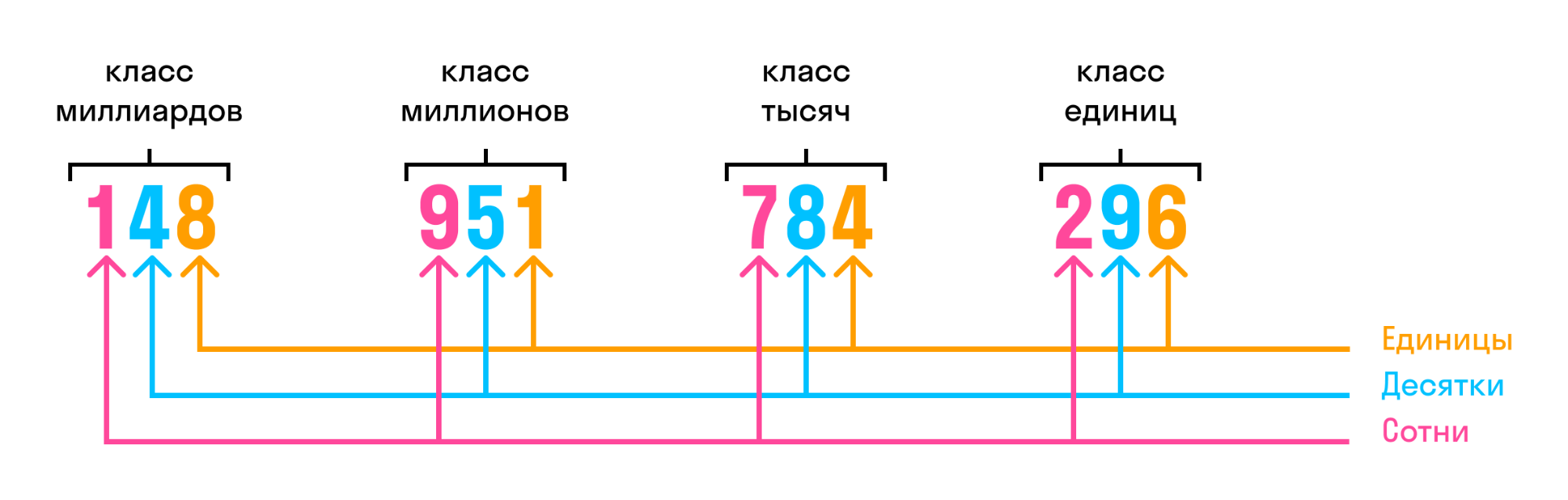
Названия классов многозначных чисел:

Первый — класс единиц,

Второй — класс тысяч,

Третий — класс миллионов,

Четвёртый — класс миллиардов,

Пятый — класс триллионов,

Шестой — класс квадриллионов,

Седьмой — класс квинтиллионов,

Восьмой — класс секстиллионов.

Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:

345 466 129 350 вместо 345466129350

Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.

Разряд — это место, которое занимает цифра в записи многозначного числа.

Разряды считаются справа налево. Первая цифра справа в записи числа относится к Первому разряду.

• Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.

Разрядные единицы — это единицы, десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллионы и т. д.

Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.

10 единиц = 1 десяток;

10 десятков = 1 сотня;

10 сотен = 1 тысяча;

10 тысяч = 1 десяток тысяч;

10 десятков тысяч = 1 сотня тысяч;

10 сотен тысяч = 1 миллион.

Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.

Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.

Например, нужно сказать, сколько сотен в числе 5689.

Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. Мысленно вычеркиваем разряды правее сотен, остается две цифры: 56. Значит, в числе 5689 56 сотен.

Если в разряде стоит цифра 0 — это означает отсутствие единиц данного разряда.

Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.

В такой ситуации можете выполнить подробный разбор числа.

Разберем число 6 057 386

Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть

6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.

Из чего состоит это число? Из:

Шести единиц миллионов (6 * 1 000 000);

Пяти десятков тысяч (5 * 10 000);

Семи единиц тысяч (7 * 1000);

Трех сотен (3 * 100);

Восьми десятков (8 * 10);

Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.

Определите, сколько единиц каждого разряда в числе 5 068 252.

1. Определяем сколько всего Единиц в числе.

2. Определяем количество Десятков.
Записываем число без первого разряда (единицы).

3. Определяем количество Сотен.
Записываем число без первого
И второго разрядов (десятки и сотни).

4. Определяем количество Единиц тысяч.
Записываем число без первого, второго,
Третьего разрядов (единицы, десятки, сотни).

5. Определяем количество Десятков тысяч.
Записываем число без первого, второго, третьего,
Четвертого разрядов (единицы, десятки, сотни, единицы тысяч).

6. Определяем количество Сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
Сотен и единиц.

7. Определяем количество Единиц миллионов.

Записываем число без сотен тысяч, десятков тысяч,
Единиц тысяч, сотен, десятков, единиц.

Расписав таким образом число, мы выяснили, что в числе 5 068 252 содержится 5 миллионов, 50 сотен тысяч, 506 десятков, 5068 тысяч, 50 682 сотни, 506 825 десятка, 5 068 252 единицы.

А если разобрать число по классам, то можно сказать, что число 5 068 252 содержит 5 единиц класса миллионов (третий класс), 68 единиц класса тысяч (второй класс), 252 единицы класса единиц (первый класс).

Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.

Классы и разряды чисел-математика | Таблица классов и разрядов

Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

С помощью десяти цифр можно записать любое натуральное число.

Натуральные числа

От количества знаков (цифр) в числе зависит его название:

• Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число — «1» , наибольшее — «9».
• Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — «10», наибольшее — «99» .
• Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — «100», наибольшее — «999».

Запомните! Каждая цифра в записи многозначного числа занимает определённое место — позицию.

Разрядность чисел

Разряд — это место (позиция), на котором в записи числа стоит цифра.

Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.

Разряды отсчитываются с конца числа.

Разряд единиц — это самый младший разряд, которым заканчивается любое число.

Цифра «5» — означает «5» единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).

Разряд десятков — это разряд, который стоит перед разрядом единиц.

Цифра «5» — означает «5» десятков, если она стоит на предпоследнем месте (в разряде десятков).

Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра «5» означает «5» сотен, если она стоит на третьем месте от конца числа (в разряде сотен).

Запомните! Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра «0» (ноль).

Пример. В числе «807» содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа.807 = 8 сотен 0 десятков 7 единиц

Читать также: Как делить столбиком

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.

Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.

Классы и разряды

В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.

Класс единиц или первый класс — это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен.

Пример 1

ЧислаКласс единиц (первый класс)СотниДесяткиЕдиницы

6	—	—	6
34	—	3	4
148	1	4	8

Класс тысяч или второй класс — это класс, который образуют следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч.

Пример 2

ЧислаКласс тысяч (второй класс)Класс единиц (первый класс)Сотни тысячДесятки тысячЕдиницы тысячСотниДесяткиЕдиницы

5 234	—	—	5	2	3	4
12 893	—	1	2	8	9	3
356 149	3	5	6	1	4	9

Напоминаем, что 10 единиц разряда сотен (из класса единиц) образуют одну тысячу (единицу следующего разряда: единицу тысяч в классе тысяч).10 сотен = 1 тысяча

Класс миллионов или третий класс — это класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов и сотни миллионов.

Единица разряда миллионов — это один миллион или тысяча тысяч (1 000 тысяч). Один миллион можно записать в виде числа «1 000 000».

• Десять таких единиц образуют новую разрядную единицу — десять миллионов «10 000 000»
• Десять десятков миллионов образуют новую разрядную единицу — сто миллионов или в записи цифрами «100 000 000».
• Пример 3

Читать также: Сложение в столбик

ЧислаКласс миллионов (третий класс)Класс тысяч (второй класс)Класс единиц (первый класс)СотниДесяткиЕдиницыСотниДесяткиЕдиницыСотниДесяткиЕдиницы

8 345 216	—	—	8	3	4	5	2	1	6
93 785 342	—	9	3	7	8	5	3	4	2
134 598 721	1	3	4	5	9	8	7	2	1

Как прочитать многозначное число

1. Запомните!
2. Чтобы прочитать многозначное число, надо назвать по очереди слева направо число единиц каждого класса и добавить название класса.
3. Не произносят название класса единиц, а также название класса, все три цифры которого нули.
4. Например, число «134 590 720» читаем: сто тридцать четыре миллиона пятьсот девяносто тысяч семьсот двадцать.
5. Число «418 000 547» читаем: четыреста восемнадцать миллионов пятьсот сорок семь.

На нашем сайте для проверки своих результатов вы можете воспользоваться калькулятором разложения числа на разряды онлайн.Важно!

Чтобы легче запомнить, как читать и записывать многозначные числа, советуем использовать выше приведённую «Таблицу классов и разрядов».

Как использовать задания

Предлагаемые ниже группы заданий помогут учителю в полной мере сформировать умения, которые в итоге приведут к желаемым результатам в области развития вычислительных навыков учеников.

Упражнения могут использоваться на уроках во время устного счета, повторения пройденного материала, в момент изучения нового. Их можно предлагать для домашних заданий, во внеклассной работе. На материале упражнений учитель может организовать групповые, фронтальные и индивидуальные формы деятельности.

Многое будет зависеть от арсенала приемов и методов, которыми владеет учитель. Но регулярность использования заданий и последовательность отработки навыков – главные условия, которые приведут к успеху.

Что такое разрядные слагаемые правило

Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

С помощью десяти цифр можно записать любое натуральное число.

От количества знаков (цифр) в числе зависит его название.

Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число — 1, наибольшее — 9.

Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — 10, наибольшее — 99.

Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определённое место — позицию.

Разряд — это место (позиция), на котором в записи числа стоит цифра.

Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.

Разряды отсчитываются с конца числа.

Разряд единиц — это самый младший разряд, которым заканчивается любое число.

Цифра 5 — означает 5 единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).

Разряд десятков — это разряд, который стоит перед разрядом единиц.

Цифра 5 — означает 5 десятков, если она стоит на предпоследнем месте (в разряде десятков).

Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра 5 означает 5 сотен, если она стоит на третьем месте от конца числа (в разряде сотен).

Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра 0 (ноль).

Пример. В числе 807 содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа.

807 = 8 сотен 0 десятков 7 единиц

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.

Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.

Логические задачи

Великий ученый Михаил Васильевич Ломоносов говорил, что математику нужно любить, потому что она приводит ум в порядок. А вы, ребята, любите математику? Не пасуете перед трудными логическими задачами? Давайте попробуем разобрать несколько интересных сложных задач. Есть над чем подумать! Не спешите заглянуть в правильные ответы!

ЗАДАЧА

Учитель математики Иван Васильевич уже на пенсии. К нему в гости часто приходят школьники. Однажды ребята спросили учителя, сколько ему лет. На что Иван Васильевич хитро улыбнулся и сказал: «Будет ровно 100, если я проживу еще половину того, что уже прожил и еще один год». Подумайте и ответьте, сколько лет Ивану Васильевичу.

Решение.

В решении этой задачи будем двигаться в обратную сторону от числа 100.

Сначала отнимем «еще один год».

100 – 1 = 99 лет.

Иван Васильевич сказал, что проживет еще половину того, что уже прожил. Значит, схематически это выглядит так:

Мы получили 3 равные части.

99 : 3 = 33(года) – составляют одну часть.

Нам нужно найти две таких части.

33 ∙ 2 = 66 (лет) – Ивану Васильевичу.

Следующую задачу попробуйте решить самостоятельно.

ЗАДАЧА

Однажды разбойники нашли под старым дубом клад в большом железном сундуке. Сундук был закрыт на замок с кодом из четырех цифр. Разбойники долго бились над расшифровкой кода, но так и не смогли открыть сундук. Ребята, попробуйте расшифровать комбинацию кодового замка и открыть сундук.

• все цифры кода в сумме дают 17;
• третья цифра на 3 больше, чем первая;
• вторая цифра на 2 больше, чем четвертая;
• вторая цифра – 3.

Проверь себя.

Итак, начнем подбирать цифры для кодового замка. Их четыре: обозначим точками.

Нам нужно выполнить еще два условия: набрать в сумме 17, третья цифра на 3 больше, чем первая.

3 + 1 = 4 – сумма известных цифр.

17 – 4 = 13 – сумма неизвестных цифр.

Две оставшиеся цифры должны дать в сумме 13, и обязательно третья цифра больше первой. Рассмотрим три варианта:

4 и 9 (не подходит, 9>4 на 5)

5 и 8 (подходит, 8>5 на 3)

6 и 7 (не подходит, 7>6 на 1)

Правильный ответ:

Ребята, понравились логические задачи? Они не имеют стандартного решения. Размышляйте, используйте для решения таких задач схемы, чертежи, таблицы, рисунки. У вас обязательно все получится.

До скорых встреч! А сейчас проверьте свои знания.

Натуральные числа и их классификация

Натуральными называют естественные величины, которые используются для счета (цифры и их комбинации: 1, 2, 3, 4, 5 и так далее), а также для расстановки по очереди (порядковые числительные: первый, второй, третий, четвертый и так далее). В совокупности они образуют так называемый ряд натуральных чисел. Его обозначением служит латинская буква N.

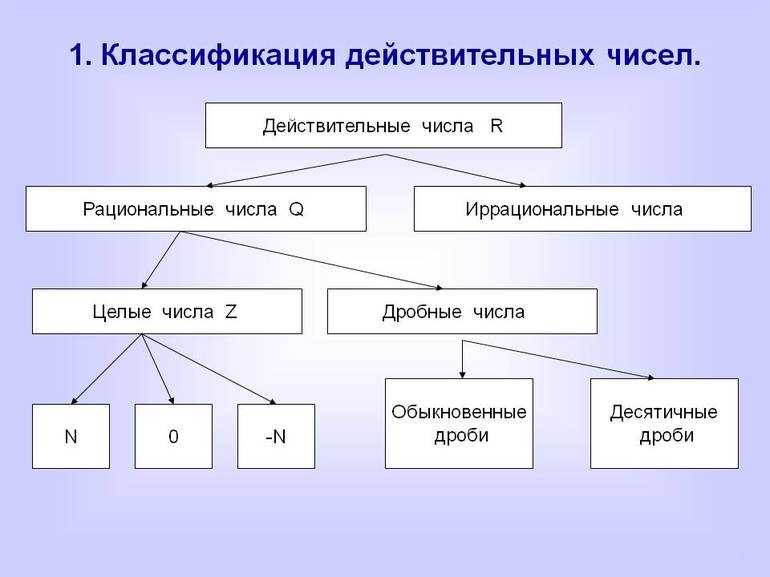
Распределение по категориям

Составляющие ряда натуральных чисел подразделяются на разряды и классы. Каждая из этих категорий неразрывно связана с другими. Разрядная классификация состоит из следующих групп (в скобках приведены слагаемые, соответствующие каждому разряду):

• единицы (1, 2, …, 9);
• десятки (10, 20, …, 90);
• сотни (100, 200, …, 900);
• тысячи (1000, 2000, …, 9000) и так далее.

Разряд числа — это положение, которое оно занимает в цифровой записи. Таким образом, любое числовое значение можно представить посредством разрядных слагаемых по математической формуле следующего вида: nnnn = n000 + n00 + n0 + n, где n означает любую цифру от 0 до 9. Для наглядного примера стоит разбить на составляющие число 4698 = 4000 + 600 + 90 + 8. Получается, что оно состоит из четырех разрядов, отображенных соответствующими составляющими:

• 4000 (четыре тысячи) — это первое слагаемое;
• 600 (шесть сотен) — второе;
• 90 (девять десятков) — третье;
• 8 (восемь простых единиц) — четвертое.

Разряд первого слагаемого называют высшим. Цифра, которой он обозначается, всегда больше нуля. Количество разрядов числа, как и количество его разрядных составляющих, всегда соответствует количеству в нем цифр, отличных от 0. Например, число 7052 состоит из трех разрядов, несмотря на свою четырехзначность. Это связано с тем, что в его составе отсутствуют сотни. Его слагаемые — семь тысяч, пять десятков и две простых единицы (7000 + 50 + 2 = 7052).

Название разрядных слагаемых обусловлено принадлежностью каждого из них к определенному разряду. Тысяча считается единицей четвертого разряда, сотня — единицей третьего разряда, десяток — второго, единица — первого. То есть нумерация разрядов начинается от наименьшей составляющей. Единицы первого разряда называются простыми, так как они однозначные. Составляющие прочих разрядов относятся к составным.

Каждый разряд состоит из десяти единиц, но обозначаться он может только девятью, так как десятая единица обеспечивает переход на следующий более высокий разряд. Не может быть разрядной составляющей типа десяти сотен — эта единица обозначается как одна тысяча.

Комплектация разрядов

В целях упрощения записи представления числа через разрядные составляющие единицы разрядов принято группировать в классы. В состав каждого из них входит три разряда:

• единицы;
• десятки;
• сотни.

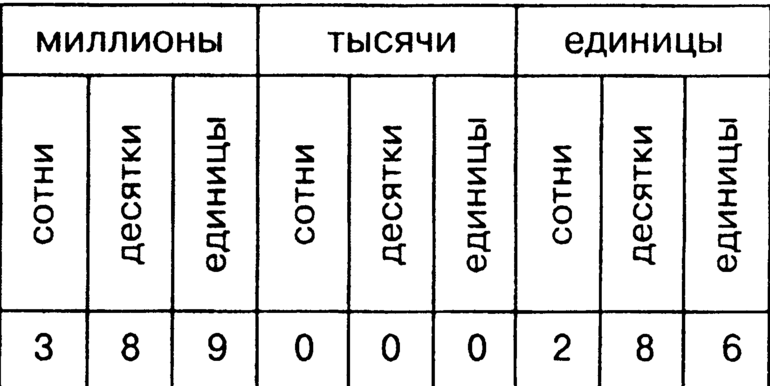
Для удобства между классами разрешается ставить пробел. Особенно это необходимо для представлений очень больших величин (от миллиона), чтобы они не выглядели бесконечным набором цифр, и в процессе их разложения не возникло путаницы. На классы число разбивается строго по три цифры справа налево.

Первый класс — это единицы. Он включает от одного до трех разрядов. Это значит, что к нему относятся все натуральные числа от 1 до 999. Второй класс — это тысячи. В него входят от четырех до шести разрядов. То есть единицы, принадлежащие к этому классу, есть во всех величинах от 1000 и больше. Дальнейшее распределение по классам:

• третий — миллионы (с седьмого по девятый разряды);
• четвертый — миллиарды (с десятого по двенадцатый);
• пятый — триллионы (с тринадцатого по пятнадцатый);
• шестой — квадриллионы (с шестнадцатого по восемнадцатый);
• седьмой — квинтиллионы (с девятнадцатого по двадцать первый) и так далее.

Распределение по классовым и разрядным категориям отображено в таблице:

Классы	Разряды
Миллиарды	сотни млрд; десятки млрд; млрд;
Миллионы	сотни млн; десятки млн; млн;
Тысячи	сотни тысяч; десятки тысяч; тысячи;
Единицы	сотни; десятки; единицы.

Примеры разрядных слагаемых чисел

Разрядные слагаемые чисел представляют собой числа, которые состоят из нескольких слагаемых, или множителей, умноженных на различные степени основания системы счисления. Давайте рассмотрим несколько примеров.

1. Десятичная система счисления:

В десятичной системе счисления разрядные слагаемые чисел представляются в виде суммы произведений цифр на степени 10.

Число	Разрядные слагаемые
123	1 * 100 + 2 * 10 + 3 * 1
6789	6 * 1000 + 7 * 100 + 8 * 10 + 9 * 1

Двоичная система счисления:

В двоичной системе счисления разрядные слагаемые чисел представляются в виде суммы произведений цифр на степени 2.

Число	Разрядные слагаемые
10	1 * 2 + 0 * 1
1101	1 * 8 + 1 * 4 + 0 * 2 + 1 * 1

Шестнадцатеричная система счисления:

В шестнадцатеричной системе счисления разрядные слагаемые чисел представляются в виде суммы произведений цифр на степени 16.

Число	Разрядные слагаемые
3F	3 * 16 + 15 * 1
7B8	7 * 256 + 11 * 16 + 8 * 1

Это лишь несколько примеров из множества возможных случаев использования разрядных слагаемых чисел в различных системах счисления. Их понимание может быть полезным для работы с числами в программировании, криптографии и других областях.

А что такое «диагональ»?

Обозначим вершины фигур буквами.

Соединим отрезком вершины прямоугольника из верхнего угла в нижний. Место пересечения отрезков тоже обозначим буквой.

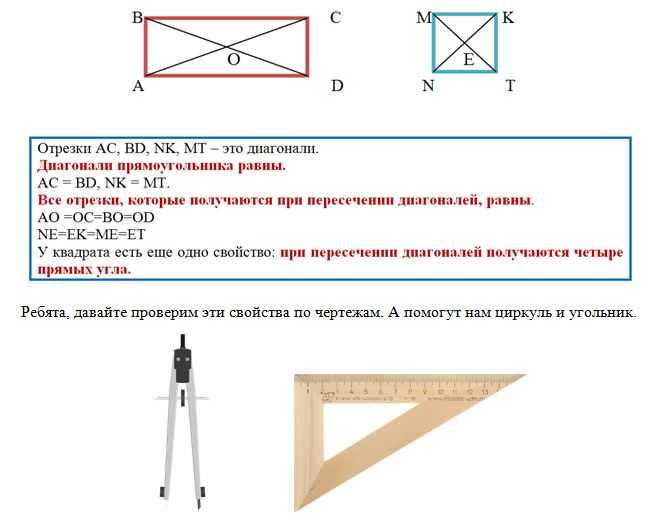
• Поставьте ножку циркуля в точку пересечения диагоналей и сравните по длине все отрезки, которые получились при пересечении.
• Длины диагоналей можно сравнить с помощью циркуля или измерить по линейке.
• А вот свойство квадрата о прямых углах, которые получаются при пересечении диагоналей, проверьте с помощью угольника. Вот так:

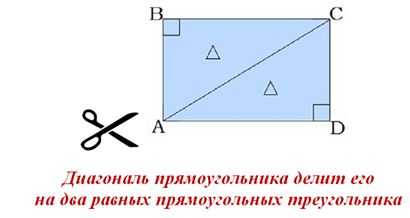
Ребята, вооружитесь ножницами! Проверим еще одно свойство прямоугольника. Вырежем из бумаги в клетку любой прямоугольник, согнем его из уголка в уголок и разрежем по линии сгиба (по диагонали). У нас получилось два треугольника. Наложите треугольники друг на друга. Сделайте вывод: равны ли треугольники? 

Определение, что такое разрядные слагаемые с примерами разряда и класса в математике

Главная > Наука > Математика > Разрядные слагаемые в математике

Число — это математическое понятие для количественного описания чего-либо или его части, служит также для сравнения целого и частей, расположения по порядку. Понятие числа изображается знаками или цифрами в различном сочетании. В настоящее время почти везде используются цифры от 1 до 9 и 0. Цифры в виде семи латинских букв применения почти не имеют и рассматриваться здесь не будут.

…

Мой мир

• Натуральные числа
• Разряды и классы чисел
• Разряды
• Классы

Натуральные числа

При счёте: «один, два, три… сорок четыре» или расстановке по очереди: «первый, второй, третий… сорок четвёртый» используются естественные числа, которые называются натуральными. Вся эта совокупность называется «ряд натуральных чисел» и обозначается латинской буквой N и не имеет конца, ведь всегда есть число ещё больше, и са́мого большого просто не существует.

Разряды

единиц

десятков

сотен

Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.

Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.

Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.

Классы

Первый — единиц, содержит до 3 знаков:

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.

Сорок пять состоит из четырёх десятков и пяти простых единиц.

Второй — тысяч, от 4 до 6 знаков:

679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

Эта сумма состоит из следующих разрядных слагаемых:

1. шестьсот тысяч;
2. семьдесят тысяч;
3. девять тысяч;
4. восемьсот;
5. десять;
6. два;

3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

Это число содержит девять разрядных слагаемых:

1. 800 миллионов;
2. 80 миллионов;
3. 7 миллионов;
4. 200 тысяч;
5. 10 тысяч;
6. 3 тысячи;
7. 6 сотен;
8. 4 десятка;
9. 4 единицы;

В этом числе нет слагаемых выше 7 разряда.

Четвёртый — миллиардов, от 10 до 12 цифр:

Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.

Разрядные слагаемые 4 класса читаются слева направо:

1. единицы сотен миллиардов;
2. единицы десятков миллиардов;
3. единицы миллиардов;
4. сотен миллионов;
5. десятков миллионов;
6. миллионов;
7. сотен тысяч;
8. десятков тысяч;
9. тысяч;
10. простые сотни;
11. простые десятки;
12. простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.

При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

Читается слева:

Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.

Шестой — квадриллионов, 16—18 цифр.

Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.

Седьмой — квинтиллионов, 19—21 знак.

771 642 962 921 398 634 389.

Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.

Восьмой — секстиллионов, 22—24 цифры.

842 527 342 458 752 468 359 173

Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.

Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.

Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31, чем приписывать тридцать один ноль к единице.