Числа за миллионом: как они называются и чем отличаются
После миллиона в таблице чисел следует числовой ряд, который начинается со слова «миллион». Однако, названия чисел за миллионом, частенько используются в различных академических и научных дисциплинах, и могут отличаться в зависимости от страны.
Наиболее распространенные названия чисел за миллионом — миллиард, триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион, дециллион.
Каждое последующее число является тысячекратным умножением предыдущего, так, миллиард — это тысяча миллионов, триллион — тысяча миллиардов и т.д.
Несмотря на то, что большинство из этих чисел мало используются в повседневной жизни, они широко применяются в экономических и финансовых сферах, криптографии, астрономии и математических науках в целом.
Для более наглядного представления можно привести таблицу с названиями чисел и их порядковыми номерами в ряду:
| Название числа | Порядковый номер |
|---|---|
| миллиард | 10^9 |
| триллион | 10^12 |
| квадриллион | 10^15 |
| квинтиллион | 10^18 |
| секстиллион | 10^21 |
| септиллион | 10^24 |
| октиллион | 10^27 |
| нониллион | 10^30 |
| дециллион | 10^33 |
использованная литература
- . Словарь американского наследия (4-е изд.). 2000 г. ISBN 0-395-82517-2.
- Оксфордский словарь английского языка, 2-е издание, Оксфорд, Великобритания: Oxford University Press. ISBN 0-19-861186-2 (и дополнения с момента публикации в 1989 г.)
- В Словарь случайных домов, 2-е полное издание, 1987, Random House.
- Краткий оксфордский словарь английского языка, 3-е издание, 1993 г., Oxford: Clarendon Press.
- Третий новый международный словарь Вебстера, Несокращенный, 1993, Merriam-Webster.
- п. 316, История английского языка, Оливер Фаррар Эмерсон, Нью-Йорк, Лондон: Macmillan and Co., 1894.
- Каснер, Эдвард и Джеймс Ньюман, Математика и воображение, 1940, Саймон и Шустер, Нью-Йорк.
- ^ Книга чисел, Дж. Х. Конвей и Р. К. Гай, Нью-Йорк: Springer-Verlag, 1996, стр. 15–16. ISBN 0-387-97993-X.
- Бауэрс, Джонатан. «Скребки бесконечности». Политоп, 2010.
Нули, сгруппированные в наборы по 3
Ссылка на наборы нулей зарезервирована для групп из трех нулей, что означает, что они не актуальны для меньших чисел. Мы пишем числа с запятыми, разделяющими наборы из трех нулей, чтобы было легче читать и понимать значение. Например, вы пишете один миллион как 1000000, а не как 1000000.
В качестве другого примера гораздо проще вспомнить, что триллион записывается с четырьмя наборами по три. нулей, чем для подсчета 12 отдельных нулей. Хотя вы можете подумать, что это довольно просто, просто подождите, пока вам не придется считать 27 нулей для октиллиона или 303 нуля для сантиллиона.
Это так. тогда вы будете благодарны за то, что вам нужно запомнить только девять и 101 набор нулей соответственно.
Римские цифры — генезис
Римские цифры (их часто ошибочно называют «латинскими») являются разработкой и достоянием Римской цивилизации. Древние римляне создали их для облегчения счёта, дабы проще и удобнее считать разнообразные товары и услуги.
Римские цифры широко использовались в ходе существования единого римского государства, а также после его раскола на Западную и Восточную Римскую Империю. Даже после падения Константинополя они продолжали использоваться в различных варварских королевствах вплоть до конца Средневековья, пока постепенно не проиграли соперничество арабо-индийским цифрам, доминирующим по сей день.

Концепция числовой последовательности
Числовая последовательность — это упорядоченный набор чисел, расположенных в определенном порядке. Каждый элемент последовательности обозначается символом an, где n — порядковый номер элемента.
Таким образом, числовая последовательность может быть представлена в виде a1,a2,a3,…,an,…, где a1 — первый элемент, a2 — второй элемент и так далее.
Существует множество типов числовых последовательностей: арифметические, геометрические, рекуррентные и др. Арифметическая последовательность представляет собой последовательность, в которой каждый следующий элемент отличается от предыдущего на постоянную величину, называемую разностью. Геометрическая последовательность — это последовательность, в которой каждый следующий элемент отличается от предыдущего в постоянное число раз, называемое знаменателем.
Важным понятием в теории числовых последовательностей является предел последовательности. Предел последовательности — это число, к которому стремятся элементы последовательности по мере увеличения номера. Если предел последовательности существует и конечен, то говорят, что последовательность сходится. Если предел не существует или бесконечен, то говорят, что последовательность расходится.
Числовые последовательности находят свое применение во многих областях математики и естественных наук. Они используются при решении уравнений, ряда задач на физику, экономику, криптографию и т.д.
Римские цифры — генезис
Римские цифры (их часто ошибочно называют «латинскими») являются разработкой и достоянием Римской цивилизации. Древние римляне создали их для облегчения счёта, дабы проще и удобнее считать разнообразные товары и услуги.
Римские цифры широко использовались в ходе существования единого римского государства, а также после его раскола на Западную и Восточную Римскую Империю. Даже после падения Константинополя они продолжали использоваться в различных варварских королевствах вплоть до конца Средневековья, пока постепенно не проиграли соперничество арабо-индийским цифрам, доминирующим по сей день.

Разряды чисел
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Разряд числа — это позиция (место) цифры в записи числа.
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
- Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
- Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
- Сотни — единицами третьего разряда и пишутся на третьем месте справа.
- Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
- Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Решение:
1) 37 565;
2) 450 009;
3) 8 050.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
и так далее.
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
20 507 — двадцать тысяч пятьсот семь.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Названия больших чисел
Для удобства чтения и запоминания больших чисел цифры их разбивают на так называемые «классы»: справа отделяют три цифры (первый класс), затем еще три (второй класс) и т.д. Последний класс может иметь три, две и одну цифру. Между классами обычно оставляется небольшой пробел. Например, число 35461298 записывают так 35 461 298 . Здесь 298 — первый класс, 461 — второй класс, 35 — третий. Каждая из цифр класса называется его разрядом; счет разрядов также идет справа. Например, в первом классе 298 цифра 8 составляет первый разряд, 9 — второй, 2 — третий. В последнем классе может быть три, два разряда (в нашем примере: 5 — первый разряд, 3 — второй) или один.
Первый класс дает число единиц, второй — тысяч, третий — миллионов; сообразно с этим число 35 461 298 читается: тридцать пять миллионов четыреста шестьдесят одна тысяча двести девяносто восемь. Поэтому говорят, что единица второго класса есть тысяча; единица третьего класса — миллион.
Таблица, Названия больших чисел
| 1 = 10 0 | один |
| 10 = 10 1 | десять |
| 100 = 10 2 | сто |
| 1 000 = 10 3 | тысяча |
| 10 000 = 10 4 | |
| 100 000 = 10 5 | |
| 1 000 000 = 10 6 | миллион |
| 10 000 000 = 10 7 | |
| 100 000 000 = 10 8 | |
| 1 000 000 000 = 10 9 | миллиард(биллион) |
| 10 000 000 000 = 10 10 | |
| 100 000 000 000 = 10 11 | |
| 1 000 000 000 000 = 10 12 | триллион |
| 10 000 000 000 000 = 10 13 | |
| 100 000 000 000 000 = 10 14 | |
| 1 000 000 000 000 000 = 10 15 | квадриллион |
| 10 000 000 000 000 000 = 10 16 | |
| 100 000 000 000 000 000 = 10 17 | |
| 1 000 000 000 000 000 000 = 10 18 | квинтиллион |
| 10 000 000 000 000 000 000 = 10 19 | |
| 100 000 000 000 000 000 000 = 10 20 | |
| 1 000 000 000 000 000 000 000 = 10 21 | секстиллион |
| 10 000 000 000 000 000 000 000 = 10 22 | |
| 100 000 000 000 000 000 000 000 = 10 23 | |
| 1 000 000 000 000 000 000 000 000 = 10 24 | сеплиллион |
| 10 000 000 000 000 000 000 000 000 = 10 25 | |
| 100 000 000 000 000 000 000 000 000 = 10 26 | |
| 1 000 000 000 000 000 000 000 000 000 = 10 27 | октиллион |
| 10 000 000 000 000 000 000 000 000 000 = 10 28 | |
| 100 000 000 000 000 000 000 000 000 000 = 10 29 | |
| 1 000 000 000 000 000 000 000 000 000 000 = 10 30 | нониллион |
| 10 000 000 000 000 000 000 000 000 000 000 = 10 31 | |
| 100 000 000 000 000 000 000 000 000 000 000 = 10 32 | |
| 1 000 000 000 000 000 000 000 000 000 000 000 = 10 33 | дециллион |
Единица четвертого класса называется миллиардом, или, иначе, биллионом ( 1 миллиард = 1000 миллионов).
Единица пятого класса называется триллионом ( 1 триллион = 1000 биллионов или 1000 миллиардов).
Единицы шестого, седьмого, восьмого и т.д. классов (каждая из которых в 1000 раз больше предшествующей) называются квадриллионом, квинтиллионом, секстиллионом, септиллионом и т.д.
Пример: 12 021 306 200 000 читается: двенадцать триллионов двадцать один миллиард триста шесть миллионов двести тысяч.
Многозначные числа.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.Трехзначные числа состоят из трех цифр, например: 354, 444, 780.Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Сколько нулей в числе Гуголплекс?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 апреля 2021 года; проверки требуют 38 правок, Гуголплекс (от англ. googolplex ) — число, равное степень 10 гугол (десяти в степени гугол ), то есть 10 10 100,
В десятичной записи число можно представить как одна единица и гугол нулей после неё. Как и гугол, термин «гуголплекс» был придуман американским математиком Эдвардом Казнером ( англ. Edward Kasner ) и его племянником Милтоном Сироттой ( англ. Milton Sirotta ), Число гугол (а тем более, гуголплекс) больше числа всех частиц в известной нам части вселенной, которое составляет величину от 10 79 до 10 81,
Факториал гугола больше гуголплекса: 10 100 ! = 10 9,9565705518×10 101
Использование названий больших чисел
Некоторые названия больших чисел, например миллион, миллиард, и триллион, имеют реальные ссылки в человеческом опыте и встречаются во многих контекстах. Иногда названия больших чисел были вынуждены стать общеупотребительными в результате гиперинфляция. Банкнота с самой высокой числовой стоимостью из когда-либо напечатанных была купюрой в 1 секстиллион. Peng (1021 или 1 миллиард миллиардов фунтов стерлингов, как напечатано) Венгрия в 1946 г. В 2009 г. Зимбабве напечатал 100 триллионов (1014) Зимбабвийский доллар примечание, которое на момент печати стоило около 30 долларов США.
Имена больших чисел, однако, существуют ненадолго, искусственно, редко встречаются вне определений, списков и обсуждений способов именования больших чисел. Даже такие известные имена, как секстиллион используются редко, поскольку в контексте науки, включая астрономию, где часто встречаются такие большие числа, они почти всегда записываются с использованием научная нотация. В этих обозначениях степени десяти выражаются как 10 с числовым надстрочным индексом, например «Рентгеновское излучение радиогалактики составляет 1.3×1045 джоули. «Когда такое число, как 1045 необходимо передать словами, это просто читается как «от десяти до сорок пятого». Это легче сказать и менее двусмысленно, чем «quattuordecillion», что означает нечто иное в длинной и короткой шкалах.
Когда число представляет собой количество, а не количество, Префиксы SI может использоваться — таким образом, «фемтосекунда», а не «одна квадриллионная секунды» — хотя часто вместо некоторых очень высоких и очень низких префиксов используются степени десяти. В некоторых случаях используются специализированные устройства, например, астрономический парсек и световой год или физика элементарных частиц сарай.
Тем не менее, большие числа обладают интеллектуальным увлечением и представляют математический интерес, и присвоение им имен — один из способов, с помощью которых люди пытаются осмыслить и понять их.
Один из самых ранних примеров этого — Счетчик песка, в котором Архимед дал систему именования больших чисел. Для этого он набрал номера до мириады мириады (108) «первые номера» и набрал 108 Сама «единица вторых чисел». Затем кратные этой единицы стали вторыми числами, до этой единицы принималось мириады раз, 108·108=1016. Это стало «единицей третьих чисел», кратными третьим числам и так далее. Архимед продолжал называть числа таким образом до бесчисленного множества раз больше единицы из десяти.8-е числа, т.е. (108)(108)=108⋅108,{ displaystyle (10 ^ {8}) ^ {(10 ^ {8})} = 10 ^ {8 cdot 10 ^ {8}},} и встроил эту конструкцию в другую свою копию, чтобы получить имена для чисел до ((108)(108))(108)=108⋅1016.{ displaystyle ((10 ^ {8}) ^ {(10 ^ {8})}) ^ {(10 ^ {8})} = 10 ^ {8 cdot 10 ^ {16}}.} Затем Архимед оценил количество песчинок, которое потребуется, чтобы заполнить известную вселенную, и обнаружил, что это не более «тысячи мириад восьмых чисел» (1063).
С тех пор многие другие занимались концептуализацией и именованием чисел, которые действительно не существуют вне воображения. Одна из причин такого стремления заключается в том, что изобретатель слова гугол, который был уверен, что любое конечное число «должно иметь имя». Еще одна возможная мотивация — это соревнование между студентами курсов компьютерного программирования, где обычным упражнением является написание программы для вывода чисел в форме английских слов.
Большинство названий, предлагаемых для больших чисел, относятся к систематическим схемам, которые можно расширять. Таким образом, многие имена для больших чисел являются просто результатом следования системе именования до ее логического завершения или дальнейшего ее расширения.
Имена для больших чисел часто используются в инкрементальные игры, также известные как холостые игры.
Представление римских цифр от 1 до 1000
Римские цифры представлены семью различными буквами — I, V, X, L, C, D и M, каждая из которых обозначает какое-либо число.
Запомнить римские цифры от 1 до 1000 можно с помощью следующего словосочетания (в порядке убывания):
Указанные семь букв используются для представления множества различных чисел, обычно с помощью суммирования. К примеру, римское число 2 пишется как «II» (просто две единички добавленные вместе). Число 12 – как XII, то есть X+II. Ну а номер 27 пишется как XXVII, то есть как сочетание XX + V + II.
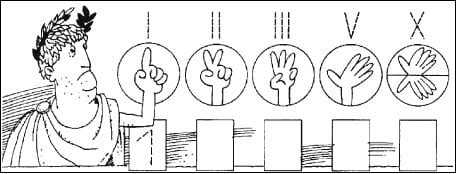
Римские цифры удобно отображались пальцами
Как видим, римские цифры записываются начиная от самой большой цифры и заканчивая маленькой, слева направо. Однако, это ещё не всё. Римляне очень не любили 4 однотипных цифры в ряду, поэтому они разработали специальную систему вычитания.
В римских цифрах число 3 пишется как «III». Однако, цифра для числа 4 будет не «IIII», так как здесь находятся четыре однотипных символа, и необходимо использовать принцип вычета. Римскими цифрами число 4 будет записываться как «IV», то есть номера 1 и 5. Поскольку меньшая цифра (1) стоит перед большей (5), то мы из большей цифры вычитываем меньшую, и получаем 4. Тот же принцип используется в отношении номера «9», который в римской системе записывается как «IX» (1 и 10)
Вот ещё шесть аналогичных примеров, позволяющих использовать римские цифры от 1 до 1000:
- I может стоять раньше V (5) и X (10) создавая числа 4 и 9.
- X может стоять раньше чем L (50) и C (100) создавая числа 40 и 90.
- C может стоять раньше D (500) и M (1000) создавая числа 400 и 900.
Номер 1994 является отличным примером для данного правила. В римских цифрах оно выглядит как MCMXCIV, то есть M = 1000, CM = 900, XC = 90 и IV = 4.
Таблица, Названия больших чисел
| 1 = 100 | один |
| 10 = 101 | десять |
| 100 = 102 | сто |
| 1 000 = 103 | тысяча |
| 10 000 = 104 | |
| 100 000 = 105 | |
| 1 000 000 = 106 | миллион |
| 10 000 000 = 107 | |
| 100 000 000 = 108 | |
| 1 000 000 000 = 109 | миллиард(биллион) |
| 10 000 000 000 = 1010 | |
| 100 000 000 000 = 1011 | |
| 1 000 000 000 000 = 1012 | триллион |
| 10 000 000 000 000 = 1013 | |
| 100 000 000 000 000 = 1014 | |
| 1 000 000 000 000 000 = 1015 | квадриллион |
| 10 000 000 000 000 000 = 1016 | |
| 100 000 000 000 000 000 = 1017 | |
| 1 000 000 000 000 000 000 = 1018 | квинтиллион |
| 10 000 000 000 000 000 000 = 1019 | |
| 100 000 000 000 000 000 000 = 1020 | |
| 1 000 000 000 000 000 000 000 = 1021 | секстиллион |
| 10 000 000 000 000 000 000 000 = 1022 | |
| 100 000 000 000 000 000 000 000 = 1023 | |
| 1 000 000 000 000 000 000 000 000 = 1024 | сеплиллион |
| 10 000 000 000 000 000 000 000 000 = 1025 | |
| 100 000 000 000 000 000 000 000 000 = 1026 | |
| 1 000 000 000 000 000 000 000 000 000 = 1027 | октиллион |
| 10 000 000 000 000 000 000 000 000 000 = 1028 | |
| 100 000 000 000 000 000 000 000 000 000 = 1029 | |
| 1 000 000 000 000 000 000 000 000 000 000 = 1030 | нониллион |
| 10 000 000 000 000 000 000 000 000 000 000 = 1031 | |
| 100 000 000 000 000 000 000 000 000 000 000 = 1032 | |
| 1 000 000 000 000 000 000 000 000 000 000 000 = 1033 | дециллион |
Единица четвертого класса называется миллиардом, или, иначе, биллионом (1 миллиард = 1000 миллионов).
Единица пятого класса называется триллионом (1 триллион = 1000 биллионов или 1000 миллиардов).
Единицы шестого, седьмого, восьмого и т.д. классов (каждая из которых в 1000 раз больше предшествующей) называются квадриллионом, квинтиллионом, секстиллионом, септиллионом и т.д.
| стр. 9 |
Семья гугол
Имена гугол и гуголплекс были изобретены Эдвард Каснер племянника Милтона Сиротты, представленного в книге Каснера и Ньюмана 1940 г. Математика и воображениев следующем отрывке:
| Ценность | имя | Орган власти |
|---|---|---|
| 10100 | Гугол | Каснер и Ньюман, словари (см. Выше) |
| 10гугол = 1010100 | Гуголплекс | Каснер и Ньюман, словари (см. Выше) |
Джон Хортон Конвей и Ричард К. Гай предположили, что N-plex использоваться как имя для 10N. Отсюда и название гуголкомплекс на 10гуголплекс = 101010100. Это число (десять в степени гуголплекса) также известно как гуголдуплекс и гуголплекс. Конвей и Гай предложили, что N-minex использоваться как имя для 10−N, дав начало имени гуголминекс для взаимный гуголплекса. Ни одно из этих имен не широко используется и в настоящее время не встречается в словарях.
Имена гугол и гуголплекс вдохновил название Интернет-компания и это Штаб-квартира компании, то Googleplex соответственно.
Сравнение систем
Таблица от значения к названию
| Порядок | Значение | Короткая шкала | Длинная шкала | СИ | ||
|---|---|---|---|---|---|---|
| Название | Логика построения | Название | Логика построения | |||
| 10 | один | один | ||||
| 1 | 103 | тысяча | 10001 + 0 | тысяча | 1 000 0000,5 | кило |
| 2 | 106 | миллион | 10001 + 1 | миллион | 1 000 0001,0 | мега |
| 3 | 109 | биллион (рус: миллиард) | 10001 + 2 | тысяча миллионов (миллиард) | 1 000 0001,5 | гига |
| 4 | 1012 | триллион | 10001 + 3 | биллион | 1 000 0002,0 | тера |
| 5 | 1015 | квадриллион | 10001 + 4 | тысяча биллионов (биллиард) | 1 000 0002,5 | пета |
| 6 | 1018 | квинтиллион | 10001 + 5 | триллион | 1 000 0003,0 | экса |
| 7 | 1021 | секстиллион | 10001 + 6 | тысяча триллионов (триллиард) | 1 000 0003,5 | зетта |
| 8 | 1024 | септиллион | 10001 + 7 | квадриллион | 1 000 0004,0 | йотта |
| 9 | 1027 | октиллион | 10001 + 8 | квадриллиард | 1 000 0004,5 | мутта |
| 10 | 1030 | нониллион | 10001 + 9 | квинтиллион | 1 000 0005,0 | пепта |
| 11 | 1033 | дециллион | 10001 + 10 | квинтиллиард | 1 000 0005,5 | уно |
Жилой фонд России и четыре футбольных поля как примеры
На каждого человека на земле приходится площадь суши размером 100х200 метров. Это примерно четыре футбольных поля. Но если людей будет не 7 миллиардов, а семь триллионов, то каждому достанется только кусочек суши 4х5 метров. Четыре футбольных поля против площади палисадника перед подъездом – таково соотношение миллиарда к триллиону.
В абсолютных значениях картина также впечатляет.
Если взять триллион кирпичей, то можно построить более 30 миллионов одноэтажных домов площадью по 100 квадратных метров. То есть около 3 миллиардов квадратных метров частной застройки. Это сопоставимо с общим жилым фондом РФ.
Если строить десятиэтажные дома, то получится примерно 2,5 миллиона домов, то есть 100 миллионов двух- трехкомнатных квартир, около 7 миллиардов квадратных метров жилья. Это в 2,5 раза больше всего жилого фонда России.
Одним словом, во всей России не наберется триллион кирпичей.
Жилой фонд России и четыре футбольных поля как примеры
На каждого человека на земле приходится площадь суши размером 100х200 метров. Это примерно четыре футбольных поля. Но если людей будет не 7 миллиардов, а семь триллионов, то каждому достанется только кусочек суши 4х5 метров. Четыре футбольных поля против площади палисадника перед подъездом – таково соотношение миллиарда к триллиону.
В абсолютных значениях картина также впечатляет.
Если взять триллион кирпичей, то можно построить более 30 миллионов одноэтажных домов площадью по 100 квадратных метров. То есть около 3 миллиардов квадратных метров частной застройки. Это сопоставимо с общим жилым фондом РФ.
Если строить десятиэтажные дома, то получится примерно 2,5 миллиона домов, то есть 100 миллионов двух- трехкомнатных квартир, около 7 миллиардов квадратных метров жилья. Это в 2,5 раза больше всего жилого фонда России.
Одним словом, во всей России не наберется триллион кирпичей.
Один квадриллион ученических тетрадей покроет всю территорию России двойным слоем. А один квинтиллион тех же тетрадей накроет всю сушу слоем толщиной в 40 сантиметров. Если же удастся раздобыть секстиллион тетрадей, то вся планета, включая океаны, окажется под слоем толщиной в 100 метров.
Представление римских цифр от 1 до 1000
Римские цифры представлены семью различными буквами — I, V, X, L, C, D и M, каждая из которых обозначает какое-либо число.
Запомнить римские цифры от 1 до 1000 можно с помощью следующего словосочетания (в порядке убывания):
Указанные семь букв используются для представления множества различных чисел, обычно с помощью суммирования. К примеру, римское число 2 пишется как «II» (просто две единички добавленные вместе). Число 12 – как XII, то есть X+II. Ну а номер 27 пишется как XXVII, то есть как сочетание XX + V + II.

Римские цифры удобно отображались пальцами
Как видим, римские цифры записываются начиная от самой большой цифры и заканчивая маленькой, слева направо. Однако, это ещё не всё. Римляне очень не любили 4 однотипных цифры в ряду, поэтому они разработали специальную систему вычитания.
В римских цифрах число 3 пишется как «III». Однако, цифра для числа 4 будет не «IIII», так как здесь находятся четыре однотипных символа, и необходимо использовать принцип вычета. Римскими цифрами число 4 будет записываться как «IV», то есть номера 1 и 5. Поскольку меньшая цифра (1) стоит перед большей (5), то мы из большей цифры вычитываем меньшую, и получаем 4. Тот же принцип используется в отношении номера «9», который в римской системе записывается как «IX» (1 и 10)
Вот ещё шесть аналогичных примеров, позволяющих использовать римские цифры от 1 до 1000:
- I может стоять раньше V (5) и X (10) создавая числа 4 и 9.
- X может стоять раньше чем L (50) и C (100) создавая числа 40 и 90.
- C может стоять раньше D (500) и M (1000) создавая числа 400 и 900.
Номер 1994 является отличным примером для данного правила. В римских цифрах оно выглядит как MCMXCIV, то есть M = 1000, CM = 900, XC = 90 и IV = 4.
Короткая шкала
В случае короткой шкалы все названия больших чисел строятся так: в начале идёт латинское порядковое числительное, а в конце к нему добавляется суффикс «-иллион». Исключение составляет название «миллион», которое является названием числа тысяча (лат. mille) и увеличительного суффикса «-иллион». Так получаются числа — биллион, триллион, квадриллион, квинтиллион, секстиллион и т. д. Система наименования чисел с короткой шкалой используется в России, США, Канаде, Великобритании, Греции и Турции. Количество нулей в числе, записанном по этой системе, определяется по формуле 3·x+3 (где x — латинское числительное).
В , в том числе и в России, вместо слова «биллион» используется слово «миллиард».
Что больше Триллиарда?
Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион. А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Число Пи — одно из самых таинственных Американская – довольно простая. Названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион, что значит тысяча. Далее получаются числа: триллион, квадриллион, квинтиллион, секстиллион, септиллион, октиллион, нониллион и дециллион.
То есть после триллиона идет триллиард, после квадриллион, квадриллиард и так далее. Получается, что по английской и американской системам одни и те же большие числа называются по-разному. В русский язык из английской системы пришел только миллиард (10 9), который американцы называют биллионом. Нас окружают миллионы чисел Кроме чисел, которые записаны при помощи английской или американской систем, известны так называемые внесистемные числа. То есть те, у которых есть свои собственные названия, в них нет латинских префиксов. Их несколько, вернемся к ним чуть позже.
А что же дальше? На самом деле можно с помощью приставок и дальше рождать числа-монстры: андециллион, дуодециллион, тредециллион и так далее. Но нам нужны собственные названия чисел, а тут только составные названия.
Что выше триллиона?
Короткая шкала — В случае короткой шкалы все названия больших чисел строятся так: в начале слова ставится латинское числительное, обозначающее степень, которая добавляется к первой степени тысячи, затем к числительному добавляется суффикс «-иллион», вычлененный из слова «миллион», где «милли» — от латинского числительного mille — тысяча (а не степень, добавляемая к первой степени тысячи), а «-он» ( -one ) — увеличительный суффикс, который добавляет 1 к первой степени тысячи.
Именованные большие числа с короткой шкалой (в скобках указаны степени тысячи): миллион (2), биллион (3), триллион (4), квадриллион (5), квинтиллион (6), секстиллион (7) и т.д. Система наименования чисел с короткой шкалой используется в России и других странах бывшего СССР, англоязычном и арабоязычном мире, Бразилии, Болгарии, Греции, Румынии и Турции,
При этом вместо слова «биллион» обычно используется слово « миллиард », за исключением англоязычного мира и Бразилии. Количество нулей числа с короткой шкалой определяется по формуле 3·(n+1), где n 1 — степень из названия числа, добавляемая к первой степени тысячи.
Какое самое большое число в мире?
Не следует путать с Google, Гуго́л (от англ. googol ) — число, в десятичной системе счисления изображаемое единицей со 100 нулями: 10 100 = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
Как называется число с 22 нулями?
Литература —
Квадриллион // Большая советская энциклопедия : / гл. ред.А.М. Прохоров, — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
| Это «статья-заготовка» по математике, Вы можете помочь проекту, дополнив эту статью, как и любую другую в Википедии. Нажмите и узнайте подробности, |
table>
Числа с собственными именами
Математические константы
| Алгебраические |
|
|---|---|
| Трансцендентные, вероятно трансцендентные |
|
/td>
Степени тысячи
- Тысяча
- Миллион
- Миллиард
- Биллион
- Триллион
- Квадриллион
- Квинтиллион
- ,, другие
Древнерусские числа
- Тьма
- Легион (неведий)
- Леодр
- Вран (ворон)
- Колода
- Тьма тем
Прочие степени десяти
- Мириада
- Лакх
- Крор
- Аравб
- Гугол
- Асанкхейя
- Гуголплекс
Степени двенадцати
- Дюжина
- Гросс
- Масса
Прочие целые
- 1
- Константа Лежандра
- Чёртова дюжина
- 40
- Число зверя
- Число Рамануджана — Харди
- Число Авогадро
- Число Скьюза
- Число Мозера
- Число Грэма
- Число Райо
Прочие числа
Источник — https://ru.
Заключение
Спецификация римских цифр предполагает использование всего семи букв, обозначающих круглые цифры от 1 до 1000. Несмотря на прежнее широкое распространение, принципы сложения и вычитания таких цифр несут для считающего ряд неудобств, вследствие чего система римских цифр проиграла конкуренцию более совершенной арабской модели
Тем не менее мы можем встретить римские цифры в спортивной, военной, научной и иных сферах, потому важно знать особенности их отображения и применения
В школьные годы многие девочки-подростки впервые знакомятся с таинственным миром непознанного. И знакомство это происходит чаще всего посредством различных гаданий. К примеру, одним из самых популярных видов ворожбы является гадание на цифрах.






























