§ разряды и классы. класс единиц, тысяч и миллионов

Многозначные числа.

Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.Трехзначные числа состоят из трех цифр, например: 354, 444, 780.Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.

Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.

Примеры решения задач

Для чего требуется знание числовых разрядов на практике? Для правильного нахождения суммы и разности чисел.

Хотя подобные примеры можно решить онлайн, полезнее уметь просчитывать их самостоятельно. Вычисления проводятся при помощи сложения или вычитания в столбик или

Задача 1

Найти сумму 135 и 241.

Для этого требуется сложить 135 и 241. При этом единицы складываются с единицами и так далее. Поэтому сначала нужно охарактеризовать позицию цифр каждого из слагаемых.

Далее производится сложение – 135 + 241:

друг к другу прибавляются единицы – 1 + 5 = 6;
складываются десятки – 3 + 4 = 7;
складываются сотни – 1 + 2 = 3.

+	1	3	5
2	4	1
	3	7	6

Ответ: 376.

Сходным образом выполняется вычитание.

Задача 2

Найти разность 567 и 254:

сначала вычитаются значения единиц 7 – 4 = 3;
отнимают десятки 6 – 5 = 1;
вычитают сотни 5 – 2 = 3.

–	5	6	7
2	5	4
	3	1	3

Ответ: 313.

АлгебраФакториал определение, формула, обозначение, основные свойства и функции, таблица, алгоритмы нахождения, примеры задач с решениями, онлайн-калькулятор
Следующая
АлгебраЭквивалентные функции определение, формулы, основные свойства, доказательство теоремы о замене функций, примеры нахождения пределов, таблица

Предыдущая
АлгебраФакториал определение, формула, обозначение, основные свойства и функции, таблица, алгоритмы нахождения, примеры задач с решениями, онлайн-калькулятор
Следующая
АлгебраЭквивалентные функции определение, формулы, основные свойства, доказательство теоремы о замене функций, примеры нахождения пределов, таблица

Правило встречается в следующих упражнениях:

2 класс

Страница 41. Урок 21,
Петерсон, Учебник, часть 1

Страница 42. Урок 22,
Петерсон, Учебник, часть 1

Страница 43. Урок 22,
Петерсон, Учебник, часть 1

Страница 48. Урок 25,
Петерсон, Учебник, часть 1

Страница 65. Урок 33,
Петерсон, Учебник, часть 1

Страница 35. Урок 12,
Петерсон, Учебник, часть 3

3 класс

Страница 41. Урок 15,
Петерсон, Учебник, часть 1

Страница 68. Урок 23,
Петерсон, Учебник, часть 1

Страница 87. Урок 32,
Петерсон, Учебник, часть 1

Страница 93. Урок 35,
Петерсон, Учебник, часть 1

Страница 6. Урок 3,
Петерсон, Учебник, часть 2

Страница 14. Урок 6,
Петерсон, Учебник, часть 2

Страница 38. Урок 15,
Петерсон, Учебник, часть 2

Страница 48. Урок 19,
Петерсон, Учебник, часть 2

Страница 56. Урок 23,
Петерсон, Учебник, часть 2

Страница 37. Урок 17,
Петерсон, Учебник, часть 3

4 класс

Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 17. ПР 1. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 77. Тест. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 80. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 27,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 78. Урок 26,
Петерсон, Учебник, часть 1

5 класс

Задание 1156,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 562,
Мерзляк, Полонский, Якир, Учебник

Номер 846,
Мерзляк, Полонский, Якир, Учебник

Номер 847,
Мерзляк, Полонский, Якир, Учебник

Номер 851,
Мерзляк, Полонский, Якир, Учебник

Номер 852,
Мерзляк, Полонский, Якир, Учебник

Номер 853,
Мерзляк, Полонский, Якир, Учебник

Номер 854,
Мерзляк, Полонский, Якир, Учебник

Номер 857,
Мерзляк, Полонский, Якир, Учебник

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Операция умножения и деления

Операция умножения — это комбинация двух чисел, произведение которых является новым числом. Знаком умножения является знаком «×». Например, 3 × 4 = 12, где 3 и 4 являются множителями, а 12 является произведением.

Правила умножения:

Умножать можно любые числа
Множители можно менять местами, результат не изменится: 4 × 3 = 3 × 4
Произведение чисел не зависит от порядка умножения: 3 × 4 = 12, 4 × 3 = 12, 12 ÷ 3 = 4, 12 ÷ 4 = 3
Умножение числа на 1 не изменяет его: 5 × 1 = 5
Умножение числа на 0 дает результат равный 0: 5 × 0 = 0

Операция деления — это нахождение количества одинаковых частей, на которые можно разделить число. Знак деления является знаком «÷». Например, 12 ÷ 3 = 4, где 12 является делимым, а 3 является делителем.

Правила деления:

Делить можно любые числа
При делении на 1 результат будет равен делимому: 5 ÷ 1 = 5
На 0 делить нельзя: 5 ÷ 0 = ошибка
В результате деления могут получаться дроби, но при делении одного целого числа на другое целое число результат может быть целым числом, целочисленным остатком или дробным числом.

Нумерация в математике 4 класс — это знакомство с основными арифметическими операциями, в том числе с умножением и делением. Понимание особенностей данных операций позволит ребенку освоить материал более глубоко и уверенно применять их в решении различных задач.

Задание 2

Запишите цифрами числа:

1. Сто восемь тысяч триста девять

2. Тридцать тысяч семьсот девять

3. Восемь тысяч шестьсот

Решение

Многозначные числа записывают по классам, начиная с высшего. Чтобы записать цифрами число, например «сто восемь тысяч триста девять», сначала записывают, сколько всего единиц второго, высшего, класса в числе – 108, потом записывают, сколько всего единиц первого класса в числе.

Для числа «тридцать тысяч семьсот семьдесят» запишем количество единиц второго высшего класса в числе, их тридцать, и количество единиц первого класса в числе, семьсот семьдесят.

В числе «восемь тысяч шестьсот» 8 единиц второго класса и шестьсот единиц первого класса.

2 класс – класс тысяч	1 класс – класс единиц
Сотни тысяч	Десятки тысяч	Единицы тысяч	Сотни	Десятки	Единицы
1	8	3	9
	3	7	7
		8	6

Математическая практика второго класса (я знаю)

О нас

Цены

Разрядное значение (до 99)

Чтение и запись чисел (до 99)

Разрядное значение (до 999)

Чтение и запись чисел (до 999)

Разрядное значение (до 9999)

Сравнение чисел с числом 99

Сравнение чисел с числом 999

Сравнение чисел с числом 9999

До, После, Между (до 100)

До, После, Между (до 1000)

Номера для заказа До 99

Номера для заказа До 999

Номера для заказа До 9999

Десять (до 99)

Нечетные и четные числа

Порядковые числа

Образцы чисел

Пропуск счета 2, 5 и 10 (базовый)

Пропуск счета 2, 5 и 10 Пропустить счет десятками и сотнями (базовый)

Счета пропуска на 10S и 100S (Advanced)

Подсчет пропуска на 25S

Добавить 10 к любому числу

Добавить 10 или 100 к любому числу

Очистки в таблицах

Дличие факты.

Сложение в любом порядке (переместительное свойство)

Сложение трех однозначных чисел (ассоциативное свойство)

Базовое вычитание в пределах 20

Факты вычитания Детализация в пределах 20

Сложение и вычитание в пределах 20

Факты сложения и вычитания Упражнение в пределах 20

Семейства фактов (до 20)

Пропущенные числа до 20 (сложение и вычитание)

Сложение двух цифр плюс 1 цифра

Что такое классы и разряды в математике?

В многозначных числах при записи цифры как бы разбивают на группы справа налево по три цифры в одну группу. Вот как раз таки эти самые группы и называются классами.

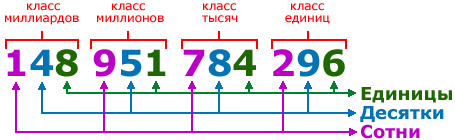
При записи многозначного числа на письме каждой цифре отводится определённое место — позиция. И вот это самое место, занимаемое конкретной цифрой носит название разряд.

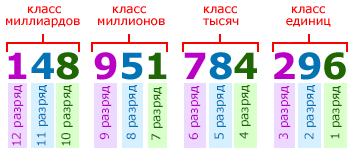
Всем нам, наверное, известно (даже гуманитарию), что в математике есть классы и разряды. К разрядам относятся:

1 разряд — единицы;

2 разряд — десятки;

3 разряд — сотни.

А вот к классам относятся единицы, тысячи, миллионы, миллиарды и так далее.

Вот таблица классов и разрядов для наглядности, чтобы было понятнее:

Чтобы было проще понять, нужно взять для примера некое число. Пусть это будет 38 593 501.

Цифры в записи любого натурального числа справа налево можно разделить в том порядке, в котором они стоят, на группы по 3 цифры в каждой группе. В последней группе может оказаться меньше трёх цифр, можно считать, что в недостающих позициях стоят нули, то есть ничего.

Каждая такая группа — это класс. Названия у классов определяются по порядку: единицы, тысячи, миллионы и т.д.

501 — класс единиц;

593 — класс тысяч;

38 — класс миллионов.

Разряд — позиция каждой цифры. Условно их можно пронумеровать (справа налево).

1 — первый разряд;

0 — второй разряд;

Также разряды можно назвать. В каждом отдельном классе первая цифра (справа налево) будет единицей, вторая — десятком, третья — сотней. Начиная, с класса тысяч перед «единица», «десяток», «сотня» добавляют название класса ( иногда вместо «единица» пишут название класса).

3 — единицы тысяч (тысячи);

9 — десятки тысяч;

8 — единицы миллионов (миллионы);

3 — десятки миллионов.

Вроде звучит сложно, но на самом деле просто все. Ребенок, изучая математику, а вместе с ней самые разные числа — и малые, и большие, понимает идею систематизации на основе классов и разрядов даже на интуитивном уровне.

Классы — понятие более крупное, оно стоит над разрядами, то есть включает их в себя. Классы бывают такого толка:

класс единиц: это все числа до 999;
класс тысяч: это все числа до 999 999;
класс миллионов: числа от 1 000 000 и далее.

Вы могли обратить внимание, что в каждом последующем классе происходит добавление на три позиции для чисел, а точнее, на новую тройку разрядов: если мы говорим о классе единиц, то там есть самый малый разряд — единицы, за ними следует разряд десятков, и, наконец, разряд сотен. В классе тысяч там уже такие разряды: тысячи, десятки тысяч, сотни тысяч

В классе миллионов тройка такая: миллионы, десятки миллионов, сотни миллионов. Помню, в школе нас поначалу специально заставляли ставить пробелы между этими тройками, чтобы было нагляднее и понятнее.

Обратите внимание: если значение какого-то разряда отсутствует, мы его не пропускаем при записи числа, но пишем ноль. Например, дан класс единиц, где разряд единиц — это 8, разряд десятков — это 0, разряд сотен — 2

Это будет число 208 (запись производится справа налево).

Сложение и вычитание в пределах 100. Устные и письменные приемы

Мой третий секрет: «Считайте быстро, используя разные приемы».

Переставляйте, где удобно, слагаемые или заменяйте соседние слагаемые их суммой.

Складывать и вычитать можно по разрядам.

Например, 16+38+27=(10+30+20)+(6+8+7)=60+21=81.

67-36=(60-30)+(7-6)=30+1=31

Складывать и вычитать двузначные числа можно по частям.

Попробуйте вычислить, пользуясь моим секретом:

76+9+4

47+6+14

50+18+2+20

89-65-21

96-14-22

34+45+16

43+27

90-16

70-52

Удобно записывать пример столбиком. Для вас у меня подготовлена маленькая подсказка.

Помните о том, что единицы подписываем под единицами, десятки – под десятками. Не забывайте ставить над десятками точку, если занимаем 1 десяток, ставить единичку, если запоминаем один десяток.

Задание 2. Реши с объяснением, записывая столбиком.

43+12

56+24

27+38

37-21

95-69

40-16

Классы чисел

Разряды чисел объединяются в классы. В каждом классе есть три разряда: единицы, десятки и сотни.

Первый класс называется классом единиц. Сюда входят числа до тысячи.

Второй класс — класс тысяч. Единицы, десятки и сотни здесь используются для обозначения количества тысяч в числе.

1 000 — одна тысяча.

25 000 — двадцать пять тысяч, то есть, два десятка и пять тысяч.

347 000 — триста сорок семь тысяч, то есть три сотни, семь десятков и семь тысяч.

Третий класс — класс миллионов, а четвёртый — класс миллиардов.

Пример:

Число 258 317 521

В этом числе три класса: миллионов, тысяч и единиц. В каждом классе мы видим по три разряда: сотен, десятков и единиц. Пробуем прочитать это число: двести пятьдесят восемь миллионов триста семнадцать тысяч пятьсот двадцать один.

То есть, это две сотни миллионов, пять десятков миллионов, восемь миллионов, три сотни тысяч, один десяток тысяч, семь тысяч, пять сотен единиц, два десятка единиц и единица.

Примечание: обычно при написании крупных чисел ставятся небольшие пробелы между классами. Это делается, чтобы такие числа было удобнее читать и чтобы зрительно было проще отделять один класс от другого.

Практика:

Предложите ребёнку разложить на классы и разряды следующие числа:

3 967, 12 508, 17 834 552.

Дроби и их запись

Дробь – это числовое значение, которое представляет собой часть целого числа. Она записывается в виде дробной черты, которая обозначает отношение между числителем и знаменателем.

Числитель – это верхняя часть дроби, которая обозначает количество частей целого числа. Знаменатель – это нижняя часть дроби, которая обозначает на сколько частей разбито целое число.

Дробь можно записывать в виде обыкновенной дроби или десятичной дроби. В обыкновенной дроби числитель и знаменатель разделяются дробной чертой, например: 2/3, 5/8. В десятичной дроби число разбивается на десятичные доли, которые записываются после запятой, например: 0,6, 0,125.

Дроби могут быть эквивалентными, что означает, что они имеют одинаковое значение, но разные записи. Например, 2/3 и 4/6 – это эквивалентные дроби, потому что они равны 0,666666… или 2/3. Для упрощения дробей можно сокращать числитель и знаменатель на общий делитель.

Дроби с одинаковыми знаменателями можно сравнивать по значениям их числителей. Например, 1/4 < 2/4 < 3/4.
Дроби с разными знаменателями нужно приводить к общему знаменателю, чтобы сравнить их по величине. Например, 1/4 > 1/5, потому что 5 является меньшим знаменателем, чем 4.

В математике 4 класса дроби используются для решения задач, вычисления площади и периметра фигур, а также в различных формулах и уравнениях.

Разряды счётных единиц. Видеоурок. Математика 3 Класс

Рассмотрим, как связаны между собой счётные единицы (рис. 1).

Рис. 1. Взаимосвязь счетных единиц (Источник)

При записи числа каждая счётная единица записывается на своём месте (табл. 1).

Таблица 1. Запись трёхзначных чисел

3 разряд	2 разряд	1 разряд
сотни	десятки	единицы

Разряды считаются справа налево, начиная с первого разряда – единицы. Второй разряд – десятки. И третий разряд – сотни.

Запишите числа, отложенные на счётах, (рис. 2, 3, 4) и прочитайте их.

Рис. 2. Числа

Рис. 4. Числа

Рис. 3. Числа

Решение: 1. На счётах отложено семь единиц, два десятка и три сотни. Получается число триста двадцать семь.

327

2. В следующем числе (рис. 3) единицы отсутствуют. Если нет какого-либо разряда, можно поставить ноль. Всё число – триста двадцать.

320

3. На рисунке 4 в числе семь единиц, нет десятков и три сотни. Получается число триста семь.

307

Прочитайте числа и объясните, что обозначает каждая цифра в записи числа:

1. 894 3. 480

2. 809 4. 900

Решение: 1. Число восемьсот девяносто четыре. В этом числе цифра 4 обозначает четыре единицы. Цифра 9 означает девять десятков. А цифра 8 означает восемь сотен.

2. В числе восемьсот девять цифра 9 означает, что в первом разряде девять единиц. Цифра 0 означает, что единицы второго разряда отсутствуют. А Цифра 8 показывает, что единиц третьего разряда восемь.

3. В числе четыреста восемьдесят цифра 0 указывает, что единицы отсутствуют, десятков восемь, а сотен четыре.

4. В числе девятьсот отсутствуют единицы и десятки, а сотен девять.

Разделите данные числа на 3 группы по какому-либо признаку: 100, 4 , 43, 606, 8 ,61, 999, 250, 3, 57.

Решение: 1. Внимательно посмотрим на числа и разделим их на группы (табл. 2).

Таблица 2. Задание № 4

1 группа

2 группа

3 группа

100

606

999

250

Так, в первой группе оказались все однозначные числа. Во второй группе – двузначные, а в третьей группе все числа трёхзначные.

Запишите числа и прочитайте их:

1. 283 3. 501

2. 460 4. 700

Решение: 1. В числе двести восемьдесят три 2 сотни 8 десятков и 3 единицы.

2. В числе четыреста шестьдесят 4 сотни 6 десятков и нет единиц.

3. В числе пятьсот один 5 сотен 0 десятков и 1 единица.

4. В числе семьсот 7 сотен 0 десятков и 0 единиц.

Выразите данные величины в более крупных единицах измерения:

1. 125 см 3. 86 мм

2. 540 см 4. 42 дм

Решение: 1. Для того чтобы выполнить такой перевод одних единиц измерения в другие, необходимо вспомнить взаимосвязь этих единиц (рис. 5). Применим данные знания к первому выражению. В числе 125 одна сотня – 1 м, два десятка – 2 дм, и пять единиц – 5 см.

125 см = 1 м 2 дм 5 см

Рис. 5. Взаимосвязь единиц измерения (Источник)

2. Во второй величине пятьсот сорок сантиметров. В этом числе 5 сотен – 5 м и 4 десятка – 4 дм, а единицы отсутствуют, следовательно, сантиметров не будет.

540 см = 5 м 4 дм

3. Восемьдесят шесть миллиметров. В одном сантиметре десять миллиметров, значит, в этой величине будет восемь сантиметров и шесть миллиметров.

86 мм = 8 см 6 мм

4. В последнем числе (42 дм) видно четыре десятка и известно, что в 1 м – 10 дм.

42 дм = 4 м 2 дм

Выразите данные величины в более мелких единицах измерения:

1. 1 м 75 см

2. 2 дм 8 мм

Решение: 1. Для решения задания воспользуемся рисунком 5, на котором изображена взаимосвязь между единицами измерения длины.

1 м 75 см = 175 см

2. Переведём второе число.

2 дм 8 мм = 208 мм

Список литературы

Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

All-schools.pp.ua (Источник).
Urokonline.com (Источник).
Uchu24.ru (Источник).

Домашнее задание

Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / – 2-е изд. – М.: Просвещение, 2012., стр. 44, 45 № 1–7.
Выразите в миллиметрах

а) 22 см б) 1 м в) 3 дм 1 см г) 7 см 8 мм
Разделите числа на три группы по какому-либо признаку: 100, 210, 15, 7, 8, 123, 458, 33, 49, 1, 99, 8.
*Прочитай числа и объясни, что обозначает каждая цифра в записи числа:

а) 219 б) 380 в) 407 г) 800.

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример:

А = {а, в, с, у} – А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

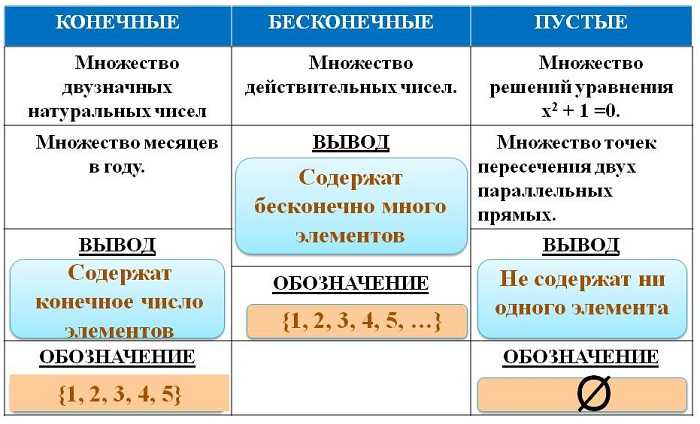
Выделяют три вида множеств:

конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
бесконечные — не являющиеся конечными (например, числовые);
пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.

Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.

Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

F = { Том, Джон, Лео }

Пример 2. Запишем множество делителей числа 6.

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

D = { 1, 2, 3, 6 }

Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:

2 ∈ D

Читается как «2 принадлежит множеству делителей числа 6»

Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:

5 ∉ D

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

{ Том }

Зададим множество, которое состоит из одного числа 2

{ 2 }

Зададим множество, которое состоит из двух чисел: 2 и 5

{ 2, 5 }

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.

N = {9, 11, 13, 15……}.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Z = {-112, -60, -25, 0, 36, 58, 256}.

Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

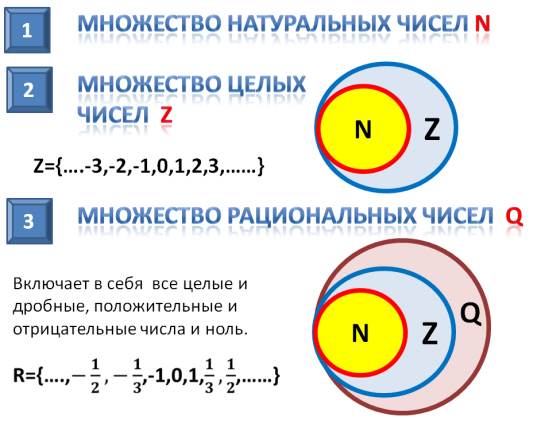
Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Разряды и классы чисел

Разряды

единиц

1…9;

десятков

10…90;

сотен

100…900.

Отсюда видно, что разрядом числа является его позиция в цифровой записи, причём любое значение можно представлять через разрядные слагаемые в виде nnn = n00 + n0 + n, где n — любая цифра от 0 до 9.

Один десяток является единицей второго разряда, а одна сотня — третьего. Единицы первого разряда называются простыми, все остальные являются составными.

Для удобства записи и передачи применяется группировка разрядов в классы по три в каждом. Между классами для удобства чтения допускается ставить пробел.

Классы

Первый — единиц, содержит до 3 знаков:

200 + 10 +3 = 213.

Двести тринадцать содержит в себе следующие разрядные слагаемые: две сотни, один десяток и три простых единиц.

40 + 5 = 45;

Сорок пять состоит из четырёх десятков и пяти простых единиц.
Второй — тысяч, от 4 до 6 знаков:

679 812 = 600 000 + 70 000 + 9 000 + 800 +10 + 2.

шестьсот тысяч;
семьдесят тысяч;
девять тысяч;
восемьсот;
десять;
два;

3 456 = 3000 + 400 +50 +6.

Здесь отсутствуют слагаемые выше четвёртого разряда.

Третий — миллионов, от 7 до 9 цифр:

887 213 644;

Это число содержит девять разрядных слагаемых:

800 миллионов;
80 миллионов;
7 миллионов;
200 тысяч;
10 тысяч;
3 тысячи;
6 сотен;
4 десятка;
4 единицы;

7 891 234.

В этом числе нет слагаемых выше 7 разряда.

Четвёртый — миллиардов, от 10 до 12 цифр:

567 892 234 976;

Пятьсот шестьдесят семь миллиардов восемьсот девяносто два миллиона двести тридцать четыре тысячи девятьсот семьдесят шесть.

Разрядные слагаемые 4 класса читаются слева направо:

единицы сотен миллиардов;
единицы десятков миллиардов;
единицы миллиардов;
сотен миллионов;
десятков миллионов;
миллионов;
сотен тысяч;
десятков тысяч;
тысяч;
простые сотни;
простые десятки;
простые единицы.

Нумерация разряда числа производится начиная с меньшего, а чтение — с большего.

При отсутствии в числе слагаемых промежуточных значений при записи ставятся нули, при произношении названия отсутствующих разрядов, как и класса единиц не произносится:

400 000 000 004;

Четыреста миллиардов четыре. Здесь не произносятся из-за отсутствия следующие названия разрядов: десятого и одиннадцатого четвёртого класса; девятого, восьмого и седьмого третьего и самого́ третьего класса; также не озвучиваются названия второго класса и его разрядов, а также сотни и десятки единиц.

Пятый — триллионов, от 13 до 15 знаков.

487 789 654 427 241.

Читается слева:

Четыреста восемьдесят семь триллионов семьсот восемьдесят девять миллиардов шестьсот пятьдесят четыре миллиона четыреста двадцать семь двести сорок один.

Шестой — квадриллионов, 16—18 цифр.

321 546 818 492 395 953;

Триста двадцать один квадриллион пятьсот сорок шесть триллионов восемьсот восемнадцать миллиардов четыреста девяносто два миллиона триста девяносто пять тысяч девятьсот пятьдесят три.

Седьмой — квинтиллионов, 19—21 знак.

771 642 962 921 398 634 389.

Семьсот семьдесят один квинтиллион шестьсот сорок два квадриллиона девятьсот шестьдесят два триллиона девятьсот двадцать один миллиард триста девяносто восемь миллионов шестьсот тридцать четыре тысячи триста восемьдесят девять.

Восьмой — секстиллионов, 22—24 цифры.

842 527 342 458 752 468 359 173

Восемьсот сорок два секстиллиона пятьсот двадцать семь квинтиллионов триста сорок два квадриллиона четыреста пятьдесят восемь триллионов семьсот пятьдесят два миллиарда четыреста шестьдесят восемь миллионов триста пятьдесят девять тысяч сто семьдесят три.

Можно просто различать классы по нумерации, к примеру, число 11 класса содержит в себе при написании от 31 до 33 знаков.

Но на практике запись такого количества знаков неудобна и чаще всего приводит к ошибкам. Поэтому при операциях с такими величинами производится сокращение количества нулей путём возведения в степень. Ведь значительно проще написать 10 31, чем приписывать тридцать один ноль к единице.