Системы счисления

Степени некоторых чисел

Степени числа 2

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2n	1	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16384	32768	65536	131072	262144	524288	1 048 576

2n	Результат	Двоичноепредставление	Нолей(n)	Знаков(n+1)	Значения(штуки)
2	1	1	1	0–1 (2=21)
21	2	10	1	2	0–3 (4=22)
22	4	100	2	3	0–7 (8=23)
23	8	1000	3	4	0–15 (16=24)
24	16	10000	4	5	0–31 (32=25)
25	32	100000	5	6	0–63 (64=26)
26	64	1000000	6	7	0–127 (128=27)
27	128	10000000	7	8	0–255 (256=28)
28	256	100000000	8	9	0–511 (512=29)

1. Выводы (

n+1 — число знаков):

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

Степени некоторых чисел

Осно-вание	Степень
1	2	3	4	5	6	7	8	9	10
2	1	2	4	8	16	32	64	128	256	512	1 024
3	1	3	9	27	81	243	729	2 187	6 561	19 683	59 049
4 (22)	1	4	16	64	256	1 024	4 096	16 384	65 536	262 144
5	1	5	25	125	625	3 125	15 625	78 125	390 625
6	1	6	36	216	1 296	7 776	46 656	279 936
7	1	7	49	343	2 401	16 807	117 649	823 543
8 (23)	1	8	64	512	4 096	32 768	262 144
9 (32)	1	9	81	729	6 561	59 049	531 441
10	1	10	100	1 000	10 000	100 000	1 000 000
11	1	11	121	1 331	14 641	161 051
12	1	12	144	1 728	20 736	248 832
13	1	13	169	2 197	28 561	371 293
14	1	14	196	2 744	38 416	537 824
15	1	15	225	3 375	50 625	759 375
16 (24)	1	16	256	4 096	65 536

Примечание

Восьмеричная система счисления

Восьмеричная система когда-то использовалась наравне с шестнадцатеричной. Из названия понятно, что она использует всего восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричная система подходит для представления шести-, девяти- и двенадцатиразрядных двоичных чисел.

Такие числа встречаются нечасто. Один из самых известных примеров использования восьмеричных чисел — права доступа в операционной системе UNIX. Они записываются девятизначным двоичным числом, например 110100100 или 111101100. Запоминать и передавать такие числа неудобно, поэтому программисты предпочитают восьмеричную систему счисления, и записывают права доступа в виде 644 или 754.

Популярные операционные системы Linux и MacOS берут своё начало в UNIX, поэтому там права доступа также задаются восьмеричным числом.

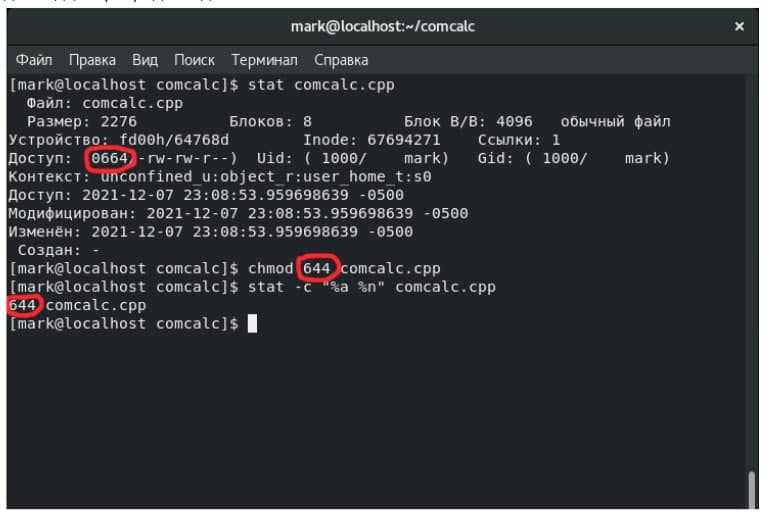
Пользователи UNIX используют команду stat, чтобы узнать права доступа, и команду chmod, чтобы изменить их. На рисунке вы видите, что команды stat и chmod используют восьмеричные числа. Подробный рассказ об этих командах выходит за рамки нашей статьи. Узнаете больше о правах доступа, и о том, что означают эти числа, можно изучив командную строку Linux.

Подводя итог, можно сказать, что восьмеричные числа сейчас используются редко. В подавляющем большинстве случаев программисты используют шестнадцатеричную запись.

Таблицы истинности

При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.

Основные логические операции

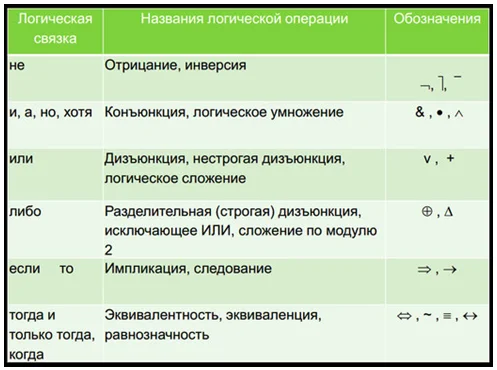
Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.

Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

Фрагмент таблицы истинности для конъюнкции.

Так выражаются условия для всех логических операций.

Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.

Позиционные системы счисления

Рассмотренные системы счисления относятся к классу позиционных систем. В них числовое значение каждой цифры зависит от положения в числе. Например, в десятичном числе 126 единица означает сотню, а в числе 216 единица уже на другом месте и обозначает десять.

Каждое число позиционной системы счисления можно представить как в свернутом виде, например, 126, так и в развернутом: 1*102 + 2*101 + 6*10 , то есть 100 + 20 +6 =126.

Аналогично, двоичное число 111001 = 1*25 + 1*24 + 1*23 + 0*22 + 0*21 + 1*2

Восьмеричное число: 247 = 2*82 + 4*81 + 7*8

Шестнадцатеричное число: 2A5F = 2*163 + A*162 + 5*161 + F*16

Используя развернутую форму, можно переводить числа из любой системы счисления в десятичную систему.

Таблица соответствия чисел систем счисления

система» data-order=»Двоичный система» стиль = «минимальная ширина: 24,6711%»; ширина:24,6711%;»>Двоичный система	система» data-order=»восьмеричный система» стиль = «минимальная ширина: 24,1776%»; ширина:24,1776%;»>восьмеричная система	система» data-order=»Десятичный система» стиль = «минимальная ширина: 22,2039%; ширина:22,2039%;»>Десятичный система	система» data-order=»Шестнадцатеричный система» стиль = «минимальная ширина: 28,9474%»; ширина:28,9474%;»>Шестнадцатеричный система
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	1
11	1011	1. 3	Б
12	1100	14	С
1. 3	1101	15	Д
14	1110	16	Е
15	1111	17	Ф
16	10 000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	1. 3
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1А
27	11011	33	1Б
28	11100	34	1С
29	11101	35	1D
30	11110	36	1Э
31	11111	37	1эт
32	100 000	40	20

Плотность записи информации в позиционных системах счисления[]

При условии равновероятности появления каждой из цифр в записи числа информационная энтропия записи n-значного числа в системе счисления с основанием b принимает значение nln⁡bb{\displaystyle n{\frac {\ln b}{b}}} (с точностью до постоянного коэффициента). Поэтому плотность записи (т.е. количество информации на одну позицию) чисел в системе счисления с основанием b равна ln⁡(b)b{\displaystyle {\frac {\ln(b)}{b}}}.

Плотность записи, как функция от b, принимает максимальное значение в точке при b=e=2,718281828…{\displaystyle e=2,718281828\ldots }.
Таким образом, наибольшей плотностью записи информации обладает система счисления с нецелочисленным основанием равным e. Из систем счисления с целочисленными основаниями наибольшей плотностью записи информации обладает троичная система счисления. Двоичная и четверичная системы счисления делят второе место. Остальные целочисленные системы счисления имеют меньшую плотность записи информации.

Использование шестнадцатеричной системы

По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы. Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:

• Ссылки на цвета в HTML и CSS
• Язык ассемблера
• Сообщения об ошибках

Цвета

Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.

Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF.  В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.

• #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.
• Черный это #000000 — ни красного, ни зеленого, ни синего.
• Белый — это #FFFFFF — при смешении всех цветов.

Системы счисления – виды, особенности

Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.

Все существующие системы делят на 2 группы:

1. Позиционные системы счисления – такие, в которых, в зависимости от положения, цифры будет иметь разное значение. К этой группе относится арабская СС, в которой на первом месте справа цифра будет обозначать единицы, на втором – десятки, на третьем – сотни и так далее.

Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.

К этой группе также относятся СС с различными основаниями (2,8,16).

2. Непозиционные СС – имеет значение именно знак, а не его положение. Единицы, десятки, сотни обозначаются определенными символами. Яркий представитель этой группы – римская СС.

Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.

12 – XII

8 – VIII или IIX

Правильным считается тот вариант, при котором получается меньше символов.

Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.

Алфавит СС – знаки, которые используются для обозначения цифр.

Основание – количество знаков, которыми кодируются числа.  Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.

Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 12548, 011001112

Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).

Разряд – положение, позиция обозначения цифры в числе. Пример?

Общепринятые системы счисления

Человечество в ходе своего развития со временем стало нуждаться в способах подсчета. Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.

Общепринятые системы счисления

В дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.

С течением времени возникла необходимость в символьном обозначении любого количества больше единицы. В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.

Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления. Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.

Узнай, какие ИТ — профессии входят в ТОП-30 с доходом от 210 000 ₽/мес

Павел Симонов
Исполнительный директор Geekbrains

Команда GeekBrains совместно с международными специалистами по развитию карьеры
подготовили материалы, которые помогут вам начать путь к профессии мечты.

Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в
IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее
будущее!

Скачивайте и используйте уже сегодня:

Павел Симонов
Исполнительный директор Geekbrains

Топ-30 самых востребованных и высокооплачиваемых профессий 2023

Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ бесплатных нейросетей для упрощения работы и увеличения заработка

Только проверенные нейросети с доступом из России и свободным использованием

ТОП-100 площадок для поиска работы от GeekBrains

Список проверенных ресурсов реальных вакансий с доходом от 210 000 ₽

Получить подборку бесплатно

pdf 3,7mb
doc 1,7mb

Уже скачали 22321

Любая система счисления принадлежит к одной из двух категорий:

Позиционные СС

Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).

Непозиционные СС

Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы. Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.

К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.

Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.

Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.

Непозиционные СС

Когда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.

Перевод чисел из одной системы счисления в другую

Пусть X — число в системе счисления с основанием s, которое требуется
представить в системе с основанием h. Удобно различать два случая.

В первом случае
и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования
состоит в представлении числа в виде
многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления
с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный
приём иллюстрируют следующие примеры:

.

.

В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.

Во втором случае ()
удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел
и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части
переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.

Перевод целых чисел

Правила перевода целых чисел становится ясным из общей формулы записи числа
в произвольной позиционной системе. Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h:

.

Для нахождения значений разделим
этот многочлен на h:

.

Как видно, младший разряд
, то есть , равен первому остатку.
Следующий значащий разряд определяется
делением частного на h:

.

Остальные также
вычисляются путём деления частных до тех пор, пока
не станет равным нулю.

Для перевода целого числа из s-ичной системы счисления в h-ичную
необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h)
до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит
последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в
последовательности, обратной их получению.

Пример 1. Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы.

Решение:

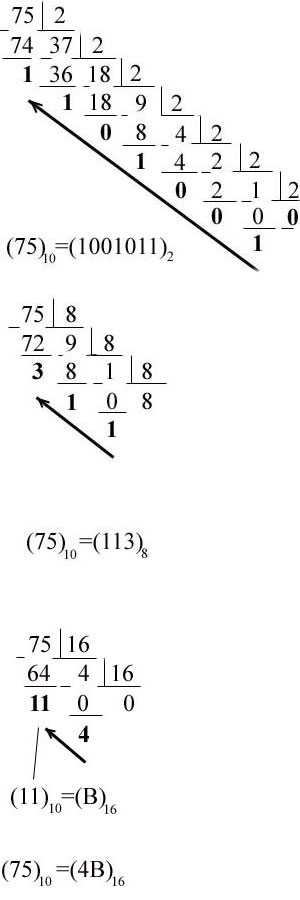
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.

Перевод правильных дробей

Правильную дробь ,
имеющую в системе с основанием s вид ,
можно выразить в системе счисления с основанием h как многочлен вида

Старшая цифра может быть
найдена умножением этого многочлена на h, т.е.

Если это произведение меньше 1, то цифра равна 0,
если же оно больше или равно 1, то цифра равна
целой части произведения. Следующая цифра справа
определяется путём умножения дробной части указанного выше произведения на h и выделения
его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь
по основанию h конечным набором цифр.

Для перевода правильной дроби из системы счисления
с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части
получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных
произведений дают последовательность цифр дроби в h-системе счисления.

Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения
не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в
h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления
будет последовательности целых частей полученных произведений, записанных в порядке их получения и
изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p
знаков после запятой равняется .

Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления.

* В двоичную систему:

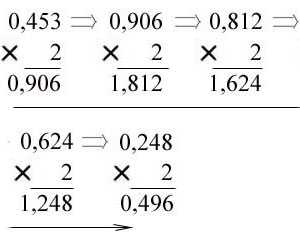
Ответ:

** В восьмеричную систему:

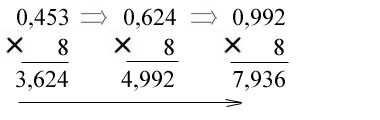
Ответ:

*** В шестнадцатеричную систему:

Ответ: так как , то

Поделиться с друзьями

Правила перевода из одной системы счисления в другую.

Далее последовательно разбирается перевод систем счисления.

1. Перевод целых десятичных чисел в любую другую систему счисления.

Число нужно разделить на новое основание системы счисления. Первый остаток от деления — это и есть первая младшая цифра нового числа. Если частное от деления меньше или равно новому основанию, то его (частное) нужно снова разделить на новое основание. Деление нужно продолжать, пока не получим частное меньше нового основания. Это есть старшая цифра нового числа (нужно помнить, что, например, в шестнадцатиричной системе после 9 идут буквы, т.е. если в остатке получили 11, нужно записать его как B).

Пример («деление уголком»): Переведем число 173₁₀ в восьмеричную систему счисления.

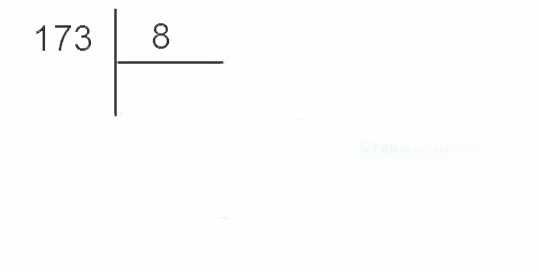
Таким образом, 173₁₀=255₈

2. Перевод правильных десятичных дробей в любую другую систему счисления.

Число нужно умножить на новое основание системы счисления. Цифра, перешедшая в целую часть — старшая цифра
дробной части нового числа. для получения следующей цифры дробную часть получившегося произведения опять нужно
умножать на новое основание системы счисления, пока не произойдет переход в целую часть. Умножение продолжаем,
пока дробная часть не станет равна нулю, либо пока не дойдем до указанной в задаче точности («… вычислить
с точностью, например, двух знаков после запятой»).

Пример: Переведем число 0,65625₁₀ в восьмеричную систему счисления.

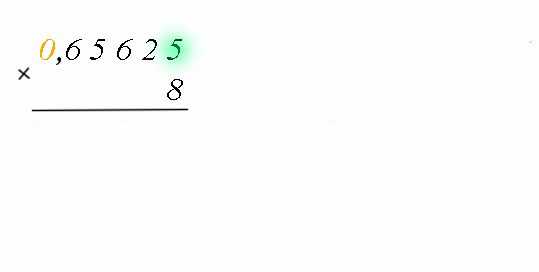
Таким образом, 0,65625₁₀=0,52₈

3. Перевод смешаных десятичных чисел в любую другую систему счисления.

Переводим отдельно целую часть, отдельно дробную — записываем в одно число.

Пример: Переведем число 17,25₁₀ в восьмеричную систему счисления.

По аналогии с пунктом 1: 17₁₀ = 21₈

По аналогии с пунктом 2: 0,25₁₀ = 0,2₈

«Склеиваем» два числа и получаем ответ: 17,25₁₀ = 21,2₈.

4. Перевод чисел из любой системы счисления в десятичную.

Числа необходимо представить в разложении по степеням той системы счисления, в которой находится число, при чем
цифры числа необходимо записать в десятичном эквиваленте. Найти арифметическую сумму.

Пример: Переведем число 1011,01₂ в десятичную систему счисления.

1) Чтобы представить число в разложении по степеням, нужно найти запятую и проставить «карандашиком»
влево и вправо от запятой степени над цифрами числа (слева — неотрицательные степени, т.е. начинаем с нуля;
справа — отрицательные, начиная с -1):

13 02 11 1,
0-1 1-2₂

2) Далее умножаем каждую цифру на основание системы счисления, в которой находится число, возведенное
в соответствующую «подписанную» степень (помним, что любое число в нулевой степени — это единица):

1011,01₂ = 1*23 + 0*22 + 1*21 +
1*2 + 0*2-1 + 1*2-2 = =
8 + 0 + 2 + 1 + 0 + 1/22 = 11 + 1/4 = 11 + 0,25 = 11,25₁₀

Ответ: 11,25₁₀.

5. Перевод чисел из восьмеричной системы счисления в двоичную.

Каждую цифру восьмеричного числа нужно заменить соответствующей двоичной триадой ( * * * ) —
например, для цифры 7 — 111, для 3 — 011. Незначащие нули можно отбросить.

Пример: Переведем число 274,06₈ в двоичную систему счисления.

Просто заменяем все числа триадами:

2 7 4, 0 6 -> 010 111 100, 000 110

274,06₈ = 10111100,00011₂

Ответ: 10111100,00011₂.

6. Перевод чисел из двоичной системы счисления в восьмеричную.

Несложно догадаться, что на этот раз мы просто разбиваем число на триады и заменяем
восьмеричными цифрами (помним, что разбивать начинаем «от запятой» влево и вправо; там, где не хватает дополняем незначащими нулями).

Пример: Переведем число 1111,0110011₂ в восьмеричную систему счисления.

Разбиваем на триады и заменяем:

001’111,011’001’100 -> 1’7,3’1’4

1111,0110011₂ = 17,314₈

Ответ: 17,314₈.

Откуда же появились эти «триады»?

Да это же степень, в которую нужно возвсти двойку, чтобы получить основание 8!

Очевидно, что для шестнадцатиричной системы счисления появятся тетрады («тетра» — четыре) и т.д.

4 = 22
8 = 23	Триады
16 = 24	Тетрады
32 = 25

7. Перевод чисел из двоичной системы счисления в шестнадцатиричную и обратно.

Перевод чисел из двоичной системы счисления в шестнадцатиричную и обратно выглядит так же,
как и для пути «восьмеричная двоичная». Отличие состоит лишь в использовании тетрад ( * * * * ).

Пример: Переведем число CD2,04₁₆ в двоичную систему счисления.

Разбиваем и заменяем:

C’D’2, 0’4 -> 1100’1101’0010, 0000’0100

CD2,04₁₆ = 110011010010,000001₂

Ответ: 110011010010,000001₂.

Виды

Существуют различные типы СС:

1. Непозиционный. В них его значение не зависит от его положения.
2. Позиционно. «Исход» зависит от того, как именно расположен тот или иной компонент.
3. Однородный.
4. Неоднородный.

Каждый вариант имеет свои ключевые особенности.

Позиционный тип

Здесь значение каждой цифры будет зависеть от цифры в номере. Пример — 10-й СС известен человеку. Она позиционно определена. 453 считается примером. Здесь 4 — сотни, обозначающие 400, 5 — десятки (50), 3 — единицы (3). Чем больше число, тем выше будет значение.

Непозиционный тип

Самая старая версия. Каждый компонент представляет собой отдельное значение. Это не зависит от категории. В программировании не используется, поэтому рассматривать его более подробно не рекомендуется.

Однородный тип

Однородный вариант — это такой, в котором набор допустимых символов для всех позиций в номере будет одинаковым. Примером является десятичная система. Чтобы написать элемент, вы можете использовать только одну цифру в каждой цифре. А именно от 0 до 9. Запись 450 разрешена (1 цифра — 0, 2 — 5, 3. — 4), а 4F5 — нет.

Смешанный тип

Это позволяет другой набор других позиций в каждой категории. Примером является измерение времени:

• в секундах — 60 символов;
• в часах — 24;
• в сутки — 365.

Теперь мы можем оценить, какие СС чаще всего встречаются в информатике.

Перевод чисел

Данное действие можно считать самым простым из всех, относящихся к системам счисления.
Каждая цифра числа образует слагаемое, которое надо записать, а потом произвести необходимые арифметические действия.

Прежде чем перейти к конкретным рассуждениям, надо отметить, что приводимые в заданиях числа, обычно не превышают 1024₁₀ или ненамного больше этого значения.
Это связано с разумным ограничением сложности вычислений.

n	1	2	3	4	5	6	7	8	9	10
2n	1	2	4	8	16	32	64	128	256	512	1024
n2*	1	10	100	1000	10000	100000	…

Любое из производимых действий будет замкнуто на эту таблицу!

В десятичную систему

Вне зависимости от обсуждаемой системы счисления, любое число можно разбить на разряды, каждый из которых вносит определенный вклад в значение числа.
Общей закономерностью является то, что чем правее стоит цифра, тем меньшее значение она подразумевает.

В качестве первого примера рассмотрим число 1111_n

В качестве второго примера рассмотрим число 1234_n

Общая формула для перевода:

a₁*n
+ a₂*n1
+ a₃*n2
+ a₄*n3
+ … + a_k*nk–1

где n — основание системы счисления, k — номер разряда числа.

Из десятичной системы

1. Остаток от деления

Последовательно делим число на основание до тех пор, пока не получим частное, равное нулю.
Остатки записываем.
После завершения вычислений записываем значения остатков
в обратном порядке. Полученное число и будет ответом.

Разложим два числа: 23 и 64.

Делимое	Остаток	Смысл действия
23105210	11101	23/2 = 22/2 + 1 = 11 + 111/2 = 5 + 15/2 = 4/2 + 1 = 2 + 12/2 = 1 + 1/2 = 0 + 1

₁₀₂

Делимое	Остаток	Смысл действия
64321684210	0000001	64/2 = 32 + 32/2 = 16 + 16/2 = 8 + 8/2 = 4 + 4/2 = 2 + 2/2 = 1 + 1/2 = 0 + 1

₁₀₂

В некоторых учебниках (например, Босовой) предлагается таблицу записи располагать горизонтально, что очень удобно для сравнительно небольших чисел (11).

В верхней строке записывается число. Остаток от деления (в нашем случае на 2) записывается под ним, а целая часть частного — в следующей колонке.

Делимое	23	11	5	2	1
Остаток	1	1	1	1

₁₀₂

Способом деления можно перевести число в любую систему счисления. Давайте переведем 44 в троичную систему.

Делимое	44	14	4	1
Остаток	2	2	1	1

₁₀₃

Трудно сказать, насколько комфортно ощущают себя люди, производящие привычное деление столь необычным образом.
Лично я испытываю значительный дискомфорт, особенно при переводе не в двоичную систему.

Поэтому, давайте перейдем к другому, менее «магическому» способу.

2. Разложение

Как известно, любое число можно представить в виде суммы чисел.

Таким образом становиться ясно, что для этих вычислений нужно

Порядок действий на практике

Пример 1. Переведем 900 в семеричную систему.

Пример 2. Переведем 900 в пятеричную систему.

Пример 3. Переведем 900 в двоичную систему.

В связи с довольно большой трудоемкостью, данный метод едва ли можно назвать слишком простым
для двоичной системы. Но он вполне понятен и, из-за необходимости четкой записи, всегда может быть легко проверен.

В некоторых случаях, когда число очень мало отличается от степени основания, перевод может оказаться значительно более быстрым, чем другие способы.

Из двоичной в восьми- и шестнадцатеричную системы

Это действие является основным для многих заданий. К сожалению, большинство учебников предлагает зазубрить примерно следующий принцип.

Для перевода из двоичной системы счисления в восьмеричную следует разбить двоичное число по три разряда справа налево.

Необходимо заметить, что 8 = 23, а 16 = 24. Именно поэтому в приведенном правиле и используются группы по три разряда, а для перевода в 16-ричную потребуются уже 4 разряда.

Внимательный читатель может заметить, что еще осталось 4 = 22. То есть двоичную систему также легко можно преобразовать и в четверичную.

Отсюда же следует, что раз 9 = 32, то троичная система легко преобразуется в девятеричную, если разбить её число на пары.

Как это делается на практике.

Факультативный материал по переводу в четверичную систему.

₂₄

Из восьми и шестнадцатеричной систем в двоичную

Все также, как и в предыдущем разделе, только каждая цифра восьмеричного числа
превращается в три двоичных цифры, а шестнадцатеричного — в четыре.

Типичной ошибкой является незаписывание ведущих нулей (10 вместо 010).

Буквально пара слов о системах счисления и математике: сколько в числе нолей в конце, столько раз оно делится без остатка на основание системы.

Шестнадцатеричная система счисления

Основание этой системы счисления p равно шестнадцати. Эту систему счисления можно считать ещё одним вариантом записи
двоичного числа. В этой системе счисления используется шестнадцать цифр. Здесь уже не хватает десяти цифр, поэтому
приходится придумать недостающие шесть цифр.

Для обозначения этих цифр можно воспользоваться первыми буквами латинского алфавита

При записи шестнадцатеричного
числа неважно буквы верхнего или нижнего регистра будут использоваться в качестве цифр. В качестве цифр в шестнадцатеричной
системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Так как здесь появляются новые цифры, то приведём таблицу соответствия этих цифр десятичным значениям.

Таблица 6. Таблица соответствия шестнадцатеричных цифр десятичным значениям

Шестнадцатеричная цифра	Десятичный эквивалент
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
A	10
B	11
C	12
D	13
E	14
F	15

Число в этой системе счисления записывается как сумма единиц, чисел шестнадцать, двести пятьдесят шесть и так далее. То
есть веса соседних разрядов различаются в шестнадцать раз. Точно также записываются и числа, меньшие единицы. В этом случае
разряды числа будут называться как шестнадцатые, двести пятьдесят шестые и так далее доли единицы.

Рассмотрим пример записи шестнадцатеричного числа:

₁₆₁₆21-1-2_{1010101010101010}

Из приведённых примеров записи чисел в различных системах счисления вполне очевидно, что для записи одного и того же
числа с одинаковой точностью в разных системах счисления требуется различное количество разрядов. Чем больше основание
системы счисления, тем меньшее количество разрядов требуется для записи одного и того же числа.

Дата последнего обновления файла
11.02.2020

Симметричные позиционные системы счисления[]

Такие системы счисления отличаются от обычных тем, что используют цифры не из множества (,…,b−1){\displaystyle (0,\ldots ,b-1)}, а из множества (−b−12,−b−32,…,b−12){\displaystyle (-{\frac {b-1}{2}},-{\frac {b-3}{2}},\ldots ,{\frac {b-1}{2}})}. Чтобы цифры были целыми, нужно, чтобы b было нечётным. В симметричных системах счисления не требуется дополнительных обозначений для знака числа. Кроме того, вычисления в симметричных системах удобны тем, что не требуется особых правил округления — оно сводится к простому отбрасыванию лишних разрядов, что резко уменьшает систематические ошибки вычислений.

Чаще всего используется симметричная троичная система счисления с цифрами (-1,0,1). Она применяется в троичной логике и была технически реализована в вычислительной машине «Сетунь».

Запись рациональных чисел[]

Рациональное число x в b-ричной системе счисления представляется в виде линейной комбинации (вообще говоря, бесконечной) степеней числа b:

x=an−1an−2…a1a,c1c2…=∑k=n−1akbk+∑k=1∞ckb−k{\displaystyle x=a_{n-1}a_{n-2}\ldots a_{1}a_{0},c_{1}c_{2}\ldots =\sum _{k=0}^{n-1}a_{k}b^{k}+\sum _{k=1}^{\infty }c_{k}b^{-k}}

где ak{\displaystyle a_{k}} — цифры целой части дробного числа (до запятой), ck{\displaystyle c_{k}} — цифры дробной части дробного числа (после запятой), n — число разрядов целой части дробного числа (до запятой).

Только числа, представимые в виде qbm{\displaystyle {\frac {q}{b^{m}}}} для целых m и q, обладают конечной записью в b-ричной системе счисления.