Примечания и ссылки
- ↑ см. Ссылки на статью Giovanni Ceva (см. Giovanni Ceva, De lineis rectis se invicem secantibus statica constructio )
- ↑ (in) Январь Хогендийк , «Аль-Мутаман ибн Худ, 11 век, король Сарагосы и блестящий математик», в Historia Mathematica , Vol. 22, 1995, с. 1–18
- ↑ (in) JP Hogendijk , «Открытие геометрической компиляции XI века: Истикмаль Мутамана ибн Юсуфа аль-Худа, короля Сарагосы», в Historia Mathematica , Vol. 13, 1986, с. 43-52
- ↑ Это определение не универсально, в некоторых произведениях это сегмент, а в других Cévienne встречается в более общем плане с линией, проходящей с противоположной стороны, см., Например, Coxeter and Greitzer, первую главу и глоссарий.
- ↑ относительно площади данного треугольника, мы используем определитель , см., Например, (en) HSM Coxeter , Introduction to Geometry , глава по аффинной геометрии.
Как пользоваться порталом «1С:Урок»
Ресурсы портала поддерживают проведение занятий при разной технической оснащенности: компьютер с проектором на рабочем месте учителя,
компьютер на группу учащихся,
компьютер или планшет у каждого учащегося,
онлайн-обучение.
Ресурсы портала воспроизводятся на всех основных носителях: компьютеры и ноутбуки под управлением Windows, Linux, MacOS,
планшеты под управлением iOS и Android,
интерактивные доски.
Выбирайте ресурсы для своих занятий в нашей библиотеке.
Демонстрируйте отобранные ресурсы из раздела Мои материалы.
Создавайте свои интерактивные ресурсы при помощи конструкторов и делитесь ими с коллегами и учениками.
Изучайте методические материалы с примерами занятий, чтобы сделать ваши уроки ещё лучше.
Следите за новостями на сайте и в соцсетях, чтобы быть в курсе обновлений и мероприятий.
Изучите подробные инструкции по работе с порталом.
Применения теоремы Чевы
В разделе нашего справочника «Медиана треугольника» доказана теорема о том, что медианы треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим медианы AA1, BB1 и CC1 треугольника ABC (рис.9).
то выполнено равенство
откуда вытекает, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема доказана.
В разделе нашего справочника «Окружность, вписанная в треугольник» доказана теорема о том, что биссектрисы треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим биссектрисы AA1, BB1 и CC1 треугольника ABC (рис.10).
В соответствии со свойством биссектрисы справедливы равенства
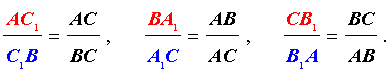
Если перемножить эти три равенства, то мы получим равенство
из которого вытекает, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема доказана.
В разделе нашего справочника «Высота треугольника» доказана теорема о том, что высоты треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим сначала высоты AA1, BB1 и CC1остроугольного треугольника ABC (рис.11).
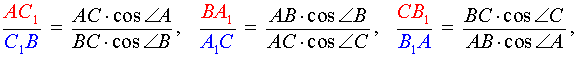
то, перемножив эти три равенства, мы получим равенство
из которого вытекает, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема о пересечении высот остроугольного треугольника доказана.
Теперь рассмотрим случай тупоугольного треугольника (рис. 12).
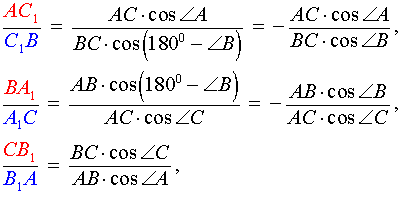
то, перемножив эти три равенства, мы получим равенство
из которого вытекает, что прямые AA1, BB1 и CC1 пересекаются в одной точке. Теорема о пересечении высот тупоугольного треугольника доказана.
Доказывать теорему о том, что в случае прямоугольного треугольника все высоты пересекаются в одной точке не нужно, поскольку все высоты прямоугольного треугольника пересекаются в вершине прямого угла.
Теорема о пересечении высот треугольника доказана полностью.
Теперь с помощью теоремы Чевы докажем следующую теорему.
Из этих равенств получаем:
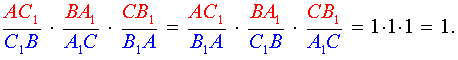
Отсюда с помощью теоремы Чевы заключаем, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема доказана.
1 Формулировка теоремы Менелая
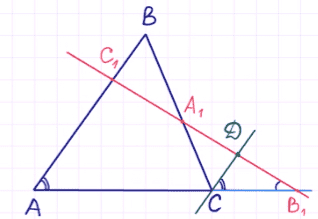
Пусть прямая пересекает треугольник $ABC$, причем $C’$ – это точка ее пересечения со стороной $AB$ , $B’$ – точка ее пересечения со стороной $AC$ и $A’$ – точка ее пересечения с продолжением стороны $BC$ (рис. 1). Тогда имеет место соотношение:
$$ bigg (frac {AC’} {C’B} bigg ) cdot bigg ( frac {BA’} {A’C} bigg ) cdot bigg ( frac {CB’} {B’A} bigg ) = 1$$
Доказательство теоремы Менелая очень простое. Например, один из распростаненных способов доказательства требует всего одного дополнительного построения. Через вершину $C$ проведите прямую, параллельную $AB$, и воспользуйтесь двумя парами подобных треугольников, которые при этом получаются. Недавно я записал видео с доказательством:
Справедлива также обратная теорема Менелая.
Формулировка теоремы Менелая
Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.
Прежде чем приступить к проработке, сделаем соответствующий рисунок.
Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.
Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.
Если мы видим приведённый выше рисунок, можно записать формулу:
Запомнить отношение просто: действуем по принципу «вершина – точка, точка – вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:
Доказательство теоремы
Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:
Обозначим точку пересечения данной прямой с B1C1 через точку D.
В таком случае мы получим несколько пар подобных треугольников.
Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B1 между ними.
Углы B1CD и B1AC1 равны как соответственные при параллельных прямых CD, AB и секущей AC.
Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:
Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.
Используя описанное равенства, применив свойства пропорции, запишем:
Запишем следующую пару подобных треугольников: треугольники CDA1 и BC1A1 подобны, так как углы CA1D и BA1C1 равны как вертикальные. Кроме этого, угол CDA1 равен углу BC1A1, как накрест лежащие при параллельных прямых CD, AB и секущей C1D.
Покажем это на рисунке:
Из данного подобия можно записать некоторую пропорциональность сходственных сторон:
Так же выразим CD:
Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.
Таким образом получаем:
Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:
Что и требовалось доказать.
Примеры применения
Теорема Чевы позволяет доказать многие свойства совпадающих прямых.
- Мы можем применить это к простому случаю, например, к точке пересечения медиан . В этом случае D является средней точкой [ BC ] и, следовательно, BD = DC . То же самое и с остальными пунктами. Все отношения, используемые в теореме, равны 1, а значит, и их произведение, что доказывает, что медианы треугольника совпадают.
- Изогональное объединены и isotomiques два примера применения теоремы Чевы.
- Прямые, соединяющие вершины треугольника с точками контакта вписанной окружности, совпадают с точкой Жергонна этого треугольника.
- Линии, соединяющие каждую вершину треугольника с точкой контакта окружности, вписанной со стороной, противоположной этой вершине, совпадают в точке Нагеля этого треугольника.
Пример задачи
Дан треугольник ABC с точками A’, B’ и C’ на сторонах BC, AC и AB соответственно. Вершины треугольника соединяются с заданными точками, а образующиеся отрезки проходят через одну точку. Точки А’ и В’ взяты на серединах соответствующих противоположных сторон. Выясните, в каком отношении точка С’ делит сторону АВ.
Решение
Нарисуем рисунок по условиям задачи. Для простоты используем следующие обозначения:
- АВ’ = В’С = а
- ВА’ = А’С = б
Остается только составить связь между отрезками по теореме Чевы и подставить в нее принятые обозначения: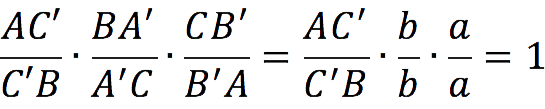
После сокращения дробей получим:
Следовательно, AC’ = C’B, т е точка C’ делит сторону AB пополам.
Следовательно, отрезки АА’, ВВ’ и СС’ являются медианами нашего треугольника. После решения задачи мы доказали, что они пересекаются в одной точке (справедливо для всех треугольников).
Примечание: с помощью теоремы Чевы можно доказать, что в треугольнике в одной точке также пересекаются биссектрисы или высоты.
Задача 1
Дан треугольник ABC (см рисунок ниже) с удлиненной стороной CA. Также были взяты медианы BM и AN. Обозначим их точку пересечения через О.
Возьмем точку K на стороне AB так, что AK относится к AB как 1/3.
АС=4 см, АМ=2 см.
Проведем прямую ОК до пересечения со стороной АС. Обозначим их точку пересечения как P.
Сторона AP будет обозначаться y.
Найти: что такое сегмент AP.
Решение:
Так как отношение сторон АВ и АК равно 1/3, то АК = х и КБ = 3х.
Рассмотрим треугольник АВМ. Для этого мы берем это прямо OP.
Таким образом, мы нашли искомые точки P, A, M, O, K и B.
Запишем теорему Менелая для этой фигуры.
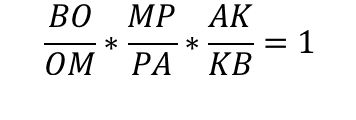
Подставим известные данные в это соотношение:
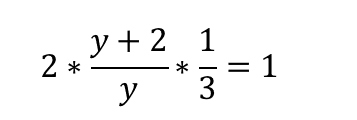
В результате получаем, что у = 4.
Ответ: отрезок АР = 4 см.
Задача 2
Проблема, связанная со свойствами теоремы Чевы.
Рассмотрим рисунок:
Данный:
- сумма АВ и ВС равна 13;
- АС = 8 см.
Найти: соотношение между БО и ОБ1.
Итак, напишем отношение:
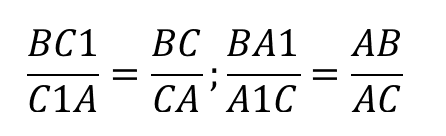
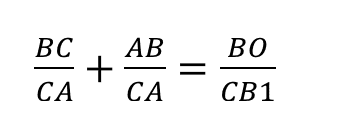
Мы заменяем:
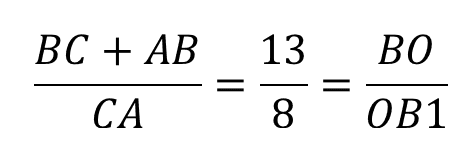
Конечным результатом является дробь 13/8.
Отвечать:
Применения теоремы Чевы
В разделе «Медианы треугольника» нашего справочника доказана теорема о том, что медианы треугольника пересекаются в одной точке. Приведем другое доказательство этой теоремы, основанное на теореме Чевы. Для этого рассмотрим медианы AA1, BB1 и CC1 треугольника ABC (рис. 9).
Рис.9
Потому что
тогда равенство
,
откуда следует, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема доказана.
В разделе нашего справочника «Окружность, вписанная в треугольник» доказана теорема о том, что биссектрисы треугольника пересекаются в одной точке. Приведем другое доказательство этой теоремы, основанное на теореме Чевы. Для этого рассмотрим биссектрисы AA1, BB1 и CC1 треугольника ABC (рис. 10).
Рис.10
В соответствии со свойством биссектрисы истинны подобия
Если мы умножим эти три равенства, то получим равенство,
откуда следует, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема доказана.
В разделе нашего справочника «Высота треугольника» доказана теорема о том, что высоты треугольника пересекаются в одной точке. Приведем другое доказательство этой теоремы, основанное на теореме Чевы. Для этого сначала рассмотрим высоты AA1, BB1 и CC1 остроугольного треугольника ABC (рис. 11).
Рис. 11
Потому что
значит, умножая эти три равенства, получаем равенство,
откуда следует, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Доказана теорема о пересечении высот остроугольного треугольника.
Теперь рассмотрим случай тупоугольного треугольника (рис. 12).
Рис. 12
На рис. 12 изображен треугольник ABC с тупым углом B, высотами которого являются отрезки AA1, BB1 и CC1.
Потому что
значит, умножая эти три равенства, получаем равенство,
откуда следует, что прямые AA1, BB1 и CC1 пересекаются в одной точке. Доказана теорема о пересечении высот тупоугольного треугольника.
Нет необходимости доказывать теорему о том, что в случае прямоугольного треугольника все высоты пересекаются в одной точке, так как все высоты прямоугольного треугольника пересекаются в вершине прямого угла.
Теорема о пересечении высот треугольника полностью доказана.
Теперь, используя теорему Чевы, докажем следующую теорему.
Теорема. Рассмотрим ABC как окружность, вписанную в произвольный треугольник. Пусть точки A1, B1 и C1 касаются этой окружности со сторонами BC, AC и AB соответственно. Тогда отрезки AA1, BB1 и CC1 пересекаются в одной точке (рис. 13).
Рис. 13
Доказательство. Используя свойство равенства касательных, проведенных к окружности из одной точки, запишем следующие равенства:
AC1 = B1A, BA1 = C1B, CB1 = A1C.
Из этих сходств получаем:
Отсюда, используя теорему Чевы, заключаем, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Теорема доказана.
Комментарий. Точка пересечения отрезков AA1, BB1 и CC1, упомянутая в только что доказанной теореме, называется точкой Жергонна в честь французского математика Жозефа Жергонна (1771 — 1859 гг.).
Как пользоваться порталом «1С:Урок»
Ресурсы портала поддерживают проведение занятий при разной технической оснащенности: компьютер с проектором на рабочем месте учителя,
компьютер на группу учащихся,
компьютер или планшет у каждого учащегося,
онлайн-обучение.
Ресурсы портала воспроизводятся на всех основных носителях: компьютеры и ноутбуки под управлением Windows, Linux, MacOS,
планшеты под управлением iOS и Android,
интерактивные доски.
Выбирайте ресурсы для своих занятий в нашей библиотеке.
Демонстрируйте отобранные ресурсы из раздела Мои материалы.
Создавайте свои интерактивные ресурсы при помощи конструкторов и делитесь ими с коллегами и учениками.
Изучайте методические материалы с примерами занятий, чтобы сделать ваши уроки ещё лучше.
Следите за новостями на сайте и в соцсетях, чтобы быть в курсе обновлений и мероприятий.
Изучите подробные инструкции по работе с порталом.
Новости
Вебинар для учителей математики
Примите участие в обучающем вебинаре и получите сертификат.
…
Вебинар для учителей обществознания
Примите участие в обучающем вебинаре и получите сертификат.
…
Список ЭОР для рабочей программы учителя математики по обновленному ФГОС
Сохраните подборку цифровых ресурсов по математике и применяйте их на уроках, чтобы сделать занятия современными и интересными для учащихся!
…
Организация исследовательской деятельности на уроках в начальной школе с использованием ЦОР образовательной платформы «1С:Урок»
Опыт создания на уроках проблемных ситуаций и организации исследовательской деятельности, используя «1С:Урок».
…
Работа с иллюстрациями на уроках химии
Узнайте как использовать иллюстративные материала портала «1С:Урок» на уроках химии.
…
Достижение результатов ФГОС третьего поколения
Как цифровые ресурсы «1С:Урок» помогут в достижении результатов ФГОС третьего поколения: мнение практикующего педагога
…
Вебинар для учителей математики
Узнайте о возможностях портала «1С:Урок» для учителей, репетиторов, учеников и родителей.
…
Работа с интерактивными заданиями по химии портала «1С:Урок»: как использовать редактор химических формул
Рассмотрим возможности редактора химических формул и способы его использования на уроке.
…
Применение теорем Чевы и Менелая при решении задач ЕГЭ
Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.
Задача 1
Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.
Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.
AC = 4 см, AM = 2 см.
Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.
Сторону AP обозначим за y.
Найти: чему равен отрезок AP.
Решение:
Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.
Рассмотрим треугольник ABM. Для него берём прямую OP.
Таким образом мы нашли искомые точки P, A, M, O, K и B.
Запишем теорему Менелая к данному рисунку.
Подставляем в это соотношение известные данные:
В итоге мы получаем, что y = 4.
Ответ: отрезок AP = 4 см.
Задача 2
Задача, связанная со свойствами теоремы Чевы.
Рассмотрим рисунок:
Дано:
-
сумма AB и BC равна 13;
-
AC = 8 см.
Найти: отношение BO и OB1.
Итак, запишем отношение:
Подставляем:
Конечным результатом является дробь 13/8.
Ответ:
https://youtube.com/watch?v=6-icW_4gatM
Доказательство теоремы
Чтобы доказать теорему Менелая, проведем через точку C прямую, параллельную AB, вот так:
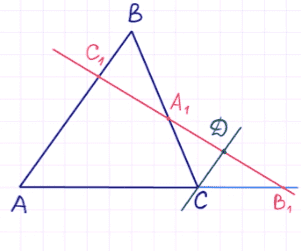
Введите пересечение этой линии с B1C1
через точку Д.
В этом случае мы получим несколько пар подобных треугольников.
Сторона CD параллельна стороне АВ. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они равны по второму признаку равенства треугольников, то есть по двум пропорциональным сторонам и углу В1 между ними.
Углы B1CD и B1AC1 равны для параллельных прямых CD, AB и секущей AC.
Анализируя эту пару подобных треугольников, мы можем записать условие пропорциональности подобных сторон, а именно:
Поскольку сторона CD не входит в исходное равенство, для дальнейшего доказательства ее необходимо выразить.
Используя описанное равенство, используя свойства пропорции, запишем:
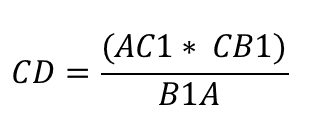
Запишем следующую пару конгруэнтных треугольников: треугольники CDA1 и BC1A1 конгруэнтны, так как углы CA1D и BA1C1 конгруэнтны вертикалям. Кроме того, угол CDA1 равен углу BC1A1, так как он лежит между параллельными прямыми CD, AB и секущей C1D.
Покажем это на картинке:
Из этого подобия можно написать некоторую пропорциональность подобных сторон:
Таким же образом выразим CD:
Остается только сравнить. Дроби, которыми мы выражали CD, те же самые.
Таким образом мы получаем:
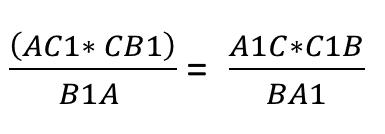
Умножив обе дроби на обратную левой дроби, мы получили исходное равенство:
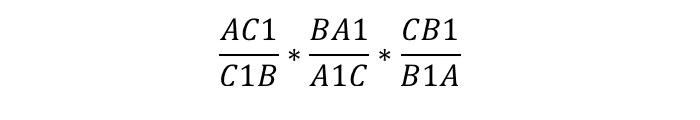
КЭД
Формулировка теоремы Чевы
Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.
Рассматриваемая теорема была доказана ученым в 1678 г.
Рассмотрим приведённый ниже рисунок:
Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:
В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».
Доказательство теоремы
Рассмотрим рисунок:
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.
Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:
Обозначим за O точку пересечения данных прямых.
Продлим медиану BB1.
Проведём перпендикуляры из вершин A и С таким образом:
Запишем соотношение:
Треугольники AKB1 и CNB1 подобны по острому углу.
Аналогично получаем:
Теперь перемножим равенства:
что и требовалось доказать.
Формулировка теоремы Менелая
Менелай Александрийский — древнегреческий математик и астроном, живший в I веке до нашей эры. Он внес большой вклад в развитие сферической тригонометрии, где использовал эту самую теорему, которую теперь изучают все школьники, для получения формул.
Прежде чем приступить к изучению, сделаем подходящий чертеж.
Что у нас есть? Треугольник ABC и прямая, пересекающая две его стороны и продолжение третьей стороны.
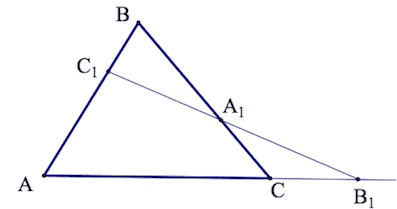
Особенность теоремы заключается в том, что цифра выше чаще всего встречается в заданиях формата ЕГЭ. Это очень распространенная геометрическая конструкция, когда прямая таким образом пересекает треугольник.
Если мы видим рисунок выше, мы можем написать формулу:
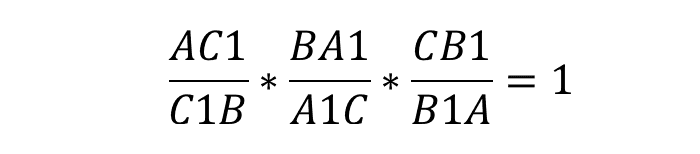
запомнить взаимосвязь просто: действуем по принципу «пик — точка, точка — пик». То есть, если мы получим точку C1 на стороне AB, их отношение запишется следующим образом:
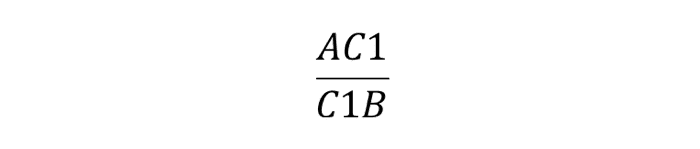
Историческая справка
Менелай Александрийский — древнегреческий астроном и математик. Время его жизни и деятельности определяется двумя астрономическими наблюдениями, приведенными в «Альмагесте» Птолемея, которые Менелай сделал в Риме в первый год правления Траяна, то есть в 98 г. Он является автором работ по сферической тригонометрии: 6 книги по расчету хорд и 3 книги «Сферы».
Джованни Чева — итальянский математик и инженер. Он окончил иезуитский колледж в Милане, после чего стал студентом Пизанского университета, где позже стал профессором математики. С 1686 года Чева работал в Мантуанском университете и оставался на этой должности до конца жизни. Большую часть своей жизни Чева изучал геометрию, пытаясь возродить греческую геометрию; кроме того, сегодня его помнят за его исследования в области механики.
В 1678 г. Чева опубликовал свою знаменитую теорему «О взаимно пересекающихся прямых» по синтетической геометрии треугольника; эта теорема позже получила свое название — теорема Чевы. Эта теорема сегодня является классической теоремой геометрии треугольника. Проще говоря, Чева изобрел некий общий метод, позволяющий с помощью положения точек на сторонах треугольника определять, пересекаются ли соответствующие тройки прямых в одной точке или нет.
В проективной геометрии
В проективной плоскости все прямые секущие. Мы можем построить проективную плоскость, добавив прямую линию, называемую прямой на бесконечности, к аффинной плоскости. Прямые аффинной плоскости одного направления пересекаются в одной и той же точке (иногда называемой несобственной точкой) на этой прямой на бесконечности. В формулировке теоремы отпадает необходимость различать два случая. С другой стороны, отношения алгебраических мер не являются проективными понятиями. Мы можем говорить о поперечном отношении : при построении проективной плоскости, завершенной аффинной плоскостью, поперечное отношение [ A , B , C , D ] равно отношению алгебраической меры [ CA ] к [ CB ], когда D находится на бесконечности. Мы также можем дать версию теоремы в однородных координатах, которые являются продолжением барицентрических координат на проективную плоскость.
Формулировка теоремы Менелая
Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.
Прежде чем приступить к проработке, сделаем соответствующий рисунок.
Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.
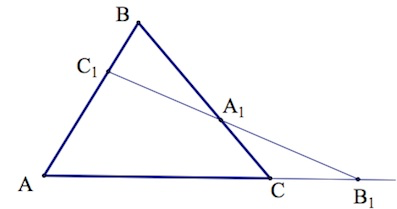
Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.
Если мы видим приведённый выше рисунок, можно записать формулу:
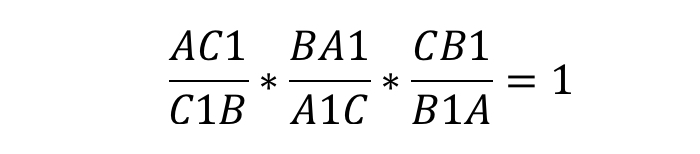
Запомнить отношение просто: действуем по принципу «вершина — точка, точка — вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:
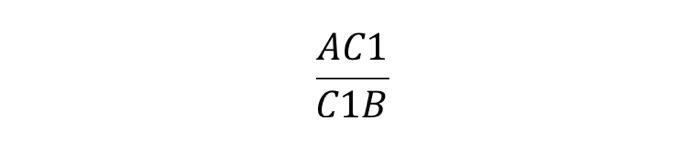
Доказательство теоремы
Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:
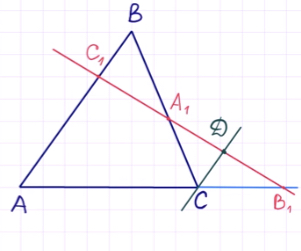
Обозначим точку пересечения данной прямой с B1C1
через точку D.
В таком случае мы получим несколько пар подобных треугольников.
Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B1 между ними.
Углы B1CD и B1AC1 равны как соответственные при параллельных прямых CD, AB и секущей AC.
Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:
Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.
Используя описанное равенства, применив свойства пропорции, запишем:
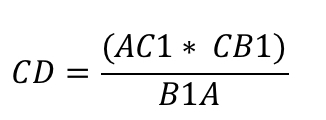
Запишем следующую пару подобных треугольников: треугольники CDA1 и BC1A1 подобны, так как углы CA1D и BA1C1 равны как вертикальные. Кроме этого, угол CDA1 равен углу BC1A1, как накрест лежащие при параллельных прямых CD, AB и секущей C1D.
Покажем это на рисунке:
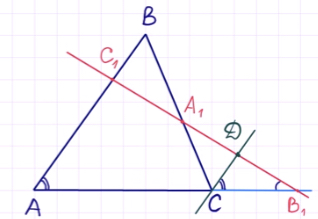
Из данного подобия можно записать некоторую пропорциональность сходственных сторон:
Так же выразим CD:
Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.
Таким образом получаем:
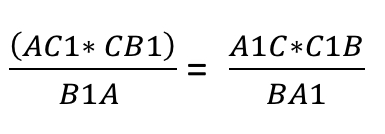
Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:
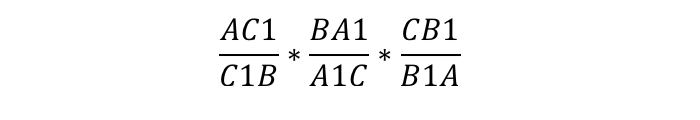
Что и требовалось доказать.
Теорема Чевы и Менелая — формулировка, применение и примеры решения
Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания. Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой
Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.
Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.
Новости
Вебинар для учителей математики
Примите участие в обучающем вебинаре и получите сертификат.
…
Вебинар для учителей обществознания
Примите участие в обучающем вебинаре и получите сертификат.
…
Список ЭОР для рабочей программы учителя математики по обновленному ФГОС
Сохраните подборку цифровых ресурсов по математике и применяйте их на уроках, чтобы сделать занятия современными и интересными для учащихся!
…
Организация исследовательской деятельности на уроках в начальной школе с использованием ЦОР образовательной платформы «1С:Урок»
Опыт создания на уроках проблемных ситуаций и организации исследовательской деятельности, используя «1С:Урок».
…
Работа с иллюстрациями на уроках химии
Узнайте как использовать иллюстративные материала портала «1С:Урок» на уроках химии.
…
Достижение результатов ФГОС третьего поколения
Как цифровые ресурсы «1С:Урок» помогут в достижении результатов ФГОС третьего поколения: мнение практикующего педагога
…
Вебинар для учителей математики
Узнайте о возможностях портала «1С:Урок» для учителей, репетиторов, учеников и родителей.
…
Работа с интерактивными заданиями по химии портала «1С:Урок»: как использовать редактор химических формул
Рассмотрим возможности редактора химических формул и способы его использования на уроке.
…
Слайд 14Заключение Теоремы Чевы и Менелая не изучаются в основном
курсе геометрии 7–9 классов, а лишь в 11 классе. Но
трудности, связанные с освоением этих теорем, оправданы их применением при решении задач. Решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными.Используемая литератураМатематика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.Пособие по геометрии. Часть І. Планиметрия, векторы. В помощь учащимся 10-11-х кл.О.В.Нагорнов, А.В.Баскаков и др.М.:НИЯУ МИФИ,2009.Математика. Подготовка к ЕГЭ. Тематические тесты: геометрия, текстовые задачи. Под ред.Ф.Ф.Лысенко. 2013г.http://hijos.ru/2011/03/16/teorema-chevy/http://www.resolventa.ru/demo/inform/demoinform.htm





























![Math-public:teorema_chevy [президентский фмл №239]](http://rwvt.ru/wp-content/uploads/c/3/3/c33987739e79686c6b713e9faa26e3f6.jpeg)

