Как найти сопряженное значение комплексного числа

Пример сопряженных графов

Сопряженные графы — это пара графов, связанных определенным образом. Один граф называется исходным графом, а другой — его сопряженным графом.

Рассмотрим пример сопряженных графов на простом графе с пятью вершинами:

Исходный граф:

Сопряженный граф:

При сопряжении графов между исходным и сопряженным графами происходит инвертирование ребер. То есть, если в исходном графе вершина A имеет соседние вершины B и C, то в сопряженном графе вершина A становится соседней вершиной для B и C.

В данном примере графы сопряжены вместе, и каждая вершина в исходном графе имеет те же соседние вершины в сопряженном графе, только в обратном порядке. Этот пример наглядно демонстрирует основной принцип сопряжения графов.

Представление комплексных чисел[]

Алгебраическая форма

Запись комплексного числа z{\displaystyle z} в виде x+iy{\displaystyle x+iy}, x,y∈R{\displaystyle x,y\in \mathbb {R} }, называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел может быть вычислена непосредственным суммированием и перемножением таких выражений, с учётом тождества i2=−1{\displaystyle i^{2}=-1}.

Тригонометрическая и показательная формы

Если вещественную x{\displaystyle x} и мнимую y{\displaystyle y} части комплексного числа выразить через модуль r=|z|{\displaystyle r=|z|} и аргумент φ{\displaystyle \varphi } (x=rcos⁡φ{\displaystyle x=r\cos \varphi }, y=rsin⁡φ{\displaystyle y=r\sin \varphi }), то всякое комплексное число z{\displaystyle z}, кроме нуля, можно записать в тригонометрической форме

z=r(cos⁡φ+isin⁡φ){\displaystyle z=r(\cos \varphi +i\sin \varphi )}.

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера

z=reiφ{\displaystyle z=re^{i\varphi }},

где eiφ{\displaystyle e^{i\varphi }} — расширение экспоненты для случая комплексного показателя степени.

Геометрическое представление

Файл:Complex number illustration.svg

Геометрическое представление комплексного числа

Файл:Complex number.svg

Модуль, аргумент, вещественная и мнимая части

Если на плоскости по оси абсцисс расположить действительную часть, а по оси ординат — мнимую, то комплексному числу будет соответствовать точка с декартовыми координатами x{\displaystyle x} и y{\displaystyle y} (или её радиус-вектор, что то же самое), а модуль и аргумент будут полярными координатами этой точки. Такая плоскость называется комплексной.

Отметим, что для пары комплексных чисел z1{\displaystyle z_{1}} и z2{\displaystyle z_{2}} модуль их разности | z1 − z2 |{\displaystyle |~z_{1}~-~z_{2}~|} равен расстоянию между соответствующими точками комплексной плоскости.

Файл:Complex conjugate picture.svg

Геометрическое представление сопряжённых чисел

Сопряжённые комплексные числа получаются зеркальным отражением друг друга относительно вещественной оси.

В геометрическом представлении сумма комплексных чисел соответствует векторной сумме соответствующих векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний.

Формула Муавра

Эта формула позволяет возводить в степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

zn=r(cos⁡φ+isin⁡φ)n=rn(cos⁡nφ+isin⁡nφ){\displaystyle z^{n}=^{n}=r^{n}(\cos n\varphi +i\sin n\varphi )},

где r{\displaystyle r} — модуль, а φ{\displaystyle \varphi } — аргумент комплексного числа.
В современной символике она опубликована Эйлером в 1722 году.

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

z1n=r(cos⁡(φ+2πk)+isin⁡(φ+2πk))1n={\displaystyle z^{1/n}=^{1/n}=}=r1n(cos⁡φ+2πkn+isin⁡φ+2πkn),{\displaystyle =r^{1/n}\left(\cos {\frac {\varphi +2\pi k}{n}}+i\sin {\frac {\varphi +2\pi k}{n}}\right),}k=,1…n−1{\displaystyle \quad k=0,1…n-1}

Отметим, что корни n-ой степени из комплексного числа всегда существуют, и их количество равно n. Геометрически, как видно из формулы, все эти корни располагаются на одной окружности радиуса rn{\displaystyle {\sqrt{r}}}, деля её на n равных частей.

Основные типы задач

В этом разделе будут рассмотрены основные типы простых задач на комплексные числа. Условно задачи на комплексные числа можно разбить на следующие категории.

• Выполнение простейших арифметических операций над комплексными числами.
• Нахождение корней многочленов в комплексных числах.
• Возведение комплексных чисел в степень.
• Извлечение корней из комплексных чисел.
• Применение комплексных чисел для решения прочих задач.

Теперь рассмотрим общие методики решения этих задач.

Выполнение простейших арифметических операций с комплексными числами происходит по правилам описанным в первом разделе, если же комплексные числа представлены в тригонометрической или показательной формах, то в этом случае можно перевести их в алгебраическую форму и производить операции по известным правилам.

Нахождение корней многочленов как правило сводится к нахождению корней квадратного уравнения. Предположим, что у нас есть квадратное уравнение, если его дискриминант неотрицателен, то его корни будут вещественными и находятся по известной формуле. Если же дискриминант отрицателен, то есть D = -1∙a 2
, где a
— некоторое число, то можно представить дискриминант в виде D = (ia) 2
, следовательно √D = i|a|
, а дальше можно воспользоваться уже известной формулой для корней квадратного уравнения.

Пример
. Вернемся к упомянутому выше квадратному уравнению x 2 + x + 1 = 0
.
Дискриминант — D = 1 — 4 ∙ 1 = -3 = -1(√3) 2 = (i√3) 2
.
Теперь с легкостью найдем корни: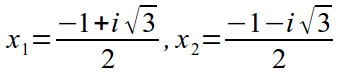

Возведение комплексных чисел в степень можно выполнять несколькими способами. Если требуется возвести комплексное число в алгебраической форме в небольшую степень (2 или 3), то можно сделать это непосредственным перемножением, но если степень больше (в задачах она часто бывает гораздо больше), то нужно записать это число в тригонометрической или показательной формах и воспользоваться уже известными методами.

Пример
. Рассмотрим z = 1 + i
и возведем в десятую степень.
Запишем z
в показательной форме: z = √2 e iπ/4
.
Тогда z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4
.
Вернемся к алгебраической форме: z 10 = -32i
.

Извлечение корней из комплексных чисел является обратной операцией по отношению к операции возведения в степень, поэтому производится аналогичным образом. Для извлечения корней довольно часто используется показательная форма записи числа.

Пример
. Найдем все корни степени 3
из единицы. Для этого найдем все корни уравнения z 3 = 1
, корни будем искать в показательной форме.
Подставим в уравнение: r 3 e 3iφ = 1 или r 3 e 3iφ = e 0 .
Отсюда: r = 1
, 3φ = 0 + 2πk
, следовательно φ = 2πk/3
.
Различные корни получаются при φ = 0, 2π/3, 4π/3
.
Следовательно 1
, e i2π/3
, e i4π/3
— корни.
Или в алгебраической форме: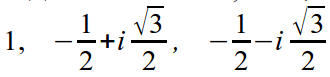

Последний тип задач включается в себя огромное множество задач и нет общих методов их решения. Приведем простой пример такой задачи:

Хоть в формулировке этой задачи и не идет речь о комплексных числах, но с их помощью ее можно легко решить. Для ее решения используются следующие представления: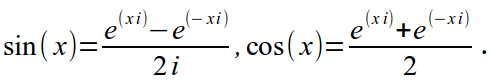
Если теперь подставить это представление в сумму, то задача сводится к суммированию обычной геометрической прогрессии.

Заключение

Комплексные числа широко применяются в математике, в этой обзорной статье были рассмотрены основные операции над комплексным числами, описаны несколько типов стандартных задач и кратко описаны общие методы их решения, для более подробного изучения возможностей комплексных чисел рекомендуется использовать специализированную литературу.

§ 1. Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа (Сформулируйте определение комплексного числа)

Комплексным числомz называется выражение следующего вида:

Комплексное число в алгебраической форме,(1)

Где x, y

Î;

— комплексно сопряженное число
числу z

;

— противоположное число
числу z

;

— комплексный ноль
;

– так обозначается множество комплексных чисел.

1)z

= 1 + i

Þ Re z

= 1, Im z

= 1, = 1 – i,

= –1 – i

;

2)z

= –1 + i

Þ Re z

= –1, Im z

= , = –1 – i,

= –1 –i

;

3)z

= 5 + 0i

= 5 Þ Re z

= 5, Im z

= 0, = 5 – 0i

= 5, = –5 – 0i

= –5

Þ если Imz

= 0, то z

= x

— действительное число;

4)z

= 0 + 3i

= 3i

Þ Re z

= 0, Im z

= 3, = 0 – 3i

= –3i

, = –0 – 3i

= – 3i

Þ если Rez

= 0, то z

= iy

— чисто мнимое число
.

Комплексные равенства
(Сформулируйте смысл комплексного равенства)

1) ;

2) .

Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.

1) ;

2) .

Комплексное число z

изображается точкой (x

, y
) на комплексной плоскости или радиус-вектором этой точки.

Знак z

во второй четверти означает, что система декартовых координат будет использоваться как комплексная плоскость.

Модуль и аргумент комплексного числа
(Что такое модуль и аргумент комплексного числа?)

Модулем комплексного числа называется неотрицательное действительное число

.(2)

Геометрически модуль комплексного числа — это длина вектора, изображающего число z

, или полярный радиус точки (x

, y
).

Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.

1)z

= 1 + i

Þ

,

Þ

Þ;

,

Þ

Þ;

,

5),

то есть для z = 0 будет

, j

не определен.

Арифметические действия над комплексными числами
(Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.)

Сложение (вычитание) комплексных чисел

z

1 ±z

2 = (x

1 + iy

1) ± (x

2 + iy

2) = (x

1 ±x

2) + i

(y

1 ±y

2),(5)

то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.

1)(1 + i
) + (2 – 3i
) = 1 + i

+ 2 –3i

= 3 – 2i

;

2)(1 + 2i
) – (2 – 5i
) = 1 + 2i

– 2 + 5i

= –1 + 7i

.

1)z

1 + z

2 = z

2 + z

1;

2)z

1 + z

2 + z

3 = (z

1 + z

2) + z

3 = z

1 + (z

2 + z

3);

3)z

1 – z

2 = z

1 + (– z

2);

4)z

+ (–z
) = 0;

Умножение комплексных чисел в алгебраической форме

z

1∙z

2 = (x

1 + iy

1)∙(x

2 + iy

2) = x

1x

2 + x

1iy

2 + iy

1x

2 + i

2y

1y

2 = (6)

= (x

1x

2 – y

1y

2) + i

(x

1y

2 + y

1x

2),

то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой и приведением подобных по действительным и мнимым слагаемым.

1)(1 + i
)∙(2 – 3i
) = 2 – 3i

+ 2i

– 3i

2 = 2 – 3i

+ 2i

+ 3 = 5 – i

;

2)(1 + 4i
)∙(1 – 4i
) = 1 – 42 i

2 = 1 + 16 = 17;

3)(2 + i
)2 = 22 + 4i

+ i

2 = 3 + 4i

.

Умножение комплексных чисел тригонометрической форме

z

1∙z

2 = r

1(cosj

1 + i

sinj

1)×r

2(cosj

2 + i

sinj

2) =

= r

1r

2(cosj

1cosj

2 + i

cosj

1sinj

2 + i

sinj

1cosj

2 + i

2 sinj

1sinj

2) =

= r

1r

2((cosj

1cosj

2 – sinj

1sinj

2) + i

(cosj

1sinj

2 + sinj

1cosj

2))

Произведение комплексных чисел в тригонометрической форме, то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.

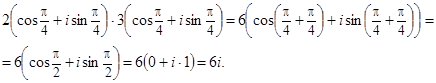
Основные свойства умножения

1)z

1×z

2 = z

2×z

1 — коммутативность;

2)z

1×z

2×z

3 = (z

1×z

2)×z

3 = z

1×(z

2×z

3) — ассоциативность;

3)z

1×(z

2 + z

3) = z

1×z

2 + z

1×z

3 — дистрибутивность относительно сложения;

4)z

×0 = 0; z

×1 = z

;

Деление комплексных чисел

Деление — это обратная умножению операция, поэтому

если z

×z

2 = z

1 и z

2 ¹ 0, то .

При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:

Деление комплексных чисел в алгебраической форме.(7)

При выполнении деления в тригонометрической форме модули делятся, а аргументы вычитаются:

Деление комплексных чисел в тригонометрической форме.(8)

2).

Возведение комплексного числа в натуральную степень

Возведение в натуральную степень удобнее выполнять в тригонометрической форме:

Формула Муавра,(9)

то есть при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на показатель степени.

Вычислить (1 + i
)10.

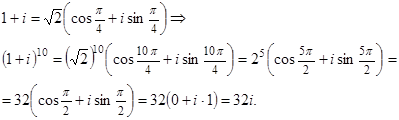
Замечания

1. При выполнении операций умножения и возведения в натуральную степень в тригонометрической форме могут получаться значения углов за пределами одного полного оборота. Но их всегда можно свести к углам или сбрасыванием целого числа полных оборотов по свойствам периодичности функций и .

2. Значение называют главным значением аргумента комплексного числа ;

при этом значения всех возможных углов обозначают ;

очевидно, что , .

Извлечение корня натуральной степени из комплексного числа

Формулы Эйлера(16)

по которым тригонометрические функции и действительной переменной выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.

Краткая вводная

Когда-то нам хватало натуральных чисел:

\

Всё было прекрасно: «У тебя 5 бананов, у меня ещё 3 — итого у нас 5 + 3 = 8 бананов». Сумма двух натуральных чисел всегда даёт новое натуральное число (говорят, что операция сложения замкнута на множестве натуральных чисел).

Но вот на сцену выходит вычитание — и натуральных чисел стало недостаточно. Например разность 3 − 5 = −2 уже не будет натуральным. Так появились целые числа (натуральные, им противоположные и ноль):

\

Дальше к делу подключились операции умножения и деления. Да, произведение двух целых чисел всё ещё целое, но вот деление приводит к образованию дробей. Например, 1 : 2 или 5 : 4 уже нельзя записать целым числом. Так появилось множество рациональных чисел или множество дробей:

\

Это был настоящий триумф для древней математики, и в тот момент казалось, что ничего больше уже изобрести нельзя. Да и зачем?

Проблема пришла откуда не ждали. В какой-то момент классическое умножение «разрослось» до возведения в степень:

\

Тут-то и выяснилось, что возведение рационального числа в натуральную степень всё ещё будет рациональным числом. Но вот обратная операция — извлечение корня — выносит нас за пределы рациональных чисел:

\

Так появилось множество действительных чисел — множество бесконечных десятичных дробей, которые могут быть периодическими (и тогда это обычное рациональное число) и непериодическими (такие числа называют иррациональными, и их неизмеримо больше).

\

Казалось бы: ну вот теперь точно всё! Что ещё нужно для счастья? Проблема в том, что на множестве действительных чисел нельзя извлечь даже самый простой квадратный корень из отрицательного числа:

\

Однако законы физики (особенно электродинамика и вообще всё, где есть слово «динамика») как бы намекали, что множество содержательных процессов протекает там, где привычные корни не извлекаются. А значит, следует расширить множество действительных чисел так, чтобы такие корни всё же извлекать.

И тут открылись врата в Ад…