Сложение, умножение и деление комплексных чисел. сопряжённые числа

Примеры

Лучший способ понять теорию — посмотреть на достаточное количество примеров. Это то, что мы собираемся сделать.

Все наши примеры будут связаны с операцией умножения, потому что она самая интересная.

Умножение на нуль

Если модуль одного из аргументов равен нулю, модуль результата также будет равен нулю при умножении. В результате получаем известное тождество

Умножение на действительное число

Я уже говорил, что умножение на комплексное число рождает сразу два эффекта: вращение и растяжение. Мы можем получить каждый из этих эффектов отдельно.

Например, умножение любого числа X на действительное число Y (аргумент равен 0) просто увеличивает число X в Y раз. И мы получаем операцию растяжения без вращения.

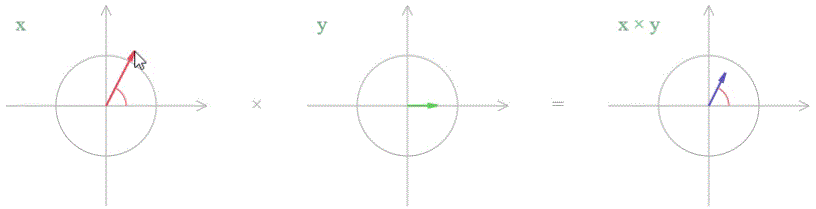
синий вектор имеет то же направление, что и красный, но другую длину синий вектор имеет то же направление, что и красный, но другую длину

Умножение на число единичной длины

Наоборот, мы можем получить операцию поворота без растяжения, если умножим число X на комплексное число Y единичной длины. Тогда число X просто поворачивается на угол, равный аргументу числа Y.

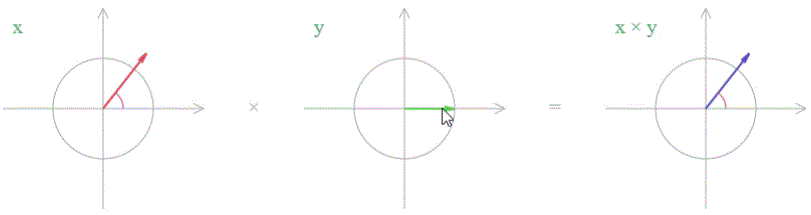
синий вектор имеет ту же длину, что и красный вектор, но повернут относительно него на угол, заданный зеленым вектором

Умножение на мнимую единицу

Умножение на воображаемую единицу дает поворот на 90 градусов.

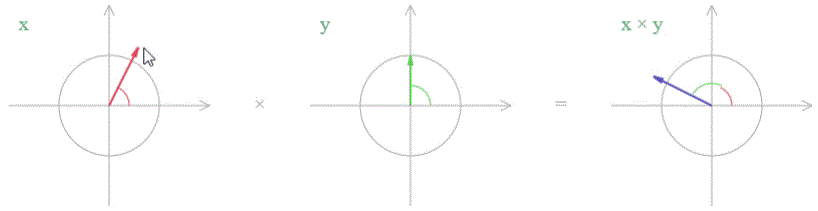
синий вектор повернут на 90 градусов против часовой стрелки относительно красного вектора синий вектор повернут на 90 градусов против часовой стрелки относительно красного

А умножение на минус мнимой единицы дает поворот на 90 градусов в противоположном направлении.

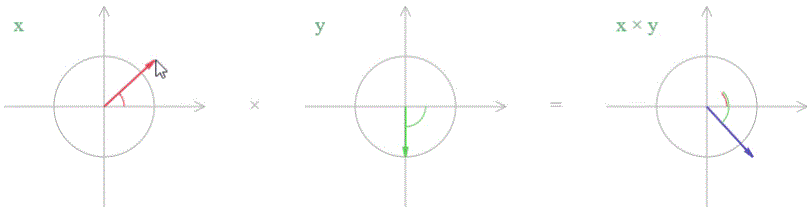
синий вектор повернут на 90 градусов по часовой стрелке относительно красного вектора синий вектор повернут на 90 градусов по часовой стрелке относительно красного вектора

Умножение на действительную единицу

Самый банальный вариант — умножение на действительную единицу. Нам нужно повернуть фигуру X на нулевой угол и растянуть ее 1 раз. Другими словами, мы получим число X без изменений.

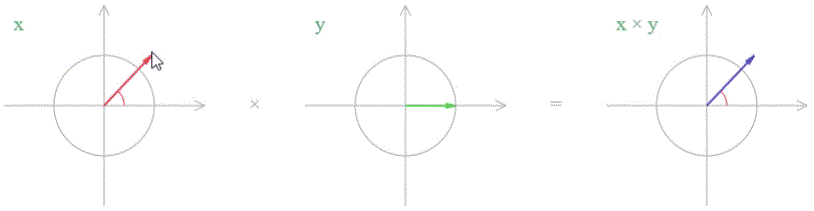
синий вектор равен красному синий вектор равен красному

Это именно то, к чему мы привыкли со школы. Умножение любого числа на единицу должно дать одно и то же число.

Умножение мнимой единицы на мнимую единицу

Аргумент мнимой единицы равен 90 градусам, а модуль равен единице. Это означает, что когда мы возводим воображаемую единицу в квадрат, мы получаем количество единиц длины, повернутых на 180 градусов. А именно -1.

квадрат мнимой единицы равен -1 квадрат мнимой единицы равен -1

Мы также уже знаем это свойство, потому что приняли его за определение мнимой единицы

определение воображаемой единицы определение воображаемой единицы

Умножение отрицательного действительного числа на положительное действительное число

Отрицательное число имеет аргумент 180 градусов. А положительный — аргумент 0. При умножении аргументы складываются и получается угол 180 градусов. В результате снова получается отрицательное число.

минус раз плюс дает минус минус раз плюс дает минус

Это правило известно нам как «минус, умноженный на плюс, дает минус».

Умножение двух отрицательных действительных чисел

Когда мы добавляем аргументы к двум отрицательным числам (два раза по 180), мы получаем полный поворот на 360 градусов. Результат — положительное число.

минус раз минус дает плюс минус раз минус дает плюс

И мы знаем это правило как «минус, умноженный на минус, дает плюс».

Мне очень интересно, как вышеуказанные правила выражаются через добавление углов :).

Понятие бесконечности на множестве комплексных чисел

Как и в реальной области, на множестве комплексных чисел вводится понятие бесконечности, бесконечно удаленной точки. Это можно сделать по аналогии с набором действительных чисел по геометрическим причинам.

Рассмотрим числовую прямую и круг, соприкасающиеся с линией в точке; будет указана точка, диаметрально противоположная точке.

Соединим разные точки оси точкой с прямыми линиями; точки пересечения прямых с кругом будут обозначены значком. Очевидно, каждая точка соответствует точке. Обратное верно для всех точек в круге, кроме точки. Но когда вы удаляетесь по прямой от точки (с увеличением расстояния, равным), ее изображение на окружности приближается к точке.

Для такой последовательности в анализе принято бесконечно большое имя (значение) последовательности. Ее предел обозначается и называется бесконечностью или бесконечно удаленной точкой. Следовательно, точку можно рассматривать как изображение бесконечно удаленной точки на окружности, а бесконечность — как «точку» оси, изображение которой на окружности является точкой .

По аналогии рассмотрим плоскость (плоскость) и касательную к ней сферу в начале координат, т.е в точке (рис. 1.2, а). Лучи, соединяющие точки с точкой, пересекают сферу в точках. В этом случае одна точка соответствует любой точке, и наоборот, одна точка соответствует любой точке. Очевидно, что чем дальше точка от начала координат (это длина радиус-вектора точки), тем ближе ее изображение к точке. Чтобы совпадение было полным, вводится «несоответствующий» элемент (символ), бесконечно удаленная точка, такая как точка на плоскости, изображение которой находится на этой точке .

Плоскость, объединенная элементом, называется расширенной комплексной плоскостью и обозначается значком .

Однозначное соответствие, построенное между точками сферы и целым, называется стереографической проекцией, а сфера — сферой Римана.

Разновидности формул умножения в зависимости от формы записи

Благодаря наличию специальных формул, можно оперативно выполнять различные операции с комплексными числами, включая примеры из тригонометрии. Теоретический порядок действий при умножении зависит от того, в какой форме записано комплексное число.

Формула умножения в алгебраической форме

В данном случае для того чтобы умножить комплексные числа, необходимо перемножить их компоненты, поочередно раскрывая скобки, согласно формуле. При этом следует учитывать, что (i^2 = -1).

В итоге получим:

(z_1 cdot z_2 = (x_1+y_1i) cdot (x_2 + y_2i) = (x_1 cdot x_2 — y_1 cdot y_2) + (x_1 cdot y_2 + x_2 cdot y_1)i)

Формула умножения в показательной форме

Если требуется найти произведение комплексных чисел, которые записаны в показательной форме, то целесообразно воспользоваться способом прямого перемножения всех элементов:

(z_1 cdot z_2 = r_1e^{varphi_1 i} cdot r_2e^{varphi_2 i} = r_1cdot r_2 cdot e^{(varphi_1+varphi_2)i})

Формула умножения в тригонометрической форме

Найти произведение комплексных чисел, записанных с помощью тригонометрической формы, можно, таким образом:

(z_1 cdot z_2 = r_1 cdot r_2 cdot (cos(varphi_1+varphi_2) + isin(varphi_1+varphi_2)))

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

• целые числа;
• дроби;
• иррациональные числа.

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. z = a + bi

z = a + bi

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

• a — действительная часть (Re z) комплексного числа z;
• b — мнимая часть (Im z) комплексного числа z.

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

z = bi + a

Мнимую единицу допускается переставлять:

z = a + ib

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

z = a + bi

Определение

Комплексным числом называют выражение a + bi, в котором а и b являются действительными числами, i представляет собой мнимую единицу, символ, квадрат которого равен -1, то есть i2=-1. Число а представляет собой действительную часть, b — мнимую часть комплексного числа z = a + bi. Если b = 0, то вместо a + 0i записывают a. Действительные числа являются частным случаем комплексных чисел.

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

• ноль;
• единицу для действительной оси;
• мнимую единицу i для мнимо оси.

С помощью комплексной плоскости можно построить заданные комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Можно рассмотреть следующие комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

Есть ряд чисел с ненулевыми действительной и мнимой частью:

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Алгебраическая форма записи комплексных чисел

Пусть x и y — произвольные действительные числа.

Множеством комплексных чисел называется множество всех возможных пар (x, y) действительных чисел, где операции сложения, вычитания и умножения определены в соответствии с описанными ниже правилами.

Множество комплексных чисел является расширением множества действительных чисел, так как множество действительных чисел содержится в нем в виде пар (x, 0).

Комплексные числа, заданные парами (0, y), называются чисто мнимыми числами.

Для комплексных чисел существует несколько форм записи: алгебраическая запись, тригонометрическая запись и экспоненциальная (экспоненциальная) запись.

Алгебраическая форма — это форма записи комплексных чисел, в которой комплексное число z, заданное парой действительных чисел (x, y), записывается как

где используется символ i, называемый мнимой единицей.

Число x называется действительной (вещественной) частью комплексного числа z = x + iy и обозначается Re z.

Число y называется мнимой частью комплексного числа z = x + iy и обозначается Im z.

Комплексные числа с Im z = 0 являются действительными числами.

Комплексные числа с Re z = 0 — чисто мнимые числа.

Тригонометрическая и экспоненциальная формы записи комплексных чисел будут рассмотрены чуть позже.

Деление комплексных чисел

Пример 4

Даны комплексные числа 

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу 

знаменатель

Согласно правилу, знаменатель нужно умножить на  , и, чтобы ничего не изменилось, домножить числитель на то же самое число  :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой   (помним, что  и не путаемся в знаках!!!).

Распишу подробно:

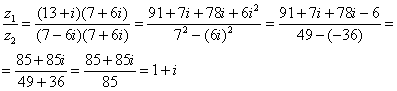
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде 

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: 

Редко, но встречается такое задание:

Пример 5

Дано комплексное число 

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу  . В знаменателе уже есть  , поэтому знаменатель и числитель нужно домножить на сопряженное выражение  , то есть на 

Пример 6

Даны два комплексных числа 

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Что такое комплексные числа и их умножение

В математических науках часто применяют при решении задач не только натуральные, рациональные и вещественные числа, но и комплексные.

Определение

Комплексное число — это отдельный вид чисел, который представлен множеством, обозначаемым с помощью символа \(\mathbb{C}\).

Рассмотреть комплексное число можно на доказательстве примера. Если записать обычное множество в виде z = a + ib, то под мнимой единицей будет подразумеваться выражение \(i = \sqrt{-1}\). Числа \(a,b \in \mathbb{R}\) являются вещественными числами.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

В том случае, когда b = 0, комплексное число трансформируется в вещественное число. Исходя из этого, можно сделать вывод, что действительные числа являются частным случаем комплексных чисел. Запись данного заключения будет иметь следующий вид подмножества:

\(\mathbb{R} \subset \mathbb{C}\)

Следует отметить, что также допустимо равенство:

a = 0

Согласно принятым правилам, мнимая часть комплексного числа записывается в виде:

Im(z) = b

Действительная часть комплексного числа представляет собой выражение:

Re(z) = a

Рассмотрев множество на примере, можно представить формулировку комплексно-сопряженных чисел.

Определение

Каждое комплексное число z = a+ib предполагает наличие такого числа, называемого сопряженным, при котором \(\overline{z} = a-ib\).

Разница между записанными числами заключается в неодинаковых знаках перед действительным и мнимым компонентом чисел.

В математической науке для данных чисел предусмотрено несколько форм. Таким образом, одинаковые числа достаточно просто записать разными методами:

1. Алгебраическая форма: \(z = a+ib\).
2. Показательная форма: \(z = |z|e^{i\varphi}\).
3. Тригонометрическая форма: \(z = |z|\cdot(\cos(\varphi)+i\sin(\varphi))\).

С помощью несложных манипуляций одну форму числа можно перевести в другой вариант записи. Алгебраическая запись является более распространенной. Однако допустимо изображать комплексные числа на плоскости. В итоге получим числа \(a,b \in \mathbb{R}\) расположенные на соответствующих осях плоскости.

Комплексное число z = a+ib можно представить в качестве вектора \(\overline{z}\). При этом для обозначения аргумента можно использовать запись \(\varphi\). При определении модуля |z| используют длину вектора \(\overline{z}\) и соответствующую формулу:

\(|z| = \sqrt{a^2+b^2}\)

С помощью различных уравнений, выбор которых определяется полуплоскостью, в котором расположено само число, определяют аргумент комплексного числа \(\varphi\).

Справедливы следующие закономерности:

1. a>0, то \(\varphi = arctg\frac{b}{a}\).
2. a<0, b>0, то \(\varphi = \pi + arctg\frac{b}{a}\).
3. a<0, b<0, то \(\varphi = -\pi + arctg\frac{b}{a}\).

Умножить комплексные числа в алгебраической форме можно, таким образом:

\(z_1 \cdot z_2 = (a_1+ib_1) \cdot (a_2+ib_2) = (a_1 a_2 — b_1 b_2)+i(a_1 b_2 + a_2 b_1)\)

Операция умножения комплексных чисел, записанных в показательном варианте, имеет следующий вид:

\(z_1 \cdot z_2 = |z_1|e^{i\varphi_1} \cdot |z_2|e^{i\varphi_2} = |z_1|\cdot|z_2|\cdot e^{i(\varphi_1 + \varphi_2)}\)

Умножение комплексных чисел в геометрической форме

Если комплексные числа $z_{1}$ и
$z_{2}$ заданы в
геометрической форме:
$z_{1}=left|z_{1}right|left(cos phi_{1}+i sin phi_{1}right)$,
$z_{2}=left|z_{2}right|left(cos phi_{2}+i sin phi_{2}right)$, то произведением этих чисел есть число

$z_{1} z_{2}=left|z_{1}right| cdotleft|z_{2}right|left$

То есть модуль произведения двух комплексных чисел в тригонометрической форме равен произведению
модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти произведение чисел $z_{1}=3 cdotleft(cos 10^{circ}+i sin 10^{circ}right)$, $z_{2}=2 cdotleft(cos 50^{circ}+i sin 50^{circ}right)$ .

Решение. Модуль произведения равен $|z|=3 cdot 2=6$, а аргумент $phi=10^{circ}+50^{circ}=60^{circ}$, а тогда искомое число в тригонометрической форме имеет вид:

$z=|z|(cos phi+i sin phi)=6 cdotleft(cos 60^{circ}+i sin 60^{circ}right)$

Запишем результат в алгебраической форме, для этого вычислим значения соответствующих тригонометрических функций, будем в результате иметь:

$z=6 cdotleft(frac{1}{2}+i cdot frac{sqrt{3}}{2}right)=3+3 sqrt{3} i$

Ответ. $z=6 cdotleft(cos 60^{circ}+i sin 60^{circ}right)=3+3 sqrt{3} i$

Примеры решения задач

Задача 1

Задача

Необходимо найти частное пары комплексных чисел:

(z_1 = 3+i) и (z_2 = 2-3i)

Решение:

Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.

(frac{z_1}{z_2} = frac{3+i}{2-3i} =)

Сопряженное комплексное число к знаменателю:

(overline{z_2} = 2+3i)

Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:

(= frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =)

Далее следует привести подобные слагаемые и записать вывод с ответом:

(= frac{3 + 11i}{13} = frac{3}{13} + frac{11}{13}i)

Ответ: (frac{z_1}{z_2} = frac{3}{13} + frac{11}{13}i)

Задача 2

Задача

Требуется выполнить деление комплексных чисел:

(z_1 = 2(cos frac{pi}{3} + isin frac{pi}{6}))

(z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6}))

Решение:

Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:

Деление модулей:

(frac{r_1}{r_2} = frac{2}{4} = frac{1}{2})

Разность аргументов:

(varphi_1 — varphi_2 = frac{pi}{3} — frac{pi}{6} = frac{pi}{6})

Следующим шагом является деление чисел:

(frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Ответ: (frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Задача 3

Задача

Нужно найти частное комплексных чисел:

(z_1 = 3e^{frac{pi}{2}i})

(z_2 = 4e^{frac{pi}{4}i})

Решение:  Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:

(frac{r_1}{r_2} = frac{3}{4})

(varphi_1 — varphi_2 = frac{pi}{2} — frac{pi}{4} = frac{pi}{4})

При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:

(frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Ответ: (frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Задача 4

Задача

Определить частное:

(frac{-2+i}{1-i})

Решение:

В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:

(1-i)

Данным числом является:

(1+i)

Таким образом:

(frac{-2+i}{1-i}=frac{-2+i}{1-i} cdot frac{1+i}{1+i}=frac{(-2+i)(1+i)}{(1-i)(1+i)})

Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:

(i^{2}=-1)

(frac{-2+i}{1-i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}=frac{-2-2 i+i-1}{1^{2}-i^{2}}=)

(=frac{-3-i}{1-(-1)}=frac{-3-i}{2}=-frac{3}{2}-frac{i}{2})

Ответ:( frac{-2+i}{1-i}=-frac{3}{2}-frac{i}{2})

Задача 5

Задача

Необходимо найти частное:

(frac{z_{1}}{z_{2}})

При условии, что:

(z_{1}=2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right))

(z_{2}=cos frac{pi}{4}+i sin frac{pi}{4})

Решение:

Искомое частное:

(frac{z_{1}}{z_{2}}=frac{2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)}{cos frac{pi}{4}+i sin frac{pi}{4}}=)

(=frac{2}{1} cdotleft=)

(=2 cdotleft=2 cdot(0+i)=2 i)

Ответ: (frac{z_{1}}{z_{2}}=2 cdotleft(cos frac{pi}{2}+i sin frac{pi}{2}right)=2 i)

Задача 6

Задача

Необходимо разделить два комплексных числа:

(z_{1}=-1+3i)

(z_{2}=1+2i)

Решение:

С помощью соответствующей формулы можно записать уравнение:

(z_{1} div z_{2} = frac{-1+3i}{1+2i} = frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = frac{-1 cdot 1 + 3 cdot 2}{1^{2}+2^{2}} + i frac{3 cdot 1 + (-1) cdot (-2)}{1^{2}+2^{2}} =)

(= frac{5}{5} + i frac{5}{5}=1+i)

Ответ: ( z_{1} div z_{2} = 1+i)

Задача 7

Задача

Необходимо вычислить частное комплексных чисел:

(z_{1}=sqrt{2} left( cos frac{pi}{2} + i sin frac{pi}{2} right))

(z_{2}=sqrt{2} left( cos frac{pi}{4} + i sin frac{pi}{4} right))

Решение:

Используя соответствующую формулу, запишем:

(z_{1} div z_{2} = frac{r_{1}}{r_{2}} (cos ( varphi _{1} — varphi _{2}) + i sin ( varphi _{1} — varphi _{2})) = frac{sqrt{2}}{sqrt{2}} left( cos left( frac{pi}{2}-frac{pi}{4} right) + i sin left( frac{pi}{2}-frac{pi}{4} right) right) =)

(= 1 cdot left( cos frac{pi}{4} + i sin frac{pi}{4} right) = cos frac{pi}{4} + i sin frac{pi}{4})

Ответ:( z_{1} div z_{2} = cos frac{pi}{4} + i sin frac{pi}{4})

Задача 8

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №39. Геометрическая интерпретация комплексного числа.

Перечень вопросов, рассматриваемых в теме

1. изображение комплексного числа на плоскости- точками;
2. изображение комплексного числа на плоскости- векторами;

3) определение модуля комплексного числа.

Глоссарий по теме:

а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M (a; b)

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Геометрическое изображение комплексных чисел.

а) Комплексные числа изображаются точками плоскости по следующему правилу: a + bi = M (a; b) (рис.1).

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).

Пример. Постройте точки, изображающие комплексные числа: 1; — i; — 1 + i; 2 – 3i (рис.3).

Модуль комплексного числа

Как отмечалось выше, комплексное число также можно изображать радиус-вектором (рис. 4).

Длина радиус-вектора, изображающего комплексное число z=a+bi, называется модулем этого комплексного числа.

Модуль любого ненулевого комплексного числа есть положительное число. Модули комплексно сопряженных чисел равны. Модуль произведения/частного двух комплексных чисел равен произведению/частному модулей каждого из чисел.

Модуль вычисляется по формуле:

То есть модуль есть сумма квадратов действительной и мнимой частей заданного числа.

Иногда еще модуль комплексного числа обозначается как r или ρ.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Найдите модуль комплексного числа z=5-3i

1. 4
2. 5

Решим данное задание, используя определение модуля.

Т.к. Re z=5, Im z= -3, то искомое значение

Верный ответ: 2.

№2. Тип задания: рисование.

Изобразите вектором на комплексной плоскости точку z=2+3i

Разобьем z=2+3i на две части: z₁=2 и z₂= 3i. Отметим на плоскости точки О и А, соединим их:

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Свойство операции умножения

Операция умножения обладает следующим неочевидным свойством.

Это означает, что при перемножении двух чисел их аргументы (углы) складываются, а длина умножается.

Посмотрите еще раз внимательно на умножение. Я специально пометил вершины, чтобы было видно, что при умножении вершины действительно складываются.

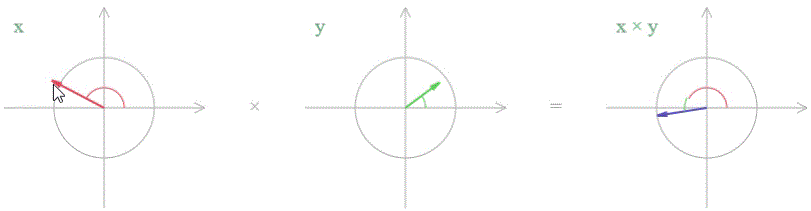
Допустим, у нас есть число X. Когда мы умножаем его на другое число Y, мы, таким образом, расширяем число X до |Y| раз и повернуть на угол Arg(Y).

Кстати, операции поворота и растяжения коммутируют друг с другом

Им неважно, в каком порядке мы их выполняем. Они как бы бегут одновременно

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

Сложение
комплексных чисел

Для
того чтобы сложить два комплексных
числа нужно сложить их действительные
и мнимые части:

z 1
+ z 2
= (a 1
+ a 2)
+ i*(b 1
+ b 2).

Для
комплексных чисел справедливо правило
первого класса: z 1
+ z 2
= z 2
+ z 1
–
от перестановки слагаемых сумма не
меняется.

Вычитание
комплексных чисел

Действие
аналогично сложению, единственная
особенность состоит в том, что вычитаемое
нужно взять в скобки, а затем – стандартно
раскрыть эти скобки со сменой знака:

z 1
+ z 2
= (a 1
– a 2)
+ i*(b 1
– b 2)

Умножение
комплексных чисел

Основное
равенство комплексных чисел:

Произведение
комплексных
чисел:

z 1
* z 2
= (a 1
+ i*b 1)*(a 2
+ i*b 2)
= a 1 *a 2
+ a 1 *i*b 2
+ a 2 *i*b 1
+ i 2 *b 1 *b 2
= a 1 *a 2
— b 1 *b 2
+i*(a 1 *b 2
+a 2 *b 1).

Как
и сумма, произведение комплексных чисел
перестановочно, то есть справедливо
равенство: .

Деление
комплексных чисел

Деление
чисел осуществляется методом
умножения знаменателя и числителя на
сопряженное знаменателю выражение
.

В какую сторону отмерять углы?

Есть некоторая неоднозначность в измерении углов. Например, числовой аргумент на изображении равен -45 градусов. Но мы могли бы также сказать, что угол +315 градусов.

числовой аргумент равен -45 или +315 числовой аргумент равен -45 или +315

Хитрость в том, что для операции умножения не имеет значения, как мы измеряем углы.

Например, когда мы умножаем два числа единичной длины на аргумент -45, мы получаем угол -90 градусов. Таким образом, мы получаем число, равное минус мнимое.

Если отложить углы в обратную сторону и считать, что аргументы этих чисел не -45, а +315. Итак, когда мы складываем углы, мы получаем +630. Это то же самое, что -90. И снова получаем минус мнимой единицы.

Хотя у нас есть некоторая неопределенность в измерении углов, это никак не влияет на результат операции умножения. Умножение совершенно уникально.