Таблица арктангенсов и арккотангенсов на окружности

Теоремы сложения

→ Основная статья :

Теоремы сложения для арктангенса и арккотангенса получены с помощью :

арктан⁡Икс+арктан⁡узнак равно{арктан⁡(загар⁡(арктан⁡Икс+арктан⁡у))знак равноарктан⁡(Икс+у1-Иксу)если Иксу<1π+арктан⁡(загар⁡(арктан⁡Икс+арктан⁡у))знак равноπ+арктан⁡(Икс+у1-Иксу)если Икс+у≥ а также Иксу>1-π+арктан⁡(загар⁡(арктан⁡Икс+арктан⁡у))знак равно-π+арктан⁡(Икс+у1-Иксу)если Икс+у< а также Иксу>1{\ displaystyle \ arctan x + \ arctan y = \ left \ {{\ begin {matrix} \ arctan (\ tan (\ arctan x + \ arctan y)) = \ arctan \ left ({\ frac {x + y}) {1 -xy}} \ right) & {\ text {if}} xy <1 \\\ pi + \ arctan (\ tan (\ arctan x + \ arctan y)) = \ pi + \ arctan \ left ({ \ frac {x + y} {1-xy}} \ right) & {\ text {if}} x + y \ geq 0 {\ text {and}} xy> 1 \\ — \ pi + \ arctan (\ tan (\ arctan x + \ arctan y)) = — \ pi + \ arctan \ left ({\ frac {x + y} {1-xy}} \ right) & {\ text {if}} x + y < 0 {\ text {and}} xy> 1 \\\ end {matrix}} \ right.}

арккот⁡Икс+арккот⁡узнак равно{арккот⁡(детская кроватка⁡(арккот⁡Икс+арккот⁡у))знак равноарккот⁡(Иксу-1Икс+у)если Икс+у>π+арккот⁡(детская кроватка⁡(арккот⁡Икс+арккот⁡у))знак равноπ+арккот⁡(Иксу-1Икс+у)если Икс+у<{\ displaystyle \ operatorname {arccot} x + \ operatorname {arccot} y = \ left \ {{\ begin {matrix} \ operatorname {arccot} (\ cot (\ operatorname {arccot} x + \ operatorname {arccot} y) ) = \ operatorname {arccot} \ left ({\ frac {xy-1} {x + y}} \ right) & {\ text {if}} x + y> 0 \\\ pi + \ operatorname {arccot} (\ cot (\ operatorname {arccot} x + \ operatorname {arccot} y)) = \ pi + \ operatorname {arccot} \ left ({\ frac {xy-1} {x + y}} \ right) & { \ text {if}} x + y <0 \\\ end {matrix}} \ right.}

Из этого следует, в частности, для двойных значений функции

2арктан⁡Иксзнак равно{арктан⁡(2Икс1-Икс2)если Икс2<1π+арктан⁡(2Икс1-Икс2)если Икс≥ а также Икс2>1-π+арктан⁡(2Икс1-Икс2)если Икс< а также Икс2>1{\ displaystyle 2 \ arctan x = \ left \ {{\ begin {matrix} \ arctan \ left ({\ frac {2x} {1-x ^ {2}}} \ right) & {\ text {if}} x ^ {2} <1 \\\ pi + \ arctan \ left ({\ frac {2x} {1-x ^ {2}}} \ right) & {\ text {if}} x \ geq 0 {\ текст {и}} x ^ {2}> 1 \\ — \ pi + \ arctan \ left ({\ frac {2x} {1-x ^ {2}}} \ right) & {\ text {if}} x <0 {\ text {and}} x ^ {2}> 1 \\\ end {matrix}} \ right.}

2арккот⁡Иксзнак равно{арккот⁡(Икс2-12Икс)если Икс>π+арккот⁡(Икс2-12Икс)если Икс<{\ displaystyle 2 \ operatorname {arccot} x = \ left \ {{\ begin {matrix} \ operatorname {arccot} \ left ({\ frac {x ^ {2} -1} {2x}} \ right) & { \ text {if}} x> 0 \\\ pi + \ operatorname {arccot} \ left ({\ frac {x ^ {2} -1} {2x}} \ right) & {\ text {if}} x <0 \\\ end {matrix}} \ right.}

Из первого закона может быть достаточно небольшим с
Икс,у{\ displaystyle x, y}

Икс⊕узнак равнозагар⁡(арктан⁡Икс+арктан⁡у)знак равноИкс+у1-Иксу{\ displaystyle x \ oplus y: = \ tan (\ arctan x + \ arctan y) = {\ frac {x + y} {1-xy}}}

вывести в групповой закон . Например, применимо следующее:
⊕{\ displaystyle \ oplus}

12⊕13знак равно12+131-1Шестойзнак равно1,{\ displaystyle {\ frac {1} {2}} \ oplus {\ frac {1} {3}} = {\ frac {{\ frac {1} {2}} + {\ frac {1} {3} }} {1 — {\ frac {1} {6}}}} = 1,}

из чего

арктан⁡12+арктан⁡13знак равноарктан⁡12+131-1Шестойзнак равноарктан⁡1знак равноπ4-й{\ displaystyle \ arctan {\ frac {1} {2}} + \ arctan {\ frac {1} {3}} = \ arctan {\ frac {{\ frac {1} {2}} + {\ frac { 1} {3}}} {1 — {\ frac {1} {6}}}} = \ arctan {1} = {\ frac {\ pi} {4}}}

рассчитано. Кроме того, применяется

1п⊕14-йп3+3пзнак равно4-йп3+4-йп4-йп4-й+3п2-1знак равно4-йп(п2+1)(4-йп2-1)(п2+1)знак равно4-йп4-йп2-1знак равно2⊙12п{\ displaystyle {\ frac {1} {n}} \ oplus {\ frac {1} {4n ^ {3} + 3n}} = {\ frac {4n ^ {3} + 4n} {4n ^ {4} + 3n ^ {2} -1}} = {\ frac {4n (n ^ {2} +1)} {(4n ^ {2} -1) (n ^ {2} +1)}} = {\ гидроразрыв {4n} {4n ^ {2} -1}} = 2 \ odot {\ frac {1} {2n}}}

и соответственно

арктан⁡1пзнак равно2арктан⁡12п-арктан⁡14-йп3+3п.{\ displaystyle \ arctan {\ frac {1} {n}} = 2 \, \ arctan {\ frac {1} {2n}} — \ arctan {\ frac {1} {4n ^ {3} + 3n}} .}

Два уравнения, записанные в виде арккотангенса:

арккот⁡2+арккот⁡3знак равноарккот⁡Шестой-12+3знак равноарккот⁡1знак равноπ4-й{\ displaystyle \ operatorname {arccot} {2} + \ operatorname {arccot} {3} = \ operatorname {arccot} {\ frac {6-1} {2 + 3}} = \ operatorname {arccot} {1} = {\ frac {\ pi} {4}}}

а также

арккот⁡пзнак равно2арккот⁡(2п)-арккот⁡(4-йп3+3п).{\ displaystyle \ operatorname {arccot} {n} = 2 \, \ operatorname {arccot} (2n) — \ operatorname {arccot} (4n ^ {3} + 3n).}

Арккосинус

Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:

Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1<а < 1, то должно получиться две точки, которым соответствуют два противоположных угла:

Получается, что каждому значению числа а соответствует некоторый угол α. А если есть соответствие, то есть и функция:

α = f (a)

В математике ее называют арккосинусом. Записывается она так:

Вертикальная прямая может пересекать единичную окружность в двух разных точках. Им соответствуют разные углы. Принято считать, что арккосинус – это значение того угла, который лежит в первой или второй четверти, то есть ему соответствует точка, лежащая выше оси Ох. Тогда другая точка пересечения будет соответствовать углу (– arccosa):

Выходит, что арккосинус может принимать только значения из отрезка . Дадим определение арккосинуса:

Задание. Вычислите арккосинус числа 1/2.

Решение. Мы помним, что косинус угла π/3 равен 1/2:

Следовательно, arccos 1/2 – это и есть угол π/3:

Ответ: π/3.

Обратим внимание, что если число а равно 1 или (– 1), то его арккосинус равен нулю в первом случае и π во втором:

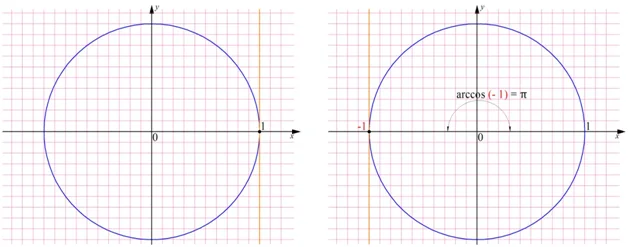
В тех случаях, когда а > 1 либо а <– 1, то соответствующая прямая не пересечет единичную окружность. Это значит, что эти значения не входят в область определения арккосинуса:

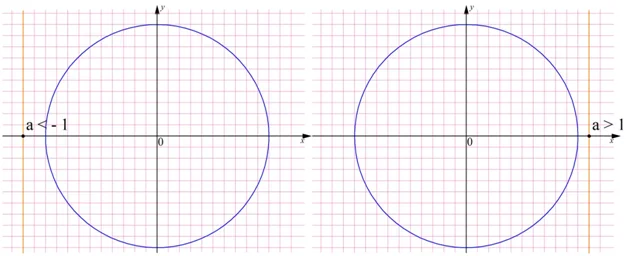
Получается, что область определения арккосинуса – это промежуток .

Для вычисления арккосинусов от отрицательных величин удобно пользоваться формулой

Действительно, если отложить на координатной прямой числа а и (– а), то вертикальные прямые, проходящие через них, пересекут окружность в некоторых точках А и С:

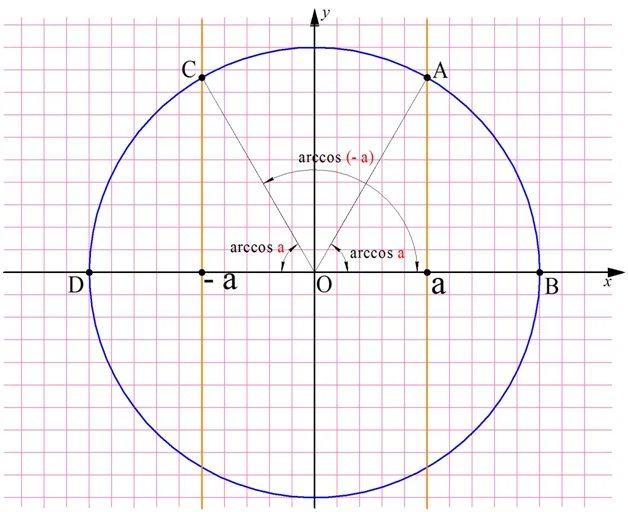
Дополнительно обозначим буквой В точку с координатами (1; 0) и буквой D точку с координатами (– 1; 0). Эти точки располагаются на пересечении оси Ох и единичной окружности. Тогда можно записать, что

ведь эти два угла образуют вместе развернутый угол ВОD, равный π. С другой стороны, из симметрии очевидно, что углы ∠COD и ∠АОВ равны друг другу, значит, ∠COD = ∠АОВ = arccosa. Тогда

Но ∠СОВ – это арккосинус от (– а), поэтому

Задание. Вычислите arccos (– 1/2).

Решение. Используем только что полученную формулу:

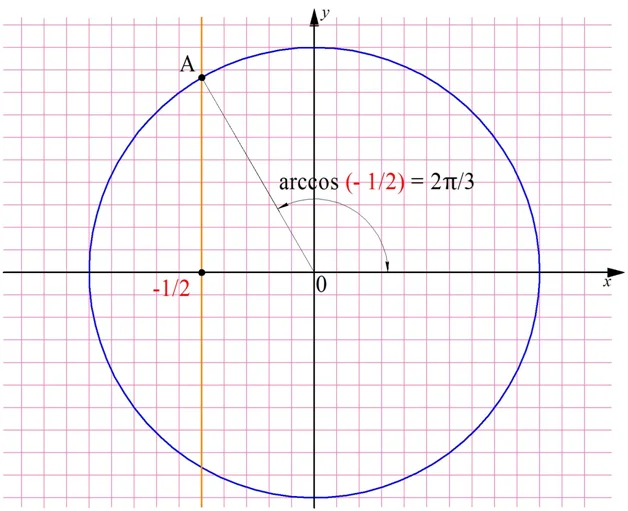
Ответ: 2π/3.

Арккотангенс

Определение 4

Арккотангенс числа $x$ — это множество значений углов, для которых $ctgα = x$.

Свойства функции арккотангенса:

• $D(y)= \ $;
• $E = \ $;
• Данная функция не является ни чётной, ни нечётной;
• Функция $y= arcсtgx$ убывает на всей области определения;

Рисунок 5. График арккотангенса. Автор24 — интернет-биржа студенческих работ

Пример 1

Найдите значение следующих выражений: $arcsin(\frac{1}{2}), arccos(-\frac{\sqrt{2}}{2}), arcctg(\frac{\sqrt{3}}{3}), arccos(-\frac{1}{2})$.

Решение:

$arcsin(\frac{1}{2}) = \frac{π}{6}$

$arccos(\frac{\sqrt{2}}{2}) = \frac{π}{4}$

$arcctg(\frac{\sqrt{3}}{3}) = \frac{π}{4}$

Здесь мы имеем арккосинус отрицательного числа $arccos(-\frac{-1}{2})$, для того чтобы его вычислить, необходимо прибегнуть к следующей формуле:
$arccos(-α) = π – arccos(α)$

$arccos(-\frac{-1}{2}) = π – arccos(\frac{-1}{2}) = π – \frac{π}{3} = \frac{2π}{3}$

Нахождение значения аргумента

Например, найдем все значения аргумента, при которых значение функции

На единичной окружности найдем точки
ординаты которых равны 
Этим точкам соответствуют углы 
и
и таких углов бесконечно много. Однако, если рассмотреть промежуток  то на нем функция 
возрастает и принимает все значения от -1 до 1. Поэтому для любого числа
из промежутка 
существует единственное число  такое что
Так на промежутке
существует единственное значение аргумента, при котором значение функции равно  — это угол равный 
( рис.93)

Определение Арксинуса

Этот угол обозначают 
Так,  поскольку  и 

Вычислите:

Решение:

так как 

Пример №2

Найдите значение выражения:

Решение:

так как

(рис. 95, б).

Заметим, что 
( рис.95)  Так как углы, соответствующие точкам
и
где 
с ординатами 
и
отличаются только знаком, то
для любого числа 
(рис. 96).

Пусть 
тогда 
Так как точки
имеют противоположные ординаты, то 
Поскольку  то по определению арксинуса 
Так как  то для любого числа 
Воспользуемся полученным равенством и найдем значение выражения

Так как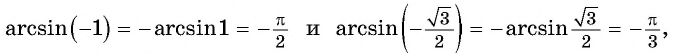 

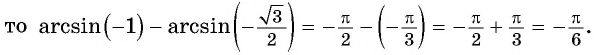
Отметим, что областью определения выражения 
является отрезок  Если 
то выражение не имеет смысла.

Например, выражения  не имеют смысла, так как 
Выражение не имеет смысла, так как 
Из определения арксинуса числа следует, что 
если 

Например,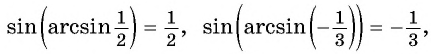 

Рассмотрим промежуток  на котором функция 
возрастает и принимает все значения от до 1. Для любого числа  из промежутка 
существует единственное число  такое, что 

Определение Арккосинуса

Этот угол обозначают 

Например:  поскольку 
и 

Вычислите:

Решение:

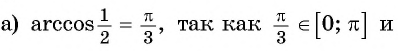
Пример №4

Найдите значение выражения:

Решение:

так как 
( рис. 98.а)

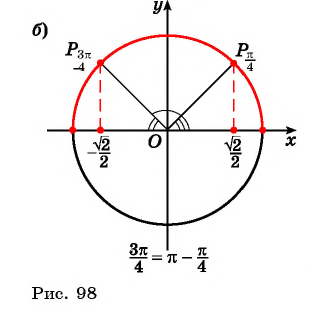
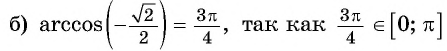
( рис.98.б)

Заметим, что 
( см.98)

Пусть 
Так как точки 
имеют противоположные абсциссы, то 
Поскольку то по определению арккосинуса
Так как для любого числа (рис. 99).

Воспользуемся полученным равенством и найдем значение выражения

Так как 
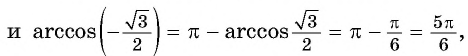
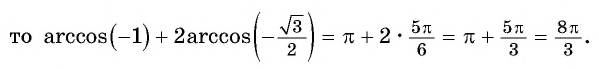
Областью определения выражения  является отрезок 
Если  то выражение не имеет смысла.

Так, выражения
не имеют смысла, поскольку

Выражение 
не имеет смысла, так как 
Из определения арккосинуса числа следует, что
если  и 

Например,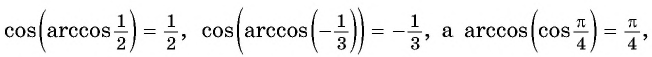 

На промежутке монотонности функции существует единственный угол, тангенс которого равен некоторому данному числу 

Определение Арктангенса

Этот угол обозначают 
Так,  поскольку и 

Вычислите:

Решение:

так как 
и 

и 

Для любого числа 
верно равенство 
(рис. 101).

Пример №6

Найдите значение выражения

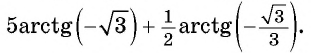
Решение:

Так как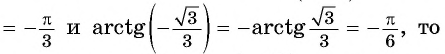 
Из определения арктангенса числа следует, что 
при 

Например,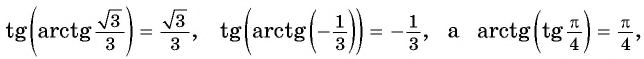 

На промежутке монотонности
функции 
существует единственный угол, котангенс которого равен некоторому данному числу 

Определение Арккотангенса

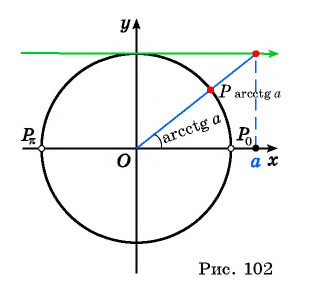
Этот угол обозначают 
Например, поскольку

Вычислите:

Решение:

так как

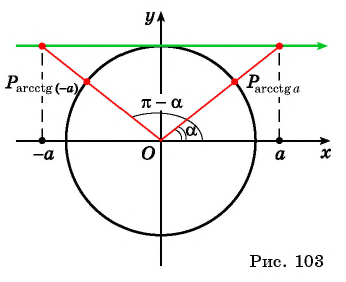
Для любого числа 
верно равенство 
(рис. 103).

Пример №8

Найдите значение выражения 

Решение:

Так как 

Из определения арккотангенса числа следует, что 
если
и 

Например, 

Примеры заданий и их решения

Верно ли, что:

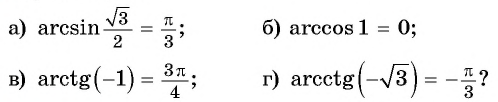
Решение:

• Верно, так как
• верно, так как
• неверно, так как
• неверно, так как

Вычислите:

Решение:

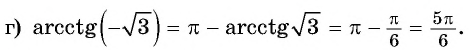
Найдите значение выражения:

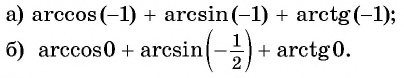
Решение:

Оцените значение выражения 

Решение:

По определению арктангенса числа 

Воспользуемся свойствами числовых неравенств и получим: 

Найдите область определения выражения:

Решение:

• По определению арксинуса числа
  это угол, синус которого равен 
•  По определению арккосинуса числа
  это угол, косинус которого равен 

Найдите значение выражения:

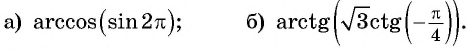
Решение:

Вычислите 

Решение:

Найдите значение выражения 

Решение:

Воспользуемся формулой
при 
Поскольку 
то эту формулу сразу применить нельзя.

Так как 

Разложение в бесконечные ряды[]

arcsin⁡z=z+(12)z33+(1⋅32⋅4)z55+(1⋅3⋅52⋅4⋅6)z77+⋯==∑n=∞((2n)!22n(n!)2)z2n+1(2n+1);|z|≤1.{\displaystyle {\begin{aligned}\arcsin z&{}=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots =\\&{}=\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1.\end{aligned}}}

arccos⁡z=π2−arcsin⁡z==π2−(z+(12)z33+(1⋅32⋅4)z55+(1⋅3⋅52⋅4⋅6)z77+⋯)==π2−∑n=∞((2n)!22n(n!)2)z2n+1(2n+1);|z|≤1.{\displaystyle {\begin{aligned}\arccos z&{}={\frac {\pi }{2}}-\arcsin z=\\&{}={\frac {\pi }{2}}-(z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots )=\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1.\end{aligned}}}

arctgz=z−z33+z55−z77+⋯==∑n=∞(−1)nz2n+12n+1;|z|≤1z≠i,−i.{\displaystyle {\begin{aligned}\operatorname {arctg} \,z&{}=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\\&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i.\end{aligned}}}

arcctgz=π2−arctgz==π2−(z−z33+z55−z77+⋯)==π2−∑n=∞(−1)nz2n+12n+1;|z|≤1z≠i,−i.{\displaystyle {\begin{aligned}\operatorname {arcctg} \,z&{}={\frac {\pi }{2}}-\operatorname {arctg} \,z=\\&{}={\frac {\pi }{2}}-(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots )=\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i.\end{aligned}}}

arcsec⁡z=arccos⁡(z−1)==π2−(z−1+(12)z−33+(1⋅32⋅4)z−55+(1⋅3⋅52⋅4⋅6)z−77+⋯)==π2−∑n=∞((2n)!22n(n!)2)z−(2n+1)(2n+1);|z|≥1.{\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left(z^{-1}\right)=\\&{}={\frac {\pi }{2}}-(z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots )=\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq 1.\end{aligned}}}

arccosecz=arcsin⁡(z−1)==z−1+(12)z−33+(1⋅32⋅4)z−55+(1⋅3⋅52⋅4⋅6)z−77+⋯==∑n=∞((2n)!22n(n!)2)z−(2n+1)2n+1;|z|≥1.{\displaystyle {\begin{aligned}\operatorname {arccosec} \,z&{}=\arcsin \left(z^{-1}\right)=\\&{}=z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots =\\&{}=\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{2n+1}};\qquad \left|z\right|\geq 1.\end{aligned}}}

Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:

arctgx=x1+x2∑n=∞∏k=1n2kx2(2k+1)(1+x2){\displaystyle \operatorname {arctg} \,x={\frac {x}{1+x^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kx^{2}}{(2k+1)(1+x^{2})}}}

(член в сумме при n= 0 принимается равным 1).

Арктангенс, арккотангенс – свойства, графики, формулы

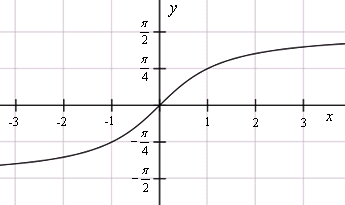
График функции y = arctg x .

График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.

Арккотангенс, arcctg

График функции арккотангенс

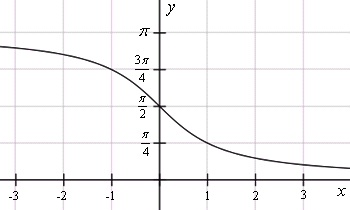
График функции y = arcctg x .

График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.

Четность

Функция арктангенс является нечетной: arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x

Функция арккотангенс не является четной или нечетной: arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .

Свойства – экстремумы, возрастание, убывание

Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.

y = arctg x	y = arcctg x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Множество значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы, минимумы	нет	нет
Нули, y = 0	x = 0	нет
Точки пересечения с осью ординат, x = 0	y = 0	y = π/ 2
–	π

В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.

Функциональные уравнения

Вместо аргументов больше 1 или меньше -1, арктангенс может быть получен из аргументов между -1 и 1:
Икс{\ displaystyle x}узнак равно1Икс{\ displaystyle y = {\ frac {1} {x}}}

арктан⁡Иксзнак равнотак называемый⁡(Икс)⋅π2-арктан⁡1Икс{\ displaystyle \ arctan x = \ operatorname {sgn} (x) \ cdot {\ frac {\ pi} {2}} — \ arctan {\ frac {1} {x}}}.

То же самое и с арккотангенсом:

арккот⁡Иксзнак равно(2-так называемый⁡(Икс))⋅π2-арккот⁡1Икс{\ displaystyle \ operatorname {arccot} x = \ left (2- \ operatorname {sgn} (x) \ right) \ cdot {\ frac {\ pi} {2}} — \ operatorname {arccot} {\ frac {1 } {Икс}}}.

Если вы пришли к аргументу (касательному значению) (например, при первой замене) , вы можете затем использовать уравнение
в случаеу∈,1{\ Displaystyle у \ в }у∈33,1{\ displaystyle \ textstyle y \ in \ left }

арктан⁡узнак равноπ4-й-12⋅арктан⁡(1-у22у),{\ displaystyle \ arctan y = {\ frac {\ pi} {4}} — {\ frac {1} {2}} \ cdot \ arctan \ left ({\ frac {1-y ^ {2}} {2y }} \ Правильно),}

применить так, чтобы аргумент арктангенса остановился в интервале с в любом случае (сейчас , в противном случае ) .
zзнак равно1-у22у{\ displaystyle \ textstyle z = {\ frac {1-y ^ {2}} {2y}}}z{\ displaystyle z}у{\ displaystyle y},33{\ displaystyle \ textstyle \ left }33≈0,577350…{\ displaystyle {\ tfrac {\ sqrt {3}} {3}} \ приблизительно 0 {,} 577350 \ dotso}

Интегралы от обратных тригонометрических функций[]

Неопределённые интегралы

∫arcsin⁡xdx=xarcsin⁡x+1−x2+C,∫arccos⁡xdx=xarccos⁡x−1−x2+C,∫arctgxdx=xarctgx−12ln⁡(1+x2)+C,∫arcctgxdx=xarcctgx+12ln⁡(1+x2)+C,∫arcsec⁡xdx=xarcsec⁡x−ln⁡(x+x2−1)+C,∫arccosecxdx=xarccosecx+ln⁡(x+x2−1)+C.{\displaystyle {\begin{aligned}\int \arcsin x\,dx&{}=x\,\arcsin x+{\sqrt {1-x^{2}}}+C,\\\int \arccos x\,dx&{}=x\,\arccos x-{\sqrt {1-x^{2}}}+C,\\\int \operatorname {arctg} \,x\,dx&{}=x\,\operatorname {arctg} \,x-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcctg} \,x\,dx&{}=x\,\operatorname {arcctg} \,x+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C,\\\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C,\\\int \operatorname {arccosec} \,x\,dx&{}=x\,\operatorname {arccosec} \,x+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C.\end{aligned}}}

Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса

a r c sin , a r c cos , a r c t g и a r c c t g

Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.

Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .

Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.

Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.

Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.

Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.

Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .