5 способов вычисления чисел фибоначчи: реализация и сравнение

Золотое сечение в строении микромиров

Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.

В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.

Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.

Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:

Комментарий Клюга еще раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который ученые классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует четкий замысел и осуществлен разумный проект 16. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру проектами, созданными гениальным архитектором Букминстером Фуллером.

Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.

Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.

В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.

Заблуждения, связанные с числами Фибоначчи

Существует несколько распространенных заблуждений, связанных с числами Фибоначчи. Вот некоторые из них:

Фибоначчи везде и всегда. Часто утверждается, что числа Фибоначчи присутствуют везде в природе, и что все вокруг нас следует этой последовательности. На самом деле, в природе есть много примеров, где можно увидеть числа Фибоначчи, но они не всегда присутствуют повсюду. Иногда формы и структуры в природе обусловлены другими закономерностями и процессами.

• Предсказание рынка с помощью чисел Фибоначчи. Некоторые трейдеры и инвесторы верят, что числа Фибоначчи могут предсказывать точки разворота или продолжения тренда на финансовых рынках.Однако эффективность этих методов остается предметом дебатов. Рыночные движения зависят от множества факторов, и использование только чисел Фибоначчи для прогнозирования может быть недостаточным.
• Золотое сечение везде. Золотое сечение (отношение чисел Фибоначчи) часто приписывается идеалам красоты и гармонии. Однако его применение в искусстве и дизайне не всегда обязательно или универсально применимо.Равновесие и гармония могут быть достигнуты различными способами, и не всегда нужно строго придерживаться золотого сечения.
• Бесконечные свойства последовательности. Иногда говорят, что последовательность Фибоначчи имеет бесконечное количество свойств и применений. Хотя последовательность Фибоначчи действительно обладает рядом интересных свойств, не все из них являются универсальными или общепринятыми. Некоторые свойства могут быть случайными или уникальными для конкретных контекстов и областей.
• Мистические свойства чисел Фибоначчи. Некоторые люди приписывают числам Фибоначчи мистические и магические свойства. Они утверждают, что числа Фибоначчи содержат глубокие секреты Вселенной и являются ключом к различным тайнам. Однако такие утверждения не подтверждаются научными исследованиями и относятся больше к области эзотерики и псевдонауки.

Важно отметить, что числа Фибоначчи, несмотря на свою привлекательность и интересные свойства, не являются универсальным решением или ответом на все вопросы. Их применение и значения могут варьироваться в различных областях и контекстах

Всегда важно подходить к изучению чисел Фибоначчи с научной основой и критическим мышлением, чтобы не заблудиться в море мифов и недостоверной информации.

Заблуждения, связанные с числами Фибоначчи

Благодаря современной поп-культуре с этой числовой последовательностью связано множество популярных мифов:

• Универсальность. Во многих источниках числа Фибоначчи и золотая спираль позиционируются как универсальный закон мироздания, с помощью которого можно описать любой природный процесс или объекты, от расположения лепестков цветка до формы спиральных галактик. Хотя в отношении многих природных явлений это действительно так, принцип не является всеобъемлющим: например, те же рукава спиральных галактик или раковина моллюска наутилуса закручены по логарифмической спирали, которая, хоть и близка по форме к золотой, все же ей не является.
• Идеальность. Распространено мнение, что золотое сечение и спираль Фибоначчи описывают идеальные пропорции. Однако исследования показали, что объекты, построенные по этому принципу (например человеческое тело), при демонстрации обычным людям воспринимаются обычно как диспропорциональные, вытянутые. Отсюда является заблуждением и утверждение, что все великие художники эпохи Возрождения и последующих времен использовали принцип золотой спирали в своих работах. Такие эксперименты действительно случались, но это не было распространенным явлением.
• Практическая применимость. Еще один миф говорит о том, что использование золотого сечения и чисел Фибоначчи в любом сфере деятельности дает положительный результат. Но, например, криптографы знают, что метод Фибоначчи с запозданием не является идеальным способом усилить шифрование — многие генераторы случайных чисел на его основе либо медленно работают, либо имеют недостаточный порог устойчивости к взлому. А использование принципов золотого сечения в архитектуре или промышленном дизайне редко сочетается с оптимизацией производства.

Вместе с тем нельзя отрицать большую роль фибоначчиевых чисел в развитии фундаментальной и прикладной математики, информатики и смежных с ними наук. Разработанные на основе золотой спирали методы и технологии широко применяются в разных областях человеческой жизни, от сугубо научных до прикладных, таких как компьютерная графика, криптография, программирование, обработка данных и т.д.

Выберите IT-профессию, которая вам нравится, а мы поможем научиться:

Другие термины на «Ч»

Чат-бот
Все термины

Тело человека и золотое сечение

Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону Золотой пропорции.

Самая главная книга всех современных архитекторов справочник Э.Нойферта «Строительное проектирование» содержит основные расчеты параметров туловища человека, заключающие в себе золотую пропорцию.

Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы:

M/m=1,618

Первый пример золотого сечения в строении тела человека: Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.

Кроме этого есть и еще несколько основных золотых пропорции нашего тела:

* расстояние от кончиков пальцев до запястья до локтя равно 1:1.618;

* расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618;

* расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618;

* расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618;

* расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618;

* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;

* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618:

Золотое сечение в чертах лица человека как критерий совершенной красоты.

В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.

К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.

На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:

* Высота лица / ширина лица;

* Центральная точка соединения губ до основания носа / длина носа;

* Высота лица / расстояние от кончика подбородка до центральной точки соединения губ;

* Ширина рта / ширина носа;

* Ширина носа / расстояние между ноздрями;

* Расстояние между зрачками / расстояние между бровями.

Где используются числа Фибоначчи

Они нашли широкое применение в различных областях:

• Математика: последовательность служит основой для многих математических задач и теорем.
• Компьютерная наука: они используются в алгоритмах, связанных с оптимизацией и обработкой данных.
• Финансы: применяется в техническом анализе для предсказания поведения рынка и определения уровней поддержки и сопротивления.
• Биология: последовательность Фибоначчи наблюдается в росте и размножении некоторых живых организмов.

Применение этой закономерности в архитектуре является еще одним интересным аспектом этого математического открытия. Здания, созданные на их основе, обладают особым эстетическим очарованием и гармонией. Например, пирамиды Гизы и Парфенон в Афинах были спроектированы с использованием этих пропорций.

В природе этот математический феномен также встречаются повсюду. Расположение ветвей деревьев, структура кристаллов и снежинок, устройство молекул ДНК – все это лишь некоторые из многочисленных примеров присутствия этой последовательности в окружающем мире. Такая универсальность чисел Фибоначчи свидетельствует о глубоких закономерностях, лежащих в основе природы и математики.

Современные исследования продолжают раскрывать новые области их применения. Например, в области компьютерного моделирования и графики эта феноменальная закономерность используются для создания реалистичных изображений и анимации, которые эффективно имитируют реальные сцены и объекты.

В криптографии эта математическая последовательность чисел Фибоначчи также играет важную роль. Она используются в различных алгоритмах шифрования и генерации случайных значений, что обеспечивает повышенную степень защиты данных и информации. Это свидетельствует о том, что числа Фибоначчи остаются актуальными и важными в наше время, также как, например, в русском языке разряды местоимений.

В области физики феномен применяется для изучения квантовых явлений, таких как переплетение и декогеренция. Эти числа также обнаружены в нанотехнологиях, где они определяют определенные характеристики кристаллических структур и молекулярных связей.

В области экономики последовательность также оказывает влияние на фундаментальные принципы и стратегии управления финансовыми ресурсами. В экономической теории и моделировании эти числа используются для анализа финансовых рынков и прогнозирования экономических циклов, что способствует более эффективному и точному управлению рисками и инвестициями.

В биологии это математическое явление имеет существенное значение, особенно в изучении генетики и морфологии различных организмов. Распределение чисел Фибоначчи в структуре хромосом и молекул ДНК указывает на определенные закономерности наследственности и эволюции, что помогает ученым лучше понять процессы развития и адаптации живых систем.

Интересный факт: в музыке числа Фибоначчи и золотое сечение используются для создания гармоничных и пропорциональных музыкальных структур, таких как аккорды, ритмы и мелодии.

Формула Бине

Формула Бине — это формула, которая может использоваться для вычисления n-го члена последовательности Фибоначчи, а это именно то, что мы хотим сделать; эта формула названа в честь открывшего её французского математика Жака Филиппа Мари Бине. Вот она:

Формула Бине для вычисления n-ного числа Fibonacci

Вы можете заметить греческую букву PHI (ϕ), она означает золотое сечение:

Уравнение золотого сечения, phi

Можно написать формулу на Python и сразу же начать работать с ней:

Примечание: для реализации на Python нам нужно вернуть округление вычисляемого числа, потому что при вычислении большого числа Python вернёт результат, в котором может быть более двадцати девяток после запятой.

Всё это хорошо, так как теперь у нас нет никаких циклов и мы можем мгновенно вычислить ответ, верно? Что ж, в этом методе есть небольшая загвоздка. Если мы попытаемся вычислить что-либо выше 1475-го числа, то столкнёмся с ошибкой: OverflowError: (34, result too large). Это связано с тем, как в python реализованы числа с плавающей точкой, они могут иметь конкретное максимальное значение, которое мы превышаем, когда используем этот метод.

Однако исправить ситуацию очень легко. Мы можем использовать встроенный модуль под названием decimal, чтобы создать десятичный объект с гораздо более высокой точностью и подходящим для работы с уравнением размером:

В этой новой функции мы устанавливаем значение точности длиной 10000 цифр, преобразуем наше значение квадратного корня из 5 в десятичное значение объекта и используем его в нашем уравнении. Это позволяет нам легко вычислить 10000-е число в последовательности за поразительные 0,0692986 секунды, а это по сравнению со всеми нашими предыдущими методами огромное улучшение.

Тождества[]

Fn=det(11⋯−111⋱⋮−1⋱⋱⋮⋱⋱⋱1⋯−11){\displaystyle F_{n}=\det {\begin{pmatrix}1&1&0&\cdots &0\\-1&1&1&\ddots &\vdots \\0&-1&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &1\\0&\cdots &0&-1&1\end{pmatrix}}}, а также  Fn+1=det(1i⋯i1i⋱⋮i⋱⋱⋮⋱⋱⋱i⋯i1){\displaystyle \ F_{n+1}=\det {\begin{pmatrix}1&i&0&\cdots &0\\i&1&i&\ddots &\vdots \\0&i&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &i\\0&\cdots &0&i&1\end{pmatrix}}},

где матрицы имеют размер n×n{\displaystyle n\times n}, i{\displaystyle i} — мнимая единица.

Для любого n,

(111)n=(Fn+1FnFnFn−1).{\displaystyle {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n}={\begin{pmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{pmatrix}}.}

Эта формула даёт быстрый алгоритм вычисления чисел Фибоначчи.

(−1)n=Fn+1Fn−1−Fn2{\displaystyle (-1)^{n}=F_{n+1}F_{n-1}-F_{n}^{2}}

Примечания

1. См., например, Т. В. Кропотова, В. Г. Подольский, П. Е. Кашаргин. Введение в высшую математику. — Казанский федеральный университет институт физики.
2. , p. 3.
3. Числа Фибоначчи //  :  / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
4. .
5. , p. 180.
6. Goonatilake, Susantha (1998), , Indiana University Press, с. 126, ISBN 978-0-253-33388-9
7. ↑
8. ↑ Knuth, Donald (2006), , vol. 4. Generating All Trees – History of Combinatorial Generation, Addison–Wesley, с. 50, ISBN 978-0-321-33570-8
9. Knuth, Donald (1968), , vol. 1, Addison Wesley, с. 100, ISBN 978-81-7758-754-8
10. , p. 197.
11. , pp. 404—405.
12. . The University of Utah (13 декабря 2009). Дата обращения: 28 ноября 2018.
13. Knott, Dr. Ron . University of Surrey (25 сентября 2016). Дата обращения: 27 ноября 2018.
14. Knott, Ron . University of Surrey Faculty of Engineering and Physical Sciences.
15. Gardner, Martin (1996), Mathematical Circus, The Mathematical Association of America, с. 153, ISBN 978-0-88385-506-5
16. . artofproblemsolving.com. Дата обращения: 9 мая 2021.
17. Фибоначчи числа // Энциклопедический словарь юного математика / Сост. Савин А. П.. — 2-е изд. — М.: Педагогика, 1989. — С. 312—314. — 352 с. — ISBN 5715502187.
18. ↑ .
19. .
20. .
21. .
22. .
23. .
24. .
25. . planetmath.org. Дата обращения: 30 мая 2021.
26. .
27. Волошинов А. В. Математика и искусство. Москва: Просвещение, 2000. 400 с. ISBN 5-09-008033-X
28. Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. СПБ. Издательство: Питер, 2006. 320 с. ISBN 5-469-01369-3

Рекурсия и числа Фибоначчи в математике

При помощи задачи о кроликах Фибоначчи предварил метод рекуррентных соотношений, как мощный метод решения комбинаторных задач. Один из вариантов по- простому увидеть рекурсию — посмотреть в зеркало, перед которым поставили еще одно зеркало. Повторное отражение зеркал создает видимость тоннеля. Разбор вложенных друг в друга матрешек тоже пример рекурсивного выполнения.

Процесс обращается сам к себе, но с параметром, уменьшенным на 1 от начального. Рекурсия по латыни recurrens обозначает возврат, повторение. Конечная рекурсия служит для упрощения сложной задачи, процесса, вычисления, приводит к ним самим же, но «полегче», а те к более простым, решаемым сразу.

В математике, информатике, программировании без применения рекурсии не обойтись. Рекурсия чисел Фибоначчи — это правило (формула), по которому по нескольким последовательным элементам можно получить любой следующий член заданного числового ряда.

В методах определения функций и числовых рядов применяется математическая рекурсия. Примеры рекурсивных определений натуральных чисел, древовидных структур дискретной математики, функции вычисления факториала числа m, сортировки массива.

1. Один есть натуральное число; целое число, следующее за натуральным, есть натуральное число.
2. Дерево это множество, которое состоит из корня и соединенных с ним поддеревьев, они тоже являются деревьями. Дерево формализуется через самое себя. Рекурсия здесь конечна, т.к. поддерево имеет меньше узлов, чем включающее его дерево.
3. Факториал от m — это произведение всех натуральных чисел от 1 до m.

m!=1*2*3*..(m-1)*m. Требуемый m факториал вычисляется по значению предыдущего (m-1)!.

Числа Фибоначчи в природе

Сам Фибоначчи упоминал эти числа в связи с такой задачей: «Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?». Решением этой задачи и будут числа последовательности, называемой теперь в его честь. Впрочем, описанная Фибоначчи ситуация — больше игра разума, чем реальная природа.

Индийские математики Гопала и Хемачандра упоминали числа этой последовательности в связи с количеством ритмических рисунков, образующихся в результате чередования долгих и кратких слогов в стихах или сильных и слабых долей в музыке. Число таких рисунков, имеющих в целом долей, равно .

Числа Фибоначчи появляются и в работе Кеплера 1611 года, который размышлял о числах, встречающихся в природе (работа «О шестиугольных снежинках»).

Интересен пример растения — тысячелистника, у которого число стеблей (а значит и цветков) всегда есть число Фибоначчи. Причина этого проста: будучи изначально с единственным стеблем, этот стебель затем делится на два, затем от главного стебля ответвляется ещё один, затем первые два стебля снова разветвляются, затем все стебли, кроме двух последних, разветвляются, и так далее. Таким образом, каждый стебель после своего появления «пропускает» одно разветвление, а затем начинает делиться на каждом уровне разветвлений, что и даёт в результате числа Фибоначчи.

Вообще говоря, у многих цветов (например, лилий) число лепестков является тем или иным числом Фибоначчи.

Также в ботанике известно явление »филлотаксиса». В качестве примера можно привести расположение семечек подсолнуха: если посмотреть сверху на их расположение, то можно увидеть одновременно две серии спиралей (как бы наложенных друг на друга): одни закручены по часовой стрелке, другие — против. Оказывается, что число этих спиралей примерно совпадает с двумя последовательными числами Фибоначчи: 34 и 55 или 89 и 144. Аналогичные факты верны и для некоторых других цветов, а также для сосновых шишек, брокколи, ананасов, и т.д.

Для многих растений (по некоторым данным, для 90% из них) верен и такой интересный факт. Рассмотрим какой-нибудь лист, и будем спускаться от него вниз до тех пор, пока не достигнем листа, расположенного на стебле точно так же (т.е. направленного точно в ту же сторону). Попутно будем считать все листья, попадавшиеся нам (т.е. расположенные по высоте между стартовым листом и конечным), но расположенными по-другому. Нумеруя их, мы будем постепенно совершать витки вокруг стебля (поскольку листья расположены на стебле по спирали). В зависимости от того, совершать витки по часовой стрелке или против, будет получаться разное число витков. Но оказывается, что число витков, совершённых нами по часовой стрелке, число витков, совершённых против часовой стрелки, и число встреченных листьев образуют 3 последовательных числа Фибоначчи.

Впрочем, следует отметить, что есть и растения, для которых приведённые выше подсчёты дадут числа из совсем других последовательностей, поэтому нельзя сказать, что явление филлотаксиса является законом, — это скорее занимательная тенденция.

Золотое сечение в природе

Пропорции золотого сечения можно наблюдать во всех природных и научных проявлениях. В представленном списке мы рассмотрим наиболее удивительные случаи.

• Лепестки у цветов. Нередки случаи, когда их количество соответствует числовому ряду «Ф». По мнению Дарвина, все лепестки растений располагаются так, чтобы получать как можно больше солнечного света и остальных необходимых для жизни ресурсов.
• Головки у семян. Во многих случаях семена цветов начинают расти посередине головки семени и появляются снаружи, заполняя собой пространство. В качестве примера можно привести семена подсолнуха.
• Шишки у сосен. Семена, находящиеся в их семенных коробочках, произрастают вверх противоположно друг другу по спирали. Расстояние между ними обычно совпадает с соотношениями чисел из последовательности Фибоначчи.
• Ветки у деревьев. На примере их формирования и расщепления также можно заметить правило золотого ряда. То же самое относится и к развитию корневых систем у растений и водорослей.
• Раковины. Большинство из них демонстрируют нам правило золотого сечения. Например, это можно сказать об улитках и наутилусах.

Золотое сечение в природе

• Спиральные галактики. Млечный Путь содержит в себе несколько рукавов, представленных в виде изогональных спиралей с шагом около 12 градусов. Их форма соответствует форме золотой спирали, при том над каждой такой галактикой можно начертить золотой прямоугольник.
• Ураганы. В большинстве случаев, изнутри они устроены согласно последовательности ряда «фи».
• Пальцы на руках у людей. Все участки пальцев от начала основания и до запястья увеличивается в соотношении по Фибоначчи.
• Тела людей и животных. Расстояние у людей от пупка до пола, а также от темени и до пупка — это яркий пример закона золотого сечения. Помимо человека такую пропорцию можно наблюдать и у других организмов (например, у дельфинов и пчел).
• Молекулы ДНК. Все они содержат соотношение 34 на 21 ангстрем в каждом полном спиральном цикле. А вы уже знаете, что эти цифры — часть ряда Фибоначчи.

Для вас подарок! В свободном доступе до
10.09

Скачайте ТОП-10
нейросетей, которые помогут облегчить вашу работу

Чтобы получить подарок, заполните информацию в открывшемся окне

Перейти

Скачать
файл

Как мы видим, примеров, где можно увидеть пропорции и соотношения по принципу золотого правила, довольно много. Помимо случаев, описанных выше, 1,618 постоянно встречается в точных науках, биологии и других областях жизни. Поэтому свое альтернативное название — божественное сечение, правило полностью оправдывает. Ведь материальный мир словно был создан по этому закону.

Оптимальное решение задачи

Давайте будем представлять два подряд идущих элемента последовательности Фибоначчи как вектор-строку с размерам $$$1$$$ x $$$2$$$, то есть:

Нам нужно научиться умножать нашу вектор-строку на какую-то матрицу $$$A$$$, чтобы мы смогли получить следующую вектор-строку, то есть:

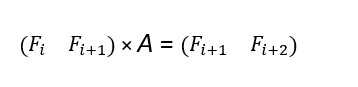
Так как количество строк первой матрицы такое же, как и у итоговой матрицы, то это означает, что мы можем подобрать некоторую матрицу $$$A$$$.

Поскольку мы знаем размеры первого множителя и того, что получилось в результате умножения, то мы сможем узнать размеры матрицы $$$A$$$ — это будет $$$2$$$ x $$$2$$$ (Поскольку количество строк у матрицы $$$A$$$ должно совпадать с количеством столбцов первой матрицы, а количество столбцов итоговой матрицы должно совпадать с количеством столбцов матрицы $$$A$$$). То есть матрица $$$A$$$ имеет вид:

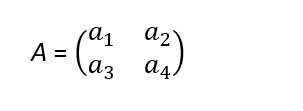
Давайте найдем произведение первой вектор-строки и матрицы $$$A$$$:

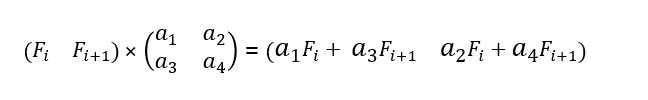
Нам надо, чтобы выполнилось следующее равенство:

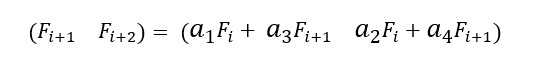
А так как мы знаем, что $$$F_{i + 2} = F_{i + 1} + F_{i}$$$, то $$$a_2 = 1$$$, $$$a_4 = 1$$$. И поскольку очевидно, что $$$F_{i + 1} = F_{i + 1}$$$, то $$$a_1 = 0$$$, $$$a_3 = 1$$$. Получается, что матрица $$$A$$$ будет иметь вид:

Мы нашли такую матрицу $$$A$$$, что умножив на нее матрицу из двух чисел Фибоначчи с индексами $$$i$$$, $$$i + 1$$$, мы получаем новую матрицу из двух чисел Фибоначчи с индексами $$$i + 1$$$, $$$i + 2$$$. Поэтому следующее выражение будет верно:

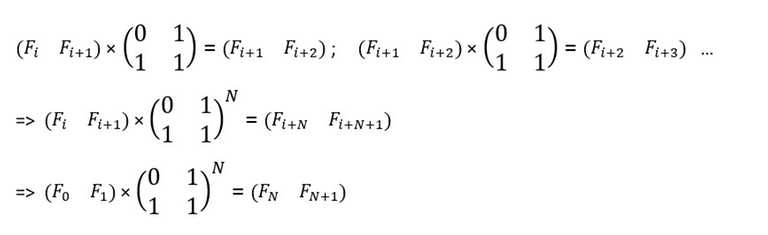
Наше решение будет заключаться в том, что мы вектор-строку с числами Фибоначчи с индексами $$$0$$$ и $$$1$$$ ($$$F_0 = 0$$$, $$$F_1 = 1$$$) будем умножать на матрицу $$$A$$$ в степени $$$n$$$, а затем из итоговой вектор-строки выведем первое число (то есть число, стоящее на пересечении $$$1$$$ — ой строки и $$$1$$$ — ого столбца).

И как многие уже догадались, мы будем возводить матрицу $$$A$$$ в степень $$$n$$$ при помощи быстрого возведения в степень. Для матрицы $$$A$$$ она будет выглядеть так:

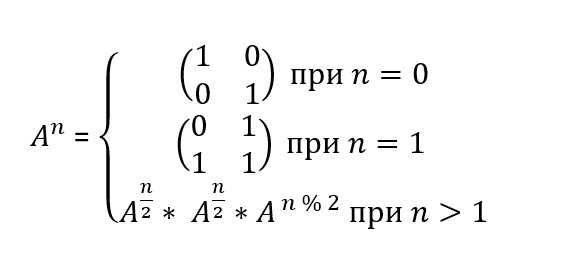
В данном случае, $$$\frac{n}{2}$$$ обозначает деление $$$n$$$ на $$$2$$$ с округлением вниз, а $$$n$$$ % $$$2$$$ — остаток при делении на $$$2$$$. Больше информации про быстрое возведение в степень можно найти в интернете.

Все! Мы научились решать данную задачу, осталось ее реализовать.

Асимптотика по времени данного кода будет составлять $$$O(log_2 n)$$$, поскольку мы вычисляем $$$F_n$$$ — ное число Фибоначчи при помощи быстрого возведения в степень, асимптотика которого как раз составляет $$$O(log_2 n)$$$. И поэтому время выполнения кода будет гораздо быстрее, чем $$$1$$$ секунда.

Последняя цифра числа Фибоначчи

• Формат ввода: Целое число $n$.
• Формат вывода: Последняя цифра $F_n$.
• Ограничения: $0 \le n \le 10^6$.
• Примеры

Пример 3

Ввод	Вывод
91239	6

Предупреждение: будьте аккуратны с целочисленным переполнением. Значение $F_{139}=50,095,301,248,058,391,139,327,916,261$ превосходит диапазон стандартных целочисленных типов, а количество цифр в $F_{91239}$ более $19,000$, но последняя точно 6.

Решение: Взять каждое промежуточное звено по модулю 10

Для решения этой задачи мы вычислим $F_n$ и просто выведем последнюю цифру последовательности:

Обратите внимание, что числа Фибоначчи растут очень быстро. Например, $$
F_{100}=354,224,848,179,261,915,075.
$$. Таким образом, если вы используете типы C++ int32 или int64 для хранения $F$, вы быстро придёте к целочисленному переполнению

Если вы используете числа произвольной точности, например, BigInteger в Java или встроенные целые числа в Python, то вы заметите, что цикл проходит намного медленнее при повышающемся числе итераций

Таким образом, если вы используете типы C++ int32 или int64 для хранения $F$, вы быстро придёте к целочисленному переполнению. Если вы используете числа произвольной точности, например, BigInteger в Java или встроенные целые числа в Python, то вы заметите, что цикл проходит намного медленнее при повышающемся числе итераций.

Остановитесь и подумайте:Последняя цифра в $F_{102}$ — $6$ и последняя цифра в $F_{103}$ — $7$. Какова последняя цифра в $F_{104}$?

Несложно увидеть, что последняя цифра в $F_{104}$ равна $3$, и она полностью определена последними цифрами в $F_{102}$ и $F_{103}$. Это подсказывает нам, как сделать алгоритм практичнее: вместо вычисления $F_n$ и использования последней цифры можно взять каждое промежуточное звено по модулю 10.

Главный посыл этой задачи: когда вам нужно вычислить результат последовательности арифметических операций по модулю $m$, берите результат каждой операции по модулю $m$. Так можно гарантировать, что числа, с которыми вы работаете, будут маленькими (они уместятся в стандартный тип языка программирования, который вы предпочитаете) и что арифметические операции с ними будут выполняться быстро.

Числа Фибоначчи — это что?

Поразителен тот факт, что при делении каждого последующего числа числовой последовательности на предыдущее получается число, стремящееся к 1,618.

Обнаружил эту загадочную последовательность счастливчик математик средневековья Леонардо Пизанский (более известный под именем Фибоначчи). До него Леонардо да Винчи обнаружил в строении тела человека, растений и животных удивительным образом повторяющуюся пропорцию Фи = 1,618. Это число (1,61) ученые еще называют «Числом Бога».

До Леонардо да Винчи эта последовательность чисел была известна в Древней Индии и Древнем Египте. Египетские пирамиды построены с применением пропорции Фи = 1,618. 

Но и это еще не все, оказывается законы природы Земли и Космоса каким-то необъяснимым образом подчиняются строгим математическим законам последовательности чисел Фидоначчи.

Например, и ракушка на Земле, и галактика в Космосе построены с применением чисел Фибоначчи. Абсолютное большинство цветов имеет 5, 8, 13 лепестков. В подсолнухе, на стеблях растений, в закрученных вихрях облаков, в водоворотах и даже в графиках изменения курсов валют на Форексе, всюду работают числа Фибоначчи.

Посмотрите простое и занимательное пояснение, что такое последовательность чисел Фибоначчи и Золотое сечение в этом КОРОТКОМ ВИДЕО (6 минут):

https://youtube.com/watch?v=kayX8XTjL9E

Что такое Золотое сечение или Божественная пропорция?

Итак, что такое Золотое сечение или Золотая или Божественная пропорция? Фибоначчи также обнаружил, что последовательность, которая состоит из квадратов чисел Фибоначчи является еще большей загадкой. Попробуем графически изобразить в виде площади последовательность:

1², 2², 3², 5², 8²…

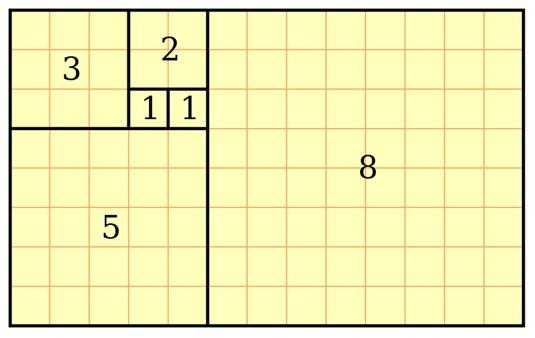Если вписать спираль в графическое изображение последовательности квадратов чисел Фибоначчи, то мы получим Золотое сечение, по правилам которого построено все во вселенной, включая растения, животных, спираль ДНК, человеческое тело, … Список этот можно продолжать до бесконечности.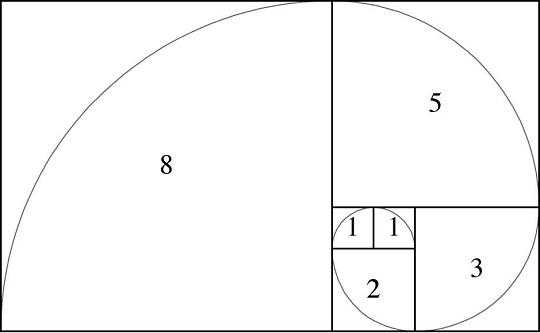

Золотое сечение и Числа Фибоначчи в природе ВИДЕО

Предлагаю посмотреть короткий фильм (7 минут), в котором раскрываются некоторые загадки Золотого сечения. 

При размышлениях о законе чисел Фибоначчи, как о первостепенном законе, который управляет живой и неживой природой, появляется вопрос: Эта идеальная формула для макромира и микромира возникла сама или ее кто-то создал и удачно применил?

Что ВЫ думаете по этому поводу? Давайте вместе подумаем над этой загадкой и быть может мы приблизимся к тайне мироздания.

Очень надеюсь, что статья была полезной для Вас и Вы узнали, что это такое Золотое сечение *и Числа Фибоначчи? До новых встреч на страницах блога, подписывайтесь на блог. Форма подписки — под статьей.

Не могу не поделиться с Вами коротким документальным фильмом — ученые обнаружили загадочную связь между кодом ДНК и числом Бога.