Действия со степенями и корнями

Вынесение множителя из-под корня

Для понимания сути данного преобразования, необходимо сформулировать определение:

Вынесение множителя из-под корня – это замена подкоренного выражения на произведение. Например:

\{B^{n^{*}}} C=B * \sqrt{C}\], где n – нечётное число;

Если n – чётное число, то преобразование выглядит так:

\{B^{n^{*}} C}=\left.B\right|^{*} \sqrt{C}\]

Где B и C – другие числа выражения;

Имея квадратный корень, то есть n=2, вынесение множителя выглядит, как замена выражения \ на равное ему произведение \, проведя такое преобразование, мы освобождаем множитель By из-под корня.

Примеры

Вынесем множитель из-под корня \.

Решение:

В данном случае извлечь квадратный корень можно только из числа двадцать пять, что мы и сделаем.

\

Ответ:\

Преобразуем выражение:

\

Мы вынесли из-под корня выражение с переменным \, а не просто числовой
множитель.

Эти примеры показывают вынесение множителя или целого выражения из-под квадратного корня. Однако подобное
преобразование применимо и к корням в прочих степенях n.

Рассмотрим пример с кубическим корнем:

\{(4 * 2 a)^{3} * 2* a^{2}}=4 * a^{2} * \sqrt{2* a^{2}}\]

Преобразуем выражение с корнем в шестой степени в произведение, которое в перспективе упростим методом
вынесения множителя:

\{\left(\frac{1}{4} *\left(x^{2}+y^{2}\right)\right)^{6} * 6 *\left(x^{2}+y^{2}\right)}\], проводим
преобразование в произведение \{6 *\left(x^{2} *
y^{2}\right)}\].

Выяснив, в чём заключается вынесение множителя из-под корня, перейдем к доказательству равенства полученного путем преобразования произведения исходному выражению.

Презентация на тему: » «Вынесение множителя из- под знака корня. Внесение множителя под знак корня» Куданова Татьяна Владимировна Учитель математики МОУ «СОШ 60» [email protected].» — Транскрипт:

1

«Вынесение множителя из- под знака корня. Внесение множителя под знак корня» Куданова Татьяна Владимировна Учитель математики МОУ «СОШ 60»

2

Цели урока: 1. Выработать алгоритм внесение множителя под знак корня и вынесение множителя из-под знака корня, повторить определение квадратного корня и арифметического квадратного корня. 2. Способствовать развитию вычислительных навыков; умению ставить самооценку, развитию наблюдательности. 3. Побуждать учащихся к учебному сотрудничеству на уроке посредством работы в парах, к самостоятельности и требовательности в достижении успехов.

3

Учащиеся должны знать: алгоритмы внесения множителя под знак корня; алгоритм вынесения множителя из-под знака корня; применение свойств квадратного корня к преобразованию выражений, содержащих квадратный корень.

4

Учащиеся должны уметь: 1 уровень -вносить и выносить множитель из-под знака корня; -преобразовывать простые выражения, содержащие квадратные корни, на основе изученного материала. 2 уровень -пользоваться изученными алгоритмами в стандартной и измененной ситуациях; -применять знания при преобразовании выражений в более сложных ситуациях. 3 уровень -применять полученные знания при выполнении заданий в измененной ситуации.

5

Повторение Дайте определение квадратного корня из числа. Дайте определение арифметического квадратного корня. При каких значениях а, выражение имеет смысл? Сформулируйте правило извлечения корня квадратного из четной степени. Мы закончили изучение свойств арифметического квадратного корня, остаётся применять наши знания и умения при решении примеров и задач.

6

Самостоятельная работа на 3 мин. 1. Найдите: а) ; б) ; в) ; г). 2. Вычислите: а) ; б) ; в) ; г). 3. Сравните ( что больше?): а) и ; б) и ; в) 7 и ; г)6 и 5 ; д) и 7

7

Таблица ответов п\пабвг 1804\ а 36

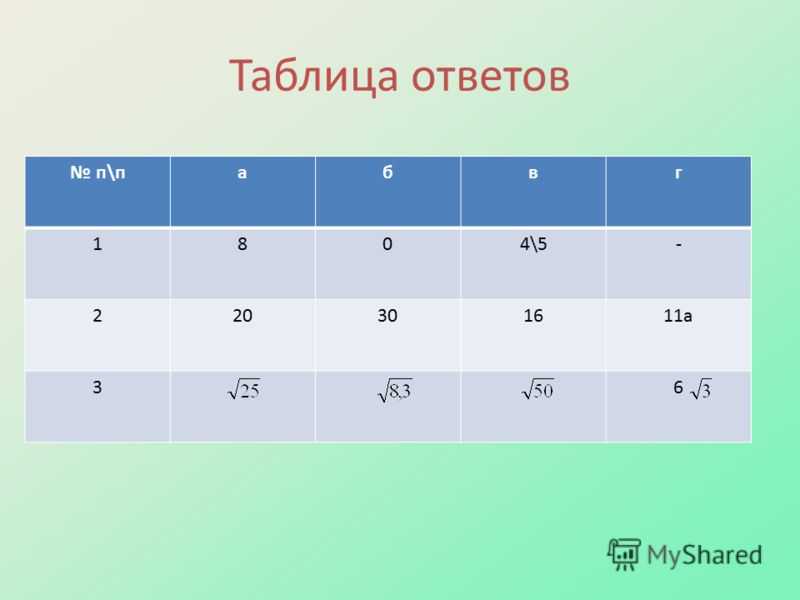
8

Изучение новой темы сравнить объяснение новой темы применение полученных знаний при решении примеров

9

Примеры вынесение множителя из-под знака корня: Внесение под знак корня

10

Закрепление знаний, отработка умений. вынесите множитель из-под знака корня: 407(б, г, е, з) внесите множитель под знак корня: 410(а, в, д), 412(а, в) сравните значения выражений: 414(а, в)

11

Проверка усвоения темы.

12

Итог урока. Задание на дом: Пункт 18, 409(а, в, д, ж); 410(б, г, е); 417(а) 1)Какие способы работы с арифметическим квадратным корнем получили? 2)Как по-другому можно сформулировать тему сегодняшнего урока? 3)На основании каких свойств можно выполнять внесение множителя под знак корня, вынесение множителя из- под знака корня?

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

1. Определить «сотни», между которыми оно стоит.
2. Определить «десятки», между которыми оно стоит.
3. Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

102 = 100

202 = 400

302 = 900

402 = 1600

502 = 2500

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 402и 502.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

12 = 1

22 = 4

32 = 9

42 = 16 ⇒ 6

52 = 25 ⇒ 5

62 = 36 ⇒ 6

72 = 49 ⇒ 9

82 = 64 ⇒ 4

92 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 442 и 462.

Далее вычисляем: 44 * 44 = 1936.

46 * 46 = 2116.

Ответ: √2116 = 46

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

11666 : 4 = 2916

2916 : 4 = 729

729 : 3 = 243

243 : 3 = 81

11664	4
2916	4
729	3
243	3
81	81

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

• Вычислите значение квадратного корня: √36
• Вычислите значение квадратного корня: √64*36
• Вычислите значение квадратного корня:
• Вычислите значение квадратного корня:
• Вычислите значение квадратного корня:
• Вычислите значение выражения: 4√16 — 12
• Вычислите значение выражения: 5√9 — 8
• Вычислите значение выражения: 7√25 — 10
• Вычислите значение квадратного корня:
• Вычислите значение квадратного уравнения:
• Вычислите значение квадратного уравнения:
• Извлеките квадратный корень из числа √7056 удобным вам способом
  Как решаем:

  7056	4
  1764	4
  441	3
  147	3
  49	7
  7	7
  1

• Вычислите значение квадратного корня √0,81
  Ответ: √0,81 = 0,9
• Вычислите значение квадратного корня:

  Как решаем:
  = 0,09

• Вычислите значение выражения: 8√81 — 20
  Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
  Ответ: 8√81 — 20 = 52.
• Вычислите значение выражения: 13√100 — 15
  Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
  Ответ: 13√100 — 15 = 115.
• Вычислите значение выражения: √16 + 5√4
  Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24.
• Вычислите значение выражения: √36 + 2√9
  Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
  Ответ: √36 + 2√9 = 12.
• Вычислите значение выражения: 2√16 — 3√25
  Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
  Ответ: 2√16 — 3√25 = -7.
• Вычислите значение выражения: 3√81 — 5√9
  Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
  Ответ: 3√81 — 5√9 = 12.
• Вынесите множитель из-под знака корень: √60
  Как решаем: √60 = √15 * √4 = 2√15
  Ответ: √60 = 2√15.
• Вынесите множитель из-под знака корень: √160
  Как решаем: √160 = √16 * √10 = 4√10
  Ответ: √160 = 4√10.
• Внесите множитель под знак корня: 6√7
  Как решаем: √62 * 7 = √36 * √7 = √252
  Ответ: 6√7 = √252.
• Внесите множитель под знак корня: 8√2
  Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128.
• Внесите множитель под знак корня: 9√5
  Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
  Ответ: 9√5 = √405.
• Упростите выражение: (5 — √2)2
  Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
  Ответ: (5 — √2)2 = 27 — 10√2.
• Вычислите значение выражения: 3√49 — 3√25
  Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
  Ответ: 3√49 — 3√25 = 6.
• Вычислите значение квадратного корня: √484 * √576
  Как решаем: √484 * √576 = 22 * 24 = 528
  Ответ: √484 * √576 = 528.
• Вычислите значение квадратного корня: √625 * √81
  Как решаем: √625 * √81 = 25 * 9 = 225
  Ответ: √625 * √81 = 225.
• Найдите значение выражения: 3√100 — √144
  Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
  Ответ: 3√100 — √144 = 18.

Обобщение понятия о показателе степени

Постановка задачи: Напомним определение степени с натуральным показателем и ее свойства.

Определение

Основные свойства степени

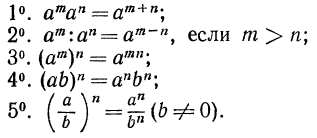
В последующих пунктах речь пойдет об определениях степени с любым рациональным показателем.

Сначала мы определим степень с положительным дробным показателем, далее степень с нулевым показателем и затем степень с отрицательным рациональным показателем. Ясно, что ни на один из этих случаев не переносится данное выше определение, например нельзя определить как произведение числа а самого на себя 3/5 раза. Поэтому каждый раз придется вводить новое определение. При выборе нового определения мы будем руководствоваться требованием, чтобы на новый случай степени распространялись свойства, аналогичные свойствам 1°—5°, перечисленным выше.

Степень с положительным дробным показателем

Пусть Надо определить так, чтобы выполнялось, например, равенство т. е. чтобы при возведении степени в степень показатели перемножались. Но это равенство возможно лишь в случае, когда Возникает вполне естественная мысль: определить Но будет ли такое определение удачным, т. е. будут ли при таком определении выполняться свойства, аналогичные свойствам 1°—5°? Проверим это.

Доказательство. Согласно предложенному определению степени с положительным дробным показателем имеем: Значит, Воспользовавшись свойствами радикалов, приведем радикалы к одному показателю и выполним умножение:

Далее имеем значит,

Доказательство:

Воспользуемся свойствами возведения радикала в степень и извлечения корня из корня:

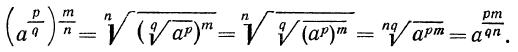
Аналогично можно показать, что будут выполняться свойства:

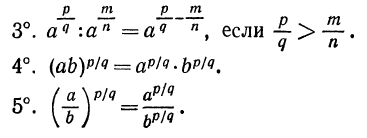
Итак, при предложенном определении степени с положительным дробным показателем основные свойства степени выполнены. Значит, определение удачно и его можно принять.

Определение:

Если

Например, так как так как

На практике при выполнении действий над радикалами довольно часто переходят к дробным показателям.

Примеры:

Выполнить умножение:

Решение:

2.Разложить на множители

Решение:

Первый способ:

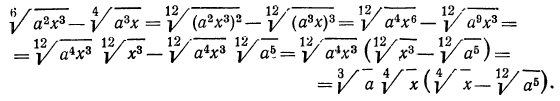
Второй способ:

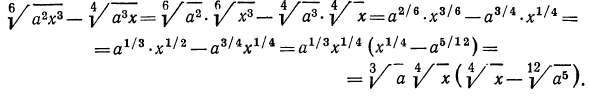
Степень с нулевым показателем

При выборе определения мы также будем руководствоваться требованием, чтобы на случай степени с нулевым показателем распространялись свойства 1°—5° степени с натуральным показателем (впрочем, теперь мы уже вправе говорить о распространении свойств степени с положительным рациональным показателем). В частности, при умножении степеней с одинаковым основанием показатели должны складываться, т. е. должно выполняться равенство

так как (n—натуральное число). Это равенство при возможно лишь в случае, когда Поэтому возникает мысль определить как 1. Нетрудно проверить, что при таком определении выполняются свойства, аналогичные свойствам 1° — 5° степени с натуральным показателем, значит, определение можно принять.

Определение:

Если

Например,

Степень с отрицательным рациональным показателем

Пусть положительное рациональное число. Надо определить так, чтобы, например, выполнялось равенство

Так как то равенство (1) возможно лишь, если определить Нетрудно показать , что при таком определении будут выполняться свойства, аналогичные свойствам 1°—5°.

Покажем, например, что

В самом деле,

Остальные свойства проверяются аналогично.

Определение:

Если

Например,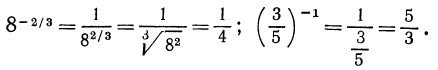

Замечание:

Если r—целое число, то полагают а и в случае, когда а < 0.

Степень с любым рациональным показателем

Мы определили понятие степени с любым рациональным показателем. Эта степень обладает следующими свойствами (мы полагаем а > 0, b > 0, — произвольные рациональные числа):

Заметим, что после введения нулевого и отрицательного показателей мы имеем право в свойстве 2° не делать оговорки, что

Квадратные корни из чисел

Рациональные числа

При рациональных \displaystyle{ a } уравнение \displaystyle{ x^2=a } не всегда разрешимо в рациональных числах. Более того, такое уравнение, даже при положительном \displaystyle{ a }, разрешимо в рациональных числах тогда и только тогда, когда и числитель и знаменатель числа \displaystyle{ a }, представленного в виде несократимой дроби, являются квадратными числами.

Непрерывная дробь для корня из рационального числа всегда является периодической (возможно, с предпериодом), что позволяет, с одной стороны, легко вычислять хорошие рациональные приближения к рациональным числам с помощью линейных рекурсий, а с другой стороны ограничивает точность приближения: \displaystyle{ |\sqrt{r}-p/q|\gt \frac{1}{Cq^2} }, где \displaystyle{ C } зависит от \displaystyle{ r }. Верно и то, что любая периодическая непрерывная дробь является квадратичной иррациональностью.

Примеры разложения корней из натуральных чисел от 2 до 10 в непрерывные дроби:

\displaystyle{ \sqrt{2} }	=
\displaystyle{ \sqrt{3} }	=
\displaystyle{ \sqrt{4} }	=
\displaystyle{ \sqrt{5} }	=
\displaystyle{ \sqrt{6} }	=
\displaystyle{ \sqrt{7} }	=
\displaystyle{ \sqrt{8} }	=
\displaystyle{ \sqrt{9} }	=
\displaystyle{ \sqrt{10} }	=

Действительные (вещественные) числа

Для любого положительного числа \displaystyle{ a } существуют ровно два вещественных корня, которые равны по модулю и противоположны по знаку.

Неотрицательный квадратный корень из неотрицательного числа \displaystyle{ a } называется арифметическим квадратным корнем и обозначается с использованием знака радикала: \displaystyle{ \sqrt a }.

Основные свойства вещественного квадратного корня (все значения под знаком корня считаются положительными):

• \displaystyle{ \sqrt{a^2} = |a|: }
• \displaystyle{ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} } (корень из произведения равен произведению корней из сомножителей);
• \displaystyle{ \sqrt{\frac {a} {b}} = \frac{\sqrt{a}} {\sqrt{b}}\quad (b\ne 0); }

К комплексным числам, учитывая двузначность корня, все эти свойства неприменимы (см. ниже пример ошибки).

Комплексные числа

Квадратных корней из любого ненулевого комплексного числа всегда ровно два, они противоположны по знаку. Для корней в комплексной области понятие арифметического корня не вводится, знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней. В последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Распространённая ошибка:

\displaystyle{ -1=(\sqrt{-1})^2 = \sqrt{(-1)^2}=\sqrt{1}=1 } (что, конечно, неверно)

Ошибка возникла из-за того, что комплексный квадратный корень является двузначной функцией, и его нельзя использовать в арифметических действиях.

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если

\displaystyle{ a=|a|e^{i\phi} },

то (см. Формула Муавра)

\displaystyle{ \sqrt{a}=\sqrt{|a|} \cdot e^{i(\phi+2\pi k)/2} },

где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом, в итоге получаются два различных результата.

Существует и чисто алгебраическое представление для корня из \displaystyle{ a+bi }; оба значения корня имеют вид \displaystyle{ \pm(c+di) } где:

\displaystyle{ c = \sqrt{\frac{a + \sqrt{a^2 + b^2}}{2}} }

\displaystyle{ d = \sgn (b) \sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}} }

Здесь sgn — функция «знак». Формула легко проверяется возведением \displaystyle{ c+di } в квадрат.

Пример: для квадратного корня из \displaystyle{ 3+4i } формулы дают два значения: \displaystyle{ 2+i;\; -2-i. }

Квадратный корень как элементарная функция

График функции \displaystyle{ y=\sqrt x }

Квадратный корень является элементарной функцией и частным случаем степенной функции \displaystyle{ x^\alpha } с \displaystyle{ \alpha=1/2 }. Арифметический квадратный корень является гладким при \displaystyle{ x\gt 0, } в нуле же он непрерывен справа, но не дифференцируем.

Производная функции квадратного корня вычисляется по формуле:

\displaystyle{ \frac{d(\sqrt{x})}{dx} = \frac{1}{2\sqrt{x}} }

Как функция комплексного переменного корень — двузначная функция, два листа которой соединяются в нуле (см. подробнее Комплексный анализ).

Извлечение корней

решать примеры с квадратными корнями намного проще, если вы помните как можно больше квадратов чисел. Для этого воспользуйтесь таблицей – сохраните ее себе и используйте для решения задач.

Таблица квадратов

100	121	144	169	196	225	256	289	324	361
400	441	484	529	576	625	676	729	784	841
900	961	1024	1089	1156	1225	1296	1369	1444	1521
1600	1681	1764 г	1849 г	1936 г	2025	2116	2209	2304	2401
2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Вот несколько примеров извлечения корня, чтобы научиться пользоваться таблицей:

1. Извлеките квадратный корень:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Влево — 1, вверх — 7.

Отвечать: .

2. Извлеките квадратный корень:

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Отвечать: .

3. Извлеките квадратный корень:

Ищем в таблице число 7396.

Влево — 8, вверх — 6.

Отвечать: .

4. Извлекаем рут:

Ищем в таблице число 9025.

Влево — 9, вверх — 5.

Отвечать: .

5. Вытащить корень

Ищем в таблице число 1600.

Влево — 4, вверх — 0.

Отвечать: .

извлечение корня называется нахождением его значения.

Задачи на вынесение множителя из подкоренного выражения

Задачи 1-2

Условие: необходимо вынести множитель из четырех подкоренных выражений: \{8} * \sqrt{4},
\sqrt{5 \frac{1}{16}}, \sqrt{(-0,4)^{7} * 11}, \sqrt{\sqrt{7}}\]

Решение:

Учитывая вид подкоренных выражений и показатели корней, запишем следующее:

• Применим свойства корней: \{a b}=\sqrt{a} * \sqrt{b}\]
  \{8} *
  \sqrt{4}=\sqrt{8 * 4}=\sqrt{32}=2\]
• Учитывая четный показатель корня и его свойства, преобразуем выражение: \{5
  \frac{1}{16}}=\sqrt{\frac{81}{16}}=\frac{\sqrt{81}}{\sqrt{16}}=\frac{3}{2}\]
• Учитывая нечётный показатель, используем соответствующее правило преобразования: \{(-0,4)^{7} *
  11}=-0,4 * \sqrt{11}\]
  Или другой вариант расчета:\{(-0,4)^{7} * 11}=\sqrt{(-1)^{7} *(0,4)^{7} *
  11}=\sqrt{(0,4)^{7} * 11}=-0,4 * \sqrt{11}\]
• Учитывая свойство \{ \sqrt{a}}=\sqrt{a}\] (в том случае, если k больше 0) \{\sqrt{7}}=\sqrt{7}\]

Условие: необходимо преобразовать выражение \.

Решение:

Выведем из-под корня три множителя:

\

Ответ: \

Далее подробнее разберемся с подкоренным выражением, требующим предварительного преобразования.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

ДРУГОЕ

Как извлечь корень кубический

Перед вами стоит задача извлечения кубического корня из числа. Значок корня с цифрой три рядом может по-началу запутать…

Число, которое находится под знаком корня, часто мешает решению уравнения, с ним неудобно работать. Даже если оно…

Как преобразовать в многочлен выражение

Многочленом называется сумма одночленов, то есть произведений цифр и переменных. Работать с ним удобнее, так как чаще…

Как возвести корень в квадрат

Возведение числа в степень — это сокращенная форма записи операции многократного умножения, в котором все множители…

Как вычитать квадратный корень

В операциях с математическими выражениями, содержащими квадратные корни, от знаков радикала желательно избавиться.…

Как внести множитель под корень

Корнем из числа x называется такое число, которое при возведении в степень корня будет равно x. Множителем называется…

Внести множитель под знак корня или вынести его оттуда – это достаточно распространенная операция, которую часто…

Результатом выполнения операции извлечения корня должно быть число, которое при возведении его в степень, равную…

Как упростить квадратный корень

Если подкоренное выражение содержит набор математических действий с переменными, то иногда в результате его упрощения…

Как перемножить корни

Арифметические действия с корнями различной степени могут значительно упростить расчеты в физике и технике и сделать их…

Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, ?x =…

Как возвести в корень число

Операция возведения числа в степень означает нахождение результата умножения его на себя такое количество раз, которое…

Корнем n степени из числа называют такое число, которое при возведении в эту степень даст то число, из которого…

Как найти корень степени из числа

Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни…

Как вносить под знак корня

При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные…

Как внести число под корень

Корнем называют значок, обозначающий математическую операцию нахождения такого числа, возведение которого в указанную…

Как извлечь корень в степени из числа

Математическая операция извлечения корня означает нахождение такого значения, при возведении которого в заданную…

Как вынести из-под знака корня

Знаком корня в математических науках называется условное обозначение для корней. Число, находящееся под знаком корня,…

Как вынести число из корня

В большинстве случаев бывает проще посчитать на калькуляторе подкоренное выражение. Но если необходимо решить задачу в…

Арифметическим корнем n-й степени из действительного числа a называют такое неотрицательное число x, n-я степень…

Как сравнивать корни

Корнем n-ой степени из действительного числа a называется такое число b, для которого выполняется равенство b^n = a.…

Алгебра

18. Вынесение множителя за знак корня. Внесение множителя под знак корня

Сравним значения выражений и 6. Чтобы решить эту задачу, преобразуем . Представим число 50 в виде произведения 25 • 2 и применим теорему о корне из произведения. Получим

Так как 5 < 6, то < 6.

При решении задачи мы заменили произведением чисел 5 и . Такое преобразование называют вынесением множителя за знак корня.

Значения выражений и 6 можно сравнить иначе, представив произведение 6 в виде арифметического квадратного корня. Для этого число 6 заменим и выполним умножение корней.

Получим

Так как 50 < 72, то < . Значит,

< 6.

При решении задачи вторым способом мы заменили 6 выражением . Такое преобразование называют внесением множителя под знак корня.

Пример 1. Вынесем множитель за знак корня в выражении .

Решение: Выражение имеет смысл лишь при а ≥ 0, так как если а < 0, то а7 < 0.

Представим подкоренное выражение а7 в виде произведения а6 • а, в котором множитель а6 является степенью с чётным показателем.

Тогда

Пример 2. Внесём множитель под знак корня в выражении — 4.

Решение: Отрицательный множитель — 4 нельзя представить в виде арифметического квадратного корня, и поэтому множитель — 4 нельзя внести под знак корня. Однако выражение — 4 можно преобразовать, внеся под знак корня положительный множитель 4:

Пример 3. Внесём множитель под знак корня в выражении a.

Решение: Множитель а может быть любым числом (положительным, нулём или отрицательным). Поэтому рассмотрим два случая:

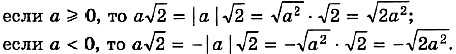
Упражнения

407. Вынесите множитель за знак корня:

408. Вынесите множитель за знак корня и упростите полученное выражение:

409. Вынесите множитель за знак корня:

410. Внесите множитель под знак корня:

411. Какое из выражений не имеет смысла?

412. Представьте выражение в виде арифметического квадратного корня или выражения, ему противоположного:

413. Замените выражение арифметическим квадратным корнем или выражением, ему противоположным:

414. Сравните значения выражений:

415. Сравните значения выражений:

416. Расположите в порядке возрастания числа:

417. (Задача-исследование.) Проверьте, верны ли равенства

     Выясните, каким должно быть соотношение между числами а и b, чтобы было верно равенство , где а ∈ N и b ∈ N.

     1) Возведите в квадрат обе части равенства.
     2) Установите, каким должно быть соотношение между числами а и b.
     3) Проиллюстрируйте правильность вашего вывода на примерах.

418. (Для работы в парах.) Площадь треугольника S см2 со сторонами а см, b см и с см можно вычислить по формуле Герона:

     где р — полупериметр треугольника.

     Пользуясь калькулятором, найдите площадь треугольника, стороны которого равны:

     а) 12 см, 16 см, 24 см;
     б) 18 см, 22 см, 26 см.

     1) Распределите, кто выполняет задание а), а кто — задание б), и выполните вычисления.
     2) Проверьте друг у друга правильность вычислений.
     3) Обсудите, как изменится площадь треугольника, если каждую из его сторон увеличить в 2 раза. Выскажите предположение и выполните необходимые преобразования.

419. В школьной мастерской учащиеся за три дня переплели 144 книги. Сколько книг было переплетено в каждый из трёх дней, если известно, что во второй день учащиеся переплели на 12 книг больше, чем в первый, а в третий — числа книг, переплетённых в первый и во второй дни вместе?

420. Решите уравнение:

Основной принцип

Распределительный закон умножения позволяет умножить число на сумму (или сумму на число). Например, чтобы найти значение выражения 3 × (4 + 5) можно умножить число 3 на каждое слагаемое в скобках и сложить полученные результаты:

3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15

Число 3 и выражение в скобках можно поменять местами (это следует из переместительного закона умножения). Тогда каждое слагаемое, которое в скобках, будет умножено на число 3

 (4 + 5) × 3 = 4 × 3 + 5 × 3= 12 + 15

Пока не будем вычислять конструкцию 3 × 4 + 3 × 5 и складывать полученные результаты 12 и 15. Оставим выражение в виде 3(4 + 5) = 3 × 4 + 3 × 5. Ниже оно нам потребуется именно в таком виде, чтобы понять суть вынесения общего множителя за скобки.

Распределительный закон умножения иногда называют внесением множителя во внутрь скобок. В выражении 3 × (4 + 5) множитель 3 был за скобками. Умножив его на каждое слагаемое в скобках, мы по сути внесли его во внутрь скобок. Для наглядности можно так и записать, хоть и не принято так записывать:

3 (4 + 5) = (3 × 4 + 3 × 5)

Поскольку в выражении 3 × (4 + 5) число 3 умножается на каждое слагаемое в скобках, это число является общим множителем для слагаемых 4 и 5

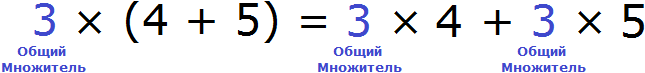
Как говорилось ранее, умножив этот общий множитель на каждое слагаемое в скобках, мы вносим его во внутрь скобок. Но возможен и обратный процесс — общий множитель можно обратно вынести за скобки. В данном случае в выражении 3 × 4 + 3 × 5 общий множитель виден как на ладони — это множитель 3. Его и нужно вынести за скобки. Для этого сначала записывается сам множитель 3

3

и рядом в скобках записывается выражение 3 × 4 + 3 × 5 но уже без общего множителя 3, поскольку он вынесен за скобки

3(4 + 5)

В результате вынесения общего множителя за скобки получается выражение 3(4 + 5). Это выражение тождественно равно предыдущему выражению 3 × 4 + 3 × 5

3(4 + 5) = 3 × 4 + 3 × 5

Если вычислить обе части полученного равенства, то получим тождество:

3(4 + 5) = 3 × 4 + 3 × 5

27 = 27

Формулы корней. Свойства квадратных корней.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555. Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»). В предыдущем уроке мы разобрались, что такое квадратный корень

Пришла пора разобраться, какие существуют формулы для корней
, каковы свойства корней
, и что со всем этим можно делать

В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней
, каковы свойства корней
, и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями
— это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…

Начнём с самой простой. Вот она:

Квадратные корни? | Wyzant Спросите эксперта

Показатели математической алгебры упрощают квадратный корень Индекс квадратных корней

Кортни Дж.

Я не могу понять это, буду признателен за любую помощь! Спасибо!

1.

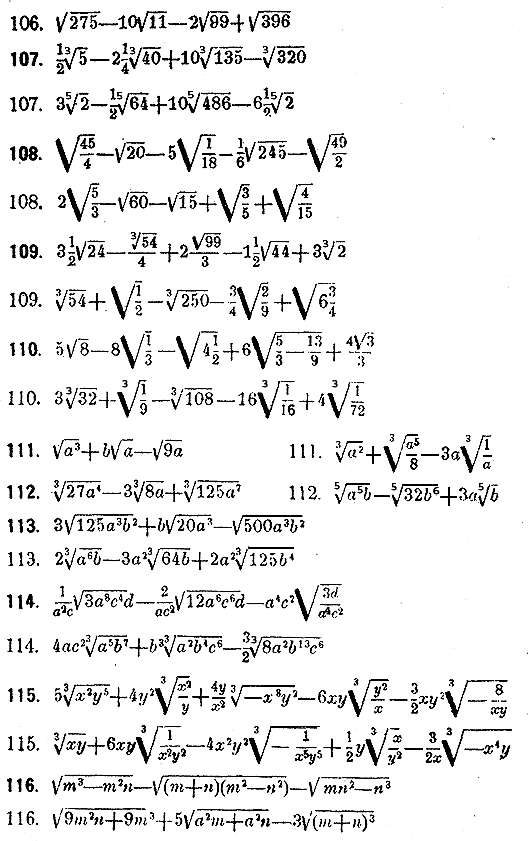
2.   (6√2+8√3)(√2+9√3)

3.   (√6+x) 2

4.   ( 3 √4-6)( 3 √2+6)

5.   (√x-3+5) 2

6.   7y√20y+9√20y 3

Подписаться
І
2

Подробнее

Отчет

1 ответ эксперта

Киша К.
ответил 12.04.13

Репетитор

4.7
(22)

Учиться УДОБНО И ЛЕГКО!!!

Смотрите таких репетиторов

Смотрите таких репетиторов

Привет, Кортни,

Я не собираюсь давать вам ответы на все эти проблемы, потому что это ваша домашняя работа, а не моя :), но я помогу вам научиться решать такие проблемы, поэтому я проиллюстрирую их # 2.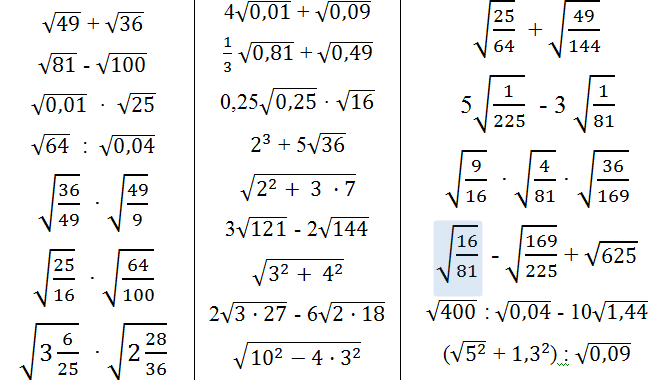

Эта задача одновременно и на умножение квадратных корней, и на сложение… так что давайте сначала обсудим правила.

1. Вы можете складывать или вычитать квадратные корни, только если число под корнем ( √() ) одинаково, например.

√(2) + √(2) = 2√(2).

Это означает, что квадратный корень из 2 плюс квадратный корень из 2 равен 2-кратному квадратному корню из 2… или 2 копиям квадратного корня из 2, как 2x равно x + x .

Вычитание будет таким же образом…

2√(2) — √(2) = √(2)

Нельзя складывать непохожие вещи… например. тот же # не находится под радикалом, поэтому…

√(2) + 9√(3) = √(2) + 9√(3)    ==> Это должно оставаться как — потому что √(2)  и √(3) не одно и то же, это яблоки и апельсины.

РАЗНЫЕ

2. При умножении и делении квадратных корней правила немного меняются…

==> Вы можете умножать только числа, находящиеся под радикалом ( √() ), например.

√(2) * √(3) = √(6)

… но проще это понять: √(2) * √(2) = √(4), что равно 2…но мы знаем это.

3. Деление работает так же, как умножение, за исключением того, что вы можете получить дробь, которая должна остаться.

  √(4) ÷ √(2) на самом деле √(4/2) = √(2) … помните, что √(4) можно записать как √(2)*√(2).. .это облегчает отмену

…но что, если это был √(2) ÷ √(4) ?

Тогда ответ был бы

√(2)

   2

Даже если бы было хуже.

√(8) ÷ √(6)

Но используйте те же принципы, и вы получите…

2√(2)

√(6)

Помните, что 4*2 = 8, а √(4) равно 2, поэтому мы можем убрать это из радикала.

Если мы факторизуем √(6), мы получим √(2) * √(3)… ну, как мы это делали до того, как мы смогли сделать отмену

2       *  √(2)   = 2     * √(2)  = 2  

√(3) * √(2)   = √(3) * √(2)   = √(3)

Этот ответ правильный, но мы обычно не любим квадратные корни или корни любого вида в знаменателе… так что мы умножаем на то же самое, что в знаменателе, чтобы мы могли получить ответ, который выглядит следующим образом:

   2  * √(3)  = 2 √(3)

√(3) * √(3) =    3

Возвращаясь к задаче… ), концепции из FOIL, или просто помните, что каждый член должен быть умножен на другие члены, основанные на свойстве дистрибутива .

Основные свойства корней

Для любого натурального \( n\), целого \( k\) и любых неотрицательных чисел \( a\) и \( b\) выполнены равенства:

\( \sqrt{ab}=\sqrt{a}\cdot \sqrt{b};\)

\( \sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\text{ }\left( b\ne 0 \right);\)

\( \sqrt{\sqrt{a}}=\sqrt{a}\text{ }\left( k>0 \right);\)

\( \sqrt{{{a}^{k}}}=\sqrt{a}\text{ }\left( k>0 \right);\)

при нечетных \( n\): \( \sqrt{{{a}^{k}}}={{\left( \sqrt{a} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ }то\text{ }a\ne 0 \right)\)

при четных \( k\) и \( n\): \( \sqrt{{{a}^{k}}}={{\left( \sqrt{\left| a \right|} \right)}^{k}}\text{ }\left( \text{если }k\le 0,\text{ то }a\ne 0 \right)\)

Понятие внесения множителя под знак корня

Начнем с определения этого преобразования.

Определение 1

Внесение множителя под знак корня представляет собой преобразование произведения B·Cn, где B и C являются числами или выражениями, а n – натуральным числом, в тождественно равное выражение Bn·Cn или -Bn·Cn.

Первое знакомство с этим видом преобразования, как правило, происходит сразу после изучения понятия квадратного корня и его свойств в рамках школьного курса алгебры. При этом определение берется только для n, равного 2, то есть для выражений с квадратным корнем. Позже, когда начинают изучаться корни n-ной степени, разбираются и случаи с более сложными выражениями.

Учитывая все сказанное выше, легко понять, почему данное преобразование называется именно так: в его результате множитель B перемещается под знак корня. Также очевидно, что изменить таким образом можно не любые выражения, а только конкретные произведения некоторых чисел (выражений) и корней, под знаками которых также расположено некоторое число или выражение. В качестве примера можно привести 5·3, -0,7·x+2·y3, x-2·1-x4 и  т.д.

В результате мы должны прийти к выражению вполне определенного вида. Так, указанные выше примеры после преобразования будут выглядеть так: 52·3, -0,73·x+2·y3, -x-24·1-x4. Возможно и дальнейшее упрощение этих выражений, если такая необходимость есть.

После того, как мы определились, что из себя представляет внесение множителя под знак корня, можно перейти к теоретическим обоснованиям преобразования. В следующем пункте мы объясним, когда -Bn·Cn следует заменять на Bn·Cn, а когда Bn·Cn на -Bn·Cn.

Внесение под корень буквы

Чтобы внести букву под знак корня, поступаем так же, как и с числами (в т.ч. с отрицательными) – возводим эту букву в соответствующую степень, после чего добавляем в подкоренное выражение.

Пример 6

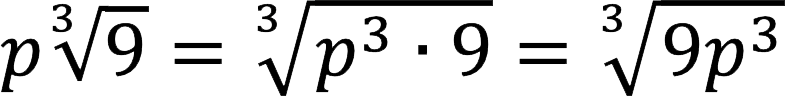
Это справедливо при p > 0, если же p – отрицательное число, то перед знаком корня необходимо добавить знак “минус”.

Пример 7 Рассмотрим более сложный случай: (3 + √8) · √5.

Решение:

1. Сперва внесем выражение в скобках под знак корня.

2. Теперь согласно формуле сокращенного умножения возведем выражение (3 + √8) в квадрат.

Примечание: первый и второй шаг можно поменять местами.

3. Остается только выполнить умножение под корнем с раскрытием скобок.

Действия с корнями

Умножение корней

Как умножать корни? На этот вопрос помогает ответить самое простое и базовое свойство:

\( \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}\)

Начнем с простенького:

\( \sqrt{5}\cdot \sqrt{2}=\sqrt{10}\)\( \sqrt{2}\cdot \sqrt{3}=\sqrt{6}\)Корни из получившихся чисел ровно не извлекаются? Не беда – вот вам такие примеры:

\( \sqrt{2}\cdot \sqrt{8}=\sqrt{16}=4\)\( \sqrt{12,5}\cdot \sqrt{2}=\sqrt{25}=5\)А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:

\( \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{10}=\sqrt{100}=10\)С этим вроде все ясно. Едем дальше. А если перед нами такое выражение:

\( 3\sqrt{5}\)Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из \( 9\)!

\( 3\sqrt{5}=\sqrt{9}\cdot \sqrt{5}=\sqrt{45}\).

Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:

\( 3\sqrt{10}-\sqrt{45}\cdot \sqrt{2}=\sqrt{90}-\sqrt{90}=0\).

Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно!