11 класс. алгебра. степени и корни. степенные функции. корни n-ой степени, их свойства. функция y=ⁿ√x, ее свойства и график. - свойства корня n-ой степени. примеры решения типовых задач.

2. Теорема о корне из произведения, доказательство, примеры

Корень n-й степени (n=2, 3, 4…) из произведения двух неотрицательных чисел равен произведению корней n-й степени из этих чисел.

Дано:

Доказать:

Доказательство:

Обозначим исходные выражения через х, у и z:

Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:

Теорема доказана.

Рассмотрим несколько примеров на применение доказанной теоремы.

Пример 1 – вычислить:

Теорема удобна тем, что не нужно выполнять трудоемкое умножение, а иногда, наоборот, раскладывать большие числа на множители.

Пример 2 – вычислить:

Теорема 1 допускает обобщение, например, для произведения трех сомножителей.

Обобщение:

Дано: ,

Доказать:

Доказательство:

Согласно условию , если рассматривать ab как один множитель, а с как второй, можем применить к выражению теорему 1:

Теперь можем применить теорему 1 к корню из ab:

Обобщение доказано.

Пример 3 – вычислить:

Пример 4 – вычислить:

Арифметический квадратный корень

Вспомним, что такое арифметический квадратный корень.

Уравнение имеет два решения: и .

Это числа, квадрат которых равен .

А как решить уравнение ?

Если мы нарисуем график функции , то увидим, что и у этого уравнения есть два решения, одно из которых положительно, а другое отрицательно.

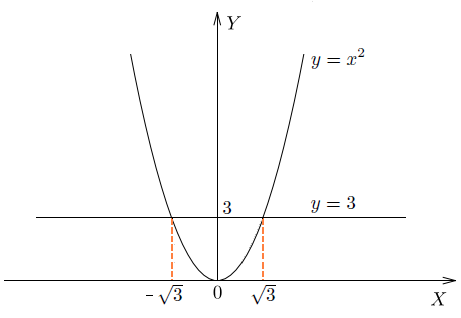
Но эти решения не являются целыми числами. Более того, они не являются рациональными. Для того чтобы записать эти решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

Запомните это определение.

Арифметический квадратный корень обозначается .

Приведем несколько примеров.

Еще раз повторим определение: Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a

Это значит, что (это наши первые два примера). Очевидно,

А с третьим примером интереснее: поскольку по определению.

1) В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при

2) Выражение всегда неотрицательно, т. е. Например,

Свойства арифметического квадратного корня:

Запомним: выражения и не равны друг другу.Легко проверить.

, верно? Как вы думаете, чему в общем случае равен

На этот вопрос мы ответим немного позже. А сейчас решим несколько задач из вариантов Профильного ЕГЭ по математике.

1. Найдите значение выражения

Обратите внимание: не равен

2. Найдите значение выражения

Применили формулу разности квадратов:

Применили формулу квадрата суммы.

4. Найдите значение выражения при

Иногда — например, при решении неравенств — надо сравнить два выражения, содержащих знак корня.

5. Что больше: или ?

Никаких приближенных вычислений!

Напомним еще раз, что , так что «убирать» корни мы не можем.

График функции

Построим график функции Возьмем несколько значений аргумента x, причем таких, что квадратный корень из них является целым числом.

1	4	9	16	25
1	2	3	4	5

Область определения функции:

Область значений функции:

Вот как выглядит график функции

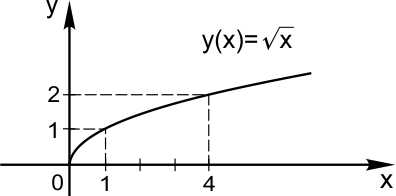
Нарисуем в одной системе координат графики функций и при

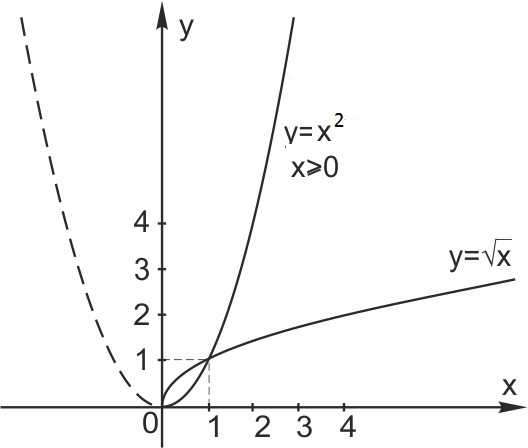
Что же мы видим? При графики функций и симметричны относительно прямой

То, что для функции является областью определения, для функции — область значений (при неотрицательных x).

Такие функции называют взаимно-обратными.

Корень из квадрата:

Если вы внимательно читаете эту статью, то помните, что один вопрос остался без ответа. Чему равен ?

Здесь a — некоторое число или выражение. По определению арифметического квадратного корня, — это такое неотрицательное число, квадрат которого равен Оно равно a при и равно -a при Узнаете определение модуля? Запомним:

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Сравните два выражения: √50 и 9√5

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Это значит, что 6√5 > √18. Сравните два выражения: 7√12 и √20

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Основные свойства и ограничения

У корней много странных свойств и ограничений — об этом будет отдельный урок. Поэтому сейчас мы рассмотрим лишь самую важную «фишку», которая относится лишь к корням с чётным показателем. Запишем это свойство в виде формулы:

Другими словами, если возвести число в чётную степень, а затем из этого извлечь корень той же степени, мы получим не исходное число, а его модуль
. Это простая теорема, которая легко доказывается (достаточно отдельно рассмотреть неотрицательные $x$, а затем отдельно — отрицательные). О ней постоянно талдычат учителя, её дают в каждом школьном учебнике. Но как только дело доходит до решения иррациональных уравнений (т.е. уравнений, содержащих знак радикала), ученики дружно забывают эту формулу.

Чтобы детально разобраться в вопросе, давайте на минуту забудем все формулы и попробуем посчитать два числа напролом:

Это очень простые примеры. Первый пример решит большинство людишек, а вот на втором многие залипают. Чтобы без проблем решить любую подобную хрень, всегда учитывайте порядок действий:

Сначала число возводится в четвёртую степень. Ну, это как бы несложно. Получится новое число, которое даже в таблице умножения можно найти;
И вот уже из этого нового числа необходимо извлечь корень четвёртой степени. Т.е. никакого «сокращения» корней и степеней не происходит — это последовательные действия.

Раберёмся с первым выражением: $\sqrt{{{3}^{4}}}$. Очевидно, что сначала надо посчитать выражение, стоящее под корнем:

Затем извлекаем корень четвёртой степени из числа 81:

Теперь сделаем то же самое со вторым выражением. Сначала возводим число −3 в четвёртую степени, для чего потребуется умножить его само на себя 4 раза:

Получили положительное число, поскольку общее количество минусов в произведении — 4 штуки, и они все взаимно уничтожится (ведь минус на минус даёт плюс). Дальше вновь извлекаем корень:

В принципе, эту строчку можно было не писать, поскольку и ежу понятно, что ответ получится один и тот же. Т.е. чётный корень из той же чётной степени «сжигает» минусы, и в этом смысле результат неотличим от обычного модуля:

Эти вычисления хорошо согласуются с определением корня чётной степени: результат всегда неотрицателен, да и под знаком радикала тоже всегда стоит неотрицательное число. В противном случае корень не определён.

Замечание по поводу порядка действий

Запись $\sqrt{{{a}^{2}}}$ означает, что мы сначала возводим число $a$ в квадрат, а затем извлекаем из полученного значения квадратный корень. Следовательно, мы можем быть уверены, что под знаком корня всегда сидит неотрицательное число, поскольку ${{a}^{2}}\ge 0$ в любом случае;
А вот запись ${{\left(\sqrt{a} \right)}^{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.

Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.

Впрочем, все эти проблемы актуальны лишь для чётных показателей.

Вынесение минуса из-под знака корня

Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:

Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:

Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.

И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!

Доказательство второго свойства

Все последние четыре свойства доказываются аналогично, поэтому ограничимся доказательством только второго: n√(a*b)= n√a*n√b.

Используя определение арифметического корня докажем что n√(a*b)= n√a*n√b.

Для этого докажем два факта, что n√a*n√b. Больше либо равен нулю, и что (n√a*n√b.)^n = ab.

1. n√a*n√b больше либо равно нулю, так как и а и b больше либо равны нулю.
2. (n√a*n√b)^n = a*b, так как (n√a*n√b)^n = (n√a)^n *(n√b)^n = a*b.

Что и требовалось доказать. Значит свойство верно. Эти свойства очень часто придется использовать при упрощении выражений содержащих арифметические корни.

8. Обзор свойств корня n-й степени, примеры

Сделаем обзор свойств корня n-й степени из неотрицательного числа.

, при (теорема 1);

, при (теорема 2);

, при (теорема 3);

, при (теорема 4).

Из теоремы 4 есть важное следствие:

Следует избегать типичных ошибок, обратим на них внимание:

, например .

Перейдем к решению примеров.

Пример 5 – вычислить:

Пример 6:

Пример 7:

Итак, на данном уроке мы вспомнили ранее изученные и рассмотрели новые свойства корня n-й степени из неотрицательного числа, научились возводить его в степень и извлекать корень.

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/11-klass/stepeni-i-korni-stepennye-funktsii/svoystva-kornya-n-oy-stepeni

http://interneturok.ru/ru/school/algebra/11-klass/stepeni-i-korni-stepennye-funktsii/svoystva-kornya-n-oy-stepeni-prodolzhenie

https://www.youtube.com/watch?v=7HIVp5vBbYI

Корни n-ой степени

Аналогично кубическому корню можно ввести понятие и корня произвольной n-ой степени.

Для обозначения корня n-ой степени используется знак радикала, перед которым стоит число n. Приведем пример. Мы знаем, что 25 = 32. Это значит, что корень 5-ой степени из 32 равен 2:

Мы помним, что все вида у = хn схожи друг с другом и при этом могут быть разбиты на два класса, в зависимости от четности или нечетности показателя степени n. Если n– четное число (2, 4, 6…), то график будет похож на параболу у = х2, просто он будет чуть сильнее «прижат» к оси Ох вблизи точки О (0;0), но вместе с тем он будет и быстрее возрастать:

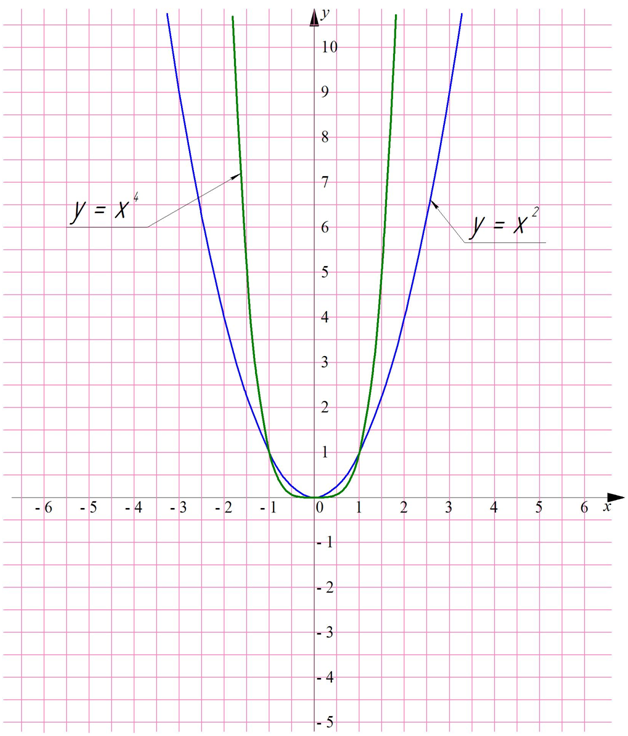
Если же показателем n является нечетное число, то график у = хn будет схож с графиком у = х3:

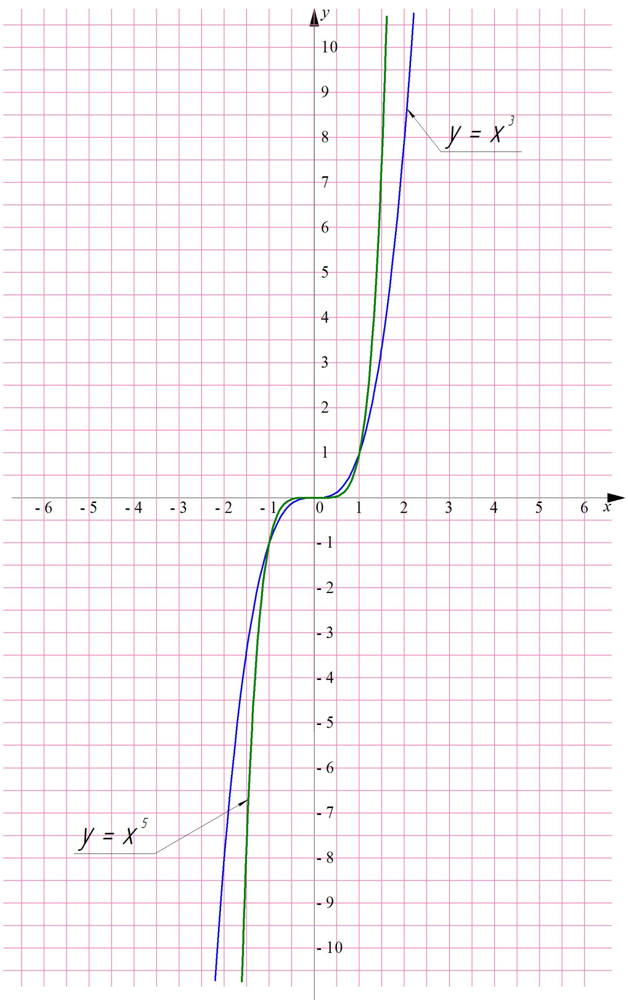
Мы видим, что при нечетном показателе получается строго монотонная (возрастающая) функция. Следовательно, она обратима. Функция, обратная функции у = хn, и будет корнем степени n.

Если n нечетно, то корень можно извлечь и из отрицательного числа. Так, известно, что (– 3)7 = – 2187. Это значит, что корень седьмой степени из (– 2187) равен (– 3):

Очевидно, что корень получится отрицательным, если под ним стоит отрицательное число. Если же подкоренное выражение положительно, то и сам корень положителен. Более того, можно заметить, что корень из отрицательного числа равен корню из противоположенного ему положительного числа, взятого со знаком минус:

В общем случае графики всех корней нечетных степеней будут похожи на график кубического корня:

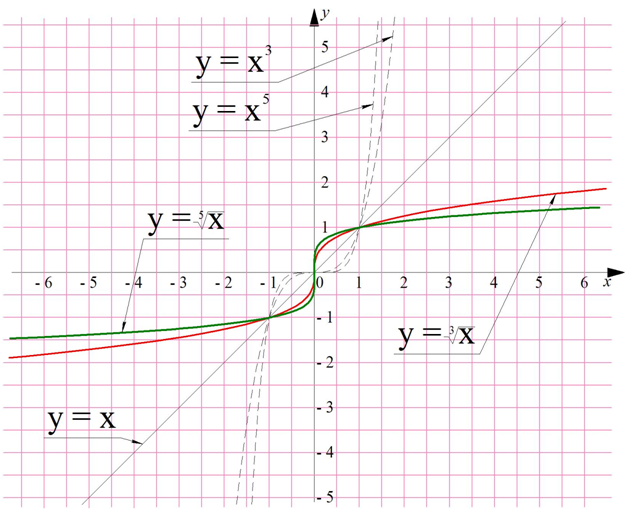
Несколько сложнее дело обстоит в том случае, если показатель n является четным. Мы уже выяснили, что у = х2 – это необратимая функция. Аналогично и любая другая степенная функция у = хn необратима. Однако у = х2 обратима, если наложить дополнительное ограничение: х ≥ 0. Аналогично, при использовании такого же ограничения, обратимой будет и любая функция у = хn, где n – четное число. График такой функции будет похож на квадратный корень:

При четном значении n корень n-ой степени нельзя извлечь из отрицательного числа. Действительно, попробуем возвести в четную степень положительное число:

54 = 5•5•5•5 = 625

Получили другое положительное число. Теперь попробуем возвести в четную степень отрицательное число:

(– 5)4 = (– 5)•(– 5)•(– 5)•(– 5) = 625

Результат снова положительный! Минусы у отрицательных чисел «сократились» друг с другом, и получилось положительное произведение. Но раз при возведении в четную степень всегда получается неотрицательное число, значит, и под четным корнем должно также стоять неотрицательное число. Поэтому подкоренное выражение не может быть отрицательным.

Почему нужны два определения?

Внимательный читатель уже наверняка заметил, что все квадратные корни, приведённые в примерах, извлекаются из положительных чисел. Ну, в крайнем случае из нуля. А вот кубические корни невозмутимо извлекаются абсолютно из любого числа — хоть положительного, хоть отрицательного.

Почему так происходит? Взгляните на график функции $y={{x}^{2}}$:

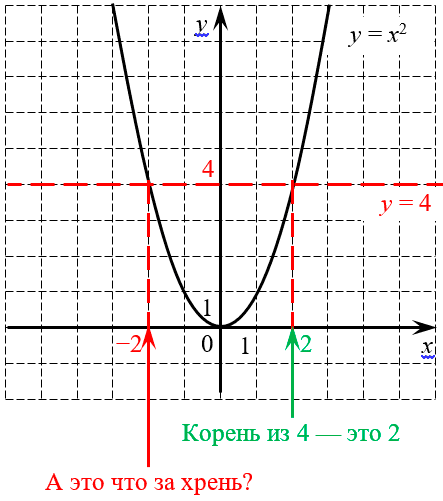График квадратичной функции даёт два корня: положительный и отрицательный

Попробуем с помощью этого графика посчитать $\sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку

С первым числом всё понятно — оно положительное, поэтому оно и есть корень:

Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)

В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.

Подобная проблема возникает у всех корней с чётным показателем:

Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
Из отрицательных чисел корень с чётным $n$ вообще не извлекается.

Именно поэтому в определении корня чётной степени $n$ специально оговаривается, что ответ должен быть неотрицательным числом. Так мы избавляемся от неоднозначности.

Зато для нечётных $n$ такой проблемы нет. Чтобы убедиться в этом, давайте взглянем на график функции $y={{x}^{3}}$:

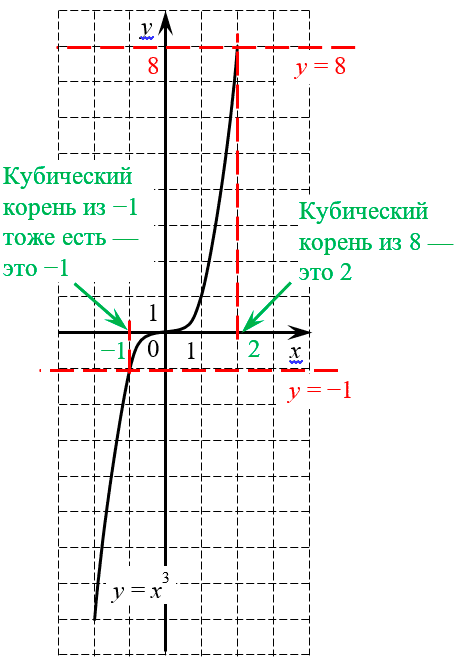Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа

Из этого графика можно сделать два вывода:

Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).

Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.

Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.

Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.

А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:

Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.

Прямая на плоскости

Общее уравнение прямой: Ax+By+C=0.
Уравнение прямой с угловым коэффициентом: y=kx+b (k – угловой коэффициент).
Острый угол между прямыми y=k₁x+b₁ и y=k₂x+b₂ определяется по формуле:

k₁=k₂ — условие параллельности прямых y=k₁x+b₁ и y=k₂x+b_2.
Условие перпендикулярности этих же прямых:

Уравнение прямой, имеющей угловой коэффициент k, и проходящей

через точку М(х₁; у₁), имеет вид: у-у₁=k (х-х₁).

Уравнение прямой, проходящей через две данные точки (х1; у1) и (х2; у2) имеет вид:

Длина отрезка М1М2 с концами в точках М1(х1; у1) и М2(х2; у2):

Координаты точки М(хо; уо) – середины отрезка М1М2

Координаты точки С(х; у), делящей в заданном отношении λ отрезок М1М2 между точками М1(х1; у1) и М2(х2; у2):

Расстояние от точки М(хо; уо) до прямой ax+by+c=0:

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Определить «сотни», между которыми оно стоит.
Определить «десятки», между которыми оно стоит.
Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

102 = 100

202 = 400

302 = 900

402 = 1600

502 = 2500

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 402и 502.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

12 = 1

22 = 4

32 = 9

42 = 16 ⇒ 6

52 = 25 ⇒ 5

62 = 36 ⇒ 6

72 = 49 ⇒ 9

82 = 64 ⇒ 4

92 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 442 и 462.

Далее вычисляем: 44 * 44 = 1936.

46 * 46 = 2116.

Ответ: √2116 = 46

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

11666 : 4 = 2916

2916 : 4 = 729

729 : 3 = 243

243 : 3 = 81

11664	4
2916	4
729	3
243	3
81	81

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

Вычислите значение квадратного корня: √36
Вычислите значение квадратного корня: √64*36
Вычислите значение квадратного корня:
Вычислите значение квадратного корня:
Вычислите значение квадратного корня:
Вычислите значение выражения: 4√16 — 12
Вычислите значение выражения: 5√9 — 8
Вычислите значение выражения: 7√25 — 10
Вычислите значение квадратного корня:
Вычислите значение квадратного уравнения:
Вычислите значение квадратного уравнения:
Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем:

7056 4

1764 4

441 3

147 3

49 7

7 7

1
Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9
Вычислите значение квадратного корня:
Как решаем:
= 0,09
Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52.
Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115.
Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24.
Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12.
Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7.
Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12.
Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15.
Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10.
Внесите множитель под знак корня: 6√7
Как решаем: √62 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252.
Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128.
Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405.
Упростите выражение: (5 — √2)2
Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2)2 = 27 — 10√2.
Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6.
Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528.
Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225.
Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.

Кубический корень

Ранее мы изучили понятие квадратного корня. Напомним, что извлечение квадратного корня – это операция, обратная возведению в квадрат. Другими словами, функция

является обратной для у = х2.

Встает вопрос – а можно ли придумать функцию, обратную возведению в куб? Конечно же да, ведь мы убедились в том, что функция у = х3 обратима. Называют же функцию, обратную у = х3, кубическим корнем.

Можно дать и другое определение, не использующее понятие функции:

Например, мы знаем, что число 5 в кубе равно 125:

53 = 125

Это значит, что кубический корень из 125 равен 5.

Для обозначения кубического корня используют тот же знак радикала, что и для квадратного корня. Чтобы их отличать друг от друга, в случае с кубическим корнем перед знаком радикала ставят тройку:

Заметим важное отличие кубического и квадратного корня. Мы привыкли, что под знаком радикала не должно стоять отрицательное число

Но кубический корень из отрицательного числа извлечь можно. Например, мы знаем, что (– 6)3 = – 216. Отсюда следует, что

График кубического корня можно получить, просто построив функцию, обратную у = х3:

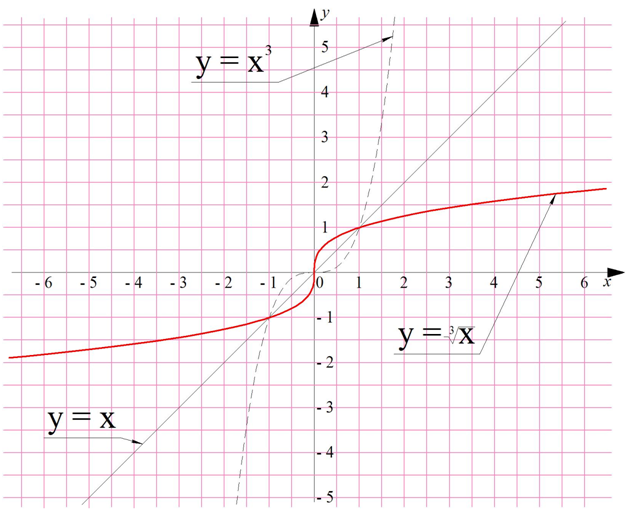
9 класс

№ урока	Тема
1	Повторение материала 8 класса 11 минут 54секунд
2	Повторение материала 8 класса. Решение систем уравнений 13 минут 57секунд
3	Квадратичная функция.y = ax2 12 минут 11секунд
4	Квадратичная функция y = ax2 + bx + c 14 минут 13секунд
5	Графиком квадратичной функции y = ax2 + bx + c. 14 минут 10секунд
6	Область определения функции 14 минут 11секунд
7	Промежутки возрастания и убывания функции 13 минут 51секунд
8	Чётность и нечётность функции 9 минут 51секунд
9	Неравенства и уравнения содержащие степень 14 минут 43секунд
10	Решение задач 12 минут 56секунд
11	Решение задач 11 минут 36секунд
12	Решение систем уравнений второго порядка. 14 минут 21секунд
13	Решение простейших систем, содержащих вторую степень 11 минут 37секунд
14	Решение простейших систем, содержащих вторую степень. 11 минут 37секунд
15	Различные способы решения систем уравнений. 11 минут 11секунд
16	Решение задач (1). 13 минут 5секунд
17	Решение задач.Закрепление (1). 11 минут 36секунд
18	Решение неравенств и систем неравенств второй степени с одной переменной. 9 минут 35секунд
19	Решение примеров. 17 минут 35секунд
20	Решение практических задач. 19 минут 35секунд
21	Решение квадратных неравенств методом интервалов 17 минут 5секунд
22	Решение примеров 15 минут 11секунд
23	Доказательство простых неравенств 14 минут 4секунд
24	Решение примеров 12 минут 17секунд
25	Решение примеров 11 минут 49секунд
26	Решение практических задач. 8 минут 11секунд
27	Решение практических задач. 9 минут 24секунд
28	Радианная мера угла 10 минут 32секунд
29	Поворот точки вокруг начала координат 14 минут 42секунд
30	Определение синуса. Косинуса. Тангенса и Котангенса угла 14 минут 6секунд
31	Решение примеров 13 минут 15секунд
32	Решение примеров 12 минут 38секунд
33	Зависимость между синусом, косинусом и тангенсом одного и того же аргумента 9 минут 39секунд
34	Решение примеров 12 минут 13секунд
35	Тригонометрические тождества 15 минут 18секунд
36	Радианная мера угла 10 минут 36секунд
37	Синус, косинус, тангенс и котангенс углов а И -а 12 минут 54секунд
38	Формулы сложения 11 минут 22секунд
39	Решение примеров 16 минут 16секунд
40	Синус и косинус двойного угла 16 минут 24секунд
41	Формулы приведения 10 минут 12секунд
42	Сумма и разность синусов. Сумма и разность косинусов 17 минут 20секунд
43	Синус, косинус, тангенс и котангенс углов а и -а 12 минут 44секунд
44	Числовые последовательности 17 минут 0секунд
45	Арифметические прогрессия 11 минут 4секунд
46	Сумма n первых членов арифметической прогрессии 11 минут 53секунд
47	Геометрическая прогрессия 10 минут 45секунд
48	Бесконечно убывающая геометрическая прогрессия 19 минут 29секунд
49	Решение задач 19 минут 29секунд
50	Бесконечно убывающая геометрическая прогрессия 10 минут 17секунд
51	Решение задач 9 минут 35секунд
52	Практические и мепредметные задачи (2 часть) 8 минут 26секунд
53	Решение задач (1 часть) 10 минут 1секунд
54	Решение задач (2 часть) 10 минут 1секунд
55	События 16 минут 3секунд
56	Решение задач 6 минут 30секунд
57	Вероятность события 9 минут 9секунд
58	Решение задач 8 минут 56секунд
59	Относительная частота случайного события 11 минут 40секунд
60	Случайные величины (1) 8 минут 5секунд
61	Случайные величины (2 часть) 8 минут 5секунд
62	Числовые характеристики случайных величин 10 минут 39секунд
63	Решение задач 9 минут 4секунд
64	Повторение 9 минут 58секунд

8 класс

№ урока	Тема
1	Повтор. Материала 7кл 12 минут 3секунд
2	Повторение 7 класса 11 минут 59секунд
3	Алгебраические выражения 13 минут 28секунд
4	Решение задач. Алгебраические выражения 20 минут 26секунд
5	Сокращение алгебраических дробей 12 минут 9секунд
6	Приведение алгебраических дробей к общему знаменателю 11 минут 31секунд
7	Сложение и вычитание алгебраических дробей 13 минут 39секунд
8	Решение задач на сложение и вычитание алгебраических дробей 14 минут 3секунд
9	Умножение и деление алгебраических дробей 16 минут 8секунд
10	Решение практических задач 18 минут 2секунд
11	Обратная пропорциональность 16 минут 55секунд
12	Обратная пропорциональность(2) 13 минут 7секунд
13	Арифметический корень натуральной степени 10 минут 44секунд
14	Упрощение алгебраических выражений, содержащих степень 15 минут 54секунд
15	Упрощение алгебраических выражений, содержащих степень с рациональным показателем 15 минут 39секунд
16	Практические и межпредметные задачи 12 минут 44секунд
17	Числовые неравенства 11 минут 6секунд
18	Свойства числовых неравенств 15 минут 48секунд
19	Возведение в степень неравенств 20 минут 26секунд
20	Решение линейных неравенств 14 минут 12секунд
21	Решение линейных неравенств с одной переменной 13 минут 38секунд
22	Решение систем неравенств 19 минут 10секунд
23	Системы неравенств. Числовые промежутки 12 минут 14секунд
24	Решение систем неравенств (2) 13 минут 33секунд
25	Решение задач, на вычисление погрешностей 12 минут 18секунд
27	Модуль числа уравнения и неравенства, содержащие модуль. 37 минут 18секунд
28	Решение примеров 11 минут 24секунд
29	Приближенное вычисление. Приближенные значения величин. Погрешность приближения 11 минут 16секунд
30	Оценка погрешности 13 минут 13секунд
31	Округление чисел 13 минут 8секунд
32	Относительная погрешность 11 минут 25секунд
33	Решение примеров 12 минут 2секунд
34	Квадратное уравнение и его корни 11 минут 19секунд
35	Решение примеров 10 минут 16секунд
36	Неполные квадратные уравнения и их решения 9 минут 35секунд
37	Решение примеров 9 минут 35секунд
38	Формулы нахождения корней квадратного уравнения. Дискриминант 12 минут 46секунд
39	Теорема Виета. Разложение квадратного трехчлена на линейные множители 9 минут 33секунд
40	Решение примеров 20 минут 7секунд
41	Биквадратные уравнения. Уравнения, сводящиеся к квадратным 13 минут 20секунд
42	Решение примеров 15 минут 15секунд
43	Решение задач с помощью квадратных уравнений 17 минут 30секунд
44	Практические и межпредметные задачи 13 минут 20секунд
45	Практические и межпредметные задачи 11 минут 17секунд
46	Решение задач 12 минут 9секунд
47	Средняя величина. Мода. Медиана 11 минут 39секунд
48	Решение задач (1-часть) 13 минут 21секунд
49	Решение задач (2 часть) 10 минут 35секунд
50	Решение комбинаторных задач методом перебора 7 минут 45секунд
51	Решение задач 9 минут 47секунд
52	Основной закон комбинаторики и его применение при решении задач 10 минут 46секунд
53	Решение задач 9 минут 47секунд
54	Практические и межпредметные задачи 10 минут 42секунд
55	Упражнение для повторения курса «Алгебры» 8-класса 15 минут 43секунд
56	Решение задач (1 часть) 9 минут 29секунд
57	Решение задач (часть 2) 7 минут 41секунд
58	Решение задач (часть 3) 7 минут 41секунд

7056	4
1764	4
441	3
147	3
49	7
7	7
1