Основные сведения о рациональных выражениях в алгебре

Натуральные числа $\mathbb{N}$

Множество натуральных чисел часто обозначается как
$\mathbb{N}=\lbrace 1,2,3,4… \rbrace $, и часто его дополняют нулем, обозначая $\mathbb{N}_0$.

В $\mathbb{N}$ определены операции сложения (+) и умножения ($\cdot$) со следующими свойствами для любых $a,b,c\in \mathbb{N}$:

1. $a+b\in \mathbb{N}$, $a\cdot b \in \mathbb{N}$ множество $\mathbb{N}$ замкнуто относительно операций сложения и умножения
2. $a+b=b+a$, $a\cdot b=b\cdot a$ коммутативность
3. $(a+b)+c=a+(b+c)$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$ ассоциативность
4. $a\cdot (b+c)=a\cdot b+a\cdot c$ дистрибутивность
5. $a\cdot 1=a$ является нейтральным элементом для умножения

Поскольку множество $\mathbb{N}$ содержит нейтральный элемент для умножения, но не для сложения, добавление нуля к этому множеству обеспечивает включение в него нейтрального элемента для сложения.

Кроме этих двух операций, на множестве $\mathbb{N}$ определены отношения «меньше» ($

1. $a b$ трихотомия
2. если $a\leq b$ и $b\leq a$, то $a=b$ антисимметрия
3. если $a\leq b$ и $b\leq c$, то $a\leq c$ транзитивность
4. если $a\leq b$, то $a+c\leq b+c$
5. если $a\leq b$, то $a\cdot c\leq b\cdot c$

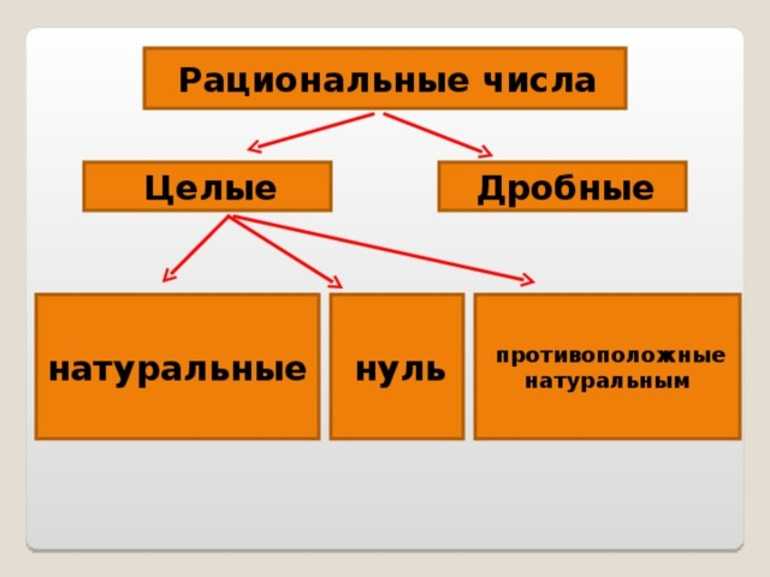
Рациональные числа

Когда у нас было 7 мешков по 6 килограмм, с помощью умножения мы легко посчитали, что общий вес содержимого мешков составляет 42 килограмма. Представим себе, что мы высыпали всё содержимое всех мешков в одну общую кучу массой 42 килограмма. А потом передумали, и захотели распределить содержимое обратно по 7 мешкам. Сколько килограмм при этом попадет в один мешок, если будем распределять поровну? – Очевидно, что 6.

А если захотим распределить 42 килограмма по 6 мешкам? Тут мы подумаем о том, что те же общие 42 килограмма могли бы получиться, если бы мы высыпали в кучу 6 мешков по 7 килограмм. И значит при делении 42 килограмм на 6 мешков поровну получим в одном мешке по 7 килограмм.

А если разделить 42 килограмма поровну по 3 мешкам? И здесь тоже мы начинаем подбирать такое число, которое при умножении на 3 дало бы 42. Для «табличных» значений, как в случае 6 ·7=42 => 42:6=7, мы выполняем операцию деления, просто вспоминая таблицу умножения. Для более сложных случаев используется деление в столбик, которое будет рассмотрено в одной из следующих статей. В случае 3 и 42 можно «подбором» вспомнить, что 3 ·14 = 42. Значит, 42:3=14. В каждом мешке будет по 14 килограмм.

Теперь попробуем разделить 42 килограмма поровну на 5 мешков. 42:5=?
Замечаем, что 5 ·8=40 (мало), а 5·9=45 (много). То есть, ни по 8 килограмм в мешке, ни по 9 килограмм, из 5 мешков мы 42 килограмма никак не получим. При этом понятно, что в реальности разделить любое количество (крупы, например,) на 5 равных частей нам ничего не мешает.

Операция деления целых чисел друг на друга не обязательно дает в результате целое число. Так мы пришли к понятию дроби. 42:5 = 42/5 = 8 целых 2/5 (если считать в обыкновенных дробях) или 42:5=8,4 (если считать в десятичных дробях).

Обыкновенные и десятичные дроби

Обыкновенные дроби хороши тем, что, чтобы представить такой дробью результат деления любых двух целых чисел, нужно просто записать делимое в числитель дроби, а делитель в знаменатель. (123:11=123/11, 67:89=67/89, 127:53=127/53, …) Затем по возможности сократить дробь и/или выделить целую часть (эти действия с обыкновенными дробями будут подробно рассмотрены в следующих статьях). Проблема в том, что производить арифметические действия (сложение, вычитание) с обыкновенными дробями уже не так удобно, как с целыми числами.

Для удобства записи (в одну строку) и для удобства вычислений (с возможностью вычислений в столбик, как для обычных целых чисел) кроме обыкновенных дробей придуманы ещё и десятичные дроби. Десятичная дробь – это специальным образом записанная обыкновенная дробь со знаменателем 10, 100, 1000 и т.п. Например, обыкновенная дробь 7/10 – это то же, что и десятичная дробь 0,7. (8/100 = 0,08; 2 целых 3/10=2,3; 7 целых 1/1000 = 7, 001). Переводу обыкновенных дробей в десятичные и наоборот будет посвящена отдельная статья. Операциям с десятичными дробями – другие статьи.

Любое целое число может быть представлено в виде обыкновенной дроби со знаменателем 1. (5=5/1; −765=−765/1).

Определение: Все числа, которые могут быть представлены в виде обыкновенной дроби, называют рациональными числами. Множество рациональных чисел обозначают буквой Q.

При делении любых двух целых чисел друг на друга (кроме случая деления на 0) всегда получим в результате рациональное число. Для обыкновенных дробей есть правила сложения, вычитания, умножения и деления, позволяющие произвести соответствующую операцию с любыми двумя дробями и получить в результате также рациональное число (дробь или целое).

Множество рациональных чисел – это первое из рассмотренных нами множеств, в котором можно и складывать, и вычитать, и умножать, и делить (кроме деления на 0), никогда не выходя за пределы этого множества (то есть, всегда получая в результате рационально число).

Казалось бы, других чисел не существует, все числа рациональные. Но и это не так.

Понятие рационального выражения

В и классе мы уже изучали дроби и действия над ними. В классе рассматривались рациональные числа, которые, по сути, и являются дробями. Однако до этого мы изучали только так называемые числовые дроби, у которых в числителе и знаменателе стоят какие-то числа либо выражения с числами, но не переменные величины.

Следующие дроби являются числовыми:

Однако нередко в алгебре приходится иметь дело и с дробями, которые содержат переменные. В качестве примера подобных выражений можно привести:

Так как деление на ноль является недопустимой операцией в алгебре, то некоторые дроби могут не иметь смысла. Так, дробь

бессмысленна, так как ее знаменатель 21 – 3•7 равен нулю.

Если дробь содержит переменные величины, то ее значение зависит от этих переменных. Так, дробь

при у = 4 принимает значение, равное 9. Если же у = 3, то эта дробь окажется бессмысленной.

Значения переменных величин, при которых дробь сохраняет свой смысл, называют допустимыми значениями переменных.

Пример. Укажите множество допустимых значений величин х и у для дроби

Решение. Недопустим только случай, при котором в знаменателе находится ноль, то есть когда выполняется равенство

х – у = 0

или равносильное ему равенство

х = у

Следовательно, допустимыми значениями являются все такие пары (х; у), что х ≠ у.

Пример. Каковы допустимые значения величин а и b в дроби

Решение. В данной записи есть три дробных черты, а значит, и три знаменателя:

Ни один из знаменателей не должен равняться нулю, поэтому

Перенесем в последнем неравенстве 2-ое слагаемое вправо, изменив знак (правила преобразований выражений со знаком ≠ точно такие же, как и у равенств):

По свойству пропорции имеем:

1•а ≠ 1•b

а ≠b

Итак, допустимыми являются все значения a и b, при которых а ≠ 0, b≠ 0, a≠b.

Пример. Найдите множество допустимых значений х для дроби

Решение.

Ясно, что знаменатель должен отличаться от нуля:

х2 – 25 ≠ 0

Чтобы найти, при каких значениях неизвестной величины знаменатель обращается в ноль, надо решить уравнение

х2 – 25 = 0

Представим полином в левой части как произведение, применив формулу квадрата разности:

х2 – 52= 0

(х – 5)(х + 5) = 0

х = 5 или х = – 5

Получаем, что исходная дробь сохраняет смысл при любых х, отличных от – 5 и 5.

Порою дроби, содержащие переменные, могут встречаться в тождествах.

Пример. Докажите тождество

Решение. У дроби в левой части знаменатель всегда положителен, поэтому все допустимыми являются все значения c. Согласно свойству операции деления, делимое равно произведению делителя и частного, поэтому для доказательства тождества надо лишь показать справедливость равенства

(с3 – 2с2 + с – 2) = (с – 2)(с2 + 1)

Раскроем скобки в правой части:

(с – 2)(с2 + 1) = с3 – 2с2 + с – 2

Получили одинаковое выражение и для левой, и для правой части тождества, следовательно, оно верное.

Теперь сформулируем понятие рационального выражения.

Среди рациональных выражений выделяют целые и дробные выражения.

Приведем примеры целых рациональных выражений:

А вот несколько примеров дробных рациональных выражений:

Стоит заметить, что дробь и дробное выражение – это два разных понятия. Для иллюстрации приведем два примера:

•  – это дробь, но целое, а не дробное выражение;
• (х + 7):t – это дробное выражение, но не дробь.

Отдельно отметим, что дробь равна нулю тогда, когда ее числитель равен нулю, а знаменатель нет. Если же и знаменатель равен нулю, то получается недопустимое действие – деление на ноль, поэтому дробь не будет иметь смысла.

Пример. Найдите все корни уравнения

Решение. На первый взгляд уравнение кажется сложным, особенно из-за знаменателя. Однако он здесь почти не играет роли. В левой части находится дробь, значит, нулю равен ее знаменатель:

(х – 1)(х + 2) = 0

х – 1 = 0 или х + 2 = 0

х = 1 или х = – 2

Получили два корня. Осталось убедиться, что при этих значениях х дробь не становится бессмысленной, то есть ее знаменатель не обращается в ноль. При х = 1 имеем знаменатель

2•14 – 3•13 + 5•1 – 4 = 2 – 3 + 5 – 4 = 0

поэтому число 1 НЕ является корнем уравнения. Теперь проверим знаменатель при х = – 2:

2•(– 2)4 – 3•( – 2)3 + 5•( – 2) – 4 =

= 32 + 24 – 10 – 4 = 42

Получается, что единственное корень уравнения – это ( – 2).

Ответ: – 2

Умножение рациональных чисел

Понятие числа расширяется от натуральных чисел к целым, а от целых чисел к рациональным. Это объясняет тот факт, что действия с целыми числами обладают всеми свойствами действий с натуральными числами. Следовательно, действия с рациональными числами должны обладать всеми свойствами действий с целыми числами. Однако для умножения рациональных чисел характерно еще одно свойство — свойство умножения взаимно обратных чисел.

С указанным принципом согласуются все перечисленные ниже правила умножения рациональных чисел.

Умножение на нуль

Начнем с правила умножения рационального числа на нуль: произведение любого числа a на нуль есть нуль. Запишем это утверждение в буквенном виде: a·0=0 для любого рационального числа a, а в силу переместительного свойства умножения это равенство можно переписать как 0·a=0.

Приведем примеры. Умножение рационального числа 5/12 на дает , произведение нуля и отрицательного рационального числа также равно нулю. В частности произведение нуля на нуль есть нуль, то есть, 0·0=0.

Умножение на единицу

Теперь озвучим правило умножения рационального числа на единицу: умножение любого рационального числа a на 1 в результате дает число a. То есть, a·1=a или 1·a=a, для любого рационального a. Таким образом, единица является нейтральным числом по умножению.

Например, умножение рационального числа 4,73 на 1 в результате дает 4,73. Другой пример: произведение равно .

Произведение взаимно обратных чисел

Если множители являются взаимно обратными числами, то их произведение равно единице. То есть, a·a−1=1.

Так произведение взаимно обратных чисел 7/8 и 8/7 равно единице. Аналогично, умножение −1,5 на −0,(6) в результате дает 1, так как −1,5=−3/2 и −0,(6)=−2/3, а −3/2 и −2/3 – взаимно обратные числа.

Умножение положительных рациональных чисел

В общем случае умножение положительных рациональных чисел можно свести к умножению обыкновенных дробей. Для этого множители нужно представить в виде обыкновенных дробей, если они сразу не являются таковыми.

Пример.

Вычислите произведение положительных рациональных чисел 0,4 и 5/28.

Решение.

Представим десятичную дробь 0,4 в виде обыкновенной дроби: 0,4=4/10=2/5. Таким образом, . Осталось выполнить умножение обыкновенных дробей: . На этом умножение исходных рациональных чисел завершено.

Вот все решение: .

Ответ:

.

Иногда удобно работать с конечными десятичными дробями, не выполняя переход к обыкновенным дробям.

Пример.

Вычислите произведение рациональных чисел вида 2,121·3,4.

Решение.

Здесь мы можем выполнить :

Ответ:

2,121·3,4=7,2114.

В частном случае умножение положительных рациональных чисел может собой представлять умножение натуральных чисел, или .

Пример.

Проведите умножение рациональных чисел 0,(1) и 3.

Решение.

Сначала переведем периодическую десятичную дробь в обыкновенную дробь: . Таким образом, от умножения исходных рациональных чисел 0,(1) и 3 ми переходим к умножению обыкновенной дроби 1/9 на 3. В итоге имеем .

Ответ:

.

Умножение рациональных чисел с разными знаками

Для умножения рациональных чисел с разными знаками применяется : надо умножить модули множителей и перед полученным числом поставить знак минус. Это правило позволяет от умножения рациональных чисел с разными знаками перейти к умножению положительных рациональных чисел, с которым мы разобрались в предыдущем пункте.

Рассмотрим решение примера.

Пример.

Выполните умножение отрицательного рационального числа на положительное рациональное число .

Решение.

По правилу умножения чисел с разными знаками имеем . Заменив смешанные числа соответствующими неправильными дробями, завершаем вычисления .

Ответ:

.

Умножение отрицательных рациональных чисел

Умножение отрицательных рациональных чисел сводится к умножению положительных чисел. При этом применяется следующее : нужно перемножить модули множителей.

Рассмотрим применение этого правила при решении примера.

Пример.

Выполните умножение отрицательных рациональных чисел −3,146 и −56.

Решение.

Модули множителей равны соответственно 3,146 и 56. Вычислим их произведение, для этого выполним умножение столбиком:

Таким образом, произведение исходных отрицательных рациональных чисел равно 176,176.

Ответ:

(−3,146)·(−56)=176,176.

Отрицательное значение перед рациональным числом

Рассмотрим простой пример:

(−6) : 2 = −3

В данном примере делимое равно  (−6)  и является отрицательным значением.

Далее можно рассмотреть иной пример. Составим и запишем выражение:

6 : (−2) = −3

В данном примере отрицательным является делитель равный (−2). Однако в двух случаях, при решении примеров, получается одинаковый ответ, который равен (−3). Данные примеры, также, можно записать в виде дробных значений.

Вид данных значений следующий \.

Так как в обоих случаях ответ, полученный при вычислении дробей, будет равным, то отрицательный знак, стоящий в числителе или в знаменателе можно вынести как общий. И тем самым, поставить его перед дробью:

\

Следовательно между дробями и \ и \ есть возможность поставить равенство, так как они имеют одинаковое значение \

Геометрическая интерпретация вещественных чисел.

Рассмотрим прямую l, выберем на ней начало отсчета (точку O) и масштабный отрезок OE длины 1. Числу 0 поставим в соответствие точку O, числу 1 — точку E, числу -1 — точку E’, симметричную точке E относительно точки O. Положительному числу α =a,a₁a₂…a_n… поставим в соответствие точку M, находящуюся справа от O на расстоянии α, а отрицательному числу β = b,b₁b₂…b_n… — точку M’, находящуюся слева от O на расстоянии |β|.

Эта прямая называется числовой прямой или числовой осью. Из аксиом геометрии и свойств вещественных чисел следует, что между множеством вещественных чисел \(\mathbb{R}\) и числовой прямой l устанавливается взаимно однозначное соответствие: каждому вещественному числу соответствует единственная точка числовой прямой и, наоборот, каждой точке числовой прямой соответствует некоторое вещественное число. Поэтому будем в дальнейшем будем отождествлять множество \(\mathbb{R}\) с множеством точек числовой прямой, а вещественные числа часто будем называть точками.

Условимся о следующих обозначениях для некоторых наиболее употребительных числовых множеств:

1. отрезок [a, b] ={x: a ≤ x ≤ b};
2. интервал (a, b) ={x: a < x < b};
3. полуинтервалы [a, b) = {x: a ≤ x < b}, (a, b] = {x: a < x ≤ b}.

Точки a и b называют концами отрезка, интервала, полуинтервала (a — левым концом, b — правым концом), отрезок [a, b], интервал (a, b), полуинтервалы [a, b) и (a, b] называют конечными промежутками (или промежутками), а точки x такие, что a < x < b, — их внутренними точками.

Наряду с конечными промежутками рассматривают также бесконечные промежутки:

интервалы

$$\left(a, \ +\infty \ \right)=\left\{x: \ x > a\right\} \ и \ \left(-\infty, \ a\right)=\left\{x: \ x < a\right\};\nonumber$$

полуинтервалы

$$\left=\left\{x: \ x \ \leqslant \ a\right\};\nonumber$$

\(\left(-\infty, \ +\infty\right)=\left\{x: \ x\in\mathbb{R}\right\}\) — множество вещественных чисел.

Напомним, что если каждый элемент множества A является элементом множества B, то пишут A ⊂ B или B ⊃ A и говорят, что A является подмножеством множества B. Например, \(\mathbb{J} \ \in \ \mathbb{R}\), \(\mathbb{Q} \ \in \ \mathbb{R}\).

Множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств A и B, называется объединением множеств A и B и обозначается A ∪ B.

Множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству A, так и множеству B, называется пересечением множеств A и B и обозначается A ∩ B.

Отметим, что

$$\mathbb{J} \ \cup \ \mathbb{Q} \ = \ \mathbb{R},\qquad\mathbb{J} \ \cap \ \mathbb{Q} \ = \ \varnothing,\nonumber$$

где ∅ — пустое множество, то есть множество, не содержащее элементов.

Если стоит минус

Когда школьники проходили тему умножения и деления, то им стало известно: в роли делителей и делимых могут выступать как отрицательные, так и положительные выражения.

Так, вариации 6:-2=-3 и -6:2=-3 имеют одинаковый результат, хотя знак минус имеют разные части.

Так как каждое деление можно представить в виде дроби, то минус ставится в числителе или в знаменателе. Либо сделать его общим.

Между всеми тремя вариациями можно поставить знак равенства, так как их результатом является одно и то же число.

Каждый из рациональных показателей имеет противоположное.

Перевод в дроби

Перевод смешанного выражения в неправильную дробь осуществляется с помощью умножения на знаменатель дробную часть и прибавить к числителю. Получившееся станет числителем новой дроби при прежнем знаменателе.

Рассматривать алгоритм можно на следующем простом примере:

• Имеется 2,5, которое следует перевести в неправильную дробь.
• Целый показатель нужно умножить на знаменатель дробной части и прибавить числитель этой же части.
• Полученное значение можно вычесть как (2*2)+1=4+1=5.
• 5 станет числителем, а знаменатель будет прежним и получится 5/2.
• Вернуть начальное смешанное можно выделением целой части.

Поэтому следует определить другой метод. Целая часть умножается на знаменатель дробной части. Из полученного значения вычитается числитель дробной части. И тогда получается правильный ответ.

Благодаря координатной прямой можно понять, почему смешанное -2,5 расположилось в левой части. Минус указывает на смещение влево в количестве двух шагов. Попадание произошло в точке -2. После чего сдвиг еще на полшага и середина между -3 и -2.

https://youtube.com/watch?v=42051qQzaZ0

Отношение рациональных чисел к другим классам чисел

Рациональные числа – это один из классов чисел в математике. Они относятся к классу действительных чисел и включают в себя все числа, которые могут быть представлены в виде обыкновенной дроби, где числитель и знаменатель являются целыми числами.

Отношение рациональных чисел к другим классам чисел может быть представлено следующим образом:

• Натуральные числа: Рациональные числа включают натуральные числа, так как любое натуральное число можно записать как дробь с знаменателем, равным 1.
• Целые числа: Рациональные числа включают целые числа, так как любое целое число можно записать как дробь, где знаменатель равен 1.
• Иррациональные числа: Рациональные числа не включают иррациональные числа, так как иррациональные числа не могут быть представлены в виде обыкновенной дроби.

Рациональные числа являются более широким классом чисел, чем натуральные и целые числа, но узким классом чисел по сравнению с действительными числами, которые включают иррациональные числа.

Вот некоторые особенности рациональных чисел:

1. Рациональные числа можно представить в виде десятичной дроби, которая может быть конечной или периодической.
2. Рациональные числа можно складывать, вычитать, умножать и делить друг на друга.
3. Рациональные числа образуют поле, что означает, что для любых двух рациональных чисел существуют операции сложения, вычитания, умножения и деления, которые дают другое рациональное число.

Рациональные числа играют важную роль в алгебре и математике в целом. Они используются для решения уравнений, проведения вычислений и в других различных областях науки и техники.

Целые числа $\mathbb{Z}$

Примеры целых чисел:
$1, -20, -100, 30, -40, 120…$

Решение уравнения
$a+x=b$, где $a$ и $b$ — известные натуральные числа, а $x$ — неизвестное натуральное число, требует введения новой операции — вычитания(-). Если существует натуральное число $x$, удовлетворяющее этому уравнению, то $x=b-a$. Однако, это конкретное уравнение не обязательно имеет решение на множестве $\mathbb{N}$, поэтому практические соображения требуют расширения множества натуральных чисел таким образом, чтобы включить решения такого уравнения. Это приводит к введению множества целых чисел: $\mathbb{Z}=\lbrace 0,1,-1,2,-2,3,-3…\rbrace$.

Поскольку $\mathbb{N}\subset \mathbb{Z}$, логично предположить, что введенные ранее операции $+$ и $\cdot$ и отношения $
1. $0+a=a+0=a$ существует нейтральный элемент для сложения
2. $a+(-a)=(-a)+a=0$ существует противоположное число $-a$ для $a$

Свойство 5.:
5. если $0\leq a$ и $0\leq b$, то $0\leq a\cdot b$

Множество $\mathbb{Z} $ замкнуто также и относительно операции вычитания, то есть $(\forall a,b\in \mathbb{Z})(a-b\in \mathbb{Z})$.

Комплексные числа$\mathbb{C}$

Примеры комплексных чисел:
$(1, 2), (4, 5), (-9, 7), (-3, -20), (5, 19),…$
$1 + 5i, 2 — 4i, -7 + 6i…$ где $i = \sqrt{-1}$ или $i^2 = -1$

Множество комплексных чисел представляет собой все упорядоченные пары действительных чисел, то есть $\mathbb{C}=\mathbb{R}^2=\mathbb{R}\times \mathbb{R}$, на котором операции сложения и умножения определены следующим образом:

$(a,b)+(c,d)=(a+b,c+d)$
$(a,b)\cdot (c,d)=(ac-bd,ad+bc)$

Существует несколько форм записи комплексных чисел, из которых самая распространенная имеет вид
$z=a+ib$, где $(a,b)$ — пара действительных чисел, а число $i=(0,1)$ называется мнимой единицей.

Легко показать, что $i^2=-1$. Расширение множества $\mathbb{R}$ на множество $\mathbb{C}$ позволяет определить квадратный корень из отрицательных чисел, что и послужило причиной введения множества комплексных чисел.
Также легко показать, что подмножество множества $\mathbb{C}$, заданное как $\mathbb{C}_0=\lbrace (a,0)|a\in \mathbb{R}\rbrace$, удовлетворяет всем аксиомам для действительных чисел, следовательно $\mathbb{C}_0=\mathbb{R}$, или $R\subset\mathbb{C}$.

Алгебраическая структура множества $\mathbb{C}$ относительно операций сложения и умножения имеет следующие свойства:
1. коммутативность сложения и умножения
2. ассоциативность сложения и умножения
3. $0+i0$ — нейтральный элемент для сложения
4. $1+i0$ — нейтральный элемент для умножения
5. умножение дистрибутивно по отношению к сложению
6. существует единственный обратный элемент как для сложения, так и для умножения.

Дробно-рациональные уравнения

А вот еще одно уравнение \( \displaystyle \frac+\frac-6>=3\).

Это уравнение целое? НЕТ. Тут есть деление на переменную \( \displaystyle x\), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.

На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.

Для начала найдем наименьший общий знаменатель, это будет \( \displaystyle (x+1)\cdot (x+3)\).

Важный момент!

В предыдущем примере, где было целое уравнение мы не стали свободный член \( \displaystyle 13\) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель \( \displaystyle (x+1)\cdot (x+3)\).

А это тебе не шутки, переменная в знаменателе!

Это надеюсь, ты запомнишь, но давай посмотрим что вышло:

Что-то оно огромное получилось, надо все посокращать:

\( \displaystyle 5(x+3)+(4-6)=3\cdot (x+1)\cdot (x+3)\).

Раскроем скобки и приведем подобные члены:

Ну как, это уже попроще выглядит, чем в начале было?

Выносим за скобку общий множитель: \( \displaystyle 3x\cdot (x+1)=0\)

У этого уравнения два решения, его левая сторона принимает нулевое значение при \( \displaystyle x=0\) и \( \displaystyle x=-1\).

Вроде бы все, ну ладно давайте напоследок подставим корни \( \displaystyle x=0\) и \( \displaystyle x=-1\) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим \( \displaystyle 0\), получается \( \displaystyle 3=3\) –нет претензий?

С ним все нормально. А теперь \( \displaystyle -1\), и тут же видим в знаменателе первого члена \( \displaystyle -1+1\)!

Но ведь это же будет ноль!

На ноль делить нельзя, это все знают, в чем же дело.

Дело в ОДЗ — Области Допустимых Значений!

Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.

Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:

ОДЗ: \( \displaystyle x+1\ne 0\) и \( \displaystyle x+3\ne 0\) \( \displaystyle \Rightarrow x\ne -1\) и \( \displaystyle x\ne -3\).

Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами \( \displaystyle x=0\) и \( \displaystyle x=-1\) мы смело исключаем \( \displaystyle x=-1\), т.к. он противоречит ОДЗ.

Значит, какой ответ будет у решенного уравнения?

В ответ стоит написать только один корень, \( \displaystyle x=0\).

Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.

Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,

Свойства рациональных чисел

Одно из основных свойств рациональных чисел — их замкнутость относительно всех арифметических операций.

Это свойство можно объяснить на примере натуральных чисел: 16+14=30. 30 — это натуральное число, как и его слагаемые. Это значит, что множество натуральных чисел замкнуто относительно операции сложения.

С помощью рациональных чисел можно выполнять любые арифметические операции:

• сложение: 3,5+2=5,5;
• умножение: \(-\frac45\cdot\frac54=-1\);
• вычитание: 1-7,6=-6,6;
• деление: \(3:8=\frac38\).

Таким образом, множество Q замкнуто относительно всех четырех операций.

Список свойств рациональных чисел широк. Его можно сократить до нескольких основных пунктов.

1. Упорядоченность. Между рациональными числами всегда можно идентифицировать один из видов отношений: «>», «<» или «=».
2. Транзитивность отношения порядка. Для любых трех рациональных чисел a, b, c верно следующее: если a<b, b<c, то a<c. Если a=b, b=c, то a=c.
3. Наличие противоположного числа. У любого рационального числа есть противоположное, при сложении с которым получается 0: a+(-a)=0.
4. Наличие обратного числа. Любое рациональное число имеет обратное ему число, при умножении на которое получается 1: \(\frac ab\cdot\frac ba=1\).
5. Аксиома Архимеда. Каким бы ни было рациональное число a, всегда можно взять столько единиц, что их сумма будет больше a: \(\sum_{k=1}^n1>a\)