Взаимно обратные числа

Приведение дробей к общему знаменателю

Представляешь, любые две дроби можно привести к общему знаменателю! Ну, если тебя это не поразило, ты, наверное, не понял о чем я. Вот смотри. Есть две дроби \( \displaystyle  1/3\) и \( \displaystyle  3/5\).

Тебе надо изменить эти дроби так, чтоб значение дробей не поменялось, но в знаменателе у обеих стало одно и то же число. Подскажу лишь, что для этого нужно воспользоваться основным свойством дроби.

Ладно, так и быть, покажу сам: \( \displaystyle  1/3=5/15\); \( \displaystyle  3/5=9/15\). Как ты видишь в знаменателе у обеих дробей \( \displaystyle  15\), и при этом, если сократить дроби, первую на \( \displaystyle  5\), а вторую на \( \displaystyle  3\), то получатся те же \( \displaystyle  1/3\) и \( \displaystyle  3/5\)!

Сказать, как это делается? Так и быть, тебе сегодня везет, читай ниже.

Свойства обратных чисел

Свойство №1

Обратное число существует для любого числа, кроме 0.

Ограничение связано с тем, что на 0 делить нельзя, и при определении обратного числа на ноль его придется один раз переносить в знаменатель, то есть фактически делить на него.

Свойство №2

Сумма пары взаимно обратных чисел всегда меньше 2. Математически это свойство можно выразить неравенством:

Недвижимость №3

умножение чисел на два взаимно обратных числа эквивалентно умножению на единицу. Математически:

Недвижимость №4

Числовые выражения могут быть выражены обратно.

Недвижимость № 5

Для имени, преднедного в виде программ с х прикрадим, обратным будет новым в виде программ с прикладем –х. Обоснование:

Это свойство означает, что обратное число также может быть выбрано для любой степени.

Даниил Романович | Просмотров: 3.4k

Как делить обыкновенные и десятичные дроби

Деление одной дроби на другую — это умножение её на вторую дробь в перевёрнутом виде

В отличие от сложения и вычитания, при делении неважно, какие у дробей знаменатели: одинаковые или разные. Просто умножьте числитель на числитель, а знаменатель на знаменатель и, если у вас получится неправильная дробь, выделите из неё целую часть

Например, вам нужно разделить 3 /₅ на 4 /₉. Для этого поменяйте местами числитель и знаменатель второй дроби — она превратится в 9 /₄ — и умножьте 3 /₅ на неё.

Если в примере изначально есть смешанные числа, как 1 7 /₂₀, сначала нужно перевести их в неправильные дроби (в данном случае получится 27 /₂₀), а потом делить, как описано выше.

На целое число

Чтобы разделить обыкновенную дробь на целое число, нужно представить его также в виде обыкновенной дроби: в числителе будет оно само, а в знаменателе единица. А затем делить как дробь на дробь. Например:

Можно действовать и ещё проще: умножить знаменатель на данное в примере число, а числитель оставить как есть.

А чтобы, наоборот, разделить целое число на обыкновенную дробь, нужно перевернуть эту дробь и умножить число на неё. Например:

Как делить десятичные дроби

На другую дробь

Это можно сделать двумя способами.

Первый — превратить десятичные дроби в обыкновенные. Например, 1,2 — это то же самое, что 1 2 /₁₀, или 12 /₁₀ в виде неправильной дроби, или 6 /₅ — если её сократить. Соответственно, процесс деления будет выглядеть так:

Теперь осталось перевести обыкновенную дробь обратно в десятичную. Для этого нужно умножить её на такое число, чтобы знаменатель получился кратным 10: 10, 100, 1 000 и так далее. В данном случае 4 /₅ умножаем на 2. Мы получим 8 /₁₀. Добавляем к этому нашу целую часть — 4 — и получаем итоговый результат 4,8.

Второй способ деления десятичных дробей — сначала превратить их в целые числа, а потом поставить запятую в получившемся результате.

• Найдите дробь, в которой больше всего знаков после запятой.
• Умножьте все дроби в примере на число, кратное 10, с таким же количеством нулей. Например, если у вас есть дробь 4,25 — это будет 100, а если 1,578 — 1 000.
• Разделите целые числа друг на друга столбиком.
• Отсчитайте слева направо столько знаков, сколько было добавлено нулей при умножении, и поставьте запятую.

Например: 7,44 ÷ 0,4 = (7,44 × 100) ÷ (0,4 × 100) = 744 ÷ 40 = 18,6.

На целое число

Десятичные дроби на целое число делите так же, как и обычные числа, столбиком. Когда в делимом (слева) закончится целая часть, поставьте запятую в частном (справа под чертой). Если делимое не удаётся разделить без остатка, добавляйте к нему нули, пока не получите конечный результат.

Шаги

1
Нахождение обратного числа для дроби или целого числа

1. 1
   Найдите обратное число для дробного числа, перевернув его.
   

   Например, обратным числом дроби 3 / 4 является 4 / 3
   .

   «Обратное число» определяется очень просто. Чтобы вычислить его, просто рассчитайте значение выражения «1 ÷ (исходное число).» Для дробного числа обратным числом является другое дробное число, которое можно вычислить просто «перевернув» дробь (поменяв местами числитель и знаменатель).

2. 2
   Запишите обратное число для целого числа в виде дроби.
   И в этом случае обратное число вычисляется, как 1 ÷ (исходное число). Для целого числа запишите обратное число в виде обычной дроби, не нужно производить вычисления и записывать его в виде десятичной дроби

   Например, обратное число для 2 равно 1 ÷ 2 = 1 / 2
   .

   .

2
Нахождение обратного числа смешанной дроби

1. 1
   Что такое «смешанная дробь».
   Смешанной дробью называется число, записанное в виде целого числа и простой дроби, например, 2 4 / 5 . Находжение обратного числа для смешанной дроби осуществляется в два этапа, описанных ниже.
2. 2
   Запишите смешанную дробь в виде неправильной дроби.
   Вы, конечно, помните, что единица может быть записана в виде (число)/(то же число), а дроби с одинаковым знаменателей (числом под чертой) можно сложить друг с другом. Вот как это можно сделать для дроби 2 4 / 5:
   • 2 4 / 5
   • = 1 + 1 + 4 / 5
   • = 5 / 5 + 5 / 5 + 4 / 5
   • = (5+5+4) / 5
   • = 14 / 5 .
3. 3
   Переверните дробь.
   

   Для вышеприведенного примера обратное число будет равно 14 / 5 — 5 / 14
   .

   Когда смешанная дробь записана в виде неправильной дроби, мы можем легко найти обратное число, просто поменяв местами числитель и знаменатель.

3
Нахождение обратного числа для десятичной дроби

1. 1
   Если это возможно, выразите десятичную дробь в виде простой дроби.
   

   Например, обратное число для 0,5 равно 2 / 1 = 2.

   Вам нужно знать, что многие десятичные дроби можно легко превратить в простые дроби. Например, 0,5 = 1 / 2 , а 0,25 = 1 / 4 . Когда вы записали число в виде простой дроби, то сможете легко найти обратное число, просто перевернув дробь.

2. 2
   Решите задачу с помощью деления.
   

   Например, обратное число для 0,4 рассчитывается как 1 ÷ 0,4.

   Если вы не можете записать десятичную дробь в виде простой дроби, рассчитайте обратное число, решив задачу делением: 1 ÷ (десятичная дробь). Для решения вы можете воспользоваться калькулятором или перейти к следующему шагу, если хотите рассчитать значение вручную.

3. 3
   Измените выражение, чтобы работать с целыми числами.
   Первый шаг в деление десятичной дроби — это перемещение позиционной запятой до тех пор, пока все числа в выражении не станут целыми числами. Поскольку вы перемещаете позиционную запятую на одинаковое количество знаков, как в делимом, так и в делителе, вы получаете правильный ответ.
4. 4
   Например, вы берете выражение 1 ÷ 0,4 и записываете его как 10 ÷ 4.
   В этом случае вы переместили запятую на один знак вправо, что равносильно тому, если бы вы умножили каждое число на десять.
5. 5
   Решите задачу, разделив числа столбиком.
   С помощью деления столбиком вы сможете рассчитать обратное число. Если вы разделите 10 на 4, у вас должно получиться 2,5, что и будет обратным числом для 0,4.

• Значение отрицательного обратного числа будет равно обратному числу, умноженному на -1. Например, отрициательное обратное число для 3 / 4 равно — 4 / 3 .
• Обратное число иногда называют «обратным значением» или «обратной величиной».
• Число 1 является своим собственным обратным числом, поскольку 1 ÷ 1 = 1.
• Ноль не имеет обратного числа, поскольку выражение 1 ÷ 0 не имеет решений.

Пара чисел, произведение которых равно единице, называются взаимно обратными
.

Примеры: 5 и 1/5, −6/7 и −7/6, и

Для всякого числа а, не равного нулю , существует обратное 1/a.

Обратной величиной нуля является бесконечность.

Обратные дроби
— это две дроби, произведение которых равно 1. Например, 3/7 и 7/3; 5/8 и 8/5 и т. д.

Несократимые и сократимые дроби

Если наибольший общий делитель числителя и знаменателя дроби равен единице, то дробь называется несократимой. Например: .

суть несократимые дроби.

Если же наибольший общий делитель числителя и знаменателя отличен от единицы, то дробь называется сократимой. Например:

суть сократимые дроби.

Если числитель или знаменатель дроби отдельно или одновременно являются многочленами, то для решения вопроса о сократимости или несократимости этой дроби необходимо эти многочлены предварительно разложить на целые неприводимые множители, если это возможно. Например, дробь сократима, так как после разложения числителя и знаменателя на множители она принимает вид

Если числитель и знаменатель дроби разделить на их наибольший общий делитель, то получится . несократимая дробь, тождественно равная данной дроби.

Примеры сокращения дробей:

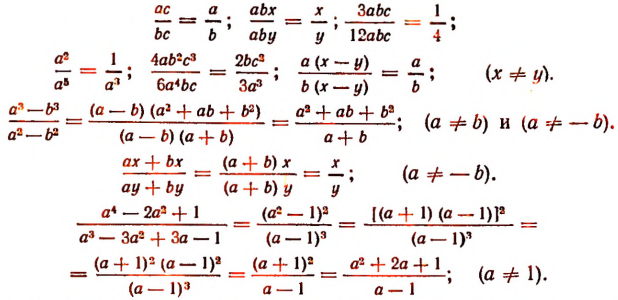
Сократить дробь — это значит разделить числитель и знаменатель этой дроби на какой-нибудь их общий множитель.

Полученная после этого новая дробь будет тождественно равна первоначальной дроби. Например,

(Здесь дробь сокращена только на общий множитель b.)

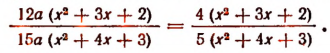
(Здесь дробь сокращена только на За.)

Примечание:

Выражение по форме дробное, но по существу целое, так как оно тождественно равно выражению 5аb. Однако между выражениями и 5ab имеется еще и другое различие, а именно выражение при а = 0 смысла не имеет, тогда как выражение 5ab при а = 0 имеет смысл, так как принимает определенное значение нуль.

Что делать, если у дроби есть целая часть

Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.

Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:

1. Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
2. Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
3. Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.

Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:

Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:

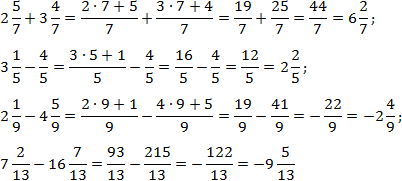
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.

Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.

Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.

Обратное число

Обра́тное число́ (обратное значение, обратная величина) — это число, на которое надо умножить данное число, чтобы получить единицу. Пара чисел, произведение которых равно единице, называются взаимно обратными.

Примеры: 5 и 1/5, −6/7 и −7/6, и

Для всякого числа а, не равного нулю, существует обратное 1/a.

Обратной величиной нуля является бесконечность.

Обратные дроби — это две дроби, произведение которых равно 1. Например, 3/7 и 7/3; 5/8 и 8/5 и т. д.

См. также

• Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).
• Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.

Теория чисел

Wikimedia Foundation . 2010 .

Смотреть что такое «Обратное число» в других словарях:

ОБРАТНОЕ ЧИСЛО — число, произведение которого на данное число равно единице. Два таких числа называются взаимно обратными. Таковы, напр., 5 и 1/5, 2/3 и 3/2 и т. д … Большой Энциклопедический словарь

обратное число — — Тематики энергетика в целом EN inverse numberreciprocal number … Справочник технического переводчика

обратное число — число, произведение которого на данное число равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 и 1/5, 2/3 и 3/2 и т. д. * * * ОБРАТНОЕ ЧИСЛО ОБРАТНОЕ ЧИСЛО, число, произведение которого на данное число равно… … Энциклопедический словарь

Обратное число — число, произведение которого с данным числом равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 и а, не равного нулю, существует обратное … Большая советская энциклопедия

ОБРАТНОЕ ЧИСЛО — число, произведение к рого на данное число равно единице. Два таких числа наз. взаимно обратными. Таковы, напр., 5 и 1/5. 2/3 и 3/2 и т. д … Естествознание. Энциклопедический словарь

Число — У этого термина существуют и другие значения, см. Число (значения). Число  основное понятие математики, используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей… … Википедия

Число (матем.) — см. также: Число (лингвистика) Число абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое … Википедия

Обратное закручивание воды при стоке — Обратное закручивание воды при стоке  околонаучный миф, основанный на неверном применении эффекта Кориолиса к движению воды в водовороте, возникающему при её стоке в сливное отверстие раковины или ванны. Суть мифа состоит в том, что вода… … Википедия

ЧИСЛО ИРРАЦИОНАЛЬНОЕ — ЧИСЛО, ИРРАЦИОНАЛЬНОЕ, число, которое не может быть выражено в виде дроби. Примеры включают Ц2 и число p. Следовательно, иррациональные числа это числа с бесконечным числом (непериодических) знаков после запятой. (Однако обратное не является… … Научно-технический энциклопедический словарь

Обратное преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия

Выделение целой части неправильной рациональной дроби

Выражение

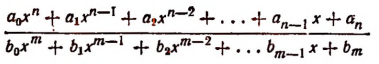
называется рациональной дробью.

Если , то эта дробь называется неправильной; в противном случае, т. е. когда , она называется правильной.

Например, рациональные дроби

являются неправильными.

Рациональные дроби

являются правильными.

Выделение целой части

Пусть требуется выделить целую часть неправильной рациональной дроби, например дроби

Разделим многочлен на многочлен

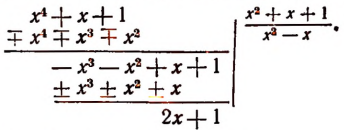
Получили частное и остаток

Делимое равно делителю, умноженному на частное плюс остаток. Поэтому

Разделив левую и правую части этого тождества на получим

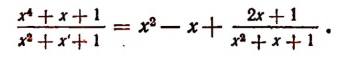
Выражение называется целой частью дроби выражение же есть правильная дробь.

Таким образом, неправильная рациональная дробь

оказалась представленной в виде суммы многочлена и правильной дроби .

Изложенное преобразование применимо ко всякой неправильной рациональной дроби.

В курсе высшей математики встречаются задачи, для решения которых необходима операция выделения целой части неправильной рациональной дроби.

Примеры:

1. Выделить целую часть неправильной рациональной дроби

т. е. представить эту дробь в виде алгебраической суммы целого многочлена и правильной рациональной дроби.

Отв.

2. Выделить целую часть дроби

3. Выделить целую часть дроби

Отв.

О символах и

1. О символе

Символ по своей форме напоминает степень. Однако истолковать его как степень в первоначальном понимании этого слова, т. е. как произведение, составленное из одинаковых множителей, невозможно. Бессмысленно сказать, что число а умножается само на себя нуль раз. С этой точки зрения выражение ие имеет смысла. Но если мы хотим расширить правило деления степеней и на тот случай, когда их показатели одинаковые, то нам достаточно принять по условию символ , где , равным единице.

Итак, примем по определению, что , если только . Тогда

Выражение же остается лишенным смысла. Теперь мы можем писать

где . И эта запись будет вполне оправдана. В самом деле, левая часть есть единица, так как делимое и делитель равны между собой и отличны от нуля. Правая часть согласно принятому определению также есть единица.

2. О символе

Символ также имеет форму степени. Однако истолковать его как степень в первоначальном понимании этого слова невозможно. Бессмысленно говорить, что число а умножается само на себя отрицательное число раз. Но если мы хотим расширить правило деления степеней и на тот случай, когда показатель степени делимого меньше показателя степени делителя, достаточно принять , где , равным

Итак, примем по определению, что , где .

Тогда

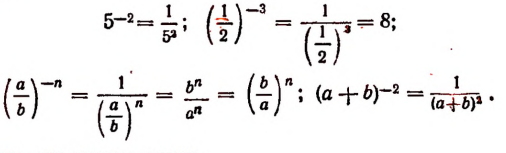
Теперь мы можем писать

где .

И эта запись будет вполне оправданной. В самом деле, левая часть есть , т. е. правая же, по принятому нами определению, также есть .

3. Действия над символами и

Хотя символы и не являются степенями в первоначальном смысле этого слова, однако оказывается, что над ними можно производить действия по тем же самым правилам, которые были установлены для степеней с натуральными показателями. В самом деле, докажем, например, что равенство

является верным.

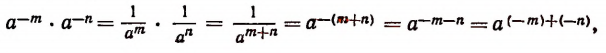
что и требовалось доказать.

Также легко убедиться в справедливости и такого равенства

Действительно,

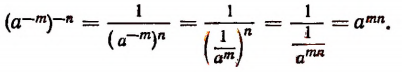
Все это позволяет нам символы и называть степенями.

Символ называется степенью с нулевым показателем, символ — степенью с отрицательным показателем.

Теперь мы можем равенство

где , считать справедливым при любых целых значениях букв тип.

Примеры:

Очевидно, что

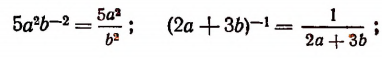
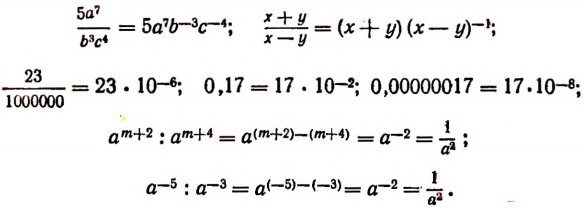
Общие сведения

Смешанная дробь — число, состоящее из целого значения и обыкновенного дробного выражения. Они образуются в результате операции деления. Последняя состоит из трех элементов, а именно: делимого, делителя и частного. Чтобы понять смысл смешанного числа, нужно разобрать дробные величины. К ним относятся следующие виды:

1. Обыкновенные.
2. Десятичные.

Обыкновенная дробь образуется посредством комбинации делимого и делителя, т. е. состоит всего из двух элементов. В этом случае частное имеет вид десятичного дробного тождества. Иными словами, десятичная дробь — величина, полученная при делении числителя на знаменатель.

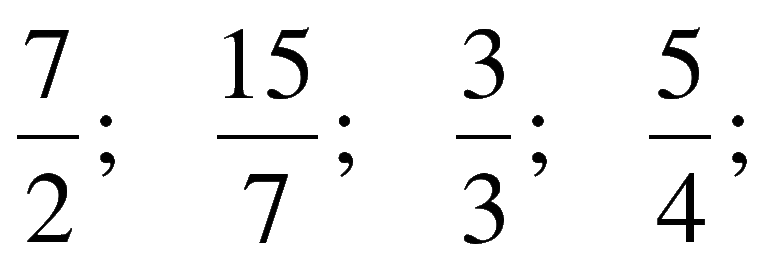
Обыкновенные дробные выражения бывают двух видов: правильными и неправильными. У первых величина числителя меньше знаменателя, а у вторых — наоборот. Десятичные дроби делятся на 3 типа: с фиксированным количеством знаков после запятой, бесконечные периодические и непериодические.

У периодических дробных величин после запятой математические символы повторяются через определенный период, который указывается в круглых скобках. Например, число 4,(3) читается следующим образом: четыре целых и три в периоде.

Следует отметить, что бесконечные непериодические дробные выражения в их полном виде невозможно записать на листе бумаги, поскольку количество разрядов достигает бесконечности. Далее необходимо рассмотреть сокращение дробей, поскольку операция применяется для оптимизации конвертации неправильного дробного тождества в смешанное число.

Свойства дробей

Дроби, как и любые числовые выражения, обладают определенными свойствами. К ним относятся:

1. Если от числителя отнять одно значение, а затем его прибавить, дробь не изменится, т. е. (Q+T-T)/Z=Q/Z.
2. При умножении и делении на эквивалентное число величина дробного тождества не изменится, т. е. (Q*T)/(Z*Т)=Q/Z.

Первое утверждение проверить очень просто. Для этой цели нужно решить следующий пример, прибавив и отняв от числителя одно и то же значение: 7/8. Доказательство имеет такой вид:

1. Записать дробь: 7/8.
2. Взять произвольный коэффициент: 5.
3. Отнять, а затем прибавить его к числителю: (7−5+5)/8.
4. Числа «-5» и «5» являются противоположными. Их сумма равна 0, т. е. 5−5=0.
5. Если прибавить нуль к любому числу, получится искомая величина: 5+0=5.
6. Математические преобразования исходной дроби: (7−5+5)/8=/8=(7+0)/8.
7. Результат совпадает с искомым значением: 7/8=7/8.

Второе утверждение доказывается таким же простым способом на дроби ½. Для этого нужно решить пример (1*8)/(2*8) по следующему нестандартному алгоритму:

1. Записать дробное тождество: ½.
2. Коэффициент — общий множитель: 8. Последний необходимо представить в виде обыкновенной дроби: 8/8.
3. Величина «8/8» эквивалентна единице, которую можно умножить на любое число без потери значения выражения.
4. Расписать дробное значение: (½) * (8/8) = (½) * 1 = ½.
5. Сравнить результат и исходное значение: ½ = ½.
6. Утверждение доказано.

Некоторые ученики делают большую ошибку, отнимая (прибавляя) к числителю и знаменателю одну величину. Чтобы они не путали 2 утверждения сокращения, нужно привести пример и решить его:

1. Записать искомое значение: ½.
2. Коэффициент: 3.
3. Прибавить значение «3» к числителю и знаменателю: (1+3)/(2+3)=4/5.
4. Превратить искомое значение и величину в третьем пункте в десятичные дроби: 0,5 и 0,8.
5. Сравнить: 0,5 < 0,8.

Упрощение выражений

Преобразование любого арифметического выражения начинается с упрощения. Последнее применяется для уменьшения расчетов, при которых возникают ошибки. Упростить выражение — значит, сделать его более читабельным и предоставить возможность дальнейшего применения при расчетах. Иными словами, каждый результат должен «подгоняться» под мировой стандарт. Для сокращения дробей обыкновенного типа рекомендуется использовать такие правила:

1. Вынесения общего множителя за скобки и сокращение на него.
2. Формулы сокращенного умножения.
3. Приведение подобных слагаемых.

Первое правило позволяет найти единый множитель всего дробного выражения. После этого его можно будет разделить на одно и то же число. Формулы сокращенного умножения применяются также для реализации первого правила. Суть метода заключается в использовании специальных соотношений. Например, математическое выражение «1−25t 2 » выглядит таким образом: (1−5t)(1+5t).

После раскрытия скобок реализовывается третье правило — приведение подобных слагаемых. Они группируются по наличию однотипных элементов. Например, выражение 4t-4+t+t 2 −3+2t 2 имеет следующие одинаковые компоненты, которые группируются в скобках: (2t 2 +t 2 )+(4t+t)-(4+3). Если приводить подобные элементы, выражение упрощается, т. е. 3t 2 +5t-7.

Деление дроби на число

Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?

Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет  пиццы. Значит каждому достанется по  пиццы.

Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.

Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.

Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.

Итак, требуется разделить дробь  на число 2. Здесь делимым является дробь , а делителем число 2.

Чтобы разделить дробь  на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить  на 

Получили ответ . Значит при делении половины на две части получается четверть.

Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:

Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:

Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:

Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь 

В обоих случаях получился один и тот же результат.

Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить  на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь 

Пример 2. Найти значение выражения 

Умножим первую дробь на число, обратное делителю:

Допустим, имеется четверть пиццы и нужно разделить её на двоих:

Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:

Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5

10 : 2 = 5

Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь 

Как видно результат не изменился. Мы снова получили ответ 5.

Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.

Пример 3. Найти значение выражения 

Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь 

Допустим, имелось  пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков

Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении  на 6 получается 

Задачи с обратными дробями

Обратные дроби широко используются в математике и повседневной жизни. Рассмотрим некоторые задачи, в которых требуется использовать обратные дроби.

1. Определение скорости

   Для определения скорости движения тела используется отношение пройденного пути к затраченному времени:

   Скорость = Пройденный путь / Время

   Если пройденный путь равен 50 км, а время, затраченное на его прохождение, равно 2 часам, то скорость будет:

   Скорость = 50 км / 2 ч = 25 км/ч

   Таким образом, скорость можно представить в виде обратной дроби.

2. Расчет времени выполнения работы

   Если известны объем работы и производительность рабочего, то время, необходимое для выполнения работы, можно рассчитать по формуле:

   Время = Объем работы / Производительность

   Например, если объем работы составляет 100 единиц, а производительность рабочего равна 10 единиц в час, то время выполнения работы будет:

   Время = 100 единиц / 10 единиц/ч = 10 часов

   В данном случае, время также представляет собой обратную дробь.

3. Расчет концентрации раствора

   Для расчета концентрации раствора используется отношение массы растворенного вещества к объему раствора:

   Концентрация = Масса / Объем

   Например, если масса растворенного вещества равна 10 г, а объем раствора равен 100 мл, то концентрация раствора будет:

   Концентрация = 10 г / 100 мл = 0.1 г/мл

   Таким образом, концентрация представляет собой обратную дробь.

Во всех этих задачах обратные дроби являются неотъемлемой составляющей и помогают определить отношения и соотношения между различными значениями.

Определение взаимно обратных чисел

С предыдущих уроков математики мы знаем: если прибавить или вычесть из числа нуль — оно не изменится. Точно также, если умножить или разделить число на единицу.

Ноль — нейтральный элемент для сложения и вычитания. При этом числа, которые в сумме дают ноль, называют противоположными.

Например: 2 + (-2) = 0.

Единица — нейтральный элемент для умножения и деления. Поэтому симметричными называют числа, чье произведение дает единицу.

Например: 3/5 * 5/3 = 1.

Два числа называют взаимно обратными, если их произведение равно 1.

Обратное число к данному числу — это такое число, которое мы умножаем на данное число и получаем единицу.

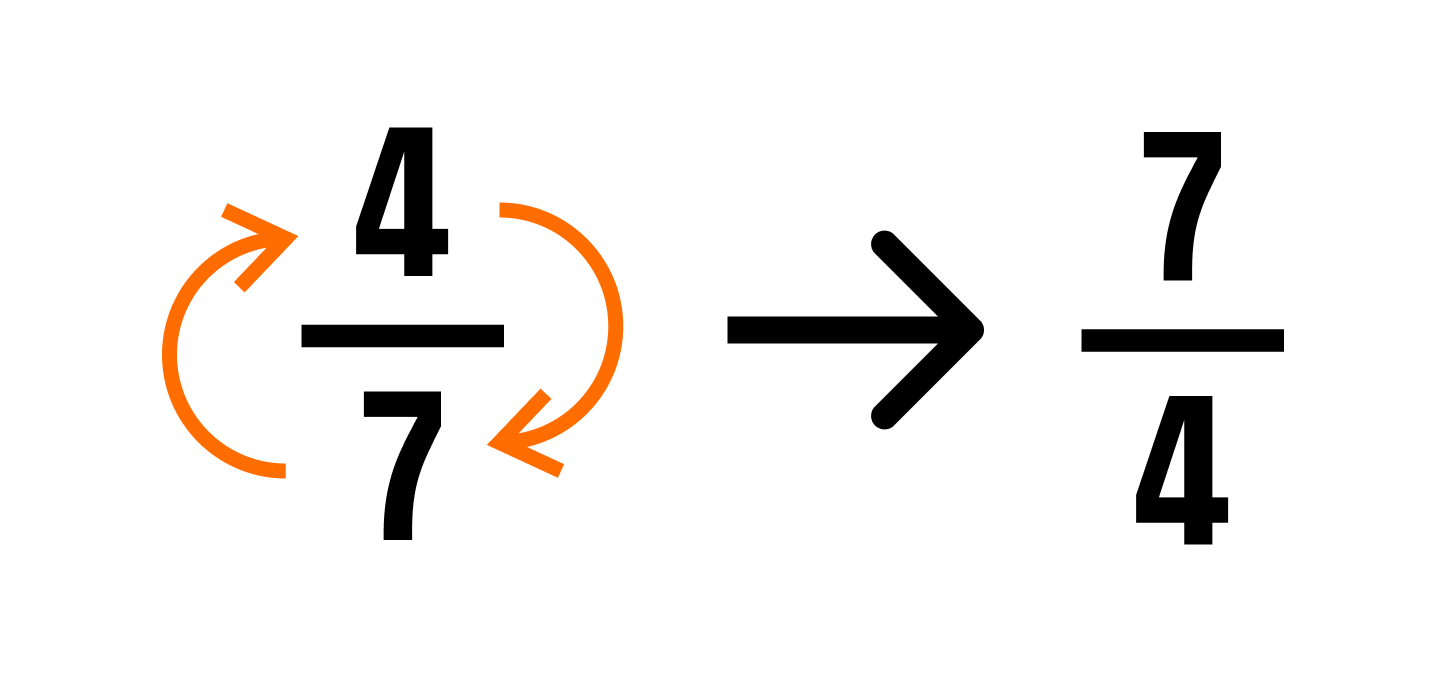
Если числа a и b взаимно обратные, то можно сказать, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Также можно говорить, что числу a обратно число b, а числу b обратно число a.

Приведем примеры взаимно обратных чисел. Так как произведение двух единиц равно 1, то по определению числа 1 и 1 — взаимно обратные.

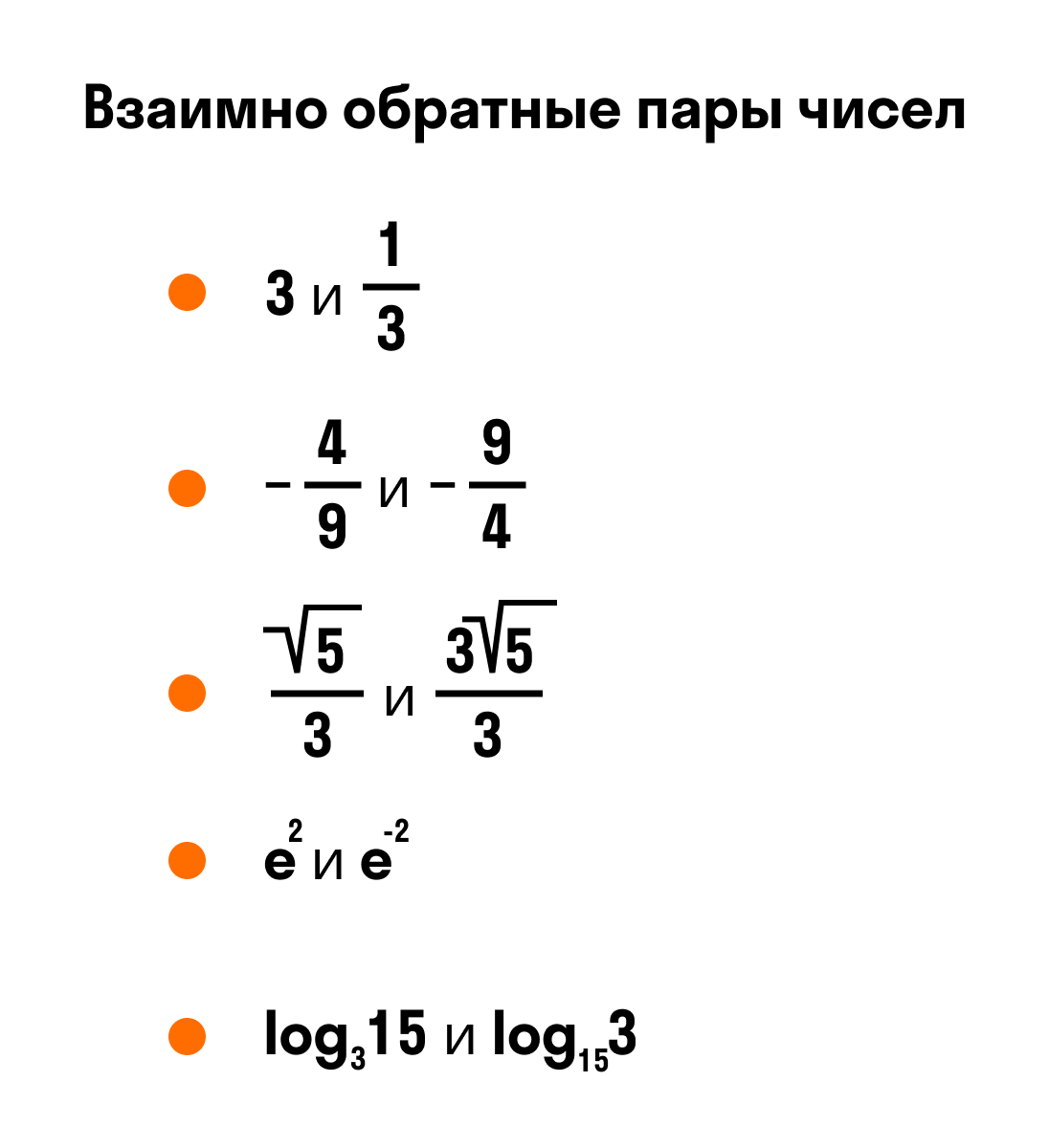
Определение взаимно обратных чисел относится к любым числам — натуральным, целым, действительным, комплексным.

Десятичная точка в дробях

Запятую в десятичной дроби, которая отделяет целую часть от дробной, по-другому называют десятичной точкой.

Дело в том, что в некоторых источниках целая часть от дробной отделяется именно точкой, а не запятой. Например:

2.5 (две целых пять десятых)

15.65 (пятнадцать целых шестьдесят пять сотых)

Точка часто используется для записи десятичных дробей на компьютере — в программировании и при работе в математических пакетах. В остальных случаях: на письме и при подготовке документов, в десятичных дробях чаще используется запятая, а не точка.

Мы используем в десятичных дробях запятую, а не точку, поэтому разумнее называть эту запятую десятичной запятой.

Но десятичную запятую большинство людей тоже называют десятичной точкой. Что в принципе не является ошибкой, потому как речь всё равно идёт о разделителе, котором отделяет целую часть от дробной.

Давайте и мы будем называть свою запятую в десятичных дробях десятичной точкой. Это словосочетание проговаривается легче и приятнее на слух.

Десятичная точка используется для увеличения или уменьшения дроби в 10, 100, 1000 и более раз. При увеличении десятичной дроби, десятичная точка передвигается вправо, а при уменьшении — влево. Чтобы быстро запомнить это, можно воспользоваться фразами «чем правее, тем больше» и «чем левее, тем меньше».

Пример 1. Увеличить десятичную дробь 6,3 в десять раз.

Чтобы увеличить десятичную дробь 6,3 в десять раз, достаточно передвинуть десятичную точку вправо на одну цифру, получим 63.

Пример 2. Уменьшить десятичную дробь 6,3 в десять раз.

Для уменьшения дроби 6,3 в десять раз достаточно передвинуть десятичную точку влево на одну цифру, получим 0,63

На вопрос «как узнать на сколько цифр передвигать десятичную точку?», нужно смотреть во сколько увеличивается (или уменьшается) десятичная дробь. Если дробь нужно увеличить (или уменьшить) в десять раз, то десятичная точка сдвигается на одну цифру.

Если дробь нужно увеличить (или уменьшить) в сто раз, то десятичная точка сдвигается на две цифры.

Если дробь нужно увеличить (или уменьшить) в тысячу раз, то десятичная точка сдвигается на три цифры. В общем, всё зависит от количества нулей во множителе.

Например, увеличить дробь в десять раз означает умножить её на 10. Мы помним, что для того чтобы умножить десятичную дробь на 10, нужно в этой дроби передвинуть запятую вправо на одну цифру (поскольку в числе 10 один ноль). Теперь можно не заучивать подобные правила. Такое умножение можно легко выполнить, передвинув десятичную точку.

Пример 3. Увеличить десятичную дробь 6,3 в тысячу раз.

Чтобы увеличить десятичную дробь 6,3 в тысячу раз, достаточно передвинуть десятичную точку вправо на три цифры, получим 6300. Если после запятой не хватает цифр, то вместо недостающих цифр записывают нули, что мы и сделали.

Пример 4. Уменьшить десятичную дробь 12,5 в сто раз.

Для уменьшения дроби 12,5 в сто раз, достаточно передвинуть десятичную точку влево на две цифры, получим 0,125

Десятичную точку можно использовать не только в десятичных дробях. Её можно использовать для увеличения (уменьшения) и других чисел в 10, 100 или в 1000 раз.

Возьмём к примеру целое число 325 и поставим в конце точку, получим 325 с точкой. Воспользуемся в этот раз точкой, так как её легче изобразить на рисунке:

Попробуем уменьшить это число в десять раз. Для этого достаточно будет передвинуть точку влево на одну цифру, получим 32.5

Попробуем увеличить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры вправо, получим 123000.

Попробуем уменьшить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,123

Попробуем уменьшить число 65 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,065

Попробуем увеличить число 65 в сто раз. Для этого достаточно передвинуть десятичную точку на две цифры вправо, получим 6500.

Определение обратных чисел

Обратными числами называются числа, которые при умножении друг на друга дают единицу. Такие числа обладают специальными свойствами и находят применение в различных областях математики, физики и других наук.

Для обратного числа существует определенное правило: обратное число a обозначается как 1/a или a^(-1)

Важно отметить, что обратное число существует только для ненулевых чисел, поскольку деление на ноль не имеет смысла и не определено

Обратное число отличается от обратного элемента. В математических структурах, таких как группы или поля, обратный элемент – это элемент, который, при определенной операции, примененной к нему и другому элементу множества, дает единичный элемент. Обратные числа – это частный случай обратных элементов, где операцией является умножение.

Обратные числа являются важным понятием в математике и используются в различных областях, таких как решение уравнений, матричные операции, геометрия и др. Знание обратных чисел позволяет более эффективно решать различные задачи и находить рациональные решения.