Таблицы синусов, косинусов, тангенсов и котангенсов

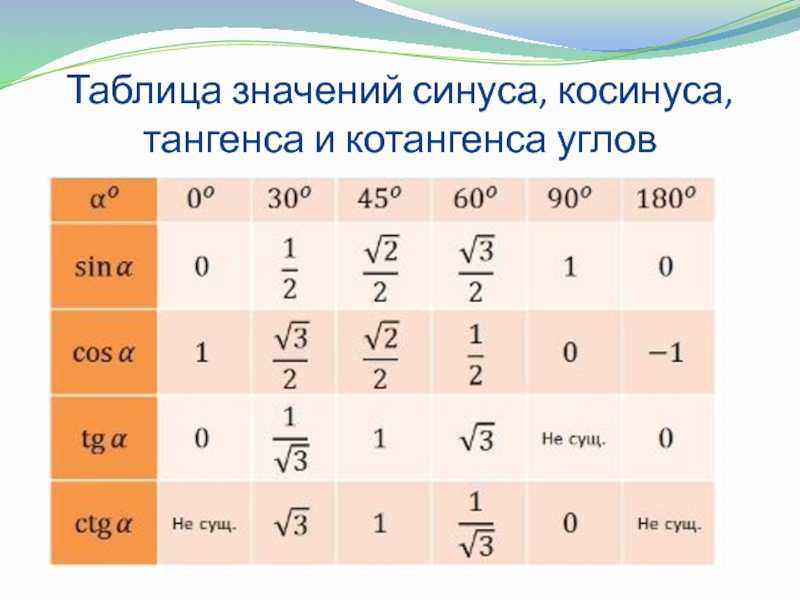
Свойства тригонометрических функций: синус и косинус

Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.

Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:

Синусоида	Косинусоида
y = sin x	y = cos x
ОДЗ	ОДЗ
sin x = 0, при x = πk, где k ϵ Z	cos x = 0, при x = π/2 + πk, где k ϵ Z
sin x = 1, при x = π/2 + 2πk, где k ϵ Z	cos x = 1, при x = 2πk, где k ϵ Z
sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z	cos x = — 1, при x = π + 2πk, где k ϵ Z
sin (-x) = — sin x, т. е. функция нечетная	cos (-x) = cos x, т. е. функция четная
функция периодическая, наименьший период — 2π	функция периодическая, наименьший период — 2π
sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk)	cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk)
возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk]	возрастает на промежутке
убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk]	убывает на промежутках
производная (sin x)’ = cos x	производная (cos x)’ = — sin x

Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.

Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:

Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.

Тригонометрия в геометрии

Во многих задачах по геометрии часто удобно использовать тригонометрию для нахождения углов или сторон треугольника. Даже одни из самых мощных теорем в курсе школьной геометрии называются теорема косинусов и теорема синусов. Это нам как бы намекает на тесную связь этих двух разделов математики. И определение тригонометрических функций в 9-м классе дается через геометрическую фигуру — прямоугольный треугольник.

Попробуем теперь порешать классические задачи геометрии с использованием тригонометрии:

Пример 5Дан прямоугольный треугольник $\bigtriangleup{ABC}$, в котором угол $\angle{C}=90^o$, угол $\angle{A}=60^o$, сторона $AC=5$. Найти все стороны треугольника $\bigtriangleup{ABC}$.

Таблица котангенсов

Котангенсом угла называется отношение косинуса этого угла к синусу:

Таблица котангенсов — таблица, содержащая значения котангенсов углов. В нашей таблице вычислены котангенсы углов от 1° до 180°.

Таблицы котангенсов удобно использовать при отсутствии калькулятора с тригонометрическими функциями.

См. также: таблица синусов, таблица косинусов, таблица тангенсов.

Таблица котангенсов углов от 1° до 90°

ctg(1°) = 57.289962
ctg(2°) = 28.636253
ctg(3°) = 19.081137
ctg(4°) = 14.300666
ctg(5°) = 11.430052
ctg(6°) = 9.514364
ctg(7°) = 8.144346
ctg(8°) = 7.115370
ctg(9°) = 6.313752
ctg(10°) = 5.671282
ctg(11°) = 5.144554
ctg(12°) = 4.704630
ctg(13°) = 4.331476
ctg(14°) = 4.010781
ctg(15°) = 3.732051
ctg(16°) = 3.487414
ctg(17°) = 3.270853
ctg(18°) = 3.077684
ctg(19°) = 2.904211
ctg(20°) = 2.747477
ctg(21°) = 2.605089
ctg(22°) = 2.475087
ctg(23°) = 2.355852
ctg(24°) = 2.246037
ctg(25°) = 2.144507
ctg(26°) = 2.050304
ctg(27°) = 1.962611
ctg(28°) = 1.880726
ctg(29°) = 1.804048
ctg(30°) = 1.732051

ctg(31°) = 1.664279
ctg(32°) = 1.600335
ctg(33°) = 1.539865
ctg(34°) = 1.482561
ctg(35°) = 1.428148
ctg(36°) = 1.376382
ctg(37°) = 1.327045
ctg(38°) = 1.279942
ctg(39°) = 1.234897
ctg(40°) = 1.191754
ctg(41°) = 1.150368
ctg(42°) = 1.110613
ctg(43°) = 1.072369
ctg(44°) = 1.035530
ctg(45°) = 1
ctg(46°) = 0.965689
ctg(47°) = 0.932515
ctg(48°) = 0.900404
ctg(49°) = 0.869287
ctg(50°) = 0.839100
ctg(51°) = 0.809784
ctg(52°) = 0.781286
ctg(53°) = 0.753554
ctg(54°) = 0.726543
ctg(55°) = 0.700208
ctg(56°) = 0.674509
ctg(57°) = 0.649408
ctg(58°) = 0.624869
ctg(59°) = 0.600861
ctg(60°) = 0.577350

ctg(61°) = 0.554309
ctg(62°) = 0.531709
ctg(63°) = 0.509525
ctg(64°) = 0.487733
ctg(65°) = 0.466308
ctg(66°) = 0.445229
ctg(67°) = 0.424475
ctg(68°) = 0.404026
ctg(69°) = 0.383864
ctg(70°) = 0.363970
ctg(71°) = 0.344328
ctg(72°) = 0.324920
ctg(73°) = 0.305731
ctg(74°) = 0.286745
ctg(75°) = 0.267949
ctg(76°) = 0.249328
ctg(77°) = 0.230868
ctg(78°) = 0.212557
ctg(79°) = 0.194380
ctg(80°) = 0.176327
ctg(81°) = 0.158384
ctg(82°) = 0.140541
ctg(83°) = 0.122785
ctg(84°) = 0.105104
ctg(85°) = 0.087489
ctg(86°) = 0.069927
ctg(87°) = 0.052408
ctg(88°) = 0.034921
ctg(89°) = 0.017455
ctg(90°) = 0

Таблица котангенсов углов от 91° до 180°

ctg(91°) = -0.017455
ctg(92°) = -0.034921
ctg(93°) = -0.052408
ctg(94°) = -0.069927
ctg(95°) = -0.087489
ctg(96°) = -0.105104
ctg(97°) = -0.122785
ctg(98°) = -0.140541
ctg(99°) = -0.158384
ctg(100°) = -0.176327
ctg(101°) = -0.194380
ctg(102°) = -0.212557
ctg(103°) = -0.230868
ctg(104°) = -0.249328
ctg(105°) = -0.267949
ctg(106°) = -0.286745
ctg(107°) = -0.305731
ctg(108°) = -0.324920
ctg(109°) = -0.344328
ctg(110°) = -0.363970
ctg(111°) = -0.383864
ctg(112°) = -0.404026
ctg(113°) = -0.424475
ctg(114°) = -0.445229
ctg(115°) = -0.466308
ctg(116°) = -0.487733
ctg(117°) = -0.509525
ctg(118°) = -0.531709
ctg(119°) = -0.554309
ctg(120°) = -0.577350

ctg(121°) = -0.600861
ctg(122°) = -0.624869
ctg(123°) = -0.649408
ctg(124°) = -0.674509
ctg(125°) = -0.700208
ctg(126°) = -0.726543
ctg(127°) = -0.753554
ctg(128°) = -0.781286
ctg(129°) = -0.809784
ctg(130°) = -0.839100
ctg(131°) = -0.869287
ctg(132°) = -0.900404
ctg(133°) = -0.932515
ctg(134°) = -0.965689
ctg(135°) = -1
ctg(136°) = -1.035530
ctg(137°) = -1.072369
ctg(138°) = -1.110613
ctg(139°) = -1.150368
ctg(140°) = -1.191754
ctg(141°) = -1.234897
ctg(142°) = -1.279942
ctg(143°) = -1.327045
ctg(144°) = -1.376382
ctg(145°) = -1.428148
ctg(146°) = -1.482561
ctg(147°) = -1.539865
ctg(148°) = -1.600335
ctg(149°) = -1.664279
ctg(150°) = -1.732051

ctg(151°) = -1.804048
ctg(152°) = -1.880726
ctg(153°) = -1.962611
ctg(154°) = -2.050304
ctg(155°) = -2.144507
ctg(156°) = -2.246037
ctg(157°) = -2.355852
ctg(158°) = -2.475087
ctg(159°) = -2.605089
ctg(160°) = -2.747477
ctg(161°) = -2.904211
ctg(162°) = -3.077684
ctg(163°) = -3.270853
ctg(164°) = -3.487414
ctg(165°) = -3.732051
ctg(166°) = -4.010781
ctg(167°) = -4.331476
ctg(168°) = -4.704630
ctg(169°) = -5.144554
ctg(170°) = -5.671282
ctg(171°) = -6.313752
ctg(172°) = -7.115370
ctg(173°) = -8.144346
ctg(174°) = -9.514364
ctg(175°) = -11.430052
ctg(176°) = -14.300666
ctg(177°) = -19.081137
ctg(178°) = -28.636253
ctg(179°) = -57.289962
ctg(180°) не определено

Синус острого угла прямоугольного треугольника

Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.

sin alpha = frac{a}{c}

Косинус острого угла прямоугольного треугольника

Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.

cos alpha = frac{b}{c}

Тангенс острого угла прямоугольного треугольника

Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.

tg alpha = frac{a}{b}

Котангенс острого угла прямоугольного треугольника

Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.

ctg alpha = frac{b}{a}

Синус произвольного угла

Ордината точки на единичной окружности, которой соответствует угол alpha называют синусом произвольного угла поворота alpha.

sin alpha=y

Косинус произвольного угла

Абсцисса точки на единичной окружности, которой соответствует угол alpha называют косинусом произвольного угла поворота alpha.

cos alpha=x

Тангенс произвольного угла

Отношение синуса произвольного угла поворота alpha к его косинусу называют тангенсом произвольного угла поворота alpha.
tg alpha = y_{A}
tg alpha = frac{sin alpha}{cos alpha}

Котангенс произвольного угла

Отношение косинуса произвольного угла поворота alpha к его синусу называют котангенсом произвольного угла поворота alpha.
ctg alpha =x_{A}
ctg alpha = frac{cos alpha}{sin alpha}

Пример нахождения произвольного угла

Если alpha — некоторый угол AOM, где M — точка единичной окружности, то
sin alpha=y_{M}, cos alpha=x_{M}, tg alpha=frac{y_{M}}{x_{M}}, ctg alpha=frac{x_{M}}{y_{M}}.
Например, если angle AOM = -frac{pi}{4}, то: ордината точки M равна -frac{sqrt{2}}{2}, абсцисса равна frac{sqrt{2}}{2} и потому
sin left (-frac{pi}{4}
ight )=-frac{sqrt{2}}{2};
cos left (frac{pi}{4}
ight )=frac{sqrt{2}}{2};
tg left (-frac{pi}{4}
ight )=-1;
ctg left (-frac{pi}{4}
ight )=-1.

Таблица значений синусов косинусов тангенсов котангенсов

Значения основных часто встречающихся углов приведены в таблице:

0^{circ} (0)	30^{circ}left(frac{pi}{6} ight)	45^{circ}left(frac{pi}{4} ight)	60^{circ}left(frac{pi}{3} ight)	90^{circ}left(frac{pi}{2} ight)	180^{circ}left(pi ight)	270^{circ}left(frac{3pi}{2} ight)	360^{circ}left(2pi ight)
sinalpha		frac12	frac{sqrt 2}{2}	frac{sqrt 3}{2}	1		−1
cosalpha	1	frac{sqrt 3}{2}	frac{sqrt 2}{2}	frac12		−1		1
tg alpha		frac{sqrt 3}{3}	1	sqrt3	—		—
ctg alpha	—	sqrt3	1	frac{sqrt 3}{3}		—		—

Основные способы, которые помогут заполнить таблицу функций

1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.

В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.

Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции

Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec)

2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение \ и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя \ можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.

Для наглядности все прописанные действия, можно разобрать на конкретном примере.

Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении \ записываем значение угла.

Получаем следующую запись: \. Затем, проводим те же операции для заполнения оставшихся пустых строк.

Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.

3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется 1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.

4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. \. Выходим что искомое значение равно данному выражению. Если \[\operatorname{tg} 45^{\circ}=\frac{\sin }{\cos }=\frac{\sqrt{1}}{2} / \frac{\sqrt{3}}{2}=\frac{1}{\sqrt{3}} .\]

Аналогично поступаем и далее.

5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.

Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.

Стандартные углы

Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.

Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:

Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.

Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.

3.1. Три стандартных угла

Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:

Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:

Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:

Это именно те значения, которые указаны в таблице!

Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:

Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.

Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:

Разберёмся с углом 60°:

И с углом 30°:

Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!

Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.

Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?

3.2. Что с другими углами?

Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:

Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:

Итак, мы знаем синус

Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$

Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует

Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.

Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:

Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.

Ещё раз:

И наоборот:

С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.

Что такое таблицы тригонометрических функций

Определение

Тригонометрические функции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе.

Для определения неизвестных элементов треугольника (сторон или углов), необходимо использовать известные элементы и правила зависимости между ними. Подобные зависимости называют также тригонометрическими функциями. Таким образом, зная значения некоторого угла или стороны, пользуясь тригонометрическими функциями можно найти неизвестные углы и стороны треугольника. Именно поэтому, без знаний тригонометрии решать геометрические задачи не представляется возможным.

Основные тригонометрические функции:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Синус — отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему. Также равен частному от деления синуса определенного угла на его косинус.
Котангенс — отношение прилежащего катета к противолежащему. Также равен частному от деления косинуса определенного угла на его синус.

Примечание

Синус и косинус являются прямыми тригонометрическими функциями, тангенс и котангенс — производными. Существуют и другие тригонометрические функции, например — арктангенс. Арктангенс относится к так называемым обратным тригонометрическим функциям, и является функцией, обратной тангенсу. Это означает, что если тангенс некоторого угла у градусов (радиан) равен х, значит арктангенс x равняется y градусов (радиан).

Вычисленные тригонометрические функции (синус, косинус и тангенс) представляют в виде специальных таблиц, которые можно использовать при решении задач — это и есть таблицы тригонометрических функций. В них приведены значения тригонометрических функций углов от 0° до 360°.

Для прямоугольных треугольников в диапазоне углов от 30° до 90° тригонометрические функции равняются следующим значениям:

sin 30° = 1/2, cos 30° = √3/2, tg 30° = √3/3, ctg 30° = √3
sin 45° = √2/2, cos 45° = √2/2, tg 45°= 1, ctg 45° = 1
sin 60° = √3/2, cos 60° = 1/2, tg 60° =√3 , ctg 60° = √3/3

Как выглядит для значений, синуса, косинуса, тангенса и котангенса

Таблица тригонометрических функций выглядит следующим образом:

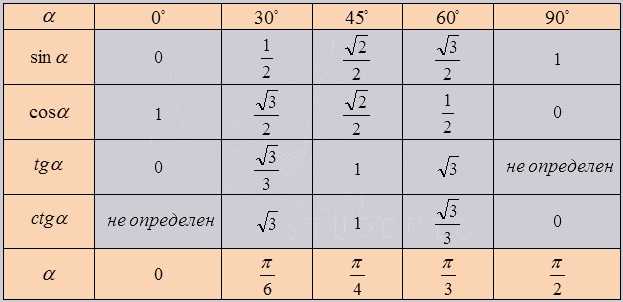
Значение аргумента α задано в верхней строке задано в градусах (от 0° до 90°), во второй строке — в радианах (0, π/6, π/4, π/3, π/2 радиан). Иногда в таблице присутствуют значения только в радианах. Для перевода в градусы необходимо подставить число π = 180°, например, π/6 = 180/6 = 30°.

Обозначение «не определен» в таблице (тангенс 90° и котангенс 0°) означает, что функция является неопределенной.

Пример

Алгоритм решения задач с помощью данной таблицы крайне прост. К примеру, нам необходимо найти значение косинуса 30°. Для этого найдем ячейку пересечения строки косинуса и столбца значений для 30°. В данной ячейке находится искомое значение.

Свойства тригонометрических функций[править | править код]

Функция y = cos α — чётная, функции: y = sin α, y = tg α, y = ctg α — нечётные, то есть:
sin Синус (−α)=−sin Синус α, \sin \left( — \alpha \right) = — \sin \alpha\,,cos Косинус (−α)=cos Косинус α, \cos \left( — \alpha \right) = \cos \alpha\,,tg(−α)=−tgα, \mathop{\mathrm{tg}}\, \left( — \alpha \right) = — \mathop{\mathrm{tg}}\, \alpha\,,ctg(−α)=−ctgα. \mathop{\mathrm{ctg}}\, \left( — \alpha \right) = — \mathop{\mathrm{ctg}}\, \alpha\,.

Для острых углов α<π2 \alpha < \frac{ \pi}{2}\,\!
справедливо:
sin Синус (π2−α)=cos Косинус α, \sin \left( \frac{ \pi}{2} — \alpha \right) = \cos \alpha\,,cos Косинус (π2−α)=sin Синус α, \cos \left( \frac{ \pi}{2} — \alpha \right) = \sin \alpha\,,tg(π2−α)=ctgα, \mathop{\mathrm{tg}}\, \left( \frac{ \pi}{2} — \alpha \right) = \mathop{\mathrm{ctg}}\, \alpha\,,ctg(π2−α)=tgα. \mathop{\mathrm{ctg}}\, \left( \frac{ \pi}{2} — \alpha \right) = \mathop{\mathrm{tg}}\, \alpha\,.

Для углов <α<π 0 < \alpha < \pi \,\! справедливо:
sin Синус (π−α)=sin Синус α, \sin \left( \pi — \alpha \right) = \sin \alpha\,,cos Косинус (π−α)=−cos Косинус α, \cos \left( \pi — \alpha \right) = — \cos \alpha\,,tg(π−α)=−tgα,α≠π2. \mathop{\mathrm{tg}}\, \left( \pi — \alpha \right) = — \mathop{\mathrm{tg}}\, \alpha, \qquad \alpha \ne \frac{ \pi}{2}\,.

Рассмотрим треугольник ABO (см. Рис. 1). По теореме Пифагора:
(AB)2+(BO)2=(OA)2, \left(AB \right)^2 + \left(BO \right)^2 = \left(OA \right)^2 \,,
если OA = 1, то AB = sin α и OB = cos α, то есть
sin Синус 2α+cos Косинус 2α=1.(1) \sin^2 \alpha + \cos^2 \alpha = 1. \qquad \qquad (1)\,

Если разделить выражение (1) на cos Косинус 2α, \cos^2 \alpha \,, то получим следующее тождество:
1+tg2α=1cos Косинус 2α.(2) 1 + \mathop{\mathrm{tg}}\,^2 \alpha = \frac{1}{ \cos^2 \alpha}. \qquad \qquad (2) \,

Если разделить выражение (1) на sin Синус 2α, \sin^2 \alpha \,, то получим следующее тождество:
1+1tg2α=1sin Синус 2α,(3) 1 + \frac{1}{ \mathop{\mathrm{tg}}\,^2 \alpha} = \frac{1}{ \sin^2 \alpha}, \qquad \qquad (3) \,
или
1+ctg2α=1sin Синус 2α.(4) 1 + \mathop{\mathrm{ctg}}\,^2 \alpha = \frac{1}{ \sin^2 \alpha}. \qquad \qquad (4) \,

Вычисление данных при помощи фигуры — прямоугольный треугольник

Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.

Вычисление при помощи длин сторон треугольника происходит следующим образом:

обозначается катет;
сторона возле угла;
сторона напротив угла с прямым значением.

Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin\

Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.

В процессе решения задачи, это придется применять постоянно.

Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.

Косеканс находится \ следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету \.

Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.

При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.

Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.

Свойства тангенсоиды и котангенсоиды

Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.

Основные свойства котангенсоиды:

Y = tg x.
В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
Наименьший положительный период тангенсоиды равен π.
Tg (- x) = — tg x, т. е. функция нечетная.
Tg x = 0, при x = πk.
Функция является возрастающей.
Tg x › 0, при x ϵ (πk, π/2 + πk).
Tg x ‹ 0, при x ϵ ( — π/2 + πk, πk).
Производная (tg x)’ = 1/cos2⁡x .

Рассмотрим графическое изображение котангенсоиды ниже по тексту.

Основные свойства котангенсоиды:

Y = ctg x.
В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
Наименьший положительный период котангенсоиды равен π.
Ctg (- x) = — ctg x, т. е. функция нечетная.
Ctg x = 0, при x = π/2 + πk.
Функция является убывающей.
Ctg x › 0, при x ϵ (πk, π/2 + πk).
Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
Производная (ctg x)’ = — 1/sin2⁡x Исправить

Тригонометрические функции в прямоугольном треугольнике[]

Чтобы определить тригонометрические функции произвольного угла α,{\displaystyle \alpha ,} возьмём произвольный прямоугольный треугольник, содержащий угол α{\displaystyle \alpha }. Стороны этого треугольника мы будем называть так:

Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c.{\displaystyle c.}
Противолежащий катет — катет, лежащий напротив угла. Например, катет a{\displaystyle a} — противолежащий по отношению к углу A.{\displaystyle A.}
Прилежащий катет — катет, являющийся стороной угла. Например, катет b{\displaystyle b} — прилежащий по отношению к углу A.{\displaystyle A.}

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π.{\displaystyle \pi .} Это означает, что углы между катетами и гипотенузой лежат между {\displaystyle 0} и π2.{\displaystyle {\frac {\pi }{2}}.} Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Си́нус угла — отношение противолежащего катета к гипотенузе: sin⁡α=ac.{\displaystyle \sin \alpha ={\frac {a}{c}}.} Это отношение не зависит от выбора треугольника ABC{\displaystyle {ABC}}, содержащего угол α,{\displaystyle \alpha ,} так как все такие треугольники подобны.

Ко́синус угла — отношение прилежащего катета к гипотенузе: cos⁡α=bc.{\displaystyle \cos \alpha ={\frac {b}{c}}.} Так как sin⁡β=bc,{\displaystyle \sin \beta ={\frac {b}{c}},} синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Та́нгенс угла — отношение противолежащего катета к прилежащему: tgα=ab.{\displaystyle \operatorname {tg} \,\alpha ={\frac {a}{b}}.}

Кота́нгенс угла — отношение прилежащего катета к противолежащему: ctgα=ba.{\displaystyle \operatorname {ctg} \,\alpha ={\frac {b}{a}}.} Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Се́канс угла — отношение гипотенузы к прилежащему катету: sec⁡α=cb.{\displaystyle \sec \alpha ={\frac {c}{b}}.}

Косе́канс угла — отношение гипотенузы к противолежащему катету: cosecα=ca.{\displaystyle \operatorname {cosec} \,\alpha ={\frac {c}{a}}.}

Из определений тригонометрических функций следует:

a=csin⁡α,{\displaystyle a=c\sin \alpha \,,}

b=ccos⁡α,{\displaystyle b=c\cos \alpha \,,}

a=btgα,{\displaystyle a=b\,\operatorname {tg} \,\alpha ,}

b=actgα,{\displaystyle b=a\,\operatorname {ctg} \,\alpha ,}

c=bsec⁡α,{\displaystyle c=b\sec \alpha \,,}

c=acosecα,{\displaystyle c=a\,\operatorname {cosec} \,\alpha ,}

и симметрично:

b=csin⁡β,{\displaystyle b=c\sin \beta \,,}

a=ccos⁡β,{\displaystyle a=c\cos \beta \,,}

b=atgβ,{\displaystyle b=a\,\operatorname {tg} \,\beta ,}

a=bctgβ,{\displaystyle a=b\,\operatorname {ctg} \,\beta ,}

c=asec⁡β,{\displaystyle c=a\sec \beta \,,}

c=bcosecβ.{\displaystyle c=b\,\operatorname {cosec} \,\beta .}

Основные величины тригонометрии

Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.

В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.

Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:

Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:

Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике

Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?

Давай разбираться. Для этого нам поможет прямоугольный треугольник.

Как называются стороны прямоугольного треугольника?

Всё верно, гипотенуза и катеты.

Причём, если рассматривать катеты относительно угла $ \angle BAC$, то катет $ AB$ – это прилежащий катет, а катет $ BC$ — противолежащий.

Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?

В нашем треугольнике $ \sin \beta =\frac{BC}{AC}$.

В нашем треугольнике $ \cos \beta =\frac{AB}{AC}$.

В нашем треугольнике $ tg\beta =\frac{BC}{AB}$.

В нашем треугольнике $ ctg\beta =\frac{AB}{BC}$.

Эти определения необходимо запомнить!

А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:

Косинус→касаться→прикоснуться→прилежащий;

Котангенс→касаться→прикоснуться→прилежащий.

В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).

Не веришь?

Тогда убедись, посмотрев на рисунок:

Рассмотрим, к примеру, косинус угла $ \beta $.

По определению, из треугольника $ ABC$: $ \cos \beta =\frac{AB}{AC}=\frac{4}{6}=\frac{2}{3}$.

Но ведь мы можем вычислить косинус угла $ \beta $ и из треугольника $ AHI$: $ \cos \beta =\frac{AH}{AI}=\frac{6}{9}=\frac{2}{3}$.

Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.

Если разобрался в определениях, то вперёд закреплять их!

Для треугольника $ ABC$, изображённого ниже на рисунке, найдём $ \sin \ \alpha ,\ \cos \ \alpha ,\ tg\ \alpha ,\ ctg\ \alpha $.

$ \begin{array}{l}\sin \ \alpha =\frac{4}{5}=0,8\\\cos \ \alpha =\frac{3}{5}=0,6\\tg\ \alpha =\frac{4}{3}\\ctg\ \alpha =\frac{3}{4}=0,75\end{array}$Ну что, уловил?

Тогда пробуй сам: посчитай то же самое для угла $ \beta $.