Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса

Решение

Для решения этого уравнения удобно разместить один тип тригонометрической функции, поэтому мы будем использовать фундаментальное тригонометрическое тождество, чтобы исходное уравнение было переписано следующим образом:

соз (х) = 1 — соз2(Икс)

Если мы назовем y = cos (x), выражение можно переписать как:

Y2 + и — 1 = 0

Это уравнение второй степени по y, решениями которого являются:

у = (-1 ± √5) / 2

Тогда значения x, которые удовлетворяют исходному уравнению, следующие:

х = arccos ((-1 ± √5) / 2)

Реальным решением является решение с положительным знаком x = 0,9046 рад = 51,83º.

Другое решение комплексное: x = (π — 1,06 i) рад.

Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса

1. Исходим из t g α = sin α 1 — sin 2 α , — π 2 α π 2 . Получаем t g ( a r c sin α ) = sin ( a r c sin α ) 1 — sin 2 ( a r c sin α ) = α 1 — α 2 при условии, что — 1 α 1 .
2. Исходим из t g α = 1 — cos 2 α cos α , α ∈ , получаем

t g ( a r c cos α ) = 1 — cos 2 ( a r c cos α ) cos ( a r c c os α ) = 1 — α 2 α при условии α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) .

1. Исходим из t g α = 1 c t g α , α ∈ ( 0 , π 2 ) ∪ ( π 2 , π ) , получаем t g ( a r c c t g α ) = 1 c t g ( a r c c t g α ) = 1 α при условии, что α ≠ 0 .

Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:

c t g α = 1 t g α

Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.

Примеры решения задач

Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

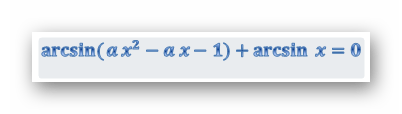
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.

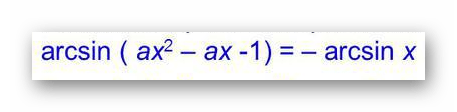
Если вспомнить формулу arcsin (sin α) = α
, то можно свести поиск ответов к решению системы из двух уравнений:

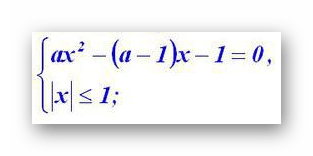
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x . При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.

Как найти арксинус: формула, свойства, функция

Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).

Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу. В результате с помощью синуса можно, учитывая дугу окружности, определить хорду, которая ее стягивает.

Обратная функция под названием арксинус призвана решить противоположную задачу. Арксинус обозначают \(\arcsin x\) и определяют, как угол с синусом, равным х.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Для тригонометрических функций характерна периодичность. В связи с этим, обратные тригонометрические функции являются многозначными. Аркфункция обладает значением в виде множества из углов, для которых прямая тригонометрическая функция соответствует заданному числу.

Рассмотрим функцию: \(\arcsin ½\) . Данная аркфункция обозначает множество из углов:

(30^\circ, 150^\circ, 390^\circ, 510^\circ \dots) \right )\)

Значение синуса при этом: ½

Как правило, под обратными тригонометрическими функциями понимают ключевые значения каждой аркфункции, выделенные из ее множества значений.

Если \(-1\leqslant \alpha \leqslant 1\) , то любое решение уравнения \(\sin x=\alpha\) записывают в такой форме: \( x=(-1)^\arcsin \alpha +\pi n,

Арксинус числа х — значение для угла у, определенного в радианах, для которого \(\sin y=x,\quad —>\leqslant y\leqslant >,\quad |x|\leqslant 1\) .

Зачем нужен арксинус

С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.

В том случае, когда имеется некий прямоугольный треугольник, обратные тригонометрические функции от отношений сторон позволяют определить угол. Например, длина катета составляет «а». Этот катет определяется, как противолежащий для угла \(\alpha\) , то:

\(\alpha =\arcsin(a/c)=\arccos(b/c)=\operatorname (a/b)=\operatorname (c/a)=\operatorname (c/b)=\operatorname (b/a)\)

Получение функции arcsin с пояснением на примерах

Предположим, что существует некая функция:

Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=\arcsin x нельзя причислить к функциям.

В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:

Функция \(y=\sin x \) на отрезке \(\left\) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой \(y=\arcsin x.\)

График обратной функции является симметричным графику функции \(y=\sin x\) в рамках интервала \(\left\) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.

Определим значение выражение:

По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.

Требуется найти, что означает \(\arcsin 0,5\) .

Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:

Общий ответ можно высчитать не в градусах, а в радианах:

Свойства функции arcsin

Рассмотрим функцию \(y=\arcsin x\) . Она является непрерывной в тригонометрии и ограничивается на протяжении всей своей области определения. Данная функция строго возрастает.

Определения тригонометрических функций

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1.

Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от .

=  

=  

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0; 1) и (0; -1). В таких случаях выражение для тангенса просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом.  Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Синус и косинус определены для любых углов .

При решении практических примеров не говорят «синус угла поворота «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом числа называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в радиан.

Например, синус числа равен синусу угла поворота величиной рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами (1;0).

Положительному числу  соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь длиной .

Отрицательному числу соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь длиной ||.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу , совпадает с точкой, в которую переходит начальная точка после поворота на угол радиан.

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.

Взгляните:

Синим цветом обозначено положительное направление оси (ось ординат), красным — положительное направление оси (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными.

В частности,

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

Знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Таблица значений синусов, косинусов, тангенсов и котангенсов для основных углов.

Синус от арккосинуса, тангенс от арксинуса и иже с ними

На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.

Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид , таким образом .

Другой пример: используя формулу синуса арккосинуса вида , мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем . Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).

Осталось показать вывод записанных формул.

Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.

Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств и , а также учитывая, что , легко получить следующие формулы , и , выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.

Вот краткая запись вышеперечисленных выкладок:

• так как , то ;
• так как , то ;
• так как , то .

По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:

• так как , то ;
• так как , то ;
• так как , то .

Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:

• так как , то при ;
• так как , то при ;
• так как , то при .

Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как .

Арксинус и арккосинус − теория, примеры и решения

Функция арксинус и ее график

Как известно, функция синус определена в интервале и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t₁=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t₂=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

При a=−1, имеем cos t=−1,

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:

Решение уравнения cosx = a

Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:

По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь

Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:

Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:

Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:

Здесь мы использовали тот факт, косинус – четная функция, то есть

Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:

Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть

Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:

Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение

При n = 5 получим корень

При n = – 10 у нас получится решение

Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:

Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень

Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:

Объединить же обе серии можно одной записью:

Напомним, что мы решали ур-ние

и получили для него решение

Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид

где а – некоторое число, его решением будут все такие х, что

Для краткости запись «n– целое число» заменяют эквивалентной записью

«n ∈ Z»

Напомним, что буквой Z обозначают множество целых чисел.

Задание. Решите ур-ние

Решение. Вспомним, что

Задание. Решите ур-ние

Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:

Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.

Задание. Укажите три наименьших положительных корня ур-ния

Решение. Так как

то все решения образуют две серии:

Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.

Для первой серии:

Для второй серии:

Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):

Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4

Ответ: π/4, 7π/4 и 9π/4.

Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния

На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния

являются точки, в которых график пересекает ось Ох:

Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок .

Вынесение общего множителя в тригонометрических уравнениях

Еще один распространенный на ЕГЭ тип тригонометрических уравнений, в которых необходимо вынести общий множитель.

Пример 27
$$\sin(2x)-2\sin^2(x)=0;$$

В этом уравнении только одна тригонометрическая функция — \(\sin(x)\). Но под синусами стоят разные выражения. Поэтому избавимся от двойного угла под синусом при помощи формулы синуса двойного угла:
$$\sin(2x)=2\sin(x)*\cos(x);$$
Уравнение примет вид:
$$2\sin(x)*\cos(x)-2\sin^2(x)=0;$$
Замечаем общий множитель \(2*\sin(x)\), вынесем его за скобки:
$$2*\sin(x)*(\cos(x)-\sin(x))=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Уравнение разбивается на два:
Либо:
$$2\sin(x)=0;$$
$$\sin(x)=0;$$
$$x_{1}=0+2\pi*n=2\pi*n, \quad n \in Z;$$
$$x_{2}=\pi+2\pi*n, \quad n \in Z;$$
(Кстати, эти два решения можно объединить в одно: \(x=0+\pi*n=\pi*n, \quad n \in Z;\))
Либо второе уравнение:
$$\cos(x)-\sin(x)=0;$$
Это уравнение решается при помощи деления. Разделим левую и правую часть уравнения на \(\cos(x)\):
$$\frac{\cos(x)-\sin(x)}{\cos(x)}=\frac{0}{\cos(x)};$$
$$1-\frac{sin(x)}{\cos(x)}=0;$$
$$1-tg(x)=0;$$
$$tg(x)=1;$$
$$x=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$

Ответ:
$$x_{1}=\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{4}+\pi*n, \quad n \in Z;$$

Пример 28
$$2\cos(\frac{\pi}{2}-x)=tg(x);$$

Сразу замечаем формулу приведения под косинусом:
$$\cos(\frac{\pi}{2}-x)=\sin(x);$$
Подставляем в исходное уравнение
$$2\sin(x)=tg(x);$$
Распишем тангенс по определению:
$$tg(x)=\frac{\sin(x)}{\cos(x)};$$
$$2\sin(x)=\frac{\sin(x)}{\cos(x)};$$
$$2\sin(x)-\frac{\sin(x)}{\cos(x)}=0;$$
И здесь тоже будет общий множитель \(\sin(x)\):
$$\sin(x)*(2-\frac{1}{\cos(x)})=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
Первый множитель:
$$\sin(x)=0;$$
$$x_{1}=0+\pi*n=\pi*n, \quad n \in Z;$$
Второй множитель:
$$2-\frac{1}{\cos(x)}=0;$$
Приведем к общему знаменателю:
$$\frac{2\cos(x)}{\cos(x)}-\frac{1}{\cos(x)}=0;$$
$$\frac{2\cos(x)-1}{\cos(x)}=0;$$
Дробь равна нулю, когда числитель равен нулю – избавляемся от знаменателя:
$$2\cos(x)-1=0;$$
$$2\cos(x)=1;$$
$$\cos(x)=\frac{1}{2};$$
$$x_{2}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$x_{3}=-\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$

Ответ:
$$x_{1}=\pi*n, \quad n \in Z;$$
$$x_{2}=\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$
$$x_{3}=-\frac{\pi}{3}+2\pi*n, \quad n \in Z;$$

Метод группировки в тригонометрических уравнениях

Рассмотрим еще уравнение, которое было на ЕГЭ 2015 года на метод группировки. Тоже нужно обязательно это знать. Сам метод, если кто не знает, сводится, по сути, к вынесению общего множителя за скобки, только немного сложнее.

Пример 29
$$\sin(2x)+\sqrt{2}\sin(x)=2\cos(x)+\sqrt{2};$$

Избавляемся от двойного угла:
$$2*\sin(x)\cos(x)+\sqrt{2}\sin(x)=2\cos(x)+\sqrt{2};$$
И перенесем все в левую часть:
$$2*\sin(x)\cos(x)+\sqrt{2}\sin(x)-2\cos(x)-\sqrt{2}=0;$$
У нас 4 слагаемых, сгруппируем их попарно: 1-е со 2-м, а 3-е с 4-м, и вынесем в каждой паре общий множитель:
$$\sin(x)(2\cos(x)+\sqrt{2})-1(2\cos(x)+\sqrt{2})=0;$$
У 3-го и 4-го слагаемых я вынес за скобки \(-1\).

Теперь обратите внимание, что в скобках получились идентичные выражения, то есть эти скобки абсолютно одинаковые. Вынесем эту общую скобку за скобку!
$$(2\cos(x)+\sqrt{2})(\sin(x)-1)=0;$$
Вот мы и сгруппировали, теперь приравниваем каждый множитель к нулю:
Первый множитель:
$$2\cos(x)+\sqrt{2}=0;$$
$$\cos(x)=\frac{-\sqrt{2}}{2};$$
$$x_{1}=\frac{3\pi}{4}+2\pi*n, \quad n \in Z;$$
$$x_{2}=-\frac{3\pi}{4}+2\pi*n, \quad n \in Z;$$
Второй множитель:
$$\sin(x)-1=0;$$
$$\sin(x)=1;$$
$$x_{3}=\frac{\pi}{2}+2\pi*n, \quad n \in Z;$$

Арктангенс, арккотангенс – свойства, графики, формулы

График функции y = arctg x .

График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.

Арккотангенс, arcctg

График функции арккотангенс

График функции y = arcctg x .

График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.

Четность

Функция арктангенс является нечетной: arctg(– x ) = arctg(–tg arctg x ) = arctg(tg(–arctg x )) = – arctg x

Функция арккотангенс не является четной или нечетной: arcctg(– x ) = arcctg(–ctg arcctg x ) = arcctg(ctg(π–arcctg x )) = π – arcctg x ≠ ± arcctg x .

Свойства – экстремумы, возрастание, убывание

Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.

y = arctg x	y = arcctg x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Множество значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы, минимумы	нет	нет
Нули, y = 0	x = 0	нет
Точки пересечения с осью ординат, x = 0	y = 0	y = π/ 2
–	π

В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.