Таблица тангенсов и котангенсов: 0 - 360 градусов, как пользоваться

Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов

Список литературы.

Алгебра:
Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Башмаков М. И.
Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра
и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Гусев В. А., Мордкович А. Г.
Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Брадис В. М.
Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2

Главные значения: arcsin, arccos, arctg и arctg

Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \ градусов. Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.

Продолжение таблицы 1

Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.

Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.

Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.

Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.

И напоследок остается вычислить значения арктангенса и арккотангенса.

Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:

\ — данные угловые значения, не определяются, согласно основным законам геометрии и математики.

\- для перечисленных угловых значений по законам математики и всех технических наук в целом, значения не определяются

Далее все данные запишем в виде табличной формы.

Первая таблица для арктангенса

Вторая таблица для арккотангенса

Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.

Например:

Основные способы, которые помогут заполнить таблицу функций тригонометрии.

Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.

В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.

Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции

Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec)

На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения.

Дважды разделить, умножить и отнять.

Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.

В таблице представлены следующие данные:

число в квадратной и кубической степени;
числа квадратных корней;
логарифмические функции и значение;
функции тригонометрии, представленный в градусах и радианах;
обратные функции.

Мы показали, что представляет таблица, какие данные и значения отображает. Полную версию таблицы, можно найти в сборнике. Который издается каждый год. Для определения неизвестных нужно использовать следующие уже известные нам формулы:

Пример решения:

Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102

Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение. Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.

Арксинус (y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).

Свойства функции	Функции y=arcsin х
E(f)	\
D(f)	\
наличие четности	Нечётная, т.к. arcsin(-x)= — arcsin x
характер графика направление	возрастание

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y).

Свойства	Функции y=arccos х
E(f)	\
D(f)	\
Чётности	Данное свойство ей не характерно. Иными словами отсутствует.
Монотонность	Убывающая

Арктангенс ( y = arctg x ) – характеризуется, как обратное значение функции относительно тангенса.

Следовательно арккотангенс имеет такие свойства по отношению к тангенсу.

Свойства	y=arctg х	y=arcctg х
E(f)	R	R
D(f)	\	\
Характер функции	Нечётная	Нечётная
Периоды	Возрастающая	Убывающая

Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, …, 360 градусов

Исходя из определений синуса, косинуса, тангенса и котангенса можно найти значения этих функций для углов 0 и 90 градусов

sin 0=0, cos 0=1, tg 0=0, котангенс нуля – не определен,

sin 90°=1, cos 90°=0, сtg 90°=0, тангенс дявяноста градусов не определен.

Значения синусов, косинусов, тангенсов и котангенсов в курсе геометрии определяются как соотношения сторон прямоугольного треугольника, углы которого равны 30, 60 и 90 градусов, и также 45, 45 и 90 градусов.

Определение тригонометрических функуций для острого угла в прямоугольном треугольнике

Синус – отношение противолежащего катета к гипотенузе.

Косинус – отношение прилежащего катета к гипотенузе.

Тангенс – отношение противолежащего катета к прилежащему.

Котангенс – отношение прилежащего катета к противолежащему.

В соответствии с определениями находятся значения функций:

sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3,sin 45°=22, cos 45°=22, tg 45°=1, ctg 45°=1,sin 60°=32, cos 45°=12, tg 45°=3, ctg 45°=33.

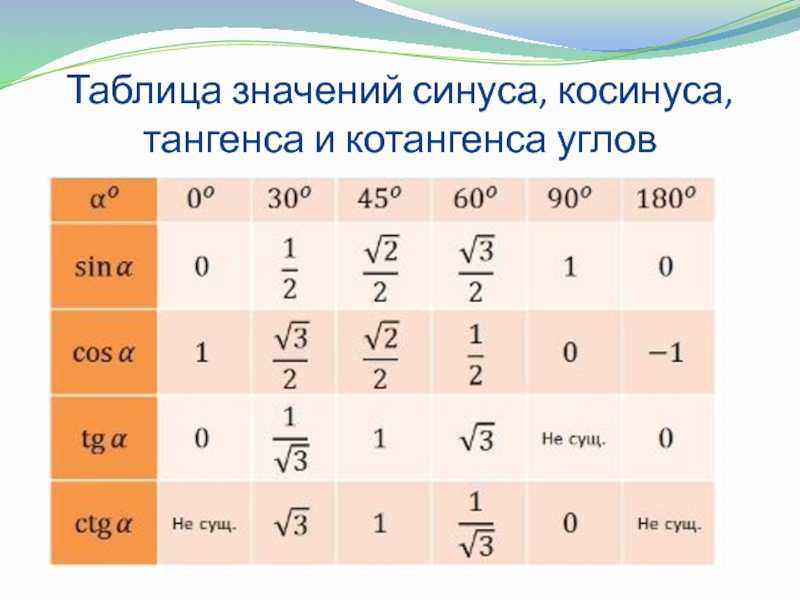
Сведем эти значения в таблицу и назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.

Таблица основных значений синусов, косинусов, тангенсов и котангенсов

α°030456090sin α01222321cos α13222120tg α03313не определенctg αне определен31330α, радиан0π6π4π3π2

Одно из важных свойств тригонометрических функций – периодичность. На основе этого свойства данную таблицу можно расширить,используя формулы приведения. Ниже представим расширенную таблицу значений основных тригонометрических функций для углов 0, 30, 60, … ,120, 135, 150, 180, … , 360 градусов ( 0 , π 6 , π 3 , π 2 , . . . , 2 π радиан).

Таблица синусов, косинусов, тангенсов и котангенсов

α°030456090120135150180210225240270300315330360sin α012223213222120-12-22-32-1-32-22-120cos α13222120-12-22-32-1-32-22-1201222321tg α03313–1-33003313–3-1 0ctg α-31330-33-1-3-31330-33-1-3-α, радиан0π6π4π3π22π33π45π6π7π65π44π33π25π37π411π62π

Периодичность синуса, косинуса, тангенса и котангенса позволяет расширять эту таблицу до сколь угодно больших значений углов. Значения, собранные в таблице, используются при решении задач чаще всего, поэтому их рекомендуется выучить наизусть.

Тригонометрия и тригонометрические функции

Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.

Функция – это правило, описывающее зависимость одной величины от другой.

Угол – это геометрическая фигура, образованная двумя линиями, не лежащими на одной прямой и выходящими или пересекающимися в одной точке.

Углы по своему виду могут быть:

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

В зависимости от соотношения сторон и углов, треугольники можно разделить на группы:

По величине угла:
прямоугольный
тупоугольный
остроугольный

По длине сторон:
равносторонний
разносторонний
равнобедренный

Таблица котангенсов углов от 0° — 360°. Углы с шагом в 1°. Вариант для печати.

Углы
1° — 90° Углы
91 ° — 180° Углы
181° — 270° Углы
271 ° — 360° Угол Ctg Угол Ctg Угол Ctg Угол Ctg

Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций

Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов. Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов. Таблица синусов, она-же косинусов точная. Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg Таблица тангенсов, она же котангенсов точная. Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π).
Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге. Определение и численные соотношения между единицами измерения углов в РФ.
Тысячные, угловые градусы, минуты, секунды, радианы, обороты. Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите, пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Консультации и техническая
Поддержка сайта: Zavarka Team

Таблица котангенсов — это записанные в таблицу посчитанные значения котангенсов углов от 0° до 360°. Используя таблицу котангенсов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение котангенса от нужного Вам угла, достаточно найти его в таблице или вычислить с помощью калькулятора.

Таблица котангенсов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg

Углы
1° — 90° Углы
91 ° — 180° Углы
181° — 270° Углы
271 ° — 360° Угол Ctg Угол Ctg Угол Ctg Угол Ctg

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Консультации и техническая
Поддержка сайта: Zavarka Team

В таблице значения котангенсов от 0° до 360°. Таблица котангенсов нужна, когда у вас под рукой нет калькулятора, чтобы узнать, чему равен котангенс угла. Короткая версия таблицы:

Таблица котангенсов для 0°-180°

36397 ctg 291 -0.

02.05.2020 22:06:23

2020-05-02 22:06:23

Любые данныеЛюбые данныеЛюбые данныеЛюбые данные Любые данные

Таблица Брадиса для тангенса и котангенса

Таблицей Брадиса представляет собой таблицу, с помощью которой можно производить различные практические вычисления, не требующие повышенной точности, а также работы по математике, в том числе рассчитать тригонометрические величины.

Примечание

Табличная форма полезна при решении задач разной степени сложности по математике, алгебре, геометрии и физике — помимо прямых и обратных тригонометрических функций она содержит значения логарифмов, квадратных корней, кубов и квадратов чисел. Также она необходима для поиска ответов на примеры из вузовских учебных программ.

Владимир Модестович Брадис (1890 – 1975) был советским математиком-педагогом, а с 1954 года являлся членом-корреспондентом АПН СССР. Брадис разработал таблицы четырехзначных логарифмов и натуральных тригонометрических величин, которые были опубликованы впервые в 1921 году.

Таблица состоит из двух частей. Первая структура содержит тангенсы от 0 до 75 градусов и котангенсы от 15 до 90 градусов. Они определены по средствам специальных столбцов для 1, 2 и 3 минут. Вторая часть включает тангенсы от 75 до 90 градусов и котангенсы от 0 до 15 градусов, точность записи которых соответствует 1 минуте угла. Таблица Брадиса:

Таблицы для всех углов

Если в таблицах выше показаны только тригонометрические значения особых углов, то в этой таблице показаны все тригонометрические значения всех углов от 0 до 90 градусов.

Угловой	Радианы	Грех	Cos	Загар
0 °	1
1 °	0,01746	0,01746	0,99985	0,01746
2 °	0,03492	0,03491	0,99939	0,03494
3 °	0,05238	0,05236	0,99863	0,05243
4 °	0,06984	0,06979	0,99756	0,06996
5 °	0,0873	0,08719	0,99619	0,08752
6 °	0,10476	0,10457	0,99452	0,10515
7 °	0,12222	0,12192	0,99254	0,12283
8 °	0,13968	0,13923	0,99026	0,1406
9 °	0,15714	0,1565	0,98768	0,15845
10 °	0,1746	0,17372	0,9848	0,1764
11 °	0,19206	0,19089	0,98161	0,19446
12 °	0,20952	0,20799	0,97813	0,21265
13 °	0,22698	0,22504	0,97435	0,23096
14 °	0,24444	0,24202	0,97027	0,24943
15 °	0,26191	0,25892	0,9659	0,26806
16 °	0,27937	0,27575	0,96123	0,28687
17 °	0,29683	0,29249	0,95627	0,30586
18 °	0,31429	0,30914	0,95102	0,32506
19 °	0,33175	0,32569	0,94548	0,34448
20 °	0,34921	0,34215	0,93965	0,36413
21 °	0,36667	0,35851	0,93353	0,38403
22 °	0,38413	0,37475	0,92713	0,40421
23 °	0,40159	0,39088	0,92044	0,42467
24 °	0,41905	0,40689	0,91348	0,44543
25 °	0,43651	0,42278	0,90623	0,46652
26 °	0,45397	0,43854	0,89871	0,48796
27 °	0,47143	0,45416	0,89092	0,50976
28 °	0,48889	0,46965	0,88286	0,53196
29 °	0,50635	0,48499	0,87452	0,55458
30 °	0,52381	0,50018	0,86592	0,57763
31 °	0,54127	0,51523	0,85706	0,60116
32 °	0,55873	0,53011	0,84793	0,62518
33 °	0,57619	0,54483	0,83854	0,64974
34 °	0,59365	0,55939	0,8289	0,67486
35 °	0,61111	0,57378	0,81901	0,70057
36 °	0,62857	0,58799	0,80887	0,72693
37 °	0,64603	0,60202	0,79848	0,75396
38 °	0,66349	0,61587	0,78785	0,78172
39 °	0,68095	0,62953	0,77697	0,81024
40 °	0,69841	0,643	0,76586	0,83958
41 °	0,71587	0,65628	0,75452	0,86979
42 °	0,73333	0,66935	0,74295	0,90094
43 °	0,75079	0,68222	0,73115	0,93308
44 °	0,76825	0,69488	0,71913	0,96629
45 °	0,78571	0,70733	0,70688	1 00063
46 °	0,80318	0,71956	0,69443	1,0362
47 °	0,82064	0,73158	0,68176	1,07308
48 °	0,8381	0,74337	0,66888	1,11137
49 °	0,85556	0,75494	0,6558	1,15117
50 °	0,87302	0,76627	0,64252	1,1926
51 °	0,89048	0,77737	0,62904	1,2358
52 °	0,90794	0,78824	0,61537	1,28091
53 °	0,9254	0,79886	0,60152	1,32807
54 °	0,94286	0,80924	0,58748	1,37748
55 °	0,96032	0,81937	0,57326	1.42932
56 °	0,97778	0,82926	0,55887	1,48382
57 °	0,99524	0,83889	0,5443	1,54122
58 °	1,0127	0,84826	0,52957	1,60179
59 °	1.03016	0,85738	0,51468	1,66584
60 °	1,04762	0,86624	0,49964	1,73374
61 °	1,06508	0,87483	0,48444	1,80587
62 °	1,08254	0,88315	0,46909	1,8827
63 °	1.1	0,89121	0,4536	1 96476
64 °	1,11746	0,89899	0,43797	2,05265
65 °	1,13492	0,9065	0,4222	2,14707
66 °	1,15238	0,91373	0,40631	2,24884
67 °	1,16984	0,92069	0,3903	2,35894
68 °	1,1873	0,92736	0,37416	2,4785
69 °	1,20476	0,93375	0,35792	2,60887
70 °	1,22222	0,93986	0,34156	2,75169
71 °	1,23968	0,94568	0,3251	2,90892
72 °	1,25714	0,95121	0,30854	3,08299
73 °	1,2746	0,95646	0,29188	3,27686
74 °	1,29206	0,96141	0,27514	3,49427
75 °	1,30952	0,96606	0,25831	3,73993
76 °	1,32698	0,97043	0,2414	4,0 1992
77 °	1,34444	0,97449	0,22442	4,34219
78 °	1,36191	0,97826	0,20738	4,71734
79 °	1,37937	0,98173	0,19026	5,15984
80 °	1,39683	0,98491	0,1731	5,68998
81 °	1,41429	0,98778	0,15587	6,33709
82 °	1,43175	0,99035	0,1386	7,14523
83 °	1,44921	0,99262	0,12129	8,18379
84 °	1,46667	0,99458	0,10394	9 56868
85 °	1,48413	0,99625	0,08656	11 5092
86 °	1,50159	0,99761	0,06915	14,4259
87 °	1,51905	0,99866	0,05173	19 3069
88 °	1,53651	0,99941	0,03428	29 153
89 °	1,55397	0,99986	0,01683	59,4189
90 °	1,57143	1	∞

Надеюсь, это тригонометрическое объяснение может быть вам полезно.

Этот материал будет очень полезен для различных приложений в продвинутой математике и физике.

Вы также можете изучить другие школьные материалы в Saintif, такие как простые числа, преобразование единиц измерения, прямоугольные формулы и т. Д.

Как пользоваться таблицами Брадиса

Определить тангенс и котангенс угла с помощью табличных данных достаточно просто. Рассмотрим конкретный пример:

$$tg\;10^\circ\;=\;0,1763$$

Используя специальные колонки, можно определить:

$tg\;10^\circ\;12’\;=\;0,1799,\;tg\;10^\circ\;24’\;=\;0,1835$

$tg\;50^\circ\;=\;1,1918$

С помощью дополнительной колонки можно определить, что:

$tg\;50^\circ\;12’\;=\;1,2002,\;tg\;50^\circ\;24’\;=\;1,2088$

Получить более точные показатели достаточно просто, необходимо применить поправочные коэффициенты.

$tg\;10^\circ\;15’\;=\;tg\;10^\circ\;12’\;+\;0,0009\;=\;0,1799\;+\;0,0009\;=\;0,1808$

$tg\;50^\circ\;22’\;=\;tg\;50^\circ\;24′ -0,0014\;=\;1,7705-0,0004\;=\;0,7701$

В правом столбце таблицы Брадиса, где указаны тангенсы, можно определить котангенс. В качестве альтернативы можно вычислить его с помощью тангенса угла, который дополняет искомый до 90°:

$ctg\;10^\circ\;=\;tg\;80^\circ\;=\;5,671$

Благодаря дополнительным столбцам можно определить:

$сtg\;10^\circ\;12’\;=\;5,558,\;сtg\;10^\circ\;24’\;=\;5,449$

Таким же образом можно получить результат, если посмотреть тангенс дополняющих углов: 79° 48′ и 79° 36′ соответственно.

$ctg\;50^\circ\;=\;0,8391$

В дополнительной колонке можно увидеть, что:

$ctg\;50^\circ\;12’\;=\;0,8332,\;ctg\;50^\circ\;24’\;=\;0,8273$

Другой способ — узнать тангенс дополняющих углов 39° 48′ и 39° 36′.

Особенность таблицы заключается в том, что тангенсы и котангенсы записаны в двух таблицах:

тангенсы углов от 0° до 76° (и котангенсы от 90° до 24°);
тангенсы от 76° до 90° (и котангенсы от 24° до 0°).

Примечание

Тангенсы и котангенсы разделены специально. Котангенсы, которые близки к 90° и соответствуют острым углам, сложно определить с помощью общих поправок. В связи с этим, значения записаны индивидуально.