Таблица брадиса полная

Прямоугольный треугольник

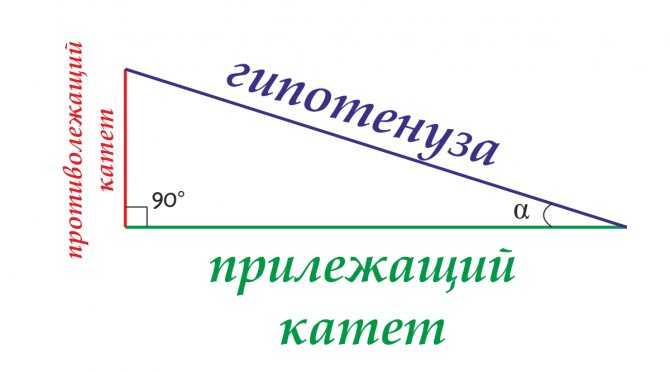
гипотенуза – сторона прямоугольного треугольника, лежащая против прямого угла и являющаяся самой длинной стороной прямоугольного треугольника.

катет – одна из сторон прямоугольного треугольника, образующая прямой угол треугольника. Может называться противолежащим или прилежащим. Противолежащий – это катет, расположенный напротив рассматриваемого угла треугольника, прилежащий – это катет, прилежащий к рассматриваемому углу треугольника.

Чтобы вычислить какой-либо неизвестный элемент (сторону или угол) имеющегося треугольника, зная часть элементов того же треугольника, используют определенные зависимости (правила) между величинами углов и длинами сторон этого треугольника. Такие зависимости называют тригонометрическими функциями.

К базовым тригонометрическим функциям относятся:

То есть, тригонометрические функций позволяют, зная какой-либо угол и сторону, вычислить значения других неизвестных элементов треугольника.

Печатать таблицу

Для печати таблицы нажмите ссылку: распечатать таблицу

Чтобы скачать эти таблицы, просто сохраните (нажмите Ctrl+S). Также смотрите таблицу косинусов.

Всё для учебы » Математика в школе » Таблица Брадиса: синусы и косинусы, тангенсы, котангенсы

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Для печати таблицы нажмите ссылку: распечатать таблицу

Таблица Брадиса: синусы и косинусы, тангенсы, котангенсы

Таблица Брадиса — это таблица, которая поможет при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах. На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов.

Пользоваться таблицами просто. Пример: найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5. Те цифры, что находятся вверху и внизу таблицы (со штрихами: ‘) это минуты. Если в задаче они тоже даны, то это лишь конкретизирует значения градусов, они необязательны для нахождения. Возможно, вам также будет интересна полная таблица синусов и таблица производных.

Пользоваться таблицами просто. Пример: найти синус тридцати градусов. Всё, что относится к синусам — вверху и слева; к косинусам — внизу и справа. Слева находим угол 30 градусов. Результат: 0.5. Те цифры, что находятся вверху и внизу таблицы (со штрихами: ‘) это минуты. Если в задаче они тоже даны, то это лишь конкретизирует значения градусов, они необязательны для нахождения. Возможно, вам также будет интересна полная таблица синусов и таблица производных.

Таблица Брадиса для тангенса и котангенса, uchim. org

Результат 0.

13.07.2017 0:52:51

2017-07-13 00:52:51

Любые данныеЛюбые данныеЛюбые данныеЛюбые данные Любые данные Любые данные

Как пользоваться таблицами Брадиса

Рассмотрим таблицу Брадиса для синусов и косинусов. Все, что относится к синусам находится вверху и слева. Если нам нужны косинусы — смотрим на правую сторону внизу таблицы.

Для нахождения значений синуса угла нужно найти пересечение строки, содержащей в крайней левой ячейке необходимое количество градусов, и столбца, содержащего в верхней ячейке необходимое число минут.

Если точного значения угла нет в таблице Брадиса, прибегаем к помощи поправок. Поправки на одну, две и три минуты даны в крайних правых столбцах таблицы. Для нахождения значения синуса угла, которого нет в таблице, находим самое близкое к нему значение. После этого прибавляем или отнимаем поправку, соответствующую разнице между углами.

В случае, если мы ищем синус угла, который больше 90 градусов, сначала нужно воспользоваться формулами приведения, а уже потом — таблицей Брадиса.

Пример. Как пользоваться таблицей Брадиса

Пусть нужно найти синус угла 17 ° 44 ‘ . По таблице находим, чему равен синус 17 ° 42 ‘ и прибавляем к его значению поправку на две минуты:

17 ° 44 ‘ — 17 ° 42 ‘ = 2 ‘ ( н е о б х о д и м а я п о п р а в к а ) sin 17 ° 44 ‘ = 0 . 3040 + 0 . 0006 = 0 . 3046

Принцип работы с косинусами, тангенсами и котангенсами аналогичен

Однако, важно помнить о знаке поправок

При вычислении значений синусов поправка имеет положительный знак, а при вычислении косинусов поправку необходимо брать с отрицательным знаком.

Тригонометрия и тригонометрические функции

Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.

Функция – это правило, описывающее зависимость одной величины от другой.

Угол – это геометрическая фигура, образованная двумя линиями, не лежащими на одной прямой и выходящими или пересекающимися в одной точке.

Углы по своему виду могут быть:

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

В зависимости от соотношения сторон и углов, треугольники можно разделить на группы:

• По величине угла:
• прямоугольный
• тупоугольный
• остроугольный

• По длине сторон:
• равносторонний
• разносторонний
• равнобедренный

Таблицы Брадиса

Рейтинг: 4.3/5.0 (1704 проголосовавших)

Категория: Windows: Математика

Описание

Таблица Брадиса

ТАБЛИЦА БРАДИСА

Четырехзная математическая таблица Брадиса синусы, косинусы в градусах и минутах с точностью до одной минуты. Как пользоваться таблицей Брадиса sin cos пример. Значения синусов и косинусов для углов от 0 до 90 градусов.

Четырехзначная таблица Брадиса тангенсы, котангенсы от 0 до 90 градусов с точностью до одной минуты. Значения tg ctg таблица. Как пользоваться таблицей брадиса примеры. Таблица разбита на две части. В первой части таблицы Брадиса тангенсы от 0 до 75 и котангенсы от 15 до 90 градусов находятся при помощи дополнительных столбцов для 1, 2 и 3 минут. Во второй части тангенсы от 75 до 90 градусов и котангенсы от 0 до 15 градусов записаны прямо в таблицу с точностью до 1 минуты угла.

Математическая четырехзначная таблица синусов, косинусов, тангенсов в радианах. Значения sin, cos, tg от 0 до 3,14 радиан с точностью до 0,01 радиана.

Смотрите так же:

Таблица значений тригонометрических функций — синусы, косинусы, тангенсы и котангенсы значения с дробями и корнями, тригонометрический круг картинка и знаки тригонометрических функций.

Тригонометрическая таблица и тригонометрический круг — интерактивная карта, угол вращаете курсором и смотрите значания функций для этого угла.

Таблица синусов от 0 до 360 градусов.

07 февраля 2012 года.

Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов

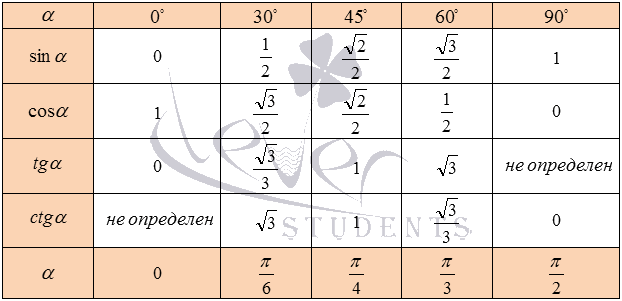
Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов: , а котангенс нуля градусов не определен, и , а тангенс 90 градусов не определен.

В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов: , и .

Занесем указанные значения тригонометрических функций для углов 0 , 30 , 45 , 60 и 90 градусов ( 0 , π/6 , π/4 , π/3 , π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.

Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120 , 135 , 150 , 180 , 210 , 225 , 240 , 270 , 300 , 315 , 330 и 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.

Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.

Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.

Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов?

Использовать таблицу синусов, косинусов, тангенсов и котангенсов основных углов 0, 30, 45, 60, 90, …, 360 градусов очень просто – она дает непосредственные значения тригонометрических функций, находящиеся на пересечении соответствующей строки, указывающей название тригонометрической функции, и столбца, указывающего данное значение угла.

Например, значение косинуса угла 60 градусов находится на пересечении строки, в крайней левой ячейке которой находится запись cos , и столбца, в верхней ячейке которого записан угол 60 градусов. Так из таблицы находим, что значение косинуса 60 градусов равно одной второй. Для разъяснения приведем графическую иллюстрацию.

Расширенная таблица основных значений тригонометрических функций используется аналогично. С помощью расширенной таблицы основных значений синуса, косинуса, тангенса и котангенса можно сразу указать, например, чему равен тангенс угла 1 020 градусов. Он равен минус корню из трех, так как . Проиллюстрируем это.

Вычисление значений углов по окружности

Самый простой и понятный способ для вычисления углов и радиан.

Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:

Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.

\
\[
\sin (\alpha+360 \cdot n)=\sin \alpha /
\]

Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.

\

Прямоугольный треугольник

гипотенуза – сторона прямоугольного треугольника, лежащая против прямого угла и являющаяся самой длинной стороной прямоугольного треугольника.

катет – одна из сторон прямоугольного треугольника, образующая прямой угол треугольника. Может называться противолежащим или прилежащим. Противолежащий – это катет, расположенный напротив рассматриваемого угла треугольника, прилежащий – это катет, прилежащий к рассматриваемому углу треугольника.

Чтобы вычислить какой-либо неизвестный элемент (сторону или угол) имеющегося треугольника, зная часть элементов того же треугольника, используют определенные зависимости (правила) между величинами углов и длинами сторон этого треугольника. Такие зависимости называют тригонометрическими функциями.

К базовым тригонометрическим функциям относятся:

То есть, тригонометрические функций позволяют, зная какой-либо угол и сторону, вычислить значения других неизвестных элементов треугольника.

Тригонометрические функции в прямоугольном треугольнике[править | править код]

Рис. 2 Прямоугольный треугольник

Чтобы определить тригонометрические функции произвольного угла α,\alpha, возьмём произвольный прямоугольный треугольник, содержащий угол α\alpha (см. Рис. 2). Стороны этого треугольника мы будем называть так:

• Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c.c.
• Противолежащий катет — катет, лежащий напротив угла. Например, катет aa — противолежащий по отношению к углу A.A.
• Прилежащий катет — катет, являющийся стороной угла. Например, катет bb — прилежащий по отношению к углу A.A.

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π.\pi. Это означает, что углы между катетами и гипотенузой лежат между и π2.\frac{\pi}{2}. Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Синус угла — отношение противолежащего катета к гипотенузе: sin Синус α=ac.\sin\alpha=\frac{a}{c}. Это отношение не зависит от выбора треугольника ABC{ABC}, содержащего угол α,\alpha, так как все такие треугольники подобны.

Косинус угла — отношение прилежащего катета к гипотенузе: cos Косинус α=bc.\cos\alpha=\frac{b}{c}. Так как sin Синус β=bc,\sin\beta=\frac{b}{c}, синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Тангенс угла — отношение противолежащего катета к прилежащему: tg Тангенс α=ab.\tg\,\alpha=\frac{a}{b}.

Котангенс угла — отношение прилежащего катета к противолежащему: ctg Котангенс α=ba.\ctg\,\alpha=\frac{b}{a}. Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Секанс угла — отношение гипотенузы к прилежащему катету: sec Секанс α=cb.\sec\alpha=\frac{c}{b}.

Косеканс угла — отношение гипотенузы к противолежащему катету: cosec Косеканс α=ca.\cosec \,\alpha=\frac{c}{a}.

Из определений тригонометрических функций следует:
a=csin Синус α,a=c\sin\alpha\,,b=ccos Косинус α,b=c\cos\alpha\,,a=btg Тангенс α,a=b\,\tg\,\alpha,b=actg Котангенс α,b=a\,\ctg\,\alpha,c=bsec Секанс α,c=b\sec\alpha\,,c=acosec Косеканс α,c=a\,\cosec \,\alpha,

и симметрично:
b=csin Синус β,b=c\sin\beta\,,a=ccos Косинус β,a=c\cos\beta\,,b=atg Тангенс β,b=a\,\tg\,\beta,a=bctg Котангенс β,a=b\,\ctg\,\beta,c=asec Секанс β,c=a\sec\beta\,,c=bcosec Косеканс β.c=b\,\cosec \,\beta.

Что такое таблица Брадиса

Использование калькуляторов при сложных расчетах (например, формулах с применением логарифмов) сегодня считается стандартом по умолчанию. Но еще 20-30 лет назад, когда вычислительная техника была распространена не так сильно, на помощь приходили другие способы вычислений — с помощью специальных таблиц, логарифмической линейки или арифмометра.

Определение

Таблица Брадиса — математическое пособие, в котором собраны таблицы, необходимые для работы по курсу математики и для практических вычислений, созданное Владимиром Модестовичом Брадисом.

Свое название они получили от брошюры «Четырехзначные математические таблицы», составленной Владимиром Брадисом. Книга неоднократно переиздавалась в советское время большими тиражами (до 500 000 экземпляров) и широко использовалась в учебном процессе — на уроках алгебры, геометрии и физики.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Точность расчётов

Особенность ряда Тейлора в том, что это бесконечный ряд — а значит, и вычисления тоже придётся делать бесконечно. Чтобы обойти это ограничение, используют погрешность — с какой точностью нам нужно посчитать значение формулы. Для этого делают так:

• Определяем точность, например 7 знаков после запятой.
• Минимальное число из 7 знаков после запятой — это 0,0000001. Это и будет наша погрешность.
• Считаем очередное слагаемое ряда Тейлора.
• Если это слагаемое меньше нашей погрешности — прибавляем и останавливаемся, потому что мы достигли нужного результата. Если не меньше — продолжаем.

С таким подходом можно найти синус любого угла с любой точностью, главное, чтобы у компьютера хватило памяти на все эти вычисления.

Что такое синус и зачем он нужен?

Вульгарное объяснение: синус — это математическая коробка, в которую засовывают любое число, а она в ответ выдаёт числа от −1 до 1. Если эти числа выстроить подряд на некой оси, то получится кривая вот такого вида:

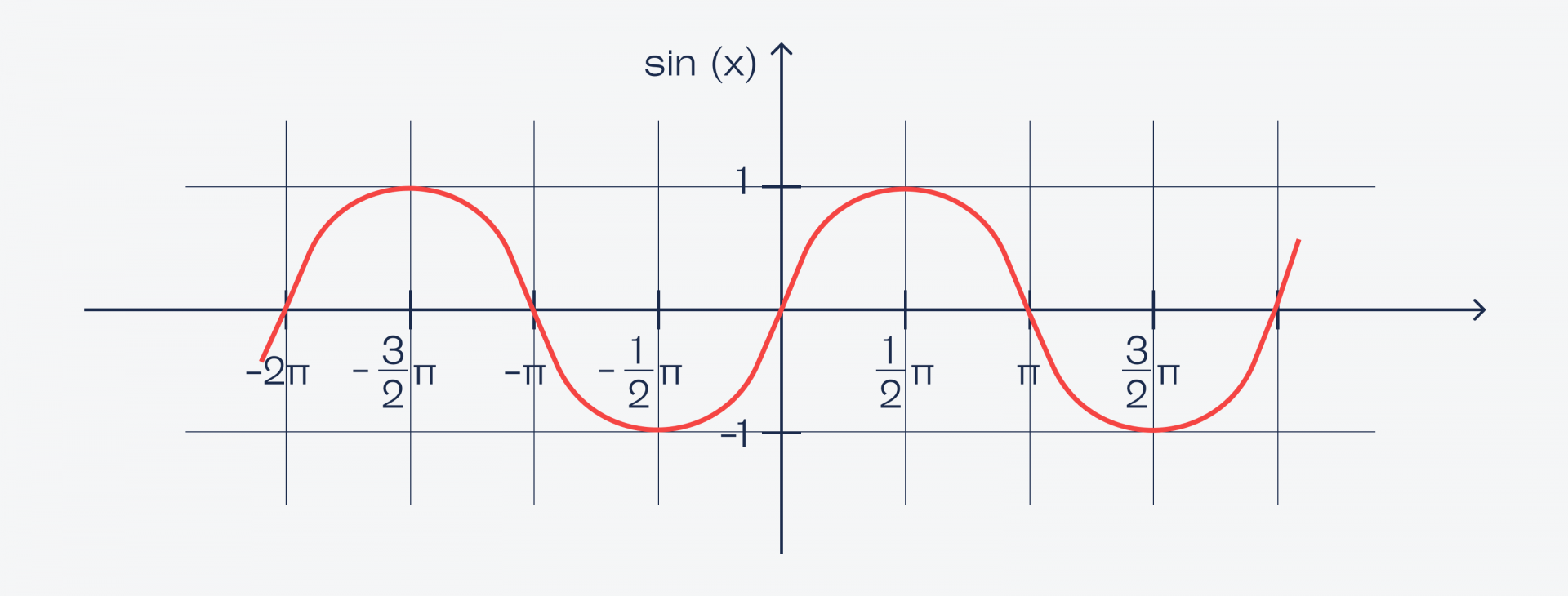
Как читать эту кривую: если затолкать в коробку «sin» число, примерно равное 1,57, то коробка выдаст число, близкое к единице. Если затолкать число 2, на выходе будет примерно 0,909. Если затолкать примерно 3,14 — вернёт примерно 0. Синус от 4,712 даст примерно −0,999. И так дальше: число может быть сколько угодно большим, а синус всегда будет возвращать какие-то дробные значения от −1 до 1.

Это число взято из тригонометрии — то есть из науки, которая занимается углами и сторонами треугольника. В частности, синус описывает отношение сторон прямоугольного треугольника: насколько один из катетов (короткая сторона треугольника) короче, чем гипотенуза (длинная сторона треугольника). Но чаще всего мы знаем не длины сторон, а угол между ними, поэтому в синусы всегда запихивают значения углов.

Грубо говоря, вы говорите коробке: «Коробка, у меня тут прямоугольный треугольник. Я смотрю на его острый угол, он равен 30º. Что ты мне на это скажешь»? А коробка отвечает: «Если у тебя угол 30º, то короткая сторона твоего треугольника вдвое короче, чем длинная гипотенуза. Так что sin(30º) = ½». 

Это число нужно много где в математике и компьютерах. Например, без синуса невозможно соединить две точки прямой линией на плоскости. Люди это делают без труда с помощью линейки, а компьютеру нужно очень чётко считать, куда поставить пиксель, и для этого нужен синус.

Помимо синуса есть ещё три аналогичные функции — косинус, тангенс и котангенс. Они такие же по принципу работы, но описывают отношения других сторон.

Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов

Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов: , а котангенс нуля градусов не определен, и , а тангенс 90 градусов не определен.

В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов: , и .

Занесем указанные значения тригонометрических функций для углов 0 , 30 , 45 , 60 и 90 градусов ( 0 , π/6 , π/4 , π/3 , π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.

Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120 , 135 , 150 , 180 , 210 , 225 , 240 , 270 , 300 , 315 , 330 и 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.

Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.

Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.

Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов?

Использовать таблицу синусов, косинусов, тангенсов и котангенсов основных углов 0, 30, 45, 60, 90, …, 360 градусов очень просто – она дает непосредственные значения тригонометрических функций, находящиеся на пересечении соответствующей строки, указывающей название тригонометрической функции, и столбца, указывающего данное значение угла.

Например, значение косинуса угла 60 градусов находится на пересечении строки, в крайней левой ячейке которой находится запись cos , и столбца, в верхней ячейке которого записан угол 60 градусов. Так из таблицы находим, что значение косинуса 60 градусов равно одной второй. Для разъяснения приведем графическую иллюстрацию.

Расширенная таблица основных значений тригонометрических функций используется аналогично. С помощью расширенной таблицы основных значений синуса, косинуса, тангенса и котангенса можно сразу указать, например, чему равен тангенс угла 1 020 градусов. Он равен минус корню из трех, так как . Проиллюстрируем это.

Основные способы, которые помогут заполнить таблицу функций

1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.

В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.

Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции

Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec)

2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение \ и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя   \ можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.

Для наглядности все прописанные действия, можно разобрать на конкретном примере.

Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении \ записываем значение угла.

Получаем следующую запись: \. Затем, проводим те же операции для заполнения оставшихся пустых строк.

\

Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.

3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется  1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.

4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. \. Выходим что искомое значение равно данному выражению.  Если \[\operatorname{tg} 45^{\circ}=\frac{\sin }{\cos }=\frac{\sqrt{1}}{2} / \frac{\sqrt{3}}{2}=\frac{1}{\sqrt{3}} .\]

Аналогично поступаем и далее.

5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.

\

Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.

\

Таблицы значений синусов, косинусов, тангенсов, котангенсов (sin, cos, tg, ctg)

Таблицы значений синусов (sin), косинусов (cos), тангенсов (tg), котангенсов (ctg) — это мощный и полезный инструмент, помогающий решать множество задач, как теоретического, так и прикладного характера. В этой статье мы приведем таблицу основных тригонометрических функций (синусов, косинусов, тангенсов и котангенсов) для углов 0, 30, 45, 60, 90, . 360 градусов ( 0 , π 6 , π 3 , π 2 , . . . , 2 π радиан). Также будут показаны отдельные таблицы Брадиса для синусов и косинусов, тангенсов и котангенсов с пояснением, как их использовать для нахождения значений основных тригонометрических функций.