Формулы суммы и разности тригонометрических функций: как преобразовать в произведение

Как вспомнить забытую тригонометрическую формулу? Вывести!

На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии.

Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами.

На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.

А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела.

Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот.

Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.

Будем опираться на следующие формулы:

1. Основное тригонометрическое тождество: sin2a+cos2a = 1
2. Определение тангенса:
3. Определение котангенса:
4. Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
5. Формула косинуса суммы: cos(a+b) = cosacosb-sinasinb

Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:

1. Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb-cosasinb
2. Косинус разности: cos(a-b) = cosacos(-b)-sinasin(-b) = cosacosb+sinasinb

Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:

1. Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
2. Косинус двойного угла: cos2a = cos(a+a) = cosacosa-sinasina = cos2a-sin2a

Аналогично получаются и формулы других кратных углов:

1. Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a-sin2a)sina = 2sinacos2a+sinacos2a-sin3a = 3sinacos2a-sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
2. Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa-sin2asina = (cos2a-sin2a)cosa-(2sinacosa)sina = cos3a-sin2acosa-2sin2acosa = cos3a-3sin2acosa = cos3a-3(1-cos2a)cosa = 4cos3a-3cosa

Прежде чем двигаться дальше, рассмотрим одну задачу. Дано: угол — острый. Найти его косинус, если Решение, данное одним учеником:

Т.к. , то sina = 3,а cosa = 4.

(Из математического юмора)

Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:

1. Связь тангенса и косинуса:

1. Аналогично получаем связь котангенса и синуса:

Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:

1. Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:

Сразу выводится и

1. Формула тангенса двойного угла:

Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла: cos2a = cos2a-sin2a прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.

cos2a+1 = cos2a-sin2a+cos2a+sin2a

2cos2a = cos2a+1 Выражая cosa через cos2a и выполняя замену переменных, получаем:

1. Косинус половинного угла:

Знак берётся в зависимости от квадранта.

Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим: cos2a-1 = cos2a-sin2a-cos2a-sin2a 2sin2a = 1-cos2a

1. Cинус половинного угла:

И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y.

Тогда sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.

Поскольку a = x+y, b = x-y, то . Поэтому

1. Представление суммы синусов в виде произведения:

Сразу же можно вывести

1. Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))

Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

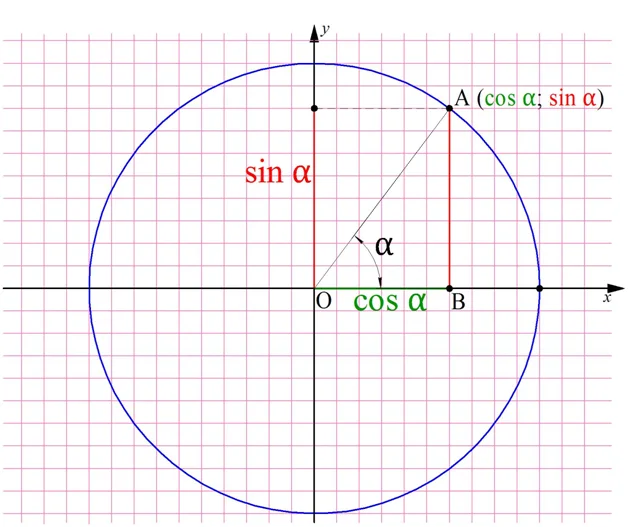
Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ2 + ОВ2 = ОА2

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin2α + соs2α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin2α + соs2α = 1

0,82 + соs2α = 1

0,64 + соs2α = 1

соs2α = 1 – 0,64

соs2α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

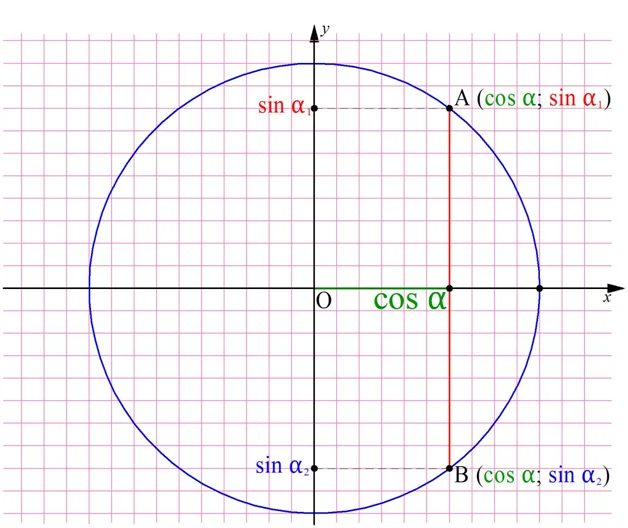
По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.

Решение.

sin2α + соs2α = 1

0,282 + sin2α = 1

0,0784 + sin2α = 1

sin2α = 1 – 0,0784

sin2α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin2α + соs2α = 1

соs2α = 1 – sin2α = 1 – (5/13)2 = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin2α + соs2α = 1

Далее поделим его на величину соs2α:

Крайнее левое слагаемое – это величина tg2α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin2α:

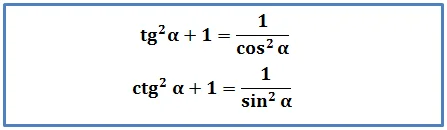
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin2α + соs2α = 1

sin2α = 1 – соs2α = 1 – (– 0,8)2 = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin2α + соs2α = 1 несложно получить из выражения

sin2α = 1 – соs2α

и

соs2α = 1 – sin2α

которые помогают в работе с длинными ф-лами.

Задание. Упростите выражение

4sin2α + 9соs2α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin2α = 1 – соs2α:

4sin2α+ 9соs2α – 6 = 4(1 – соs2α)+ 9соs2α – 6 =

= 4 – 4 соs2α + 9соs2α – 6 = 5соs2α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs2α – 2.

Задание. Избавьтесь от синуса в выражении

sin4α – соs4α

Решение. Воспользуемся ф-лой :

sin4α – соs4α = (sin2α – соs2α)(sin2α + соs2α) = (sin2α – соs2α)•1 =

= 1 – соs2α– соs2α = 1 – 2 соs2α

Ответ:1 – 2 соs2α.

Задание. Упростите дробь

Решение.

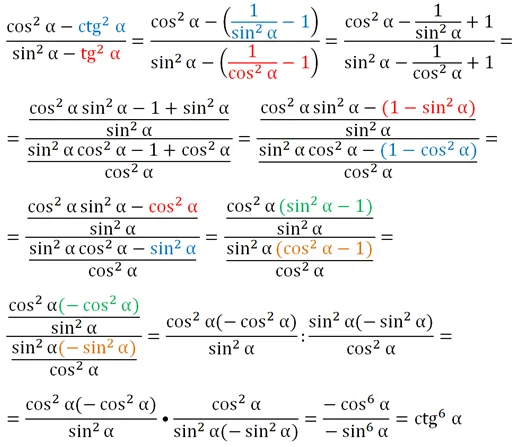
Ответ: ctg6α.

Основные тригонометрические формулы

В этой статье представлен оптимальный набор тригонометрических формул, которые необходимо знать. Все остальные тригонометрические формулы выводятся из них путем несложных преобразований.

1. Основное тригонометрическое тождество:

2. Формулы, позволяющие выразить тригонометрические функции одного аргумента одну через другую.

3. Тригонометрические формулы суммы  и разности аргументов.

4. Тригонометрические функции двойного аргумента:

5. Формулы понижения степени:

6. Тригонометрические функции половинного аргумента:

7.  Формулы универсальной подстановки:

8. Преобразование суммы или разности тригонометрических функций в произведение

9. Преобразование произведения тригонометрических функций в сумму или разность.

10. Преобразование выражения   к виду

,

где ,

Скачать таблицу формулы тригонометрии

формулы тригонометрии (2)

И.В. Фельдман, репетитор по математике.

(Ф. Хаусдорф.)

‘
quotes=’»Математика — это язык, на котором написана книга природы.»

(Г. Галилей)

‘
quotes=’»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает на­стойчивость и упорство в достижении цели.»

(А. Маркушевич)

‘
quotes=’»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»

(А.Н. Крылов)

‘ quotes=’»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»

(М.И. Калинин)

‘
quotes=’»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»

(Платон)

‘
quotes=’»Математика есть лучшее и даже единственное введение в изу­чение природы.»

(Д.И. Писарев)

‘
quotes=’»Вдохновение нужно в геометрии не меньше, чем в поэзии.»

(А.С. Пушкин)

‘
quotes=’»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»

(В. Произволов)

‘
quotes=’»В математике есть своя красота, как в живописи и поэзии.»

(Н.Е. Жуковский)

‘
quotes=’»Химия – правая рука физики, математика – ее глаз.»

(М.В. Ломоносов)

‘
quotes=’»Математику уже затем учить надо, что она ум в порядок приводит.»

(М.В. Ломоносов)

‘
quotes=’»Математика — это язык, на котором говорят все точные науки.»

(Н.И. Лобачевский)

‘
quotes=’»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»

(Л. Эйлер)

‘
quotes=’»Числа не управляют миром, но они показывают, как управляется мир.»

(И. Гете)

‘
quotes=’»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»

(В.Ф. Каган)

‘
quotes=’»Счет и вычисления — основа порядка в голове.»

(Песталоцци)

‘
quotes=’»Величие человека — в его способности мыслить.»

(Б. Паскаль)

‘
quotes=’»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»

(Д.Пойа)

‘
quotes=’»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»

(Б. Паскаль)

‘
quotes=’»В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.»

(И. Ньютон)

‘
quotes=’»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»

(Л. Карно)

‘
quotes=’»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.»

(М.В. Остроградский)

‘
quotes=’»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»

(Н.К. Крупская)

‘
quotes=’»Математика уступает свои крепости лишь сильным и смелым.»

(А.П. Конфорович)

‘
quotes=’»Доказательство — это рассуждение, которое убеждает.»

(Ю.А. Шиханович)

‘
quotes=’»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»

(И. Кант)

‘
var whichquote= Math.floor(Math.random()*(quotes.length))
document.write(quotes)

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения

1. sinα+2πz=sinα,
2. cosα+2πz=cosαtgα+2πz=tgα,
3. ctgα+2πz=ctgαsin-α+2πz=-sinα,
4. cos-α+2πz=cosαtg-α+2πz=-tgα,
5. ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα,
6. cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα,
7. ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα,
8. cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα,
9. ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα,
10. cosπ+α+2πz=-cosαtgπ+α+2πz=tgα,
11. ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα,
12. cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα,
13. ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα,
14. cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα,
15. ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα,
16. cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα,
17. ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Описание тригонометрических формул

Определения

Тригонометрия — раздел математики, который изучает зависимости между углами и сторонами треугольников.

Основные тригонометрические формулы — это формулы, устанавливающие связи между основными тригонометрическими функциями.

Термин «тригонометрия» дословно означает «измерение треугольников». Его ввел в употребление немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. Но саму тригонометрию — ее основные функции и их таблицы — придумали еще до нашей эры, в Древнем Вавилоне.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Основная функция

Чтобы производить косвенные измерения расстояний между звездами и их расположения относительно друг друга, небо представляли в виде сферы. Тогда задача сводилась к анализу треугольника, одни элементы которого можно выразить через другие. Исторически для измерения брали прямоугольные треугольники, поэтому основные функции относятся к ним. Это синус, косинус и тангенс.

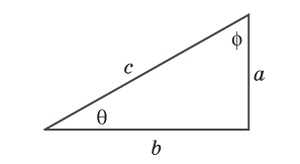
\(\sin\left(\theta\right)\;=\;\frac ас\)

\(\cos\left(\theta\right)\;=\;\frac bс\)

\(\tan\left(\theta\right)\;=\;\frac ab\;=\;\frac{\sin\left(\theta\right)}{\cos\left(\theta\right)}\)

I группа. Основные тождества

sin2α + cos2α = 1;

tgα = ____sinαcosα ;     ctgα = ____cosαsinα ;

tgα·ctgα = 1;

1 + tg2α = _____   1cos2α;     1 + ctg2α = _____   1sin2α .

Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).

Первая формула представляет собой теорему Пифагора для такого треугольника — сумма квадратов катетов равна квадрату гипотенузы (12 = 1), вторая и третья — это определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Произведение тангенса на котангенс равно 1 потому, что котангенс, записанный в виде дроби (формула третья) есть перевернутый тангенс (формула вторая). Последнее соображение, кстати, позволяет исключить из числа формул, которые необходимо обязательно заучить, все последующие длинные формулы с котангенсом. Если в каком-либо сложном задании Вам встретится ctgα, просто замените его на дробь ___  1tgα и пользуйтесь формулами для тангенса.

Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю

Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи

Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.

Примеры преобразований выражений, содержащих обратные тригонометрические функции

Пример 1.

Упростить выражение cos (arcsin х), где .

Решение:

Положим arcsin х = у. Тогда sin у = х, . Нужно найти cos у.

Известно, что
значит,
Но , а на отрезке 
косинус принимает лишь неотрицательные значения. Поэтому  т.е. 

Пример 2.

Вычислить .

Решение:

Положим . Тогда

Нужно вычислить

Имеем  ; значит,
Так как, далее,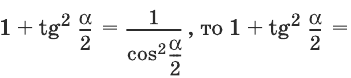
откуда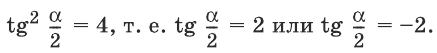

По условию,  значит,  а в интервале имеем
Итак, т. е.

Пример 3.

Доказать, что для любого х из справедливо тождество

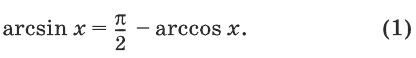
Решение:

Вычислим значения синуса левой и правой частей проверяемого равенства:

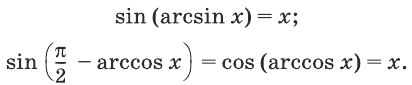
Синусы, как мы видим, равны, поэтому, чтобы убедиться в справедливости равенства (1), осталось показать, что
принадлежат одно-му и тому же промежутку монотонности функции у = sin х (без проверки этого условия можно получить неверный результат, ведь тригонометрические функции могут принимать одинаковые значения и для различных значении аргумента, например )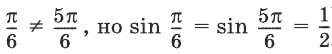

Имеем
Далее, а поэтому
Итак, arcsin х и 
принадлежат одному промежутку монотонности 
функции у = sin х. Теперь можно считать, что тождество (1) доказано. Аналогично можно доказать, что

Формулы произведения тригонометрических функций

\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}

Формулы двойного угла

`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`

Формулы половинного угла.

1. Синус половинного угла. Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части.

   Данное правило справедливо также для других формул, приведенных ниже. 

2. Косинус половинного угла:

3. Тангенс половинного угла:

4. Котангенс половинного угла:  

5. Выражение синуса через тангенс половинного угла:  

6. Выражение косинуса через тангенс половинного угла:  

7. Выражение тангенса через тангенс половинного угла:    

8. Выражение котангенса через тангенс половинного угла: 

Формулы приведения.

Функция / угол в рад.	π/2 – α	π/2 + α	π – α	π + α	3π/2 – α	3π/2 + α	2π – α	2π + α
sin	cos α	cos α	sin α	– sin α	– cos α	– cos α	– sin α	sin α
cos	sin α	– sin α	– cos α	– cos α	– sin α	sin α	cos α	cos α
tg	ctg α	– ctg α	– tg α	tg α	ctg α	– ctg α	– tg α	tg α
ctg	tg α	– tg α	– ctg α	ctg α	tg α	– tg α	– ctg α	ctg α
Функция / угол в °	90° – α	90° + α	180° – α	180° + α	270° – α	270° + α	360° – α	360° + α

Подробное описание формул приведения.

Основные тригонометрические формулы.

Основное тригонометрическое тождество:

sin2α+cos2α=1 

Данное тождество − результат применения теоремы Пифагора к треугольнику в единичном тригонометрическом круге.

Соотношение между косинусом и тангенсом:

1/cos2α−tan2α=1 или sec2α−tan2α=1. 

Данная формула является следствием основного тригонометрического тождества и получается из него делением левой и правой части на cos2α. Предполагается, что α≠π/2+πn,n∈Z.

Соотношение между синусом и котангенсом:

1/sin2α−cot2α=1 или csc2α−cot2α=1. 

Эта формула также следует из основного тригонометрического тождества (получается из него делением левой и правой части на sin2α. Здесь предполагается, что α≠πn,n∈Z.

tanα=sinα/cosα, 

где α≠π/2+πn,n∈Z.

cotα=cosα/sinα, 

где α≠πn,n∈Z.

tanα⋅cotα=1, 

где α≠πn/2,n∈Z.

Определение косеканса:

cscα=1/sinα,α≠πn,n∈Z

Тригонометрические неравенства.

Простейшие тригонометрические неравенства:

sinx > a, sinx ≥ a, sinx < a, sinx ≤ a, 

cosx > a, cosx ≥ a, cosx < a, cosx ≤ a, 

tanx > a, tanx ≥ a, tanx < a, tanx ≤ a, 

cotx > a, cotx ≥ a, cotx < a, cotx ≤ a. 

Основные формулы приведения в тригонометрии

Формулы приведения позволяют перейти от работы с произвольными и сколь угодно большими углами к работе с углами от 0 до 90 градусов, то есть преобразовать их.

Литые формулы

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctgα+ -ctgαsinπ2 +α +2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα=tπ2-α, cosπ2-α 2πz=ctgα, ctgπ2 -α +2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπz-α α+2πz=-cosαtgπ-α+2πz=- tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3πα2+α+2πz,=cc =-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=- sinαtg3π2- α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Формулы половинного угла

`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`

Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.

Вывод их можно получить из предыдущей группы (сложения и вычитания аргументов). Например, тождества двойного угла легко получить, заменив `\beta` на `\alpha`.

Тригонометрические формулы сложения углов

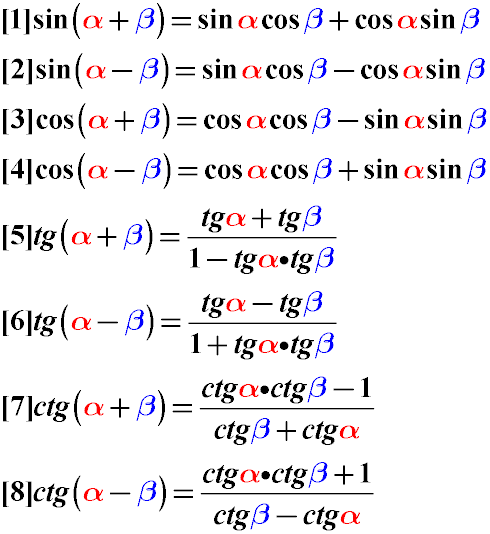
cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α — β) = sin α · cos β — sin β · cos α 
cos (α + β) = cos α · cos β — sin α · sin β 

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Формулы суммы и разности тригонометрических функций

1. Синус суммы и разности:
   $$\mathbf{\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);}$$
   $$\mathbf{\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);}$$
2. Косинус суммы и разности:
   $$\mathbf{\cos(\alpha+\beta)=\cos(\alpha)*\cos(\beta)-\sin(\beta)*\sin(\alpha);}$$
   $$\mathbf{\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);}$$
3. Тангенс суммы и разности:
   $$\mathbf{tg(\alpha+\beta)=\frac{tg(\alpha)+tg(\beta)}{1-tg(\alpha)*tg(\beta)};}$$
   $$\mathbf{tg(\alpha-\beta)=\frac{tg(\alpha)-tg(\beta)}{1+tg(\alpha)*tg(\beta)};}$$
4. Котангенс суммы и разности:
   $$\mathbf{сtg(\alpha+\beta)=\frac{-1+сtg(\alpha)*ctg(\beta)}{ctg(\alpha)+ctg(\beta)};}$$
   $$\mathbf{сtg(\alpha-\beta)=\frac{-1-сtg(\alpha)*ctg(\beta)}{ctg(\alpha)-ctg(\beta)};}$$

Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.

Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:

Пример 3
Упростить выражение \(sin(\frac{\pi}{2}+\alpha)\).

Воспользуемся формулой синуса суммы:
$$\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);$$
$$\sin(\frac{\pi}{2}+\alpha)=\sin(\frac{\pi}{2})*\cos(\alpha)+\sin(\alpha)*\cos(\frac{\pi}{2})=$$
$$=1*\cos(\alpha)+\sin(\alpha)*0=\cos(\alpha);$$

Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:

Пример 4
Найдите значение \(\sin(15^o)=?\)

\(15^o\) нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим \(15^o\) в виде разности стандартных углов \(15^o=45^o-30^o\). И воспользуемся формулой синуса разности:
$$\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);$$
$$\sin(15^o)=\sin(45^o-30^o)=\sin(45^o)*\cos(30^o)-\sin(30^o)*\cos(45^o)=$$
$$=\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
Вот мы наши синус \(15^o\). Получилось такое иррациональное некрасивое выражение, так и оставляем.

Ответ: \(\sin(15^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.\)

Пример 5
Найдите значение \(\cos(75^o)=?\)

\(75^o\) можно представить в виде суммы стандартных углов \(75^o=30^o+45^o\). Здесь воспользуемся формулой косинуса суммы:
$$\cos(\alpha+\beta)=\cos(30^o)*\cos(45^o)-\sin(30^0)*\sin(45^0)=$$
$$=\frac{\sqrt{3}}{2}*\frac{\sqrt{2}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что \(\cos(75^o)=\sin(15^o)\). Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.

Ответ: \(\cos(75^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.\)

Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.