Как измерить коэффициент мощности
Если вы не знаете точный коэфф. мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.
Для этого достаточно приобрести широко распространенный инструмент — цифровой ваттметр в розетку.
Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.
Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.
Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.
Однако это тема совсем другой статьи.
История изучения
Всегда интересно, откуда произошло то или иное слово. И только с COSINUS это очень интересная история. Он начинается в четвертом веке и связан с именем индийского астронома и математика Ариабхты.
Он ввел специальный термин, который назвал дугой. Это было слово ардхаджива, происходящее от ардха (половина) и джива (тетива).
Через 500 лет уже арабские математики решили заменить этот трудно для них произносимый термин привычным для них словом «джаиб». В переводе это означало «шишка».
И, наконец, чуть позже европейцы стали переводить арабские математические тексты и натолкнулись на этот термин. Для них слово «кливер» тоже было иностранным, поэтому они заменили его латинским «Sinus», что в переводе означает «искривление, изгиб».
Но слово КОЗИНУС является производным от СИНУС. Оно возникло из выражения «полный синус», что означает «сверхсинус» или «синус лишней дуги».
На самом деле уже тогда математики установили основную связь между синусом и косинусом. И выражается в следующей формуле:
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Низкий коэффициент мощности и его последствия
Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?
во-первых, это повышенное потребление электроэнергии
Часть энергии будет просто «болтаться» в катушке, при этом не принося никакой пользы. Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.
Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.
Зато по проводам питания будет проходить вся нагрузка, разогревая их бесполезной работой.
величина тока в проводке увеличится
Вот известное наглядное видео, демонстрирующее последствия этого для проводки.
для эл.станций и трансформаторов оно вредно перегрузкой
Казалось бы, выбрось катушку и вся проблема исчезнет. Однако делать этого нельзя.
В большинстве светильников, лампы работают не отдельно, а в паре с источниками питания. И в этих самых источниках, как раз таки присутствуют разнообразные катушки.
Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.
Поэтому характеристика коэфф. мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.
Ноль означает, что полезная работа не совершается. Единица — вся энергия идет на совершение полезной работы.
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:
Определение тригонометрических функций через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенных рядов:
sin Синус x=x−x33!+x55!−x77!+x99!+⋯=∑n=∞(−1)nx2n+1(2n+1)!,\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+\cdots=\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{(2n+1)!},cos Косинус x=1−x22+x44!−x66!+x88!+⋯=∑n=∞(−1)nx2n(2n)!.\cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}+\cdots=\sum_{n=0}^\infty\frac{(-1)^nx^{2n}}{(2n)!}.
Пользуясь этими формулами, а также уравнениями tg Тангенс x=sin Синус xcos Косинус x,\tg\,x=\frac{\sin x}{\cos x},ctg Котангенс x=cos Косинус xsin Синус x,\ctg\,x=\frac{\cos x}{\sin x},sec Секанс x=1cos Косинус x\sec x=\frac{1}{\cos x} и cosec Косеканс x=1sin Синус x,\cosec \,x=\frac{1}{\sin x}, можно найти разложения в ряд Тейлора и других тригонометрических функций:
(1)cosec Косеканс x=∑n=∞(−1)n+12(22n−1−1)B2n(2n)!x2n−1(2)=x−1+16x+7360×3+3115120×5+⋯,for <|x|<π,\begin{align}
\csc x &= \sum_{n=0}^\infty \frac{(-1)^{n+1} 2 \left(2^{2n-1}-1\right) B_{2n}}{(2n)!}x^{2n-1} \\
&= x^{-1} + \frac{1}{6}x + \frac{7}{360}x^3 + \frac{31}{15120}x^5 + \cdots, \qquad \text{for } 0 < |x| < \pi,
\end{align}
где BnB_n — числа Бернулли.
sec Секанс x=1+x22+5×424+61×6720+277×88064+⋯=∑n=∞(−1)nE2n(2n)!x2n,\sec x=1+\frac{x^2}{2}+\frac{5x^4}{24}+\frac{61x^6}{720}+\frac{277x^8}{8064}+\cdots = \sum_{n=0}^\infty\frac{(-1)^nE_{2n}}{(2n)!}x^{2n},где EnE_n — числа Эйлера.
Свойства косинуса
Ниже в табличной форме представлены основные свойства косинуса с формулами:
| Свойство | Формула |
| Симметрия | cos(-α) = cosα»порядок данных=»cos (-α) = cos α»>cos(-α) = cosα |
| Симметрия | cos (90°- α) = sin α» data-order=»cos (90°- α) = sin α»> cos (90°- α) = sin α |
| Пифагорейское тригонометрическое тождество | sin2 α + cos2 α = 1″ порядок данных=»sin2 α + cos2 α = 1″>sin2α + cos2α = 1 |
| cos α = sin α / tg α» data-order=»cos α = sin α / tg α»> cos α = sin α / tg α | |
| cos α = 1/сек α» data-order=»cos α = 1 / sec α»> cos α = 1/сек α | |
| Косинус двойного угла | cos2α = cos2α — sin2α» data-order=»cos 2α = cos2 α — sin2 α»>cos2α = cos2α — sin2α |
| Косинус суммы углов | cos (α+β) = cos α cos β — sin α sin β» data-order=»cos (α+β) = cos α cos β — sin α sin β»> cos (α + β) = cos α cos β — sin α sin β |
| Косинус разности углов | cos (α-β) = cos α cos β + sin α sin β» data-order=»cos (α-β) = cos α cos β + sin α sin β»> cos (α-β) = cos α cos β + sin α sin β |
| Сумма косинусов | |
| Косинусная разница | |
| Произведение косинусов | |
| Произведение косинуса и синуса | |
| Производная косинуса | cos’ x = -sin x» data-order=»cos’ x = -sin x»>cos’ х = -sin х |
| Интеграл косинуса | ∫ cos x dx = sin x + C»data-order=»∫ cos x dx = sin x + C»>∫ cos x dx = sin x + C |
| Формула Эйлера | cos x = (eix + e-ix) / 2″ data-order=»cos x = (eix + e-ix) / 2″> cos x = (eix + e-ix) / 2 |
Таблица косинусов для 181°-360°
|
|
|
Формулы приведения тригонометрических функций, таблица
Тригонометрические функции обладают свойством периодичности. Это позволяет сделать более полной таблицу со значениями от 0° до 90° с помощью формул приведения и находить значения тригонометрических функций для произвольно выбранных углов. Использование формул приведения сводится к переходу от произвольно выбранного угла к углу меньше 90°, значения которых уже можно легко найти в обычной таблице.
Формул приведения довольно много, и заучивать их, в основном, не требуют. В данных формулах аргументами тригонометрических функций обычно являются углы следующего вида:
- ±α+2π·z;
- π/2±α+2π·z;
- π±α+2π·z;
- 3π/2±α+2π·z, где z — любое натуральное число, а альфа — произвольный угол поворота.
Список формул приведения выглядит следующим образом:
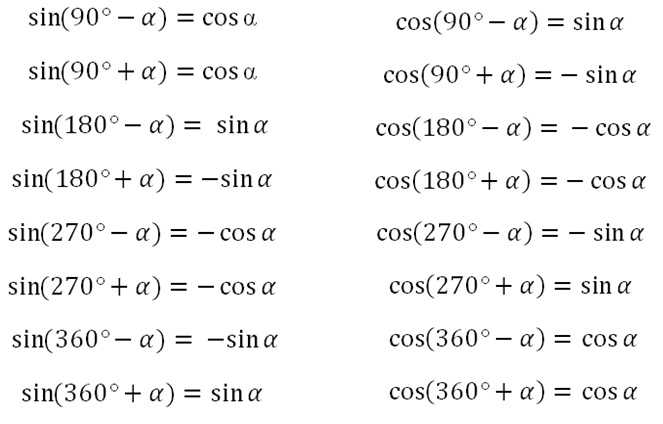
В них можно использовать как градусы, так и радианы.
Для работы с формулами приведения необходимо представить искомый угол в виде одного из перечисленных выше аргументов и подставить в формулу приведения.
Пример
Для примера возьмем угол, равный 16π/3. Его можно представить в виде π+ π/3+2 π·2, а также несколькими другими способами. Косинус данного угла в таком случае будет равен:
cos(16π/3) = cos(π+ π/3+2 π·2) = cos(π/3)
Данное значение мы уже можем найти в обычной таблице тригонометрических функций, значение cos(π/3) = 1/2.
Правило встречается в следующих упражнениях:
7 класс
Задание 591, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 642, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 704, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1024, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1037, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1117, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1238, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1307, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Функция косинуса: свойства и значения функции косинус
Определение
Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.
- Основные свойства функции косинус следующие:
- Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
- Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
- Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
- Функция чётная, т. е. cos(-x) = cos(x);
- Функция периодическая. Её период равен 2π;
- Наибольшего своего значения функция косинус x достигает в точках x=2πk;
- Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
- Область возрастания функции cos(x): -π+2πk<=x<=2πk;
- Область убывания функции cos(x): 2πk<= π+2πk;
- Функция не имеет разрывов, т. е. непрерывна.
Как пользоваться таблицей
Таблица, в которой собраны значения косинусов для углов от 0° до 360°, либо углов, выраженных в радианной мере, является информационным материалом, который используют математики и физики. С помощью данного справочного пособия удается упростить и сократить решения разных задач по алгебре, геометрии, физике, математическому анализу, тригонометрии и другим дисциплинам, где приходится часто сталкиваться с массивными вычислениями.
Пользоваться рассматриваемой таблицей достаточно просто. Стандартный алгоритм действий ее применения в решении примеров состоит в выполнении нескольких ключевых операций:
Тангенс и котангенс через синус и косинус
Несколько вступлений:
- Синус угла — это ордината у.
- Косинус угла — это абсцисса x.
- Тангенс угла – это отношение ординаты к абсциссе.
- Котангенс угла – это отношение абсциссы к ординате.
Из всего этого множества красивых, но не очень понятных слов можно сделать вывод, что одно зависит от другого. Такое соединение помогает отдельно преобразовывать нужные величины.
- tga =
- ctga =
На основании определений:
- tga =
= - ctga =
=
Это позволяет сделать вывод, что тригонометрические тождества
даны углы sin и cos.
Отсюда следует, что тангенс угла есть отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых укладываются в диапазон.
Например, выражение
относится к любому углу α, не равному
+ π + z, где z — любое целое число. В противном случае знаменатель будет равен 0.
Выражение
выполняется для любого угла α, не равного π * z, где z — любое целое число.
Курс подготовки к ОГЭ по математике Skysmart придаст вам уверенности и поможет освежить знания перед экзаменом.
Что такое коэффициент мощности
А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов.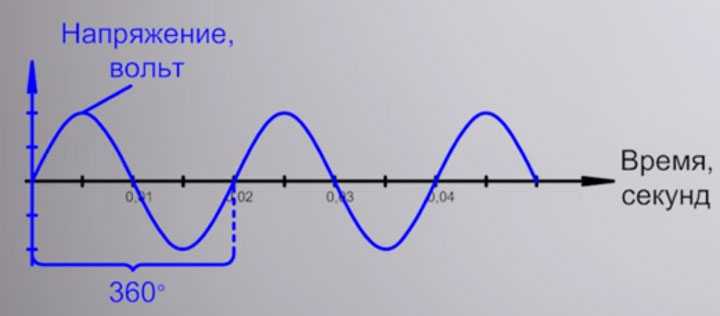
А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ.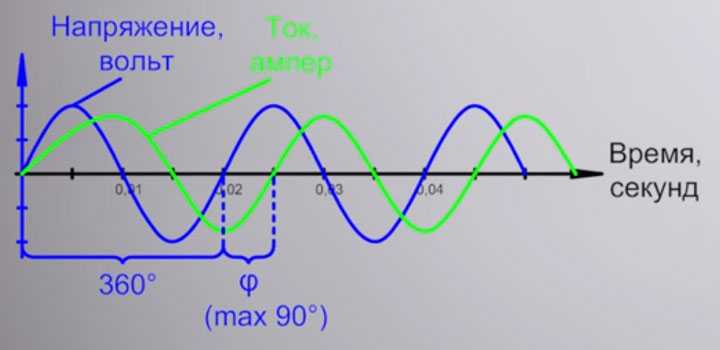
Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться.
По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.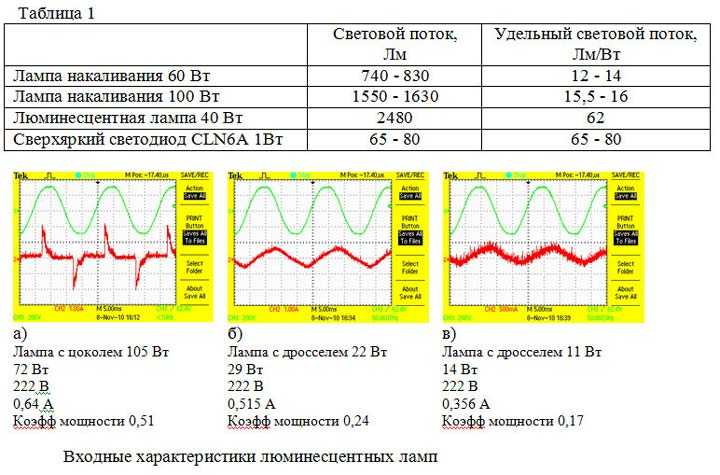
В качестве примера можно взять импульсные блоки питания.
Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности.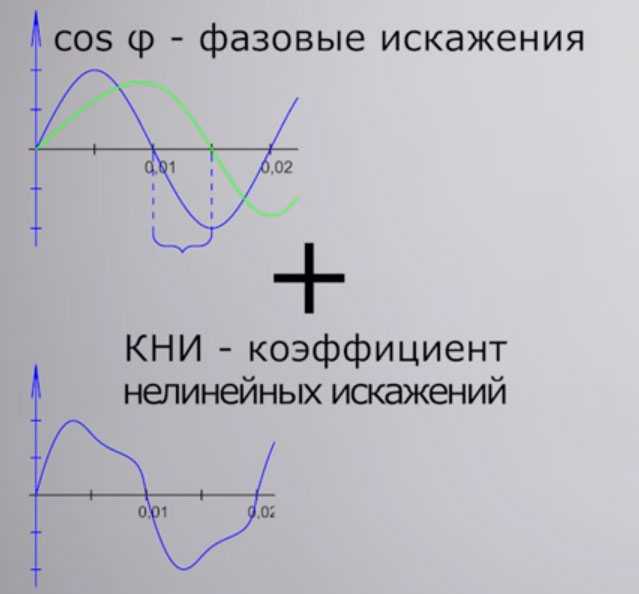
Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи.
На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной.
Таблица косинусов в радианах
Радиан представляет собой угол, который соответствует дуге с длиной, определяемой радиусом.
В радианах принято измерять плоские углы.
Радианная мера является угловой мерой, измеряемой в радианах, определяется, как отношение рассматриваемого угла к радиану.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Проанализируем данное определение. Заметим, что справедливым является вывод о величине в 2 \(\pi\) радиан, характерной для полного угла.
При решении задач по тригонометрии и геометрии часто приходится иметь дело с углами, измеряемыми в радианах. Упростить вычисление величин можно, если воспользоваться таблицей косинусов углов, для которых известна радианная мера. Кроме того, радианы нередко присутствуют в заданиях по различным темам математического анализа.
Примеры решения задач
С помощью теоремы косинусов можно решать задачи по геометрии. Рассмотрим несколько интересных случаев.
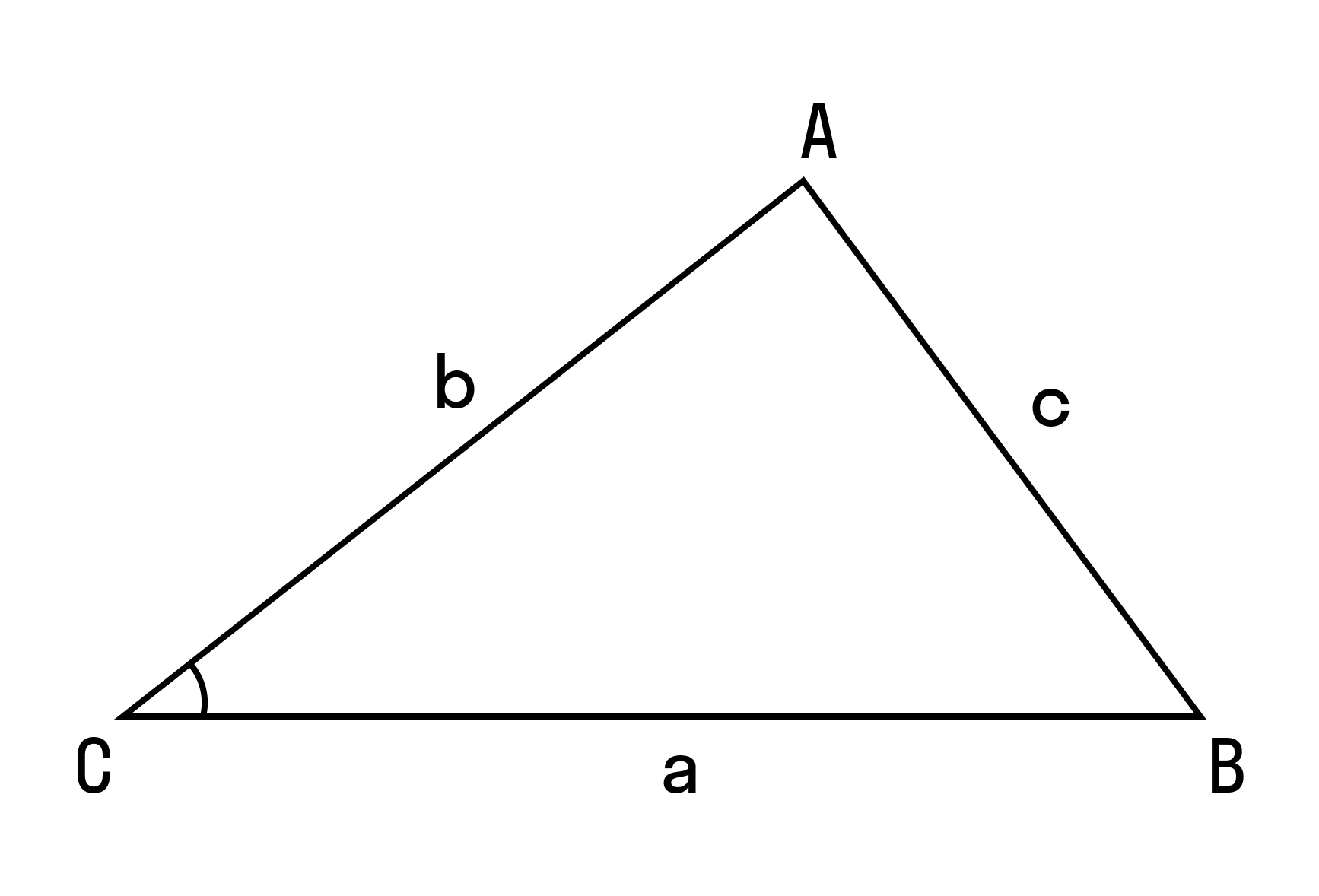
Пример 1. Дан треугольник ABC. Найдите длину см.
∠C = 90°, AB = 9, BC = 3, AM/MB = 1/2, где M — точка на гипотенузе AB.
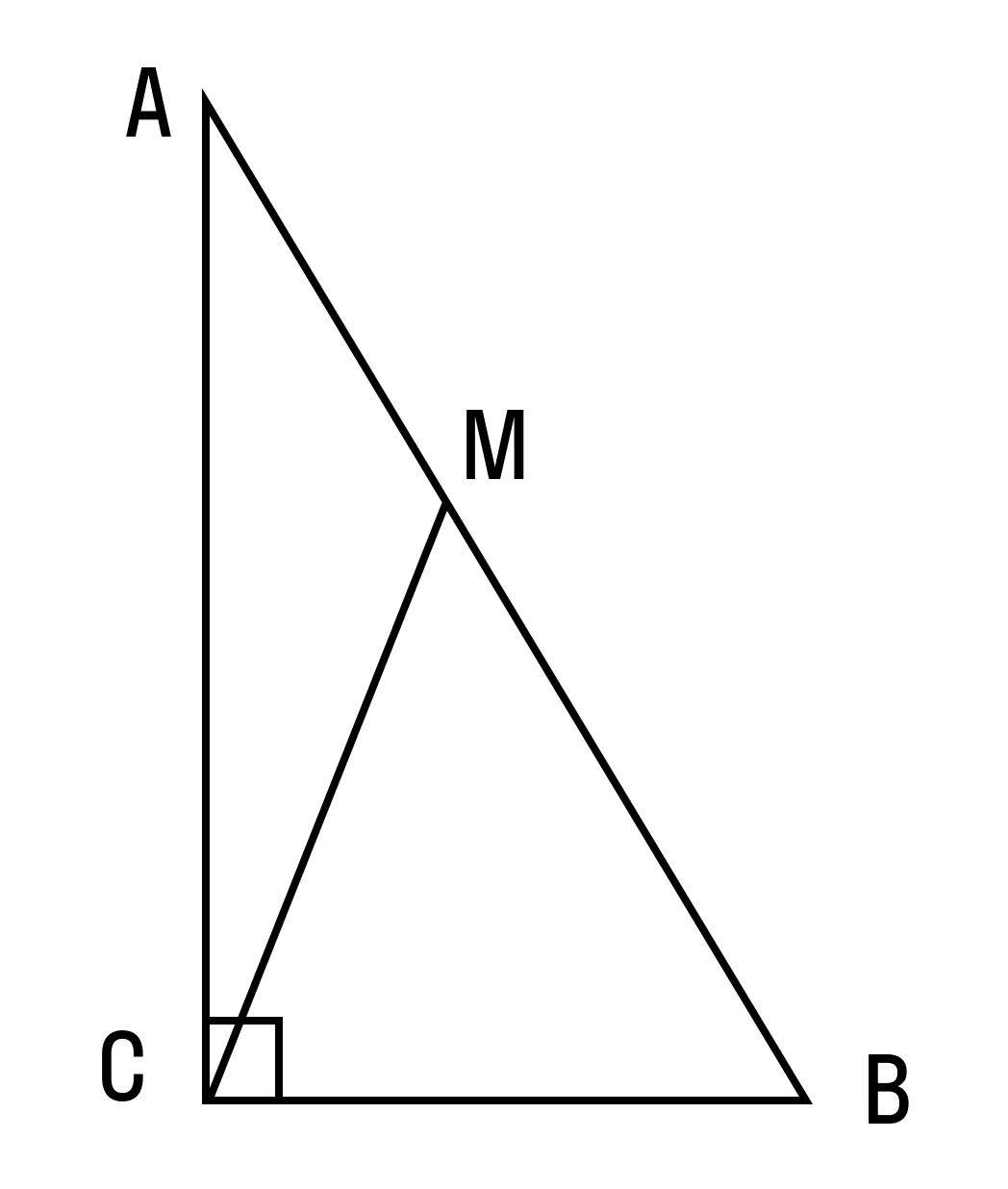
Как мы решаем:
- Поскольку АМ + МБ = 9 и АМ/МБ = 1/2, то АМ = 3, МБ = 6.
Из треугольника ABC находим cos B: -
Из треугольника CMW по теореме косинусов находим CM:
Ответ: СМ = .
Пример 2. Дан треугольник ABC, где a2 + b2 < c2. Докажите, что угол ∠C тупой.
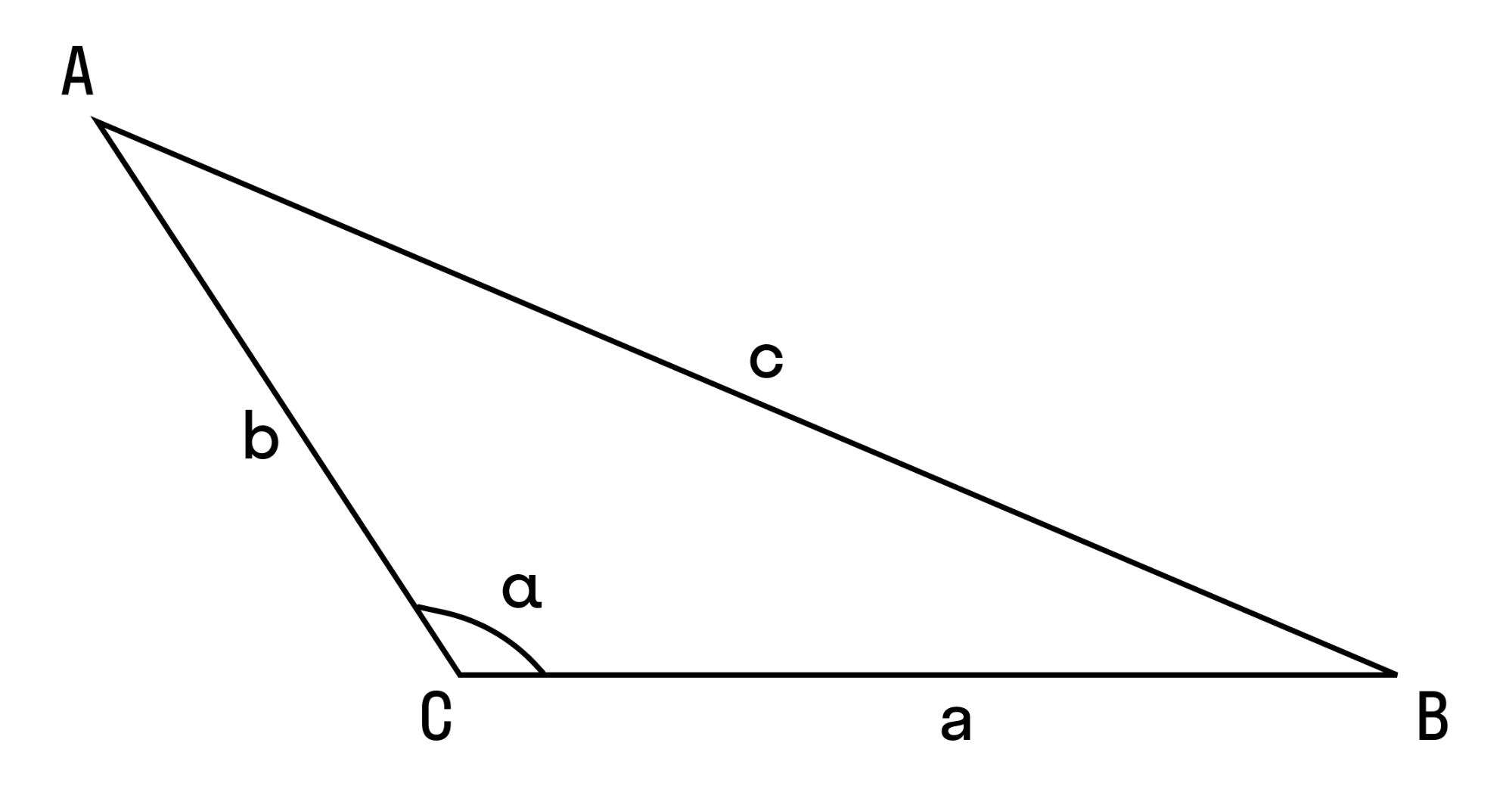
Как мы докажем:
- Чтобы это доказать, нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, поэтому ∠C тупая.
КЭД
Эта задача показала нам, что с помощью теоремы косинусов можно определить тупой или острый угол.
Если c2 = a2 + b2, то ∠C = 90°.
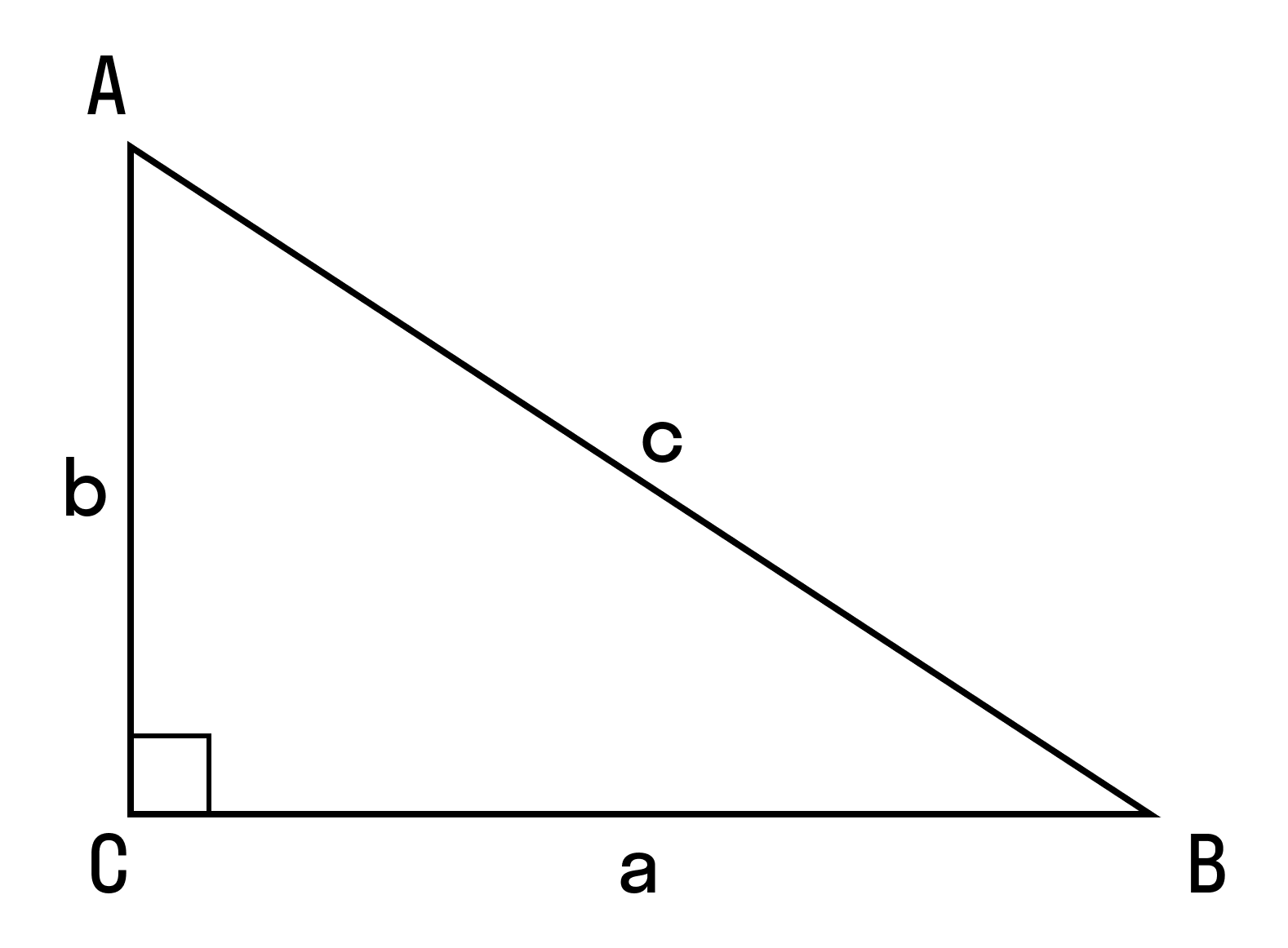
Если c2
Дополнительные пояснения по этой и другим темам можно найти в справочнике по математике — с формулами, рисунками и примерами решения задач.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, c — гипотенуза.
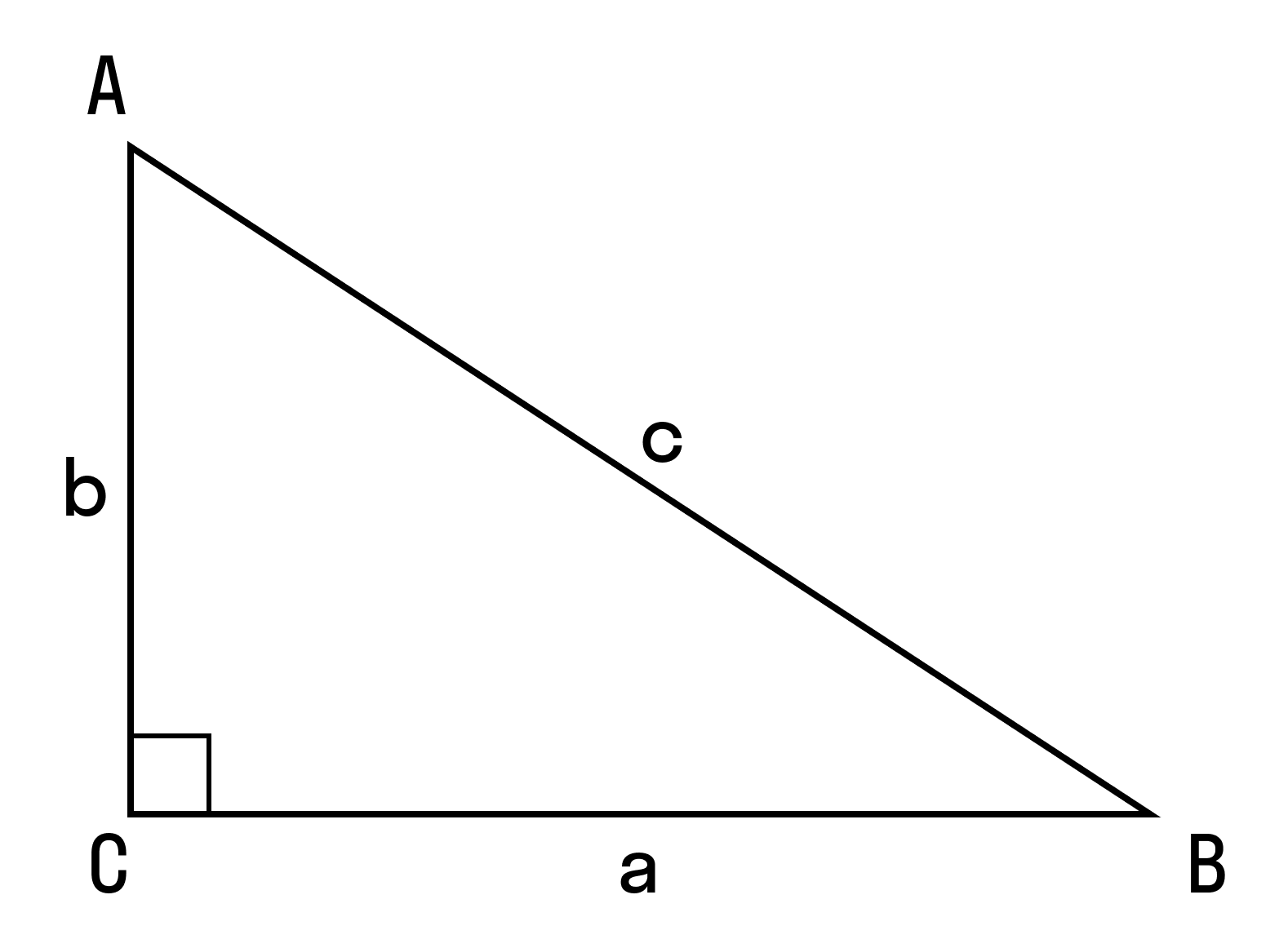
| Теорема косинусов звучит так: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α |
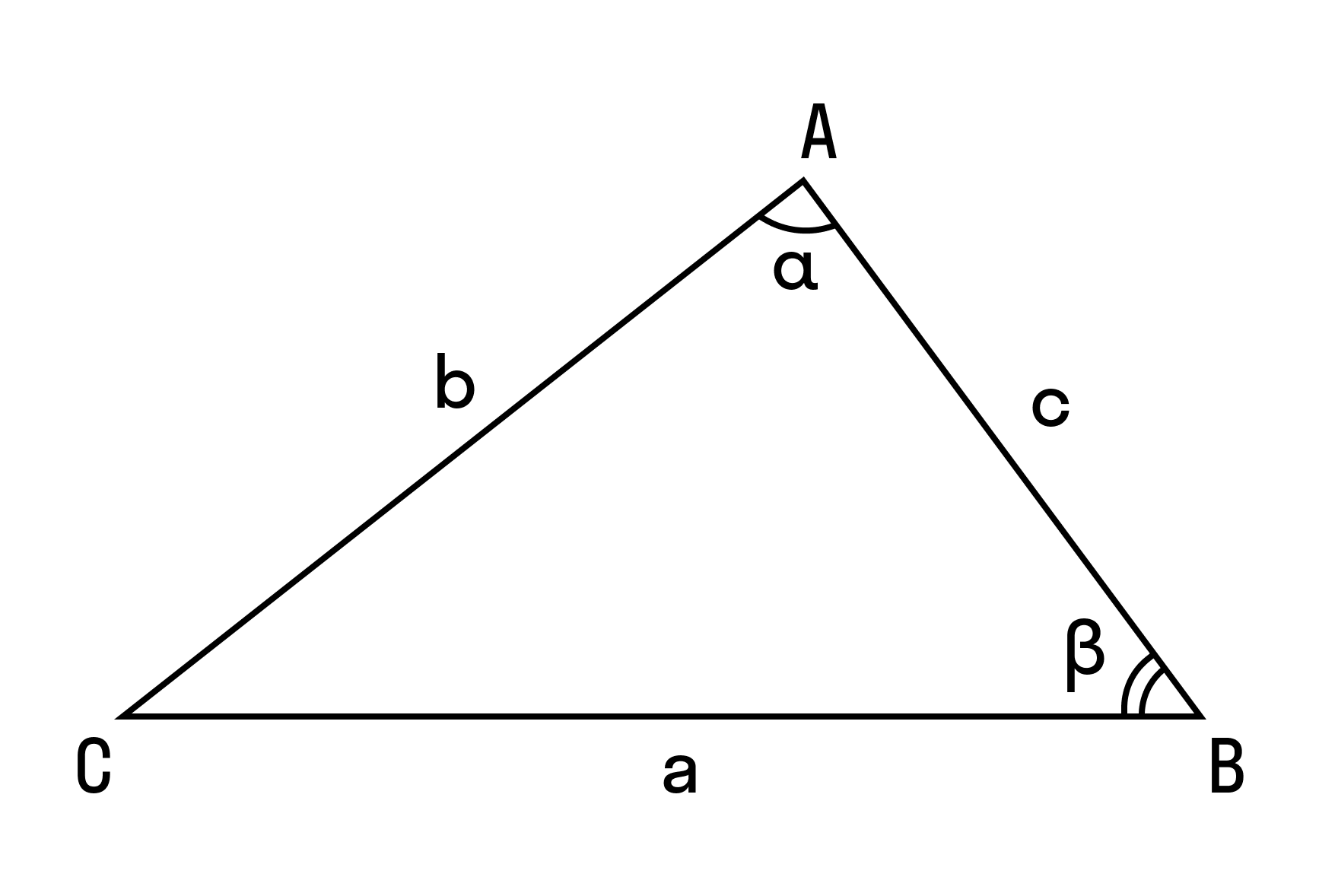
При доказательстве теоремы косинусов мы используем формулу длины отрезка в координатах. Рассмотрим эту формулу:
ВС2 = (х2 — х1)2 + (у2 — у1)2
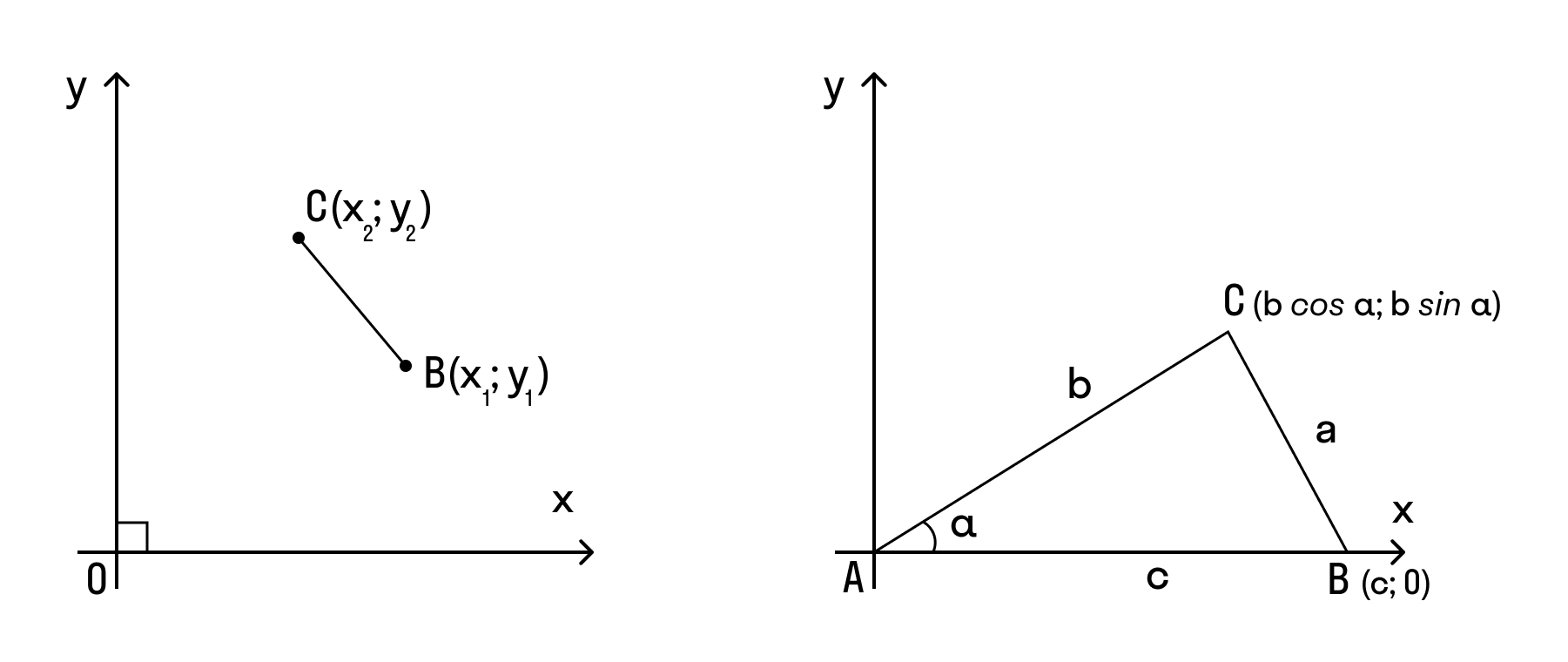
В доказательстве теоремы косинусов ВС — сторона треугольника АВС, которую обозначают буквой а. Введем практическую систему координат и найдем координаты нужных нам точек. Точка B имеет координаты (c; 0).
Координаты точки C равны (b cos α; b sin α) для α ∈ (0°; 180°).
cos2α + sin2α = 1 — основное тригонометрическое тождество.
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
КЭД
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на математические онлайн-курсы для детей и подростков.
Используя закон косинусов, можно найти косинус угла треугольника:
- При b2 + c2 — a2 > 0 угол α будет острым.
- При b2 + c2 — a2 = 0 угол α будет прямым.
- При b2 + c2 — a2 < 0 угол α будет тупым.
Помните: когда угол α прямой, теорема косинусов становится теоремой Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Получим треугольник ABC, в котором высота CD опущена от вершины C к стороне AB. Это означает:
- AD = b × cos α,
- DB = c – b × cos α.
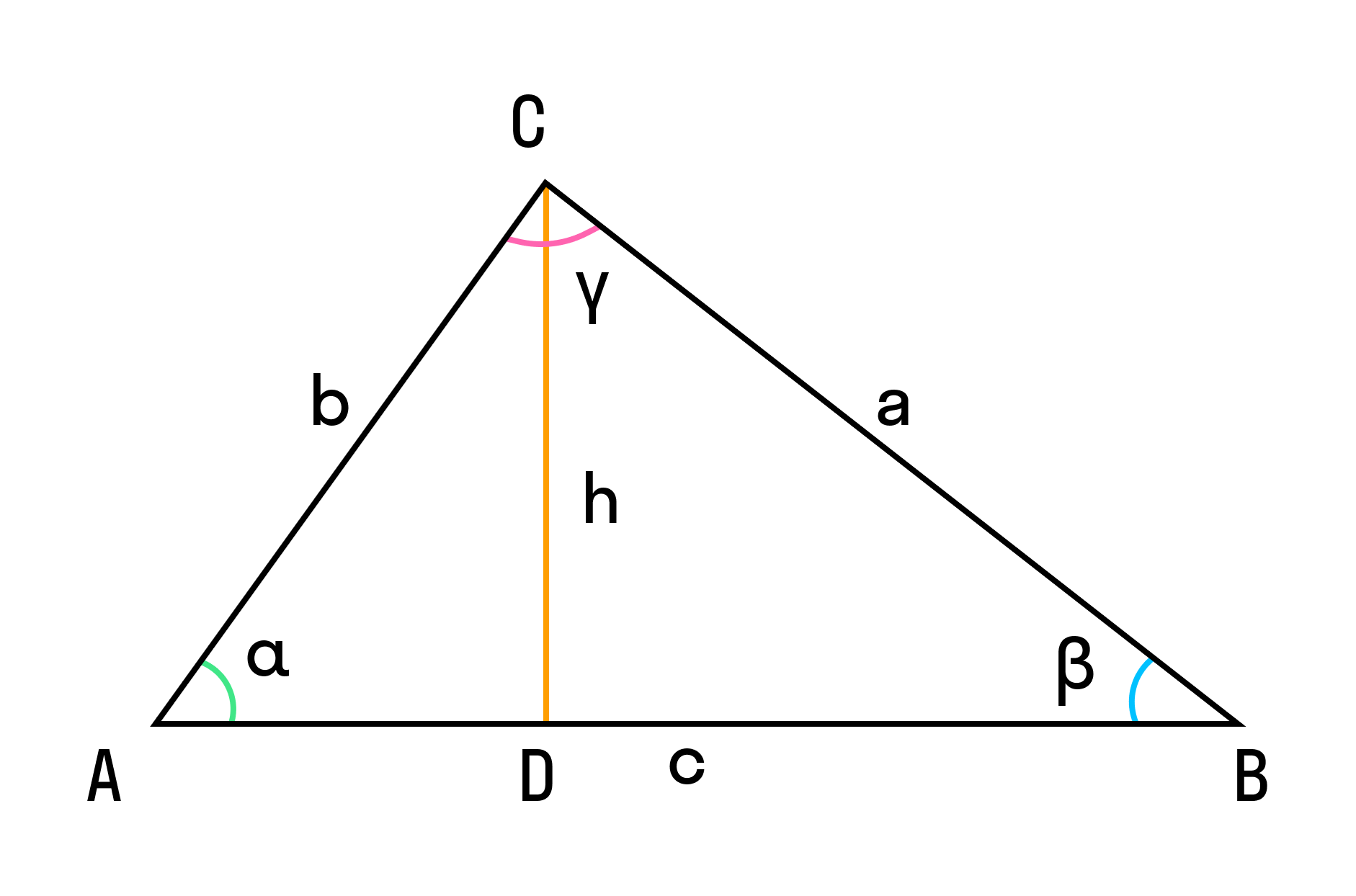
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b × cos α)2
- h2 = a2 — (c – b × cos α)2
Приравняем правильные части уравнений:
b2 — (b × cos α)2 = a2 — (c — b × cos α)2
или
a2 = b2 + c2 — 2bc × cosα
Если один из углов у основания тупой (высота упирается в продолжение основания), то это точно так же, как обсуждалось выше.
Определим стороны b и c:
- b2 = a2 + c2 — 2ac × cosβ;
- c2 = a2 + b2 — 2ab × cos γ.
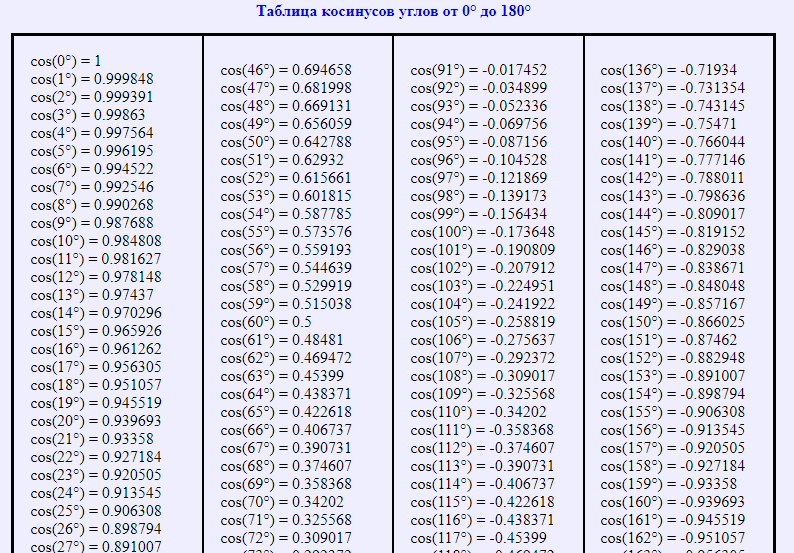
Таблица косинусов от 0° до 180°
Градусы, минуты и секунды являются общеизвестными измерительными единицами, предусмотренными для плоских углов. Угол в 360° соответствует одному полному обороту.
Градусы допустимо выражать в радианах и наоборот. Этот прием полезен для упрощения вычислений при решении задач с плоскими углами. Запишем справедливое соотношение, которое выражает зависимость между данными угловыми мерами:
\(1^{\circ }={\frac {2\pi }{\displaystyle {360}}} радиан ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}{\displaystyle \approx 0{,}0174532925}\)
Тригонометрические функции в прямоугольном треугольнике[править | править код]
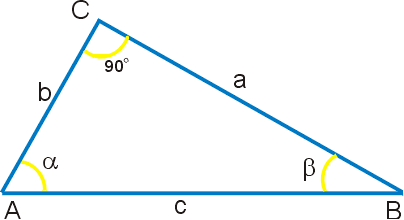Рис. 2 Прямоугольный треугольник
Чтобы определить тригонометрические функции произвольного угла α,\alpha, возьмём произвольный прямоугольный треугольник, содержащий угол α\alpha (см. Рис. 2). Стороны этого треугольника мы будем называть так:
- Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона c.c.
- Противолежащий катет — катет, лежащий напротив угла. Например, катет aa — противолежащий по отношению к углу A.A.
- Прилежащий катет — катет, являющийся стороной угла. Например, катет bb — прилежащий по отношению к углу A.A.
Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна π.\pi. Это означает, что углы между катетами и гипотенузой лежат между и π2.\frac{\pi}{2}. Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.
Синус угла — отношение противолежащего катета к гипотенузе: sin Синус α=ac.\sin\alpha=\frac{a}{c}. Это отношение не зависит от выбора треугольника ABC{ABC}, содержащего угол α,\alpha, так как все такие треугольники подобны.
Косинус угла — отношение прилежащего катета к гипотенузе: cos Косинус α=bc.\cos\alpha=\frac{b}{c}. Так как sin Синус β=bc,\sin\beta=\frac{b}{c}, синус одного острого угла в треугольнике равна косинусу второго, и наоборот.
Тангенс угла — отношение противолежащего катета к прилежащему: tg Тангенс α=ab.\tg\,\alpha=\frac{a}{b}.
Котангенс угла — отношение прилежащего катета к противолежащему: ctg Котангенс α=ba.\ctg\,\alpha=\frac{b}{a}. Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.
Секанс угла — отношение гипотенузы к прилежащему катету: sec Секанс α=cb.\sec\alpha=\frac{c}{b}.
Косеканс угла — отношение гипотенузы к противолежащему катету: cosec Косеканс α=ca.\cosec \,\alpha=\frac{c}{a}.
Из определений тригонометрических функций следует:
a=csin Синус α,a=c\sin\alpha\,,b=ccos Косинус α,b=c\cos\alpha\,,a=btg Тангенс α,a=b\,\tg\,\alpha,b=actg Котангенс α,b=a\,\ctg\,\alpha,c=bsec Секанс α,c=b\sec\alpha\,,c=acosec Косеканс α,c=a\,\cosec \,\alpha,
и симметрично:
b=csin Синус β,b=c\sin\beta\,,a=ccos Косинус β,a=c\cos\beta\,,b=atg Тангенс β,b=a\,\tg\,\beta,a=bctg Котангенс β,a=b\,\ctg\,\beta,c=asec Секанс β,c=a\sec\beta\,,c=bcosec Косеканс β.c=b\,\cosec \,\beta.