Неопределенный интеграл и его свойства: формулы и таблица

Уравнения, сводящихся к разложению на множители

Самое важное, что тебе нужно помнить, чтобы решать уравнения этого типа, это:

• Формулы приведения
• Синус, косинус двойного угла

Как показывает практика, как правило, этих знаний достаточно. Давай обратимся к примерам.

Уравнения, сводящиеся к разложению с помощью синуса двойного угла:

Уравнение 18. Ре­ши­те урав­не­ние \( \displaystyle sin2x=\text{sin}\left( \frac{\pi }{2}+x \right)\). Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку \( \displaystyle \left\)

Здесь, как я и обещал, работают формулы приведения:

\( \displaystyle \sin \left( \frac{\pi }{2}+x \right)=cosx\)Тогда мое уравнение примет вот такой вид:

\( \displaystyle sin2x=cosx\)Что дальше? А дальше обещанный мною второй пункт программы – синус двойного угла:

\( \displaystyle sin2x=2sinxcosx\)Тогда мое уравнение примет следующую форму:

\( \displaystyle 2sinxcosx=cosx\)Недальновидный ученик мог бы сказать: а теперь я сокращу обе части на \( \displaystyle cosx\), получаю простейшее уравнение \( \displaystyle 2sinx=1\) и радуюсь жизни! И будет горько заблуждаться!

Запомни!

Никогда нельзя сокращать обе части тригонометрического уравнения на функцию, содержащую неизвестную! Таки образом ты теряешь корни!

Так что же делать? Да все просто, переносить все в одну сторону и выносить общий множитель:

\( \displaystyle 2sinxcosx-cosx=0\)\( \displaystyle cosx\left( 2sinx-1 \right)=0\)Ну вот, на множители разложили, ура! Теперь решаем:

\( \displaystyle cosx=0\) или \( \displaystyle 2sinx=1\)Первое уравнение имеет корни:

\( \displaystyle x=\frac{\pi }{2}+\pi n\).

А второе:

Некоторые другие формулы

Основные формулы тригонометрии и формулы синуса арксинуса, косинуса арккосинуса, тангенса арктангенса и котангенса арккотангенса позволяют вывести ряд формул с arcsin , arccos , arctg и arcctg , еще не упомянутых в данной статье. Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.

Для примера возьмем формулу половинного угла . Если добавить условие, что величина угла альфа принадлежит отрезку от нуля до пи, то будет справедливо равенство . При указанном условии угол альфа можно заменить на арккосинус числа a , что нам даст формулу вида , откуда можно получить следующую формулу, выражающую арккосинус через арксинус: .

Используя другие тригонометрические формулы, можно обнаружить ряд других связей между arcsin , arccos , arctg и arcctg .

В заключение этого пункта хочется сказать, что практическую пользу представляют даже не столько сами эти специфические формулы, связывающие arcsin , arccos , arctg и arcctg , сколько умения выполнять преобразования, используемых при выводе этих формул. Продолжением темы служит раздел теории преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

Правила интегрирования функций

Для того чтобы взять интеграл, не всегда хватает знания таблицы основных формул, также необходимо знать свойства интегралов и правила интегрирования различных функций.

1. \(\int c\;f(x)\operatorname dx=c\int\;f(x)\operatorname dx\;\)постоянный множитель (константу) можно вынести за знак интеграла
2. \(\int\lbrack\;f(x)+g(x)\rbrack\operatorname dx=\int\;f(x)\operatorname dx\;+\int\;g(x)\operatorname dx\) интеграл от суммы функций равен сумме интегралов этих функций
3. \(\int\lbrack\;f(x)-g(x)\rbrack\operatorname dx=\int\;f(x)\operatorname dx\;-\int\;g(x)\operatorname dx\) интеграл от разности функций равен разности интегралов этих функций
4. \(\int\;u\operatorname dv\;=uv-\int v\operatorname du\) правило интегрирования по частям, где u=f(x), v=g(x)

Метод замены переменной помогает упростить сложные интегралы и свести их либо к более простым, либо к табличным значениям, которые можно сразу проинтегрировать и вычислить значения, если нам известны пределы интегрирования (для определенного интеграла). Он производится двумя способами: подведение функции под знак дифференциала и собственно замена переменной.

Использование тригонометрических формул

Пример 1

Найти неопределенный интеграл.

Сначала полное решение, потом комментарии.

Используем формулу:

(1) Мы видим, что в подынтегральном выражении находится произведение двух функций. К сожалению, в интегральном исчислении нет удобной формулы для интегрирования произведения: , поэтому приходится прибегать к различным ухищрениям. В данном случае мы прерываем решение значком  и поясняем, что используется тригонометрическая формула. Данная формула превращает произведение в сумму.

(2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла.

! Справка: При работе с тригонометрическими функциями следует помнить, что:

Косинус – это четная функция, то есть , минус исчезает без всяких последствий. В рассматриваемом примере:

Синус – функция нечетная:  – здесь минус, наоборот – не пропадает, а выносится.

(3) Под интегралами у нас сложные функции (косинусы не просто от , а от сложного аргумента). Это простейшие из сложных функций, интегралы от них удобнее найти методом подведения под знак дифференциала. Более подробно с данным приёмом можно ознакомиться на уроке Метод замены переменной в неопределенном интеграле.
(4) Используем табличную формулу , единственное отличие, вместо «икса» у нас сложное выражение.

Готово.

 Пример 2

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Пример 3

Найти неопределенный интеграл.

Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.

(1) Используем тригонометрическую формулу

(2) Подводим функцию под знак дифференциала.

(3) Используем табличный интеграл .

Пример 4

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Пример 5

Найти неопределенный интеграл.

Степени у нас будут потихоньку повышаться =).
Сначала решение:

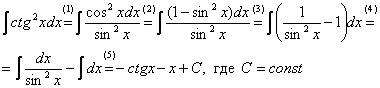
(1) Используем формулу

(2) Используем основное тригонометрическое тождество , из которого следует, что .

(3) Почленно делим числитель на знаменатель.

(4) Используем свойство линейности неопределенного интеграла.

(5) Интегрируем с помощью таблицы.

Пример 6

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Также существуют интегралы от тангенсов и котангенсов, которые находятся в более высоких степенях. Интеграл от тангенса в кубе рассмотрен на уроке Как вычислить площадь плоской фигуры? Интегралы от тангенса (котангенса) в четвертой и пятой степенях можно раздобыть на странице Сложные интегралы.

Как найти арксинус: формула, свойства, функция

Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).

Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу. В результате с помощью синуса можно, учитывая дугу окружности, определить хорду, которая ее стягивает.

Обратная функция под названием арксинус призвана решить противоположную задачу. Арксинус обозначают \(\arcsin x\) и определяют, как угол с синусом, равным х.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Для тригонометрических функций характерна периодичность. В связи с этим, обратные тригонометрические функции являются многозначными. Аркфункция обладает значением в виде множества из углов, для которых прямая тригонометрическая функция соответствует заданному числу.

Рассмотрим функцию: \(\arcsin ½\) . Данная аркфункция обозначает множество из углов:

(30^\circ, 150^\circ, 390^\circ, 510^\circ \dots) \right )\)

Значение синуса при этом: ½

Как правило, под обратными тригонометрическими функциями понимают ключевые значения каждой аркфункции, выделенные из ее множества значений.

Если \(-1\leqslant \alpha \leqslant 1\) , то любое решение уравнения \(\sin x=\alpha\) записывают в такой форме: \( x=(-1)^\arcsin \alpha +\pi n,

Арксинус числа х — значение для угла у, определенного в радианах, для которого \(\sin y=x,\quad —>\leqslant y\leqslant >,\quad |x|\leqslant 1\) .

Зачем нужен арксинус

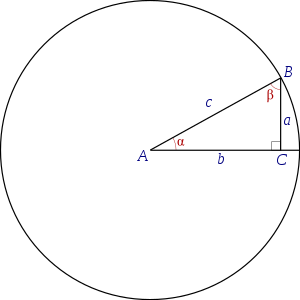
С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.

В том случае, когда имеется некий прямоугольный треугольник, обратные тригонометрические функции от отношений сторон позволяют определить угол. Например, длина катета составляет «а». Этот катет определяется, как противолежащий для угла \(\alpha\) , то:

\(\alpha =\arcsin(a/c)=\arccos(b/c)=\operatorname (a/b)=\operatorname (c/a)=\operatorname (c/b)=\operatorname (b/a)\)

Получение функции arcsin с пояснением на примерах

Предположим, что существует некая функция:

Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=\arcsin x нельзя причислить к функциям.

В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:

Функция \(y=\sin x \) на отрезке \(\left\) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой \(y=\arcsin x.\)

График обратной функции является симметричным графику функции \(y=\sin x\) в рамках интервала \(\left\) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.

Определим значение выражение:

По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.

Требуется найти, что означает \(\arcsin 0,5\) .

Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:

Общий ответ можно высчитать не в градусах, а в радианах:

Свойства функции arcsin

Рассмотрим функцию \(y=\arcsin x\) . Она является непрерывной в тригонометрии и ограничивается на протяжении всей своей области определения. Данная функция строго возрастает.

Формулы с обратными функциями тригонометрии

Уже были рассмотрены обратные тригонометрические функции. Они, как и другие функции имеют между собой связи и зависимости, которые можно выразить в виде формул и использовать для решения задач.

В данной работе мы рассмотрим основные формулы, в которых применяются функции тригонометрии. Разберём их виды, деление на группы, доказательства и способы решения задач с их помощью.

Группировка основных понятий

Сначала проведём группировку формул, для того чтобы сделать более понятной логику объяснений. И объединим все правила и доказательства в одну статью.

Синус от арксинуса для \

Тангенса от арктангенса для \.

Указанное в данных выражениях легко выводится из самих определений обратных функций тригонометрии. При необходимости найти arcsin tg, можно использовать приведённые формулы.

Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса

1. Исходим из t g α = sin α 1 — sin 2 α , — π 2 α π 2 . Получаем t g ( a r c sin α ) = sin ( a r c sin α ) 1 — sin 2 ( a r c sin α ) = α 1 — α 2 при условии, что — 1 α 1 .
2. Исходим из t g α = 1 — cos 2 α cos α , α ∈ , получаем

t g ( a r c cos α ) = 1 — cos 2 ( a r c cos α ) cos ( a r c c os α ) = 1 — α 2 α при условии α ∈ ( — 1 , 0 ) ∪ ( 0 , 1 ) .

1. Исходим из t g α = 1 c t g α , α ∈ ( 0 , π 2 ) ∪ ( π 2 , π ) , получаем t g ( a r c c t g α ) = 1 c t g ( a r c c t g α ) = 1 α при условии, что α ≠ 0 .

Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:

c t g α = 1 t g α

Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.

Неопределенный интеграл и его определение

Если функция является одной из первообразных для , то по определению .

• Здесь -знак интеграла,
• — подынтегральная функция,
• — переменная интегрирования,
• — постоянная интегрирования.

За переменную интегрирования можно принять любую переменную. Нахождение функции по производной называется интегрированием.

По определению найдите неопределенные интегралы.

Решение:

Так как:

Задача пример №2

Найдите интеграл .

Решение:

подумаем, производной какой функции является функция . Например, известно, что производной функции является функция . Значит, множителем искомой функции является дробь , которая потом сократиться с коэффициентом 4 и получится . Такой функцией является функция . Значит,

Разложение в ряды

• arcsin⁡x=x+x36+3×540+⋯ =∑n=∞(2n)!4n(n!)2(2n+1)x2n+1{\displaystyle \displaystyle \arcsin x=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots \ =\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}} для всех |x|≤1{\displaystyle \left|x\right|\leq 1}
• arccos⁡x=π2−arcsin⁡x=π2−∑n=∞(2n)!4n(n!)2(2n+1)x2n+1{\displaystyle \displaystyle \arccos x={\pi \over 2}-\arcsin x={\pi \over 2}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}} для всех |x|≤1{\displaystyle \left|x\right|\leq 1}
• arctg⁡ x=x−x33+x55−⋯ =∑n=1∞(−1)n−12n−1x2n−1{\displaystyle \displaystyle \operatorname {arctg} \ x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots \ =\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{2n-1}}x^{2n-1}} для всех |x|≤1{\displaystyle \left|x\right|\leq 1}

Основные формулы

1.	∫ 0·dx = C
2.	∫ a dx = ax + C      (a = const)
3.	∫ xn dx = xn+1n + 1 + C      (n ≠ -1)
4.	∫ dxx = ln |x| + C
5.	∫ ax dx = axln a + C
6.	∫ ex dx = ex + C
7.	∫ sin x dx = -cos x + C
8.	∫ cos x dx = sin x + C
9.	∫ dxsin2x = -ctg x + C
10.	∫ dxcos2x = tg x + C
11.	∫ dxa2 — x2 = arcsin xa + C = -arccos xa + C      (x < a)
12.	∫ dxa2 + x2 = 1a arctg xa + C = -1a arcctg xa + C
13.	∫ dxa2 — x2 = 12a ln x + ax — a + C      (|x| ≠ a) — «Высокий логарифм»
14.	∫ dxx2 ± a2 = ln |x + x2 ± a2|

Общие правила интегрирования функций

∫

cf(x) dx = c

∫

f(x) dx

∫

dx =

∫

f(x) dx +

∫

g(x) dx

∫

dx =

∫

f(x) dx —

∫

g(x) dx

∫

f(x)g(x) dx = f(x)

∫

g(x) dx —

∫∫

g(x) dxdf(x)

Интегралы от рациональных функций

1.	∫ xn dx = xn+1n + 1 + C      (n ≠ -1)
2.	∫ (ax + b)n dx = (ax + b)n+1a(n + 1) + C      (n ≠ -1)
3.	∫ dxx = ln |x| + C
4.	∫ dxax + b = 1a ln |ax + b| + C
5.	∫ ax + bcx + ddx = acx + bc — adc2 ln |cx + d| + C
6.	∫ dx(x + a)(x + b) = 1a — b ln |x + bx + a| + C
7.	∫ dxx2 — a2 = 12a ln |x — ax + a| + C
8.	∫ x dx(x + a)(x + b) = 1a — b (a ln |x + a| — b ln|x + b|) + C
9.	∫ x dxx2 — a2 = 12 ln |x2 — a2| + C
10.	∫ dxx2 + a2 = 1a arctg (xa) + C
11.	∫ x dxx2 + a2 = 12 ln |x2 + a2| + C
12.	∫ dx(x2 + a2)2 = 12a2xx2 + a2 + 12a3 arctg (xa) + C
13.	∫ x dx(x2 + a2)2 = -121×2 + a2 + C
14.	∫ x dx(x2 + a2)3 = -141(x2 + a2)2 + C
15.	∫ dxax2 + bx + c = 1b2 — 4ac ln2ax + b — b2 — 4ac2ax + b + b2 — 4ac + C     (b2 — 4ac > 0)
16.	∫ dxax2 + bx + c = 14ac — b2 arctg2ax + b4ac — b2 + C     (b2 — 4ac < 0)
17.	∫ x dxax2 + bx + c = 12a ln|ax2 + bx + c| — b2a ∫ dxax2 + bx + c
18.	∫ x dxax + b = 1a2(ax + b — b ln |ax + b|) + C
19.	∫ x2dxax + b = 1a3(12(ax + b)2 -2b(ax + b) + b2 ln |ax + b|) + C
20.	∫ dxx(ax + b) = 1b ln ax + bx + C
21.	∫ dxx2(ax + b) = — 1bx + ab2 ln ax + bx + C
22.	∫ x dx(ax + b)2 = 1a2(ln |ax + b | + bax + b) + C
23.	∫ x2dx(ax + b)2 = 1a3(ax + b — 2b ln |ax + b | — b2ax + b) + C

Интегралы от трансцендентных функций

1.	∫ ex dx = ex + C
2.	∫ ax dx = axln a + C
3.	∫ dxx ln x = ln |ln x| + C
4.	∫ xn ln xdx = xn + 1(ln xn + 1 — 1(n + 1)2) + C
5.	∫ eax ln xdx = eax ln xa — 1a ∫ eaxxdx
6.	∫ xn lnmxdx = xn + 1n + 1 lnmx — mn + 1 ∫ xn lnm — 1xdx
7.	∫ xnlnmxdx = -xn + 1(m — 1) lnm — 1x + n + 1m — 1 ∫ xnlnm — 1xdx
8.	∫ ln x dx = x ln x — x + C
9.	∫ arcsin x dx = x arcsin x + 1 — x2 + C
10.	∫ arctg x dx = x arctg x — ln 1 + x2 + C
11.	∫ eax dx = eaxa + C
12.	∫ x eax dx = eaxa2(ax — 1) + C
13.	∫ axxn dx = ax(n — 1)xn — 1 + ln an — 1 ∫ axxn — 1
14.	∫ sh(x) dx = ch(x) + C
15.	∫ ch(x) dx = sh(x) + C

Интегралы от иррациональных функций

1.	∫ dxax + b = 2aax + b + C
2.	∫ ax + bdx = 23a(ax + b)1.5 + C
3.	∫ x dxax + b = 2(ax — 2b)3a2ax + b + C
4.	∫ xax + bdx = 2(3ax — 2b)15a2(ax + b)1.5 + C
5.	∫ dx(x + c)ax + b = 1b — ac lnax + b — b — acax + b + b — ac + C     (b — ac > 0)
6.	∫ dx(x + c)ax + b = 1ac — b arctgax + bac — b + C     (b — ac < 0)
7.	∫ ax + bcx + ddx = 1c(ax + b)(cx + d) — ad — bccac arctg a(cx + d)c(ax + b) + C
8.	∫ dxxax + b = 1b lnax + b — bax + b + b + C     (b > 0)
9.	∫ dxxax + b = 1-b arctgax + b-b + C     (b < 0)
10.	∫ dxx2ax + b = -ax + bbx — a2b ∫ dxxax + b
11.	∫ ax + bxdx = 2ax + b + b ∫ dxxax + b
12.	∫ a — xb + xdx = (a — x)(b + x) + (a + b)arcsinx + ba — x + C
13.	∫ a + xb — xdx = -(a + x)(b — x) — (a + b)arcsinb — xa + x + C
14.	∫ dxax2 + bx + c = 1a ln|2ax + b + a(ax2 + bx + c)| + C
15.	∫ dxax2 + bx + c = -1a arcsin2ax + bb2 — 4ac + C
16.	∫ ax2 + bx + cdx = 2ax + b4aax2 + bx + c + 4ac — b28a ∫ dxax2 + bx + c
17.	∫ x2 + a2dx = x2x2 + a2 + a22 ln |x + x2 + a2| + C
18.	∫ x2 — a2dx = x2x2 — a2 — a22 ln |x + x2 — a2| + C
19.	∫ dxx2 + a2 = ln|x + x2 + a2)| + C
20.	∫ dxx2 — a2 = ln|x + x2 — a2)| + C
21.	∫ x dxx2 + a2 = x2 + a2 + C
22.	∫ x2 — a2xdx = x2 — a2 + a arcsin (xa) + C
23.	∫ a2 — x2dx = x2a2 — x2 + a22 arcsin (xa) + C
24.	∫ a2 — x2xdx = a2 — x2 + a ln (xa + a2 — x2) + C
25.	∫ dxa2 — x2 = arcsin (xa) + C
26.	∫ x dxa2 — x2 = -a2 — x2 + C
27.	∫ dxxa2 — x2 = 1a ln |xa + a2 — x2| + C

Интегралы от тригонометрических функций

1.	∫ sin (x) dx = -cos (x) + C
2.	∫ cos (x) dx = sin (x) + C
3.	∫ sin2 (x) dx = x2 — 14 sin (2x) + C
4.	∫ cos2 (x) dx = x2 + 14 sin (2x) + C
5.	∫ sinn (x) dx = -1n sinn — 1 (x) cos (x) + n — 1n ∫ sinn — 2 (x) dx
6.	∫ cosn (x) dx = 1n cosn — 1 (x) sin (x) + n — 1n ∫ cosn — 2 (x) dx
7.	∫ dxsin (x) = ln|tg(x2)| + C
8.	∫ dxcos (x) = ln|ctg(x2)| + C
9.	∫ dxsin2 (x) = -ctg (x) + C
10.	∫ dxcos2 (x) = tg (x) + C
11.	∫ sin (x) cos (x) dx = -14cos (2x) + C
12.	∫ sin2 (x) cos (x) dx = 13sin3 (x) + C
13.	∫ sin (x) cos2 (x) dx = -13cos3 (x) + C
14.	∫ sin2 (x) cos2 (x) dx = -18x — 132sin (4x) + C
15.	∫ tg (x) dx = -ln |cos (x)| + C
16.	∫ ctg (x) dx = ln |sin (x)| + C
17.	∫ sin (x)cos2 (x)dx = 1cos (x) + C
18.	∫ cos (x)sin2 (x)dx = -1sin (x) + C
19.	∫ sin2 (x)cos2 (x)dx = tg (x) — x + C
20.	∫ cos2 (x)sin2 (x)dx = -ctg (x) — x + C
21.	∫ sin2 (x)cos (x)dx = ln|ctg(x2)| — sin (x) + C
22.	∫ cos2 (x)sin (x)dx = ln|tg(x2)| + cos (x) + C
23.	∫ dxsin (x) cos (x) = ln|tg(x)| + C
24.	∫ dxsin2 (x) cos (x) = -1sin (x) + ln|ctg(x2)| + C
25.	∫ dxsin (x) cos2 (x) = 1cos (x) + ln|tg(x2)| + C
26.	∫ dxsin2 (x) cos2 (x) = tg(x) — ctg(x) + C
27.	∫ dxsinn (x) = -1n — 1cos (x)sinn — 1 (x) + n — 2n — 1 ∫ dxsinn — 2 (x)
28.	∫ tgn (x) dx = tgn — 1 (x)n — 1 — ∫ tgn — 2 (x) dx
29.	∫ ctgn (x) dx = -ctgn — 1 (x)n — 1 — ∫ ctgn — 2 (x) dx
30.	∫ sin (x) cosn (x) dx = -cosn + 1 (x)n + 1 + C
31.	∫ cos (x) sinn (x) dx = sinn + 1 (x)n + 1 + C

Примеры

Найти следующие интегралы и сделать проверку.

1) ∫(2x – 3) dx. Используем свойства V и IV, формулы 1). и 3).

(Наш лист Интегралы)

∫(2x – 3) dx = 2∫xdx — 3∫dx = 2·x²/2  – 3x + C = х2 – 3х + С.

Проверка.   F'(x) = (х2 – 3х + С)’ = 2x – 3 = f (x).

2). ∫(2x – 3)2dx.  Преобразуем подынтегральную функцию по формуле ФСУ (формулы сокращенного умножения): (a – b)2 = a2 – 2ab + b2, а затем используем те же свойства и формулы, что и в примере 1).

∫(2x – 3)2dx =∫( 4×2 – 12x + 9) dx = 4∫x2dx — 12∫xdx + 9∫dx =

= 4·x³/3 — 12· x²/2 + 9x + C = ( 4/3) x3 – 6×2 + 9x + C.

Проверка.   F'(x) = ((4/3) x3 – 6×2 + 9x + C)’ =(4/3)  · 3×2 — 6·2x + 9 = 4×2 – 12x + 9 = (2x – 3)2 = f (x).

Решим пример 2) вторым способом — подведения под знак дифференциала.

Итак, требуется найти  ∫(2x – 3)2dx.

Будем использовать формулу 1). Вместо u у нас (2х – 3) и, по формуле 1), переменная интегрирования должна быть такой же, как и основание степени, т. е (2х – 3). Хорошо,  вместо dx запишем d(2x – 3). И что изменилось? d (2x – 3) = 2dx, т.е. подынтегральное выражение стало больше в 2 раза. Разделим его на 2. Для этого перед значком интеграла поставим множитель ½.

Значит,∫(2x – 3)2dx = (½)∫( 2x – 3)2 d (2x – 3).     Мысленно представляйте себе u2 вместо

(2х – 3)2  и du вместо d(2x – 3). Увидели ∫u2du ?  И что получится? Верно:  u³/3+ C.

«Долго сказка сказывается…», а решаются такие примеры быстро:

∫(2x – 3)2dx =  (½)∫(2x – 3)2 d (2x – 3) =(½) ·(2x-3)³/3  + С =(1/6) · (2х – 3)3 + С.

Проверка.   (F (x)+С)′ = ( 1/6· (2х – 3)3 + С)’ =  (1/6)· 3 (2x – 3)2 · 2 = (2x – 3)2 = f (x).

Сравните эти два способа решения примера 2. Что, не впечатлил второй способ? Тогда пример 3).

3) ∫(2x – 3)7dx.   Желаете возводить (2х – 3) в седьмую степень? А-а, то-то же!

Решаем способом подведения под знак дифференциала, т.е. вторым способом так же, как предыдущий пример.

∫(2x – 3)7dx =  (½)∫(2x – 3)7d (2x – 3) =  (½)· (2x – 3)8 /8 + C =(1/16) (2x – 3)8 + C.

Проверка. F'(x) = ((1/16)(2x – 3)8 + C)’ =(1/16) ·8 (2x – 3)7·2 = (2x – 3)7 = f (x).

Синус от арккосинуса, тангенс от арксинуса и иже с ними

На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.

Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид , таким образом .

Другой пример: используя формулу синуса арккосинуса вида , мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем . Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).

Осталось показать вывод записанных формул.

Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.

Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств и , а также учитывая, что , легко получить следующие формулы , и , выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.

Вот краткая запись вышеперечисленных выкладок:

• так как , то ;
• так как , то ;
• так как , то .

По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:

• так как , то ;
• так как , то ;
• так как , то .

Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:

• так как , то при ;
• так как , то при ;
• так как , то при .

Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как .

Синус от арккосинуса, тангенс от арксинуса и иже с ними

На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.

Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид , таким образом .

Другой пример: используя формулу синуса арккосинуса вида , мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем . Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).

Осталось показать вывод записанных формул.

Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.

Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств и , а также учитывая, что , легко получить следующие формулы , и , выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.

Вот краткая запись вышеперечисленных выкладок:

• так как , то ;
• так как , то ;
• так как , то .

По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:

• так как , то ;
• так как , то ;
• так как , то .

Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:

• так как , то при ;
• так как , то при ;
• так как , то при .

Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как .