Уравнение сферы
В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.
Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.
Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х, у, z), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:
Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству
то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.
Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.
Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:
Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).
Решение. Сначала составляем уравнение сферы, описанной в условии:
Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.
Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:
Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?
Решение. Обозначим вершины треугольника точками А, В и С. Пусть
Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?
Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:
Шар
Шар и сфера – это аналог круга и окружности в плоскости. Шар представляет собой фигуру, полученную вращением полукруга вокруг одной точки.
Шар имеет площадь поверхности: $S=4pir^2$
Радиус это отрезок, соединяющий центр шара и любую из точек на его поверхности.
Формула объема шара$V={4pir^3\over3}$
Объем показывает, какое пространство занимает фигура. Чтобы понять, что такое объем нужно представить себе фигуру полой. Тогда объем это количество воды, которое можно налить в эту фигуру
Шар, как и любую другую трехмерную фигуру, можно рассечь плоскостью. Секущей плоскостью шара является круг, центр которого можно найти, опустив из центра шара перпендикуляр на окружность.
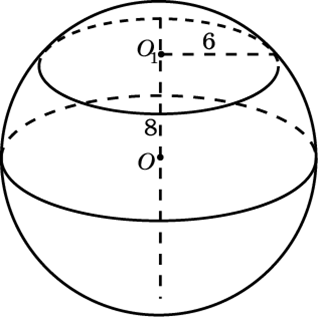
Рис. 2. Сечение шара.
Сфера это фигура, представляющая собой множество точек в пространстве, равноудаленных от центра сферы. Сфера:
- Имеет те же формулы объема и площади поверхности, что и шар.
- Секущая плоскость сферы это окружность
- Центр секущей окружности, находится так же, как и в случае с шаром
Рис. 3. Сфера.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение.Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула.Площадь внешней поверхности сегмента сферы с высотой h
через радиус сферы R:
S = 2π
Rh
Мы даем здесь очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).
Тогда, обозначая через площадь этого участка — основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):
Если теперь всю поверхность шара разложить на очень большое число N таких малых областей , тем самым объем шара на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой
где последняя сумма равна полной поверхности шара:
Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу
Последний результат формулируется так:
Площадь поверхности шара равна учетверенной площади его большого круга.
Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. сферическую поверхность, или «шапочки»; см. рис. 409). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:
откуда находим для площади шапочки формулу
Шаровым поясом (см. рис. 408) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек:
где — высота слоя. Итак, площадь поверхности шарового пояса для данного шара зависит только от высоты соответствующего слоя, но не от его положения на шаре.
Задача. Боковая поверхность конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара. Найти высоту конуса, если радиус шара равен .
Решение. Введем для удобства угол а между высотой и образующей конуса (рис. 413). Найдем для высоты, радиуса основания и образующей конуса выражения
Определение шара
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее R R
R
— радиус этого шара.
Примеры решения задач
Задача 1
Геометрическое тело шарообразной формы обладает объемом, равным \(\frac{36}{\sqrt\pi}\). Необходимо вычислить значение поверхностной площади объекта при условии увеличения его радиуса на величину \(\frac{6}{\sqrt\pi}\).
Решение
При известном радиусе и объеме шара достаточно просто определить значение поверхностной площади заданной фигуры. С этой целью нужно вспомнить соответствующие формулы из курса теории. Применим эти уравнения к условиям задачи и выполним необходимые вычисления:
\(V_{\text{шара}} = \frac{4}{3}\pi R^3 = \frac{36}{\sqrt\pi} \Rightarrow R = \frac{3}{\sqrt\pi}\)
Найдем радиус полученного шара:
\(R_{\text{нов.}} = R + \frac{6}{\sqrt\pi} = \frac{9}{\sqrt\pi}\)
Далее остается лишь путем подстановки найденных значений в стандартную формулу определить искомую площадь поверхности:
\(S_{\text{пов.}} = 4\pi R_{\text{нов.}}^2 = 4\pi \left(\frac{9}{\sqrt\pi}\right)^2 = 4\pi\frac{81}{\pi} = 324\)
Ответ: \(S_{\text{пов.}} = 324\)
Задача 2
Дана шарообразная фигура. Необходимо вычислить, в какое количество раз объем этого объекта превышает аналогичные параметры фрагмента с высотой, равной половине радиуса.
Решение
В процессе решения задачи потребуется найти частное от деления объема шара на объем обозначенного в условии сегмента. Высоту рассматриваемого фрагмента допустимо выразить с помощью следующего уравнения:
\(H = \frac{1}{2}R\)
Далее воспользуется стандартными формулами, знакомыми из теоретического курса стереометрии, и выполним соответствующие расчеты:
\(\frac{V_{\text{шара}}}{V_{\text{сегм.}}} = \frac{\frac{4}{3}\pi R^3}{\pi \left(\frac{1}{2}R\right)^2\left(R — \frac{1}{3}\left(\frac{1}{2}R\right)\right)} = \frac{\frac{4}{3}\pi R^3}{\frac{5}{24}\pi R^3} = \frac{4}{3} \cdot \frac{24}{5} = \frac{32}{5} = 6,4\)
Ответ: 6,4
Задача 3
На рисунке ниже изображена пара сфер, отличающихся по размеру. Радиус первой фигуры в два раза превышает аналогичные параметры второго объекта. Вторая сфера целиком погружена в пространство, ограниченное первой сферической фигурой. При условии, что объем шара, который расположен внутри второй сферы составляет \(V_2\), объем объекта, расположенного между сферами соответствует V. Требуется вычислить соотношение \(V : V_2\).

Решение
Представим, что \(V_1\) представляет собой объем шарообразной фигуры, которая ограничена первой сферой. Исходя из того, что радиус \(S_1\) в два раза превышает значение радиуса \(S_2\), целесообразно записать следующее соотношение:
\(V_1 : V_2 = 8\)
Таким образом:
\(V = V_1 — V_2 = 8V_2 — V_2 = 7V_2\)
В результате получим:
\(V : V_2 = 7\)
Части шара
Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом. На рисунке ниже окрашен в зеленый цвет.
Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем. На рисунке ниже закрашен желтым.
Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента. На рисунке ниже сектор залит оранжевым.
Секущая, хорда, секущая плоскость сферы и их свойства
Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Секущая плоскость — это плоскость, которая пересекает сферу.
Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).Любая хорда, проходящая через центр сферы (шара) является диаметром.Хорда является отрезком секущей прямой.Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 — m2,
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.Определение.Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновенияРасстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.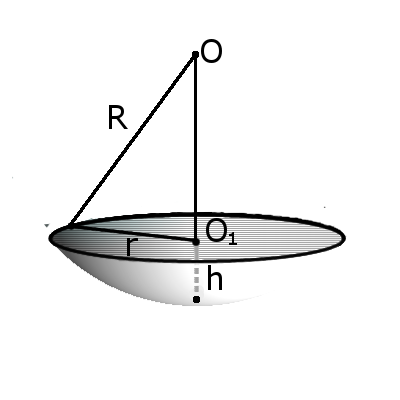
Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегментаh называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула.Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула.Объём сегмента сферы с высотой h через радиус сферы R:
| V = | h2π | (3R — h) |
| 3 |

Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.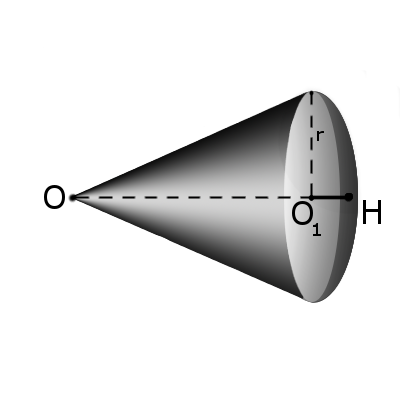
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR — h2)
Объём сектора V с высотой O1H (h) через радиус шара OH (R):
| V = | 2πR2h |
| 3 |
Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
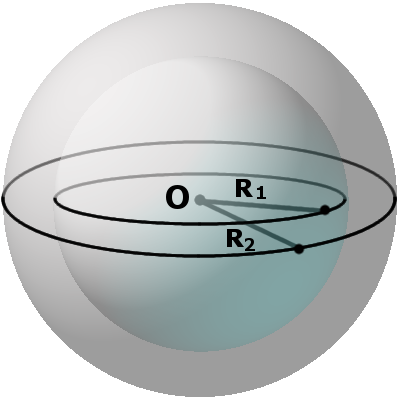
Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
Определение шара и сферы
Шар — это совокупность всех точек трехмерного пространства, находящихся на заданном расстоянии от точки, называемой центром шара (точка O на рисунке ниже). Другими словами, это набор точек, ограниченных сферой.
Сфера образована вращением окружности вокруг своего диаметра (оси) на 180° или полуокружности на 360°.
Сфера – это поверхность сферы. Он образован вращением круга вокруг его диаметра на 180° или полукруга на 360°.
Есть два типа мячей:
- закрытый — включает пулю;
- открытый — исключает сферу.
Радиус сферы (сферы) – это расстояние между центром и точками, расположенными на поверхности. На рисунке выше он отмечен буквой R.
Диаметр сферы (сферы) – это отрезок, проходящий через центр шара и соединяющий две противоположные точки на поверхности. Совпадает с осью шара, обычно обозначаемой буквой d.
Полюса шара (шара) – это точки А и В, расположенные на концах его диаметра.
Шар
Шар и сфера — аналог круга и круга на плоскости. Шар – это фигура, полученная вращением полуокружности вокруг точки.
Шар имеет площадь поверхности: $S=4pir^2$
Радиус — это отрезок, соединяющий центр шара и некоторые точки на поверхности.
Формула объема шара$V={4pir^3over3}$
Объем показывает, сколько места занимает фигура. Чтобы понять, что такое объем, нужно представить себе полую фигуру. Тогда объем — это количество воды, которое можно налить в эту фигуру
Шар, как и любую другую трехмерную фигуру, можно разрезать плоскостью. Секущая плоскость шара представляет собой окружность, центр которой можно найти, опустив перпендикуляр из центра шара на окружность.
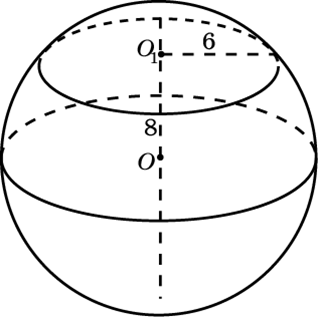
Рис. 2. Разрез мяча.
Хотя в школьном курсе таких ситуаций не бывает, но надо понимать, что мяч можно разрезать плоскостью под углом. Но и в этом примере секущая плоскость останется шаром.
Сфера
Сфера — это фигура, представляющая собой множество точек в пространстве, равноудаленных от центра сферы. Сфера:
- Он имеет те же формулы объема и площади поверхности, что и сфера.
- Секущая плоскость сферы представляет собой окружность
- Центр секущей окружности находится так же, как и для шара
Рис. 3. Круто.
В чем различие
Тогда возникает вопрос, чем отличается мяч от пули, кроме определения? Дело в том, что различия между сферой и сферой гораздо более размыты, чем различия между кругом и кругом. Сфера также имеет объем и площадь поверхности.
Возможно, кроме определения, отличие заключается в том, что в задачах никогда не встречается объем сферы. Как правило, ищут объем мяча. Это не означает, что сфера не имеет объема. Это объемная фигура, поэтому она имеет объем.
Аналогия просто проводится с кругом, у которого нет площади. Это не правило, а скорее традиция, которую необходимо помнить: в геометрии не приветствуется формулировка объема сферы.
Еще одно отличие, которое можно считать более или менее существенным: секущая плоскость сферы: круг, не имеющий внутреннего пространства, но имеющий длину. Плоскость сечения сферы: круг, имеющий площадь и не имеющий окружности. Поэтому стоит быть внимательным в формулировке задачи, чтобы не было ошибок из-за таких мелочей.
Правило встречается в следующих упражнениях:
7 класс
Задание 1224, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1227, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1228, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 23, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 24, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 25, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 26, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1253, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1254, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
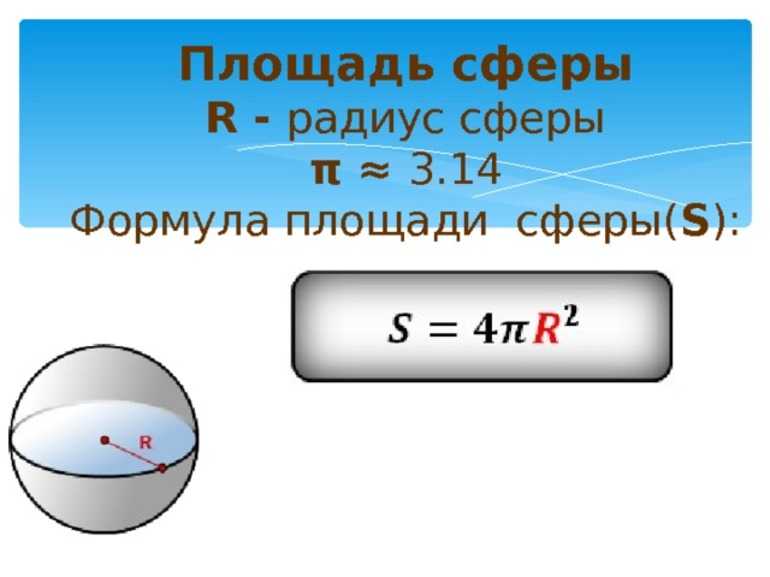
- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Формулы площади и объема с доказательством
Как и в случае любых геометрических форм, для сферы и шара предусмотрены формулы, с помощью которых можно вычислить их параметры. Подобные математические соотношения полезны при решении задач по стереометрии. Зная величину радиуса или диаметра объекта, несложно рассчитать его площадь и объем. Рассмотрим такие выражения и докажем, что они являются справедливыми равенствами.
\(S=\ 4\pi r^{2}\)
\(S=\ \pi d^{2}\)
\(V={\frac {4}{3}}\pi r^{3}\)
Необходимо подтвердить корректность записанных равенств. С этой целью следует выделить одну четвертую часть от круга, радиус которого равен R, а его центральная точка совпадает с точкой, имеющей координаты \(\left(0;0\right)\). Запишем уравнение окружности, применимое для рассматриваемого случая:
\(x^{2}+y^{2}=R^{2}\)
В результате получим, что:
\(y^{2}=R^{2}-x^{2}\)
Заметим, что функция \(y={\sqrt {R^{2}-x^{2}}},x\in (0;R)\) не прерывается, убывает и не является отрицательной. В процессе вращательного движения четвертая часть круга относительно оси абсцисс формирует некий полушар. Исходя из этого, допустимо составить следующее равенство:
\({1 \over 2}V=\pi \int \limits _{0}^{R}(R^{2}-x^{2})dx=\pi \cdot {\Bigl .}\left(R^{2}x-{\frac {x^{3}}{3}}\right){\Bigr |}_{0}^{R}=\pi \cdot (R^{3}-{\frac {R^{3}}{3}})={\frac {2}{3}}\pi R^{3}\)
Таким образом, получим исходное соотношение:
\(V={\frac {4}{3}}\pi R^{3}\)
Путем нескольких несложных математических преобразований удалось доказать справедливость записанных формул. Далее также в некоторое количество действий допустимо подтвердить справедливость следующего выражения:
\(V={\frac {\pi d^{3}}{6}}\)
Доказательство:
\(d=2r, V={4 \over 3} \pi r^3 = {4 \over 3} \pi \left ( {d \over 2} \right )^3 = {4 \over 3} \pi \frac {d^3} {8} = \frac {\pi d^3} {6}\)
Касательная плоскость к сфере
Плос-ть, имеющая со сферой строго одну общую точку, именуется касательной плоскостью к сфере.
Действительно, если плос-ть касается окруж-ти, то точка касания А должна располагаться на расстоянии R от центра сферы О, где R– радиус сферы. Все остальные точки касательной плос-ти находятся вне пределов сферы, то есть должны находиться от О на расстоянии, превышающем R. Это значит, что отрезок ОА должен быть кратчайшим отрезком, соединяющим О и касательную плос-ть. Но мы знаем, что кратчайший отрезок между плос-тью и точкой – это как раз перпендикуляр, опущенный из точки на плос-ть.
Справедливо и обратное утверждение:
Доказательство. Если радиус ОА – перпендикуляр к плос-ти α, то он является кратчайшим расстоянием между плос-тью и центром О. Тогда все остальные точки плос-ти располагаются на большем расстоянии от О, чем точка А. Это значит, что они не располагаются на сфере. Значит, у сферы и плос-ти α одна общая точка А, а потому α по определению – касательная плос-ть.
По аналогии с касательной плос-тью существует понятие касательной прямой к сфере.
Касательная к сфере обладает почти теми же свойствами, что и касательная к окруж-ти.
Доказательство. Пусть m– касательная прямая к сфере с центром О. обозначим точку касания как А. Далее через прямую m и центр О проведем плос-ть α. Нам надо показать, что ОА⊥m:
Плос-ть α будет диаметральной плос-тью. Сечение будет иметь форму окруж-ти с центром О и радиусом ОА. Прямая m будет касательной к этой окруж-ти, ведь она имеет с ней общую точку А, а второй общей точки m и окруж-ть иметь не могут, ведь такая бы точка была бы также общей для m и сферы, а m по определению имеет лишь одну общую точку со сферой. Напомним, что касательная к окруж-ти перпендикулярна радиусу, то есть m⊥ОА, ч. т. д.
Будет верным и обратное утверждение:
Для доказательства используем ту же картинку. Известно, что m⊥ОА, надо показать, что m– касательная к сфере. Проведем через пересекающиеся прямые m и ОА плос-ть α. Она снова окажется диаметральной плоскостью, и снова сечением будут окруж-ть с радиусом ОА. По признаку касательной, который мы изучали в планиметрии, m– касательная к этой окруж-ти, ведь m⊥ОА. То есть в плос-ти α есть лишь одна общая точка m и сферы. В других плос-тях у них не может быть общих точек, так как m полностью принадлежит α. В итоге у m и сферы только одна общая точка, а потому m– касательная к сфере, ч. т. д.
Рассмотрим ещё одно утверждение:
Сначала разберемся с понятием отрезков касательных. Пусть из точки А, лежащей вне сферы, к ней проведены две касательные, а точки касания обозначены буквами В и С. Тогда АВ и АС как раз и будут отрезками касательных:
Докажем, что эти отрезки одинаковы. Для этого к точкам касания проведем радиусы ОВ и ОС. Теперь сравним ∆АВО и ∆АСО. Они прямоугольные, ведь ОВ⊥АВ по свойству касательной, и ОС⊥АС. Гипотенуза АО у этих треугольников общая, а катеты ОВ и ОС – это одинаковые радиусы. Получается, что ∆АВО и ∆АСО равны, а потому отрезки АВ и АС одинаковы.
Задание. Дан шар радиусом 10 см, к которому проведена касательная плос-ть α. Через точку касания проведена секущая плос-ть β, образующая с α угол в 30°. Вычислите площадь сечения шара плос-тью β.
Решение. Обозначим точку касания как А. Опустим из центра сферы о перпендикуляр ОН на плос-ть β. Тогда отрезок АН будет радиусом сечения. Так как угол между плос-тями α и β составляет 30° (на рисунке он показан как ∠НАС), то
Ответ: 25π см2.
Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.
Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:
Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?
Решение. Обозначим вершины треугольника точками А, В и С. Пусть
AB = 13
AC = 14
BC = 15
Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?
Напомним одну из формул для расчета площади треугольника:
Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:
Касательная, касательная плоскость к сфере и их свойства
Определение Касательной к сфере называется прямая, которая касается сферы только в одной точке. Определение. Касательная плоскость к сфере — это плоскость, которая касается сферы только в одной точке. Касательная линия (плоскость) всегда перпендикулярна радиусу сферы, проведенной к точке касания. Расстояние от центра сферы до касательной (плоскости) равно радиусу сферы.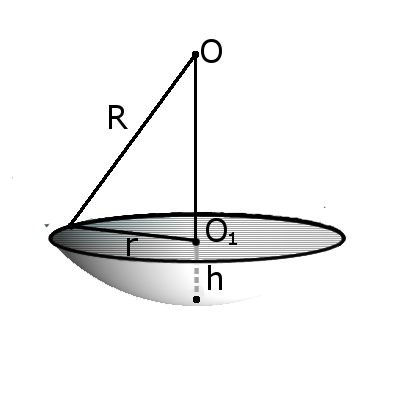
Определение: Сегмент шара — это часть шара, отсеченная от шара секущей плоскостью. Основанием сегмента называется круг, который образовался на месте разреза. Высота отрезка h — это длина перпендикуляра, проведенного из центра основания отрезка к поверхности отрезка. Формула. Площадь внешней поверхности сегмента сферы высотой h через радиус сферы R:
S = 2πRh
Формула. Объем сегмента сферы высотой hi равен радиусу сферы R:
| В = | h2π | (3R-ч) |
| 3 |

Определение: Диск шара – это часть шара, образованная в результате его сечения двумя параллельными плоскостями и расположенная между ними.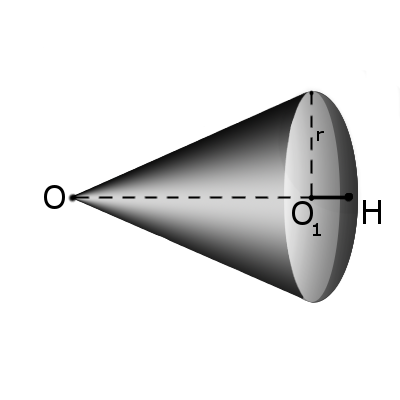
Определение. Сектором называется часть шара, ограниченная суммой всех лучей, исходящих из центра шара О и образующих на поверхности окружность радиусом г. Формула. Площадь поверхности сектора S высотой O1H (h) через радиус сферы OH (R):
S = πR(2t + √2tR — h2)
Формула Объем сектора V высотой O1H (h) через радиус сферы OH (R):
| В = | 2πR2h |
| 3 |
Определение: Касательные сферы (сферы) – это любые две сферы (сферы), имеющие общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.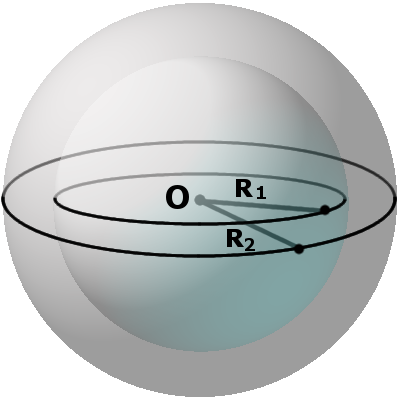
Определение: концентрическими сферами называются любые две сферы, имеющие общий центр и радиусы разной длины. Формулы геометрии
Основные свойства объемных фигур
Объемные фигуры – это фигуры, которые имеют не только длину и ширину, но и высоту. Они занимают некоторое пространство в трехмерном пространстве и могут иметь различные формы и размеры
Важно понимать основные свойства и характеристики объемных фигур для правильного их изучения и использования в задачах геометрии, физики, строительства и других областях
1. Объем
Объем фигуры – это мера ее трехмерного пространства, которое она занимает. Объем измеряется в таких единицах, как кубические метры (м³), кубические сантиметры (см³) и другие. Определение объема различных объемных фигур требует знания их основных параметров, например, длины, ширины, высоты или радиуса.
2. Площадь поверхности
Площадь поверхности фигуры – это мера площади всех ее боковых поверхностей. В отличие от площади плоской фигуры, площади поверхностей объемных фигур не могут быть просто вычислены как произведение двух сторон. Для каждой фигуры необходимо знать соответствующую формулу или алгоритм для вычисления площади поверхности.
3. Периметр основания
Периметр основания фигуры – это сумма длин всех сторон ее основания. Периметр обычно измеряется в единицах длины, например, в метрах или сантиметрах. Периметр основания может быть важным параметром для определения объема и площади поверхности некоторых объемных фигур.
4. Вершины и ребра
Вершины – это точки пересечения ребер объемной фигуры. Ребра – это отрезки, соединяющие вершины фигуры. Количество вершин и ребер в фигуре зависит от ее формы и может значительно варьироваться.
5. Виды объемных фигур
Существует множество различных видов объемных фигур, таких как куб, параллелепипед, сфера, цилиндр, конус и многие другие. Каждая фигура имеет свои особенности и характеристики, которые определяются ее формой и размерами. Знание основных свойств каждого вида объемных фигур позволяет более эффективно работать с ними и решать соответствующие задачи.
Примеры объемных фигур
Куб
Параллелепипед
Сфера






























