Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Интересные факты из области математики
Будет ли для вас новостью узнать, что за расшифровку секретной переписки правительства Испании, Франсуа Виета хотели отправить на костер, так как считали, что узнать шифр мог только дьявол, а человеку это не по силам.
Известно ли вам, что первым человеком, который предложил нумеровать кресла, ряды и места, был Рене Декарт? Аристократы-театралы даже просили короля Франции дать за это Декарту награду, но, увы, король отказал, так как считал, что давать награды философу – это ниже его достоинства.
Из-за учащихся, которые могли запомнить теорему Пифагора, но не смогли ее понять, эту теорему называли «ослиным мостом». Это значило, что ученик «осел», который не смог преодолеть мост. В данном случае мостом считали теорему Пифагора.
Писатели сказочники посвящали свои произведения не только мифическим героям, людям и зверюшкам, но и математическим символам. Так, например, автор знаменитой «Красной Шапочки», написал сказку о любви циркуля и линейки.
Срединный треугольник
Это особый вид фигуры с тремя вершинами, который строится на средних линиях. Поскольку любой треугольник имеет всего три линии указанного вида, то вместе они образуют новую фигуру, вершины которой расположены на серединах сторон исходной.

Построенный геометрический объект делит исходную фигуру на четыре одинаковые части. Доказать это можно следующим образом: если начертить срединный треугольник и обозначить черточками все его стороны, а также длины сторон исходного геометрического объекта, то можно увидеть, что сам он, а также три других фигуры при вершинах исходной имеют по три одинаковых стороны. Иными словами, выполняется признак их подобия. Равенство сторон всех четырех фигур говорит об одинаковом значении их площадей.
Еще одним интересным свойством срединной фигуры является возможность построения внутри нее точно такого же геометрического объекта. Он также будет подобен исходному треугольнику, но уже будет иметь в 8 раз меньшую площадь. Если продолжать такие геометрические построения, то площади срединных треугольников будут становиться все меньше, а пространство на плоскости, которое они будут покрывать, стремится к гравитационному центру исходной фигуры.
Таким образом, формула длины средней линии получается исходя из признака подобия треугольников по углу и двум прилежащим сторонам. Она всегда составляет половину от противоположной стороны. При выполнении геометрического построения срединного треугольника образуются четыре новых фигуры, которые подобны исходной. Гравитационные центры первоначального геометрического объекта и срединной фигуры совпадают.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
Доказательство.
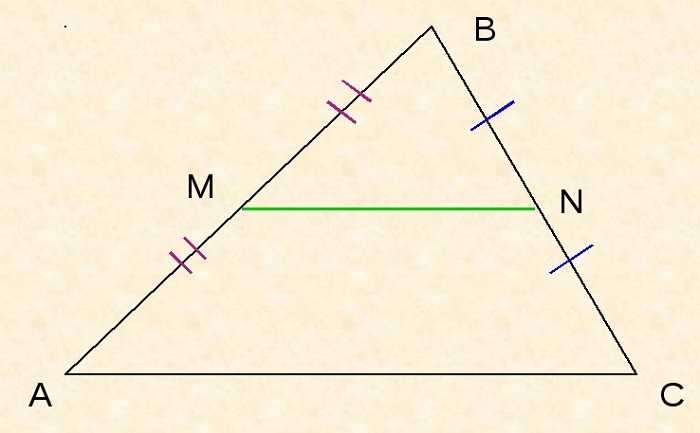
По определению стороны AB и BC делятся пополам, поэтому
Согласно теореме,
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
Доказано.
Следствие №2
Доказательство.
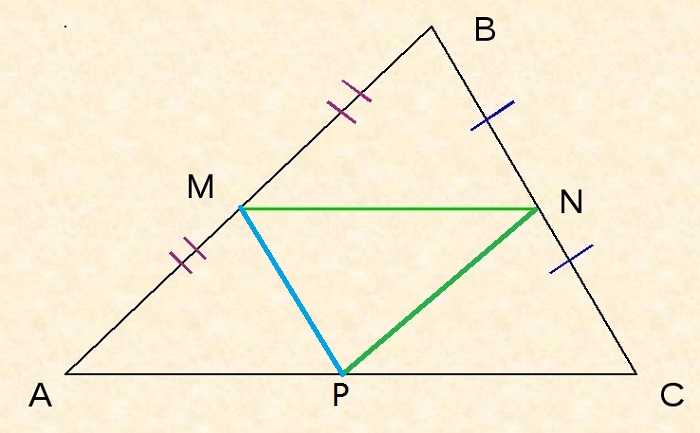
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Доказано.
Как вычислить, основные формулы
Через основания
Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Через основание, высоту и углы при нижнем основании
Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия, \(h\) – высота, \(\alpha,\beta\) – углы при нижнем основании.
Через диагонали, высоту и угол между диагоналями
Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия, \(h\) – высота, \(\alpha,\beta\) – углы между диагоналями, \(d_1\) , \(d_2\) – диагонали трапеции.
Средняя линия четырёхугольника
Средняя линия четырёхугольника
— отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства
Первая линия соединяет 2 противоположные стороны.
Вторая соединяет 2 другие противоположные стороны.
Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма . Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона ;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода
. Средние линии второго рода
— четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода
выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона . - Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.

Доказательства
Первый способ
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
Пусть NP II AB.
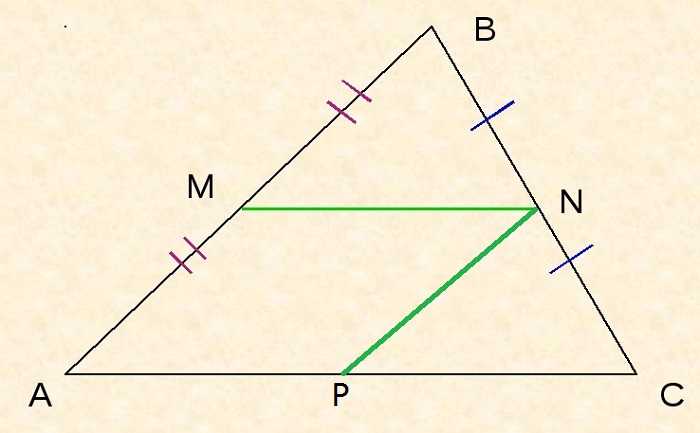
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Доказано.
Второй способ
Рассматриваются треугольники MBN и ABC. В них угол B является общим.
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Доказано.
Третий способ
Рассматривается сумма векторов
Поскольку в результате образуется замкнутая ломаная, то
Отсюда следует, что
Так как
![]()
то
![]()
Из последнего равенства следуют условия теоремы.
Доказано.
Примеры задачи на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника, вершины которого лежат в серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
Ответ: $20$ см.
Пример 2
Дан треугольник $ABC$. Точки $N\ и\ M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).
Рисунок 5.
Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.
Решение.
Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит
По теореме 1, $AC=2MN$. Получаем:
Ответ: $28$ см.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Средняя линия треугольника — свойства, признаки и формулы
Cвойства средних линий могут различаться. Так, в прямоугольном треугольнике две из трех средних линии перпендикулярны катетам. В то же время третья — по длине аналогична медиане, которую провели к гипотенузе.
Для треугольника, имеющего острые углы и стороны различной длины, средние линии таким свойством не обладают.
Для прямоугольного треугольника является справедливым утверждение, что его средняя линия делит площадь на 4 треугольника, имеющие прямые углы.
В геометрии к свойствам средней линии относят:
- Найти длину средней линии можно разделив длину основания пополам. При этом основание треугольника и его средняя линия являются параллельными.
- Проведя в треугольнике среднюю линию, можно смело утверждать, что он отсек еще один треугольник, который с коэффициентом ½ подобен основному — большому. Вычислить его площадь можно, разделив площадь основного треугольника на 4.
- Проведя в треугольнике все три средние линии, получают четыре треугольника равной площади. При этой центральный из них получил название дополнительного.
- Три средние линии, проведенные в прямоугольном треугольнике, также делят его на 4 меньших треугольника. При этом все они имеют прямые углы.
свойство 1
Из приведенного списка позволяет находить длину средней линии через длину стороны, которая ей параллельна.
Рассмотрим треугольник: Формулу для такого действия, исходя из ниже приведенной схемы, можно выразить так:
Формулу для такого действия, исходя из выше приведенной схемы, можно выразить так:
nb=1/2b
Свойство
Это же свойство № 1 лежит в основе следующей формулы — для нахождения площади треугольника, который образуется в результате отсекания части основного средней линией (S1) нужно площадь основного треугольника (S) разделить на 4:
S1=S/4
Формула для расчета
Теорема
Средняя линия треугольника параллельна основанию и равна её половине.
\(A_1C_1=\frac12AC\)
Доказательство
Дано:
\(\triangle ABC\)
\(A_1C_1\)- средняя линия
Доказать:
\(A_1C_1\parallel AC\)
\(A_1C_1=\frac12AC\)
Рассмотрим \(\triangle BA_1C_1\) и \(\triangle BAC\):
\(\left\{\begin{array}{l}\angle B\;-\;общий\\\frac{BA_1}{BA}=\frac{BC_1}{BC}=\frac12\end{array}\right.\)
Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.
Следовательно, \(\angle BA_1C_1=\angle BAC\) , как соответственные элементы подобных треугольников. Следовательно \(A_1C_1\parallel AC\) по признаку параллельности.
Кроме того, из подобия следует, что \(\frac{A_1C_1}{AC}=\frac12\)
Следовательно, \(A_1C_1=\frac12AC\)
Утверждение доказано.
Примечание
Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
. - У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
. - Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
. - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные. Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства и признаки равнобедренного треугольника
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство | Углы при основании равнобедренного треугольника | Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак | Высота треугольника, совпадающая с медианой | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак | Высота треугольника, совпадающая с биссектрисой | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак | Биссектриса треугольника, совпадающая с медианой | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
| Равнобедренным треугольником называют треугольник, у которого две стороны равны.Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство: углы при основании равнобедренного треугольника | |
| Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак: два равных угла треугольника | |
| Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
| В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак: высота треугольника, совпадающая с медианой | |
| Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак: высота треугольника, совпадающая с биссектрисой | |
| Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак: биссектриса треугольника, совпадающая с медианой | |
| Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение равнобедренного треугольника |
|
| Свойство углов при основании равнобедренного треугольника |
| Свойство:Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
| Признак:Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
| Свойство:В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
| Признак:Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
| Признак:Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
| Признак:Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
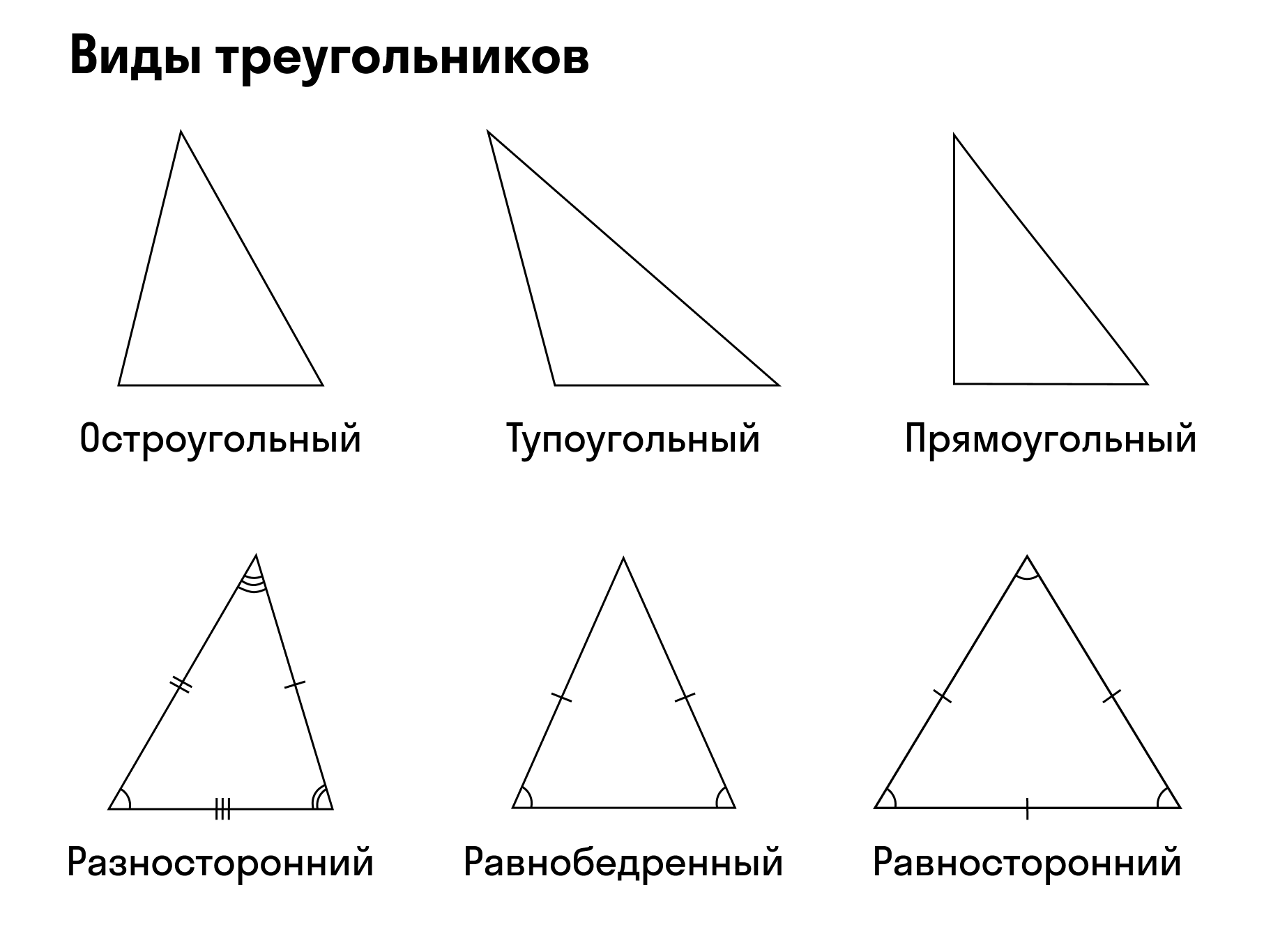
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Средняя линия – это.
Вообще, этот термин в геометрии весьма распространен.
Средняя линия – это отрезок, проходящий через противоположные стороны, и который делит их ровно на две одинаковых части.
Средняя линия есть практически у каждой геометрической фигуры. Например, у четырехугольников она выглядит вот так:
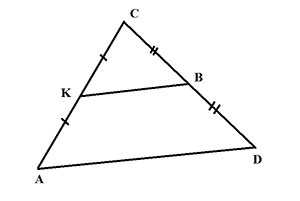
А вот так у треугольников:
И наконец, в случае трапеции изображение средней линии будет вот таким:
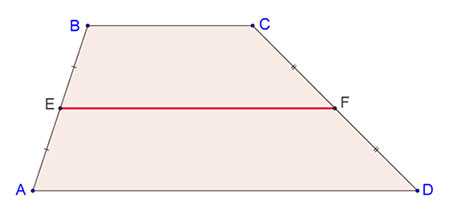
На данном рисунке показана трапеция ABCD. Если кто забыл, то у такой фигуры две противоположные грани расположены на параллельных прямых.
Они называются основаниями. А оставшиеся стороны, которые соответственно не параллельны друг другу, это боковые.
Так вот в нашем случае мы имеем среднюю линию EF, которая делит боковые стороны АВ и СD на две половинки. То есть:
AE = EB и СF = FD
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
. - Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.
Срединный треугольник
Это особый вид фигуры с тремя вершинами, который строится на средних линиях. Поскольку любой треугольник имеет всего три линии указанного вида, то вместе они образуют новую фигуру, вершины которой расположены на серединах сторон исходной.

Построенный геометрический объект делит исходную фигуру на четыре одинаковые части. Доказать это можно следующим образом: если начертить срединный треугольник и обозначить черточками все его стороны, а также длины сторон исходного геометрического объекта, то можно увидеть, что сам он, а также три других фигуры при вершинах исходной имеют по три одинаковых стороны. Иными словами, выполняется признак их подобия. Равенство сторон всех четырех фигур говорит об одинаковом значении их площадей.
Еще одним интересным свойством срединной фигуры является возможность построения внутри нее точно такого же геометрического объекта. Он также будет подобен исходному треугольнику, но уже будет иметь в 8 раз меньшую площадь. Если продолжать такие геометрические построения, то площади срединных треугольников будут становиться все меньше, а пространство на плоскости, которое они будут покрывать, стремится к гравитационному центру исходной фигуры.
Таким образом, формула длины средней линии получается исходя из признака подобия треугольников по углу и двум прилежащим сторонам. Она всегда составляет половину от противоположной стороны. При выполнении геометрического построения срединного треугольника образуются четыре новых фигуры, которые подобны исходной. Гравитационные центры первоначального геометрического объекта и срединной фигуры совпадают.











![Math-public:srednyaya_liniya_treugolnika [президентский фмл №239]](http://rwvt.ru/wp-content/uploads/c/7/3/c7318b00b69359c7a5c16acdb0573e21.jpeg)



















