Подобие треугольников: признаки и свойства

Второй признак подобия треугольников, доказательство

Если две сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны двум дру­гим сто­ро­нам дру­го­го тре­уголь­ни­ка, а углы, за­клю­чён­ные между этими сто­ро­на­ми, равны, то такие тре­уголь­ни­ки по­доб­ны.

Дано: ;  ; ;  (см. рис. 3).

До­ка­зать: по­до­бие дан­ных тре­уголь­ни­ков  . 

Рис. 3. Ил­лю­стра­ция к до­ка­за­тель­ству

До­ка­за­тель­ство

Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков, тре­уголь­ни­ки по­доб­ны, если два угла од­но­го со­от­вет­ствен­но равны двум углам дру­го­го. По­это­му для до­ка­за­тель­ства того, что , необ­хо­ди­мо до­ка­зать, что угол  равен углу  (угол  равен углу  по усло­вию).

По­стро­им тре­уголь­ник  (см. рис. 4), у ко­то­ро­го , а . Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков  (при­знак по­до­бия по двум углам). 

Рис. 4. Ил­лю­стра­ция к до­ка­за­тель­ству

Из по­до­бия этих тре­уголь­ни­ков сле­ду­ет, что сто­ро­на  от­но­сит­ся к сто­роне  как сто­ро­на  от­но­сит­ся к сто­роне :

Из усло­вия из­вест­но, что . Сле­до­ва­тель­но, . Таким об­ра­зом, .

По­лу­ча­ем, что тре­уголь­ни­ки  и  равны, так как у них равны две сто­ро­ны и угол между ними ( – общая сто­ро­на,  и , по­сколь­ку  и ).

От­сю­да сле­ду­ет, что , а так как , то .

У тре­уголь­ни­ков  и : , а . Со­глас­но пер­во­му при­зна­ку по­до­бия тре­уголь­ни­ков эти тре­уголь­ни­ки по­доб­ны: . Что и тре­бо­ва­лось до­ка­зать.

Пропорциональные отрезки

Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как

Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:

Другой пример – это отношение между диагональю квадрата и его стороной.

Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD

Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:

Если отношение отрезка AB к А₁В₁ равно отношению отрезка СD к С₁D₁, то говорят, что отрезки AB и CD пропорциональны отрезкам А₁В₁ и С₁D₁. Например, пусть

Получается, AВ и CD пропорциональны А1В1 и С1D1

Важно отметить, что пропорциональны могут быть также сразу три и более отрезка

Конгруэнтные многогранники

Для двух многогранников с одинаковым комбинаторным типом (то есть с одинаковым количеством ребер E

, одинаковым количеством граней и одинаковым количеством сторон на соответствующих гранях) существует набор измеренийE, которые могут установить, действительно ли многогранники конгруэнтны. Число является точным, что означает, что менееE измерений недостаточно, если многогранники являются общими для своего комбинаторного типа. Но для особых случаев можно использовать меньшее количество измерений. Например, у куба 12 ребер, но 9 измерений достаточно, чтобы решить, конгруэнтен ли многогранник этого комбинаторного типа данному правильному кубу.

Свойства подобных треугольников

Два важнейших свойства: связь периметров и связь площадей.

3.1. Периметры подобных треугольников

Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:

Запишем равенство из определения подобия. Поскольку $\Delta ABC\sim\Delta MNK$, стороны этих треугольников пропорциональны:

\

Здесь число $\color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:

\

Или, что то же самое:

\

Периметр треугольника $MNK$:

\

Периметр треугольника $ABC$:

\

Итого получаем равенство

\

Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:

\

В любом случае, мы получили отношение, которое и требовалось доказать.

3.2. Площади подобных треугольников

Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:

Поскольку $\Delta ABC\sim\Delta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:

\

Кроме того, стороны подобных треугольников пропорциональны:

\

В частности, из этого равенства следует, что

\

Или, что то же самое:

\

Площадь треугольника $MNK$:

\

Площадь треугольника $ABC$:

\

Получаем равенство

\

Перепишем в виде отношения:

\

Что и требовалось доказать.

Впрочем, ничто не мешает взять уже известную формулу:

\

Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)

3.3. Элементы подобных треугольников

Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:

В этом случае высоты $CD\bot AB$ и $KL\bot MN$ относятся как

\

Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.

Гиперболические многообразия

Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.

С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.

Лемма о подобных треугольниках

Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.

Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MN\parallel AB$ отсекает треугольник $MNC$:

Докажем, что $\Delta ABC\sim \Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.

Углы $ABC$ и $MNC$ — соответственными при $MN\parallel AB$ и секущей $BC$. Следовательно, они равны: $\angle ABC=\angle MNC$.

Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.

Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию

\

Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

\

Это равенство — второе в искомом:

\

Осталось доказать первое равенство. Дополнительное построение: прямая $KN\parallel AC$:

Поскольку $AM\parallel KN$ (по построению) и $AK\parallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.

Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

\

Учитывая, что $AK=MN$, получаем

\

Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников

\

Что и требовалось доказать.

Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:

Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда

\

Определение подобных треугольников

В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:

Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.

Пусть есть два треуг-ка, ∆AВС и ∆А₁В₁С₁, у которых соответственно равны углы:

Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁.

Можно дать такое определение подобных треугольников:

Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:

Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:

Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:

Это значит, что коэффициент подобия в данном случае равен 3

Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:. Задание

∆AВС подобен ∆DEF. Известно, что

Задание. ∆AВС подобен ∆DEF. Известно, что

Найдите длину ЕF.

Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:

Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:

Задание. ∆AВС и∆DEF – подобные. Известно, что

Найдите длину ЕF.

Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:

Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:

Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников. Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице

Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.

Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.

Решение. Пусть подобны ∆ AВС и ∆А₁В₁С₁, причем

Периметр ∆AВС можно вычислить так:

Мы доказали утверждение, сформулированное в условии.

Определение сравнения в аналитической геометрии

В евклидовой системе конгруэнтность фундаментальна; это аналог равенства для чисел. В аналитической геометрии конгруэнтность может быть определена интуитивно следующим образом: два отображения фигур в одну декартову систему координат конгруэнтны тогда и только тогда, когда для любых

двух точек в первом отображении евклидово расстояние между ними равно евклидову расстоянию между соответствующими точки во втором отображении.

А государства более формальное определения , что два подмножества A

иB из евклидова пространстваRп называется конгруэнтным , если существует изометрияп :Rп →Rн (элемент из евклидовой группыЕ (п )) сF (A ) =B . Конгруэнтность — это отношение эквивалентности .

Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 16. Подобие треугольников. Задачи на доказательство

Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников! 

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. 

Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы. 

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение. 

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем. 

Вы научитесь также применять подобие треугольников для расчетных задач (не только для доказательств).

Урок 34. Решение задач на применение первого признака подобия треугольников

Содержание (быстрый переход):

Основная дидактическая цель урока: сформировать у учащихся навыки решения задач на применение первого признака подобия треугольников.

Ход урока

II. Актуализация знаний учащихся

1. Теоретический опрос.

1) Доказать теорему, выражающую первый признак подобия треугольников. (Один ученик готовит доказательство теоремы у доски. Заслушать после проведения фронтального теоретического опроса.)

2. Фронтальный теоретический опрос.

• Сформулируйте первый признак подобия треугольников.
• Чему равно отношение периметров подобных треугольников?
• Какие треугольники называются подобными?
• Сформулируйте теорему об отношении площадей подобных треугольников.

III. Решение задач по готовым чертежам

Решить задачи (самостоятельно).

(Один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки. Учитель индивидуально проверяет домашнее задание.)

1. Рис. 7.17. Найти: ВС, MN.
2. Дано: DE||АС (рис. 7.18). Найти: АВ, ВС.
3. Дано: а||b (рис. 7.19). Найти: х, у.
4. Рис. 7.20. Найти: BD.
5. Рис. 7.21. Найти: СО, ВО.
6. Рис. 7.22. Найти: ВС.

Ответы к задачам по готовым чертежам:

1. ВС =3,2, MN= 22,4.
2. АВ= 18, ВС= 12.
3. х = 4, у = 5.
4. BD = 8.
5. СО = 4, ВО = 12.
6. ВС= 15.

IV. Решение задач

1. Работа в рабочих тетрадях.

Решить задачу № 58. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)

2. Решить задачу № 554 (работа в парах).

Наводящие вопросы.

• Есть ли на рисунке подобные треугольники? Почему вы так считаете?
• Найдите коэффициент подобия этих треугольников?
• Каким соотношением связаны сходственные стороны AM и BMP DM и СМ?

3. Решить задачу № 556 (с последующим обсуждением решения).

Вопросы для обсуждения.

• Почему ∠O = ∠CАС₁? (Это соответственные углы при параллельных прямых АС₁ и OD и секущей ОА.)
• Почему ∠OAB = ∠C? (Это соответственные углы при параллельных прямых АВ и CD и секущей АС.)
• Почему ОА : АС = ОВ : АС₁? (Это сходственные стороны подобных треугольников.)
• Докажите, что АС₁ = BD. (BAC₁D — параллелограмм, так как АВ||CD по условию задачи, АС₁||BD как противолежащие стороны параллелограмма.)
• Объясните, каким образом из равенств ОА : АС = ОВ : AС₁ и AC₁ = BD получилось равенство OA : OB = АС : BD.

4. Решить задачу N° 557 (а). (На доске подготовить рисунок. Записать краткое решение задачи.)

Наводящие вопросы.

• Есть ли на рисунке подобные треугольники? Докажите их подобие.
• Составьте отношение сходственных сторон и найдите АС.

V. Самостоятельное решение задач

1. Решить задачи № 557 (б), 552 (в).

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:

• оценка «5» — правильно решены две задачи;
• оценка «4» — одна из задач решена правильно, а при решении второй задачи допущены незначительные ошибки;
• оценка «3» — правильно решена одна задача или при решении двух задач допущены незначительные ошибки;
• оценка «2» — не ставится.

2. Решить дополнительную задачу.

Диагонали трапеции ABCD с основаниями AD и ВС пересекаются в точке О. Периметры треугольников ВОС и AOD относятся как 2 : 3, АС = 20. Найдите длины отрезков АО и ОС.

VI. Рефлексия учебной деятельности

1. Сформулируйте первый признак подобия треугольников.
2. Сколько пар равных углов нужно найти, чтобы доказать подобие треугольников?
3. Сколько пар равных углов нужно найти у прямоугольных (равнобедренных) треугольников, чтобы данные треугольники были подобны?
4. Могут ли быть подобными равносторонние треугольники?

Домашнее задание

1. Повторить П. 61.
2. Решить задачи № 552 (а, б), 557 (в), 558.
3. Решить дополнительную задачу.

В трапеции ABCD (AD и ВС — основания) точка К лежит на стороне CD, причем СК : KD = 1 : 2. АК пересекает BD в точке О. Докажите, что если ВС : AD = 1 : 2, ВО = OD.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 34. Решение задач на применение первого признака подобия треугольников.

Вернуться к Списку уроков Тематического планирования.

Урок 35. Второй и третий признаки подобия треугольников

Содержание (быстрый переход):

Основные дидактические цели урока: рассмотреть второй и третий признаки подобия треугольников; показать применение второго и третьего признаков подобия треугольников при решении задач.

Ход урока

II. Актуализация знаний учащихся

1. Работа в рабочих тетрадях.

Решить задачу № 57 (самостоятельно с последующим обсуждением решения).

Наводящие вопросы.

• Докажите, что ΔABF ~ ΔCDF.
• Чему равен коэффициент подобия треугольников ABF и CDF?
• Найдите отношение сторон BF и DF.
• Чему равно значение DF?

2. Решение задач по готовым чертежам (самостоятельно). (В тетрадях записать краткое решение.)

• 1) Дано: ∠N = ∠A, ВС = 12 см, MN = 6 см, CN = 4 см (рис. 7.27). Найти: АС.
• 2) Дано: ВС ⊥ АС, EF ⊥ AB, ВС = 12 см, EF = 6 см, АЕ = 10 см (рис. 7.28). Найти: АВ.
• 3) Дано: ∠3 = ∠1 + ∠2, CD = 4 см, ВС = 9 см (рис. 7.29). Найти: АС.

3. Обсуждение решений задач, с которыми не справилось большинство учащихся.

III. Работа по теме урока

1. Формулировка темы урока.

• Сформулируйте первый признак равенства треугольников.
• Существуют ли еще какие-либо признаки подобия треугольников?

2. Сформулировать другие признаки подобия треугольников (работа в группах).
3. Доказать второй и третий признаки подобия треугольников.

Второй признак подобия треугольников

Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

(Учащиеся записывают в тетрадях план-конспект доказательства теоремы.)

План-конспект доказательства теоремы

4. Составить план-конспект доказательства третьего признака подобия треугольников. (Учитель делит класс на группы. На обсуждение дается 5 мин. Далее заслушивают представителей групп, в обсуждении решения участвует весь класс.)

Третий признак подобия треугольников

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

План-конспект доказательства теоремы

IV. Закрепление изученного материала

1. Работа в рабочих тетрадях.

Решить задачи № 59, 60 (работа в парах). (Учитель контролирует работу менее подготовленных учащихся и по мере необходимости оказывает индивидуальную помощь.)

Задача № 59. Наводящие вопросы.

• Каким является ∠C для треугольников АВС и MNC?
• Чему равно отношение сторон, заключающих этот угол (АС : CN и ВС : СМ)?
• Что можно сказать о сторонах АС и ВС треугольника АВС и сторонах CN и СМ треугольника MNC?
• Какой признак подобия треугольников был применен при доказательстве подобия треугольников MNC и АВС?

Задача № 60. Наводящие вопросы.

• Чему равно отношение сторон MN и CD, МР и СЕ, NP и DE треугольников MNP и CD ЕР
• Что можно сказать о сторонах треугольников MNP и CDE?
• Укажите признак, на основании которого треугольники MNP и CDE подобны.

(Учащиеся, успешно справившиеся с решением задач, решают дополнительные задачи.)

2. Решить дополнительные задачи.

1) В треугольниках АВС и А₁В₁С₁, BE и В₁Е₁ — биссектрисы, ∠B = ∠B₁, АЕ : ЕС = А₁Е₁ : Е₁С₁. Докажите, что ΔАВЕ ~ ΔА₁В₁Е₁.

2) В треугольнике АВС АВ = 4, ВС = 6, АС = 7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ = 5,25, ME = 4,5, АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что ΔАРВ равнобедренный.

V. Рефлексия учебной деятельности

1. Сформулируйте второй (третий) признак подобия треугольников.
2. Две стороны одного треугольника пропорциональны двум сторонам другого. В каком случае данные треугольники будут подобны?
3. Подобны ли равнобедренные треугольники, если у них углы между боковыми сторонами равны?
4. Подобны ли равнобедренные треугольники, если боковая сторона и основание одного из них пропорциональны боковой стороне и основанию другого?
5. Могут ли быть подобными прямоугольные треугольники, если катеты одного из них пропорциональны катетам другого?

Домашнее задание

1. П. 62, 63, вопросы 6, 7 (учебник, с. 158, 159).
2. Решить задачи № 559, 560 (б), 561.
3. Решить дополнительную задачу.

В треугольниках ABС и A₁B₁C₁, BD и B₁D₁ — медианы, ∠A = ∠A₁, ∠BDA = ∠В₁D₁A₁. Докажите, что треугольник BDC подобен треугольнику B₁D₁С₁.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников.

Вернуться к Списку уроков Тематического планирования.

Треугольник. Подобные треугольники. Свойства подобных треугольников.

Проанализируем пару треугольников, которые визуально похожи.

Стороны второго треугольника в соотношении со сторонами первого меньше в два раза:

Под соотношением отрезков AB и А₁В₁ понимается соотношение их длин. Если соотношения пар отрезков равны, то указывают, что отрезки пропорциональны:

.

У представленных треугольников углы попарно тождественны. Стороны, расположенные напротив одинаковых углов, соразмерны.

Такие треугольники именуют подобными. Стороны, расположенные напротив одинаковых углов, принято обозначать как сходственные. Следовательно, подобными называются треугольники, у которых углы попарно тождественны, а сходственные стороны соразмерны. Подобие треугольников обозначается так:

Соотношение сходственных сторон подобных фигур именуют коэффициентом подобия. В представленном примере он равен двум.

Конгруэнтные конические сечения

Два конических сечения конгруэнтны, если их эксцентриситет и один другой отдельный параметр, их характеризующий, равны. Их эксцентриситет определяет их формы, равенства которых достаточно для установления сходства, а второй параметр затем устанавливает размер. Поскольку две окружности , параболы или прямоугольные гиперболы всегда имеют одинаковый эксцентриситет (в частности, 0 в случае окружностей, 1 в случае парабол и в случае прямоугольных гипербол), две окружности, параболы или прямоугольные гиперболы должны иметь одинаковый эксцентриситет. только одно другое общее значение параметра, определяющее их размер, чтобы они были конгруэнтными. 2 {\displaystyle {\sqrt {2}}}

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

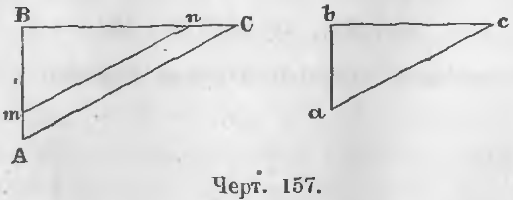
Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

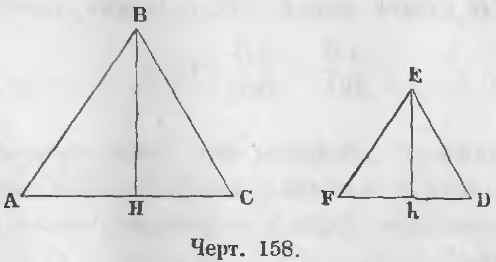
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).