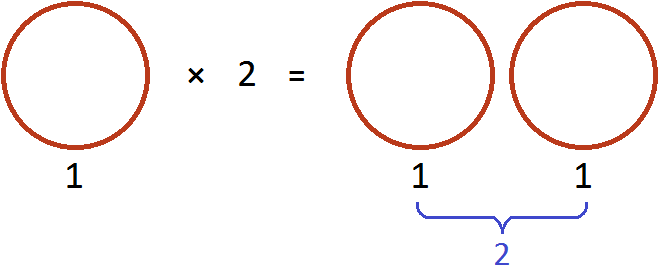Деление обыкновенных дробей: правила, примеры, решения

Видео математика 5 класс сложение и вычитание дробей с одинаковыми знаменателями

Прежде чем приступить к пояснению, следует сделать акцент на понятии «натуральное число».

Натуральными считаются все числа от 1 и до бесконечности. Единственное условие положительность числа. Это значит, что оно не должно быть с «-«, например -2. Если мы видим минус, значит оно отрицательное. Дроби и числа со знаком «-» к натуральным не относятся.

Используя дроби можно выполнить запись деления двух абсолютно любых натуральных чисел.

Если в процессе мы получаем целое число, тогда оно будет натуральным. Если же целое число у нас не получается, тогда частное называется дробным.

Делим любое натуральное число

Если в примере есть одинаковая нижняя часть под черточкой, тогда она выносится за пределы скобок.

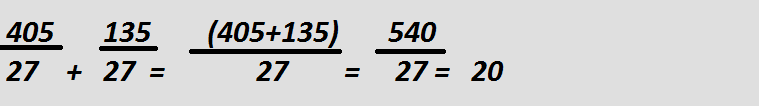
При делении суммы на какое-то число, мы можем отдельно провести деление каждой слагаемой суммы. В конце все части необходимо сложить вместе.

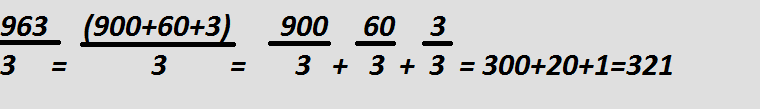
Сокращение дробей

Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.

Пример 1. Сократить дробь 8/12

Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:

8/12 = 8:4 / 12:4 = 2/3

Пример 2. Сократить дробь 10/25

Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:

10/25 = 10:5 / 25:5 = 2/5

Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.

Сократите следующие дроби:

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения
. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

По определению имеем:

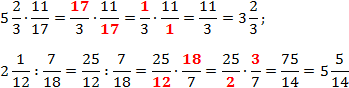
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать

Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Урок математики по теме «Деление дробей в уравнениях»

Разделы: Математика

Форма урока: объяснение нового материала.

Цели урока:

Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.

Воспитательная: воспитывать самостоятельность, аккуратность

Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.

Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.

Этапы урока

Время (мин)

Слайды

Организационный момент.
2
Слайд 1

Устная работа и повторение ранее изученного
8
Слайды 2, 3, 4, 5,6

Формирование новых знаний и умений
10
Слайды 7, 8

Физкультминутка
2
Слайды 9, 10

Закрепление нового материала
5
Слайд 11

Проверка знаний (с/р)
10
Слайд 12

Постановка домашнего задания
1
Слайд 13

Подведение итогов урока
2

I. Организационный этап

– Здравствуйте, мы проведем сегодня урок по теме «Деление дробей в уравнених». Откройте тетради, запишите число, классная работа и тему урока. Целью нашего урока является закрепление и проверка умений умножать и делить обыкновенные дроби, а также повторить навыки решения задач и уравнений.

II. Устный опрос учащихся

1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)

– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.

4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)

– Повторим правило деления двух дробей: Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

III. Формирование новых знаний и умений

– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)

– Чтобы решить уравнение необходимо определить какой компонент в уравнении является неизвестным. – Какой? – 1 множитель – Правильно! Чтобы найти неизвестный множитель, что нужно сделать? – Чтобы найти неизвестный множитель необходимо произведение разделить на известный множитель. – Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.

– А теперь давайте проверим ваше умение решать задачи.

– Сколько всего прошел лыжник ? (26 км) – Сколько километров прошел в первый день? (неизвестно) – Сколько километров прошел во второй день? (неизвестно) – Какую величину, с какой сравнивают? – Что возьмем за х? – Как найти дробь от числа? – Сколько километров прошел за два дня? – Как найти? – Составим уравнение.

– 14 км лыжник прошел во второй день

26 – 14 = 12 км лыжник прошел в первый день.

– Вспомним что такое 1% (одна сотая) – Какой дробью запишем 75% (75/100 = 3/4) – Сколько грибов собрала белка? (неизвестно) – Сколько грибов собрал бельчонок? (неизвестно) – Какую величину, с какой сравнивают? – Что обозначим за икс? – Как найти дробь от числа? – Сколько собрали вместе белка и бельчонок? – Составим уравнение.

200 грибов собрала белка 350 – 200 = 150 грибов собрал бельчонок

IV. Физкультминутка

– Встаем и выполняем несколько упражнений.

V. Закрепление нового материала

– Сколько собрал Митя? – Сколько собрал Коля? – Какую величину, с какой сравнивают? – Что обозначим за икс? – Как найти дробь от числа? – Сколько собрали вместе мальчики?

28 грибов собрал Митя

64 – 28 = 36 грибов собрал Коля

VI. «Математический выбор»

Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:

2) 2)

3) 3)

4) 4)

Уравнения, оцениваемые в 6 баллов:

2)

3)

4)

Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.

Каждый выбирает себе уравнения по «плечу». Учитель во время работы оценивает учеников.

VII. Итог урока

– С каким настроением вы сегодня работали на уроке? – Какая задача для вас была самой интересной? – Ребята чему мы научились на сегодняшнем уроке? – Как найти часть от числа? – Как найти неизвестный множитель?

VIII. Домашнее задание

– С листов решить любые три уравнения, из тех которые не решали в классе.

Правильные дроби

Правильной дробью называется обыкновенная дробь $\frac{m}{n}$, у которой числитель меньше знаменателя, т.е. $m

Пример 1

Например, дроби $\frac{1}{3}$, $\frac{9}{123}$, $\frac{77}{78}$, $\frac{378567}{456298}$ являются правильными, так как в каждой из них числитель меньше знаменателя, что отвечает определению правильной дроби.

Существует определение правильной дроби, которое базируется на сравнении дроби с единицей.

Обыкновенная дробь $\frac{m}{n}$ является правильной, если она меньше единицы:

Пример 2

Например, обыкновенная дробь $\frac{6}{13}$ является правильной, т.к. выполняется условие $\frac{6}{13}

Примеры решения

Несмотря на то что операция по превращению довольно простая, для её успешного применения необходим опыт, поэтому следует потренироваться не только в простом преобразовании, но и увидеть полезность действий на практике. Вот некоторые примеры, рассчитанные на учащихся четвёртых классов, рекомендуемые к самостоятельному решению:

1. Выполнить перевод смешанной дроби в неправильную форму записи: 4 4/9 = (4*9 + 4)/9 = (36 + 4)/9 = 40/9; 5 7/15 = ((5*15) + 7)/15 = (75 + 7)/15 = 82/15; 2 3/5 = ((2*5)+3)/5 = (10 + 3)/5 = 13/5.
2. Перевести неправильное выражение в правильное. В соответствии с алгоритмом, нужно выделить целую часть. Для этого следует поделить числитель на знаменатель или выполнить ряд преобразований: 12/5 = (10+2)/5 = 10/5 + 2/5 = 2+2/5 = 2 2/5; 11/3 = (9+2)/3 = 3+2/3 = 3 2/3; 19/14 = (14+ 5)/14 = 14/14 + 5/14 = 1 + 5/14 = 1 5/14.
3. Решить уравнение: 1/12 + 3 2/4 + 19/12 — 2. Чтобы решить этот пример, необходимо свести все выражения к одной форме, то есть смешанную запись нужно привести к неправильному типу. 3 2 /24 = 3 + 2/24 = 3/1 + 2/24 = (24*3 + 2)/24 = 74/24. Полученное значение можно упростить, сократив обе части на 2: 74/24 = 37 / 12. Теперь исходное выражение примет вид: 1/12 + 37/12 + 19/12 — 2 = ((1+37+19)/12) — 2 = 57/12 — 2. Осталось преобразовать неправильную дробь в смешанную и рассчитать ответ: 57/12 — 2 = 9/12 + 48/12 — 2 = 4+9/12 — 2 = 2 + 9/12 = 2 9/12.

В интернете существуют сервисы, позволяющие в автоматическом режиме выполнять перевод из одной формы записи в другую. Чтобы воспользоваться услугами таких онлайн-калькуляторов, необязательно знать принцип преобразования. Доступ к услугам не требует регистрации или введения каких-либо персональных данных. Нужно просто иметь гаджет с подключённым интернетом и любой веб-браузер. Всё, что требуется от пользователя — ввести в предлагаемую форму исходную дробь и нажать кнопку «Рассчитать». Через несколько секунд на экран будет выведен ответ.

Пример решения задачи

Для закрепления теоретического материала специалисты рекомендуют решить задачу. Ее условие звучит следующим образом: доказать делимость суммы смешанных чисел 202 и 112 на пятнадцать. Задание решается по такому алгоритму:

1. Запись числового выражения: (202[2/4] + 112)/15.
2. Преобразование первого смешанного числа в неправильную дробь (можно сократить числитель и знаменатель на двойку): 202=405/2.
3. Перевести вторую смешанную дробь: 112=225/2.
4. Сложение: 405/2 + 225/2 = 630/2 = 315.
5. Проверка делимости на 15: на пятерку делится, поскольку заканчивается на 5 и на тройку также, т. к. 3+1+5=9 (9/3=3).

Следует отметить, что сумма двух смешанных дробей делится на пятнадцать без остатка, поскольку ее можно поделить на три и пять, из которых состоит делитель 15.

Умножение двух обыкновенных дробей

Правило умножения обыкновенных дробей:

Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:

Пример 1

Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.

Решение.

Воспользуемся правилом умножения обыкновенных дробей:

\

Ответ: $\frac{15}{77}$

Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.

Пример 2

Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.

Решение.

Используем правило умножения обыкновенных дробей:

\

В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:

\

Краткое решение:

\

Ответ: $\frac{1}{24}.$

При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.

Пример 3

Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.

Решение.

Воспользуемся формулой умножения обыкновенных дробей:

\

Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:

\

Ответ: $\frac{1}{20}.$

При умножении дробей можно применять переместительный закон:

Более быстрый способ

В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:

1. Посчитать, сколько цифр стоит после запятой. Например, у дроби 1,75 таких цифр две, а у 0,0025 — четыре. Обозначим это количество буквой $n$.
2. Переписать исходное число в виде дроби вида $\frac{a}{{{10}^{n}}}$, где $a$ — это все цифры исходной дроби (без «стартовых» нулей слева, если они есть), а $n$ — то самое количество цифр после запятой, которое мы посчитали на первом шаге. Другими словами, необходимо разделить цифры исходной дроби на единицу с $n$ нулями.
3. По возможности сократить полученную дробь.

Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:

Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому $n=2$. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64. Переходим ко второму шагу: ${{10}^{n}}={{10}^{2}}=100$, поэтому в знаменателе стоит именно сто. Ну а затем остаётся лишь сократить числитель и знаменатель.:)

Ещё один пример:

Здесь всё чуть сложнее. Во-первых, цифр после запятой уже 3 штуки, т.е. $n=3$, поэтому делить придётся на ${{10}^{n}}={{10}^{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.

Наконец, последний пример:

Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.

Действия с дробями 5 класс

В пятом классе учатся выполнять все арифметические действия с дробями.

Все действия с дробями выполняются по правилам, и надеяться на то, что не выучив правило все получится само сабой не стоит. Поэтому не стоит пренебрегать устной частью домашнего задания по математике.

Мы уже поняли, что запись десятичной и обыкновенной дроби различны, следовательно и арифметические действия будут выполняться по-разному. Действия с обыкновенными дробями зависят от тех чисел, которые стоят в знаменателе, а в десятичной-после запятой справа.

Для дробей, у которых знаменатели одинаковые, алгоритм сложения и вычитания очень прост. Действия выполняем только с числителями.

Для дробей с разными знаменателями нужно найти Наименьший Общий Знаменатель (НОЗ).

Это то число, которое будет делиться без остатка на все знаменатели, и будет наименьшим из таких чисел, если их несколько.

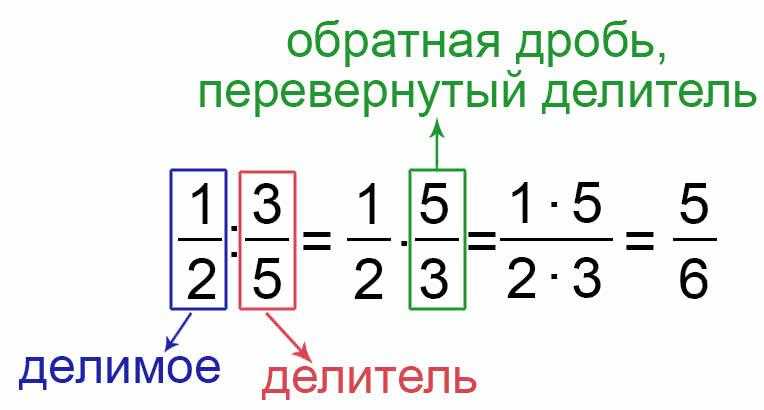
Для сложения либо вычитания десятичных дробей, нужно записать их в столбик, запятая под запятой, и уравнить количество десятичных знаков если это требуется.

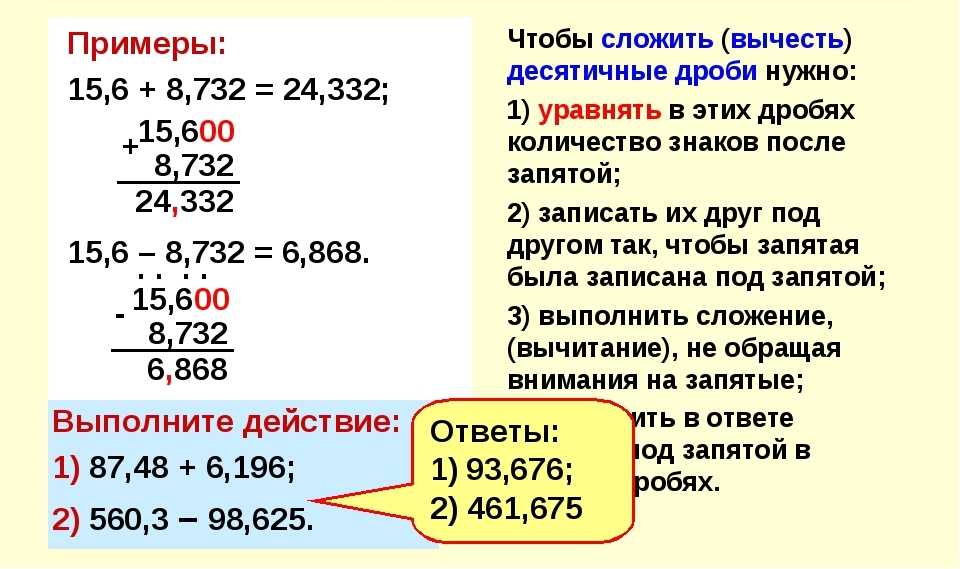
Чтобы перемножить обыкновенные дроби просто найди произведение числителей и знаменателей. Очень простое правило.

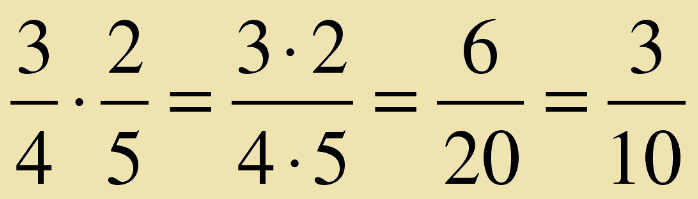
Деление выполняется по следующему алгоритму:

1. Делимое записать без изменения
2. Деление превратить в умножение
3. Делитель перевернуть (записать обратную дробь делителю)
4. Выполнить умножение

Как перевести обыкновенную дробь в периодическую

Для перевода обыкновенной дроби в периодическую следует выполнить определенные шаги. Сначала необходимо привести дробь к неправильному виду, чтобы числитель был больше знаменателя. Затем производится деление числителя на знаменатель, записывая результат столбиком. Если после некоторого разряда остаток начинает повторяться, то эта последовательность цифр становится периодической частью десятичной записи. В случае, когда остаток становится равным нулю, это означает, что десятичная запись не имеет периода. Если периодических чисел нет, то десятичная дробь будет рациональной и конечной. В периодической дроби непериодическую часть можно записать в скобки или отдельно, в зависимости от требований задачи или предпочтений

Важно помнить, что периодическая десятичная дробь можно представить в виде обыкновенной, восстановив искомую дробь по ее десятичной записи

Приведение дробей к общему знаменателю

Представляешь, любые две дроби можно привести к общему знаменателю! Ну, если тебя это не поразило, ты, наверное, не понял о чем я. Вот смотри. Есть две дроби \( \displaystyle  1/3\) и \( \displaystyle  3/5\).

Тебе надо изменить эти дроби так, чтоб значение дробей не поменялось, но в знаменателе у обеих стало одно и то же число. Подскажу лишь, что для этого нужно воспользоваться основным свойством дроби.

Ладно, так и быть, покажу сам: \( \displaystyle  1/3=5/15\); \( \displaystyle  3/5=9/15\). Как ты видишь в знаменателе у обеих дробей \( \displaystyle  15\), и при этом, если сократить дроби, первую на \( \displaystyle  5\), а вторую на \( \displaystyle  3\), то получатся те же \( \displaystyle  1/3\) и \( \displaystyle  3/5\)!

Сказать, как это делается? Так и быть, тебе сегодня везет, читай ниже.

Деление необыкновенной дроби на натуральное число

Используем правило деления дроби на натуральное число:чтобы разделить a b на натуральное число n , необходимо умножить только знаменатель на n . Отсюда получим выражение: a b: n = a b · n .

Правило деления является следствием правила умножения. Поэтому представление натурального числа в виде дроби даст равенство такого типа: a b: n = a b: n 1 = a b · 1 n = a b · n .

Рассмотрим данное деление дроби на число.

Пример 3

Произвести деление дроби 16 45 на число 12 .

Решение

Применим правило деления дроби на число. Получим выражение вида 16 45: 12 = 16 45 · 12 .

Произведем сокращение дроби. Получим 16 45 · 12 = 2 · 2 · 2 · 2 (3 · 3 · 5) · (2 · 2 · 3) = 2 · 2 3 · 3 · 3 · 5 = 4 135 .

Ответ:
16 45: 12 = 4 135 .

Деление дроби на число

Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?

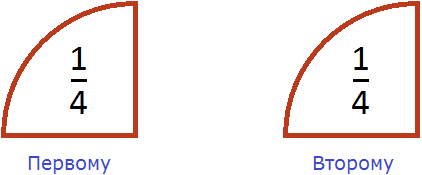
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет  пиццы. Значит каждому достанется по  пиццы.

Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.

Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.

Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.

Итак, требуется разделить дробь  на число 2. Здесь делимым является дробь , а делителем число 2.

Чтобы разделить дробь  на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить  на 

Получили ответ . Значит при делении половины на две части получается четверть.

Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:

Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:

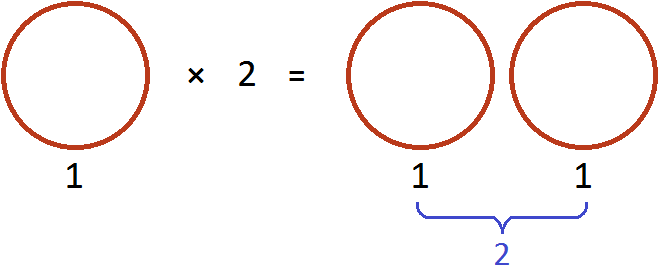
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:

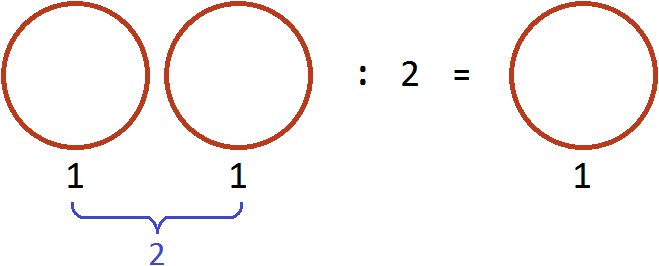
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь 

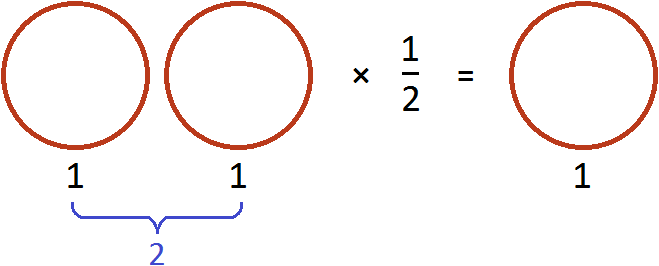
В обоих случаях получился один и тот же результат.

Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить  на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь 

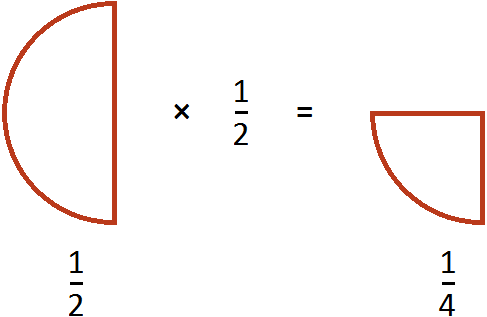
Пример 2. Найти значение выражения 

Умножим первую дробь на число, обратное делителю:

Допустим, имеется четверть пиццы и нужно разделить её на двоих:

Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:

Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5

10 : 2 = 5

Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь 

Как видно результат не изменился. Мы снова получили ответ 5.

Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.

Пример 3. Найти значение выражения

Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь 

Допустим, имелось пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков

Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении  на 6 получается 

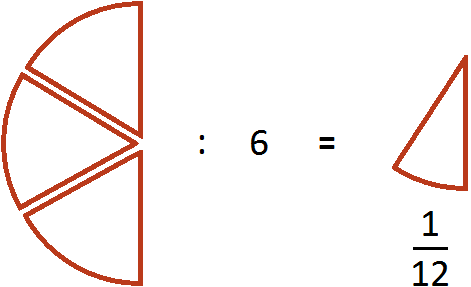
Сложение смешанного числа и правильной дроби

Сложение смешанного числа $a\frac{b}{c}$ и правильной дроби $\frac{d}{e}$ выполняет прибавлением к данной дроби дробной части данного смешанного числа:

\

Пример 7

Выполнить сложение правильной дроби $\frac{4}{15}$ и смешанного числа $3\frac{2}{5}$.

Решение.

Воспользуемся формулой сложения смешанного числа и правильной дроби:

\

По признаку деления на число \textit{5 }можно определить, что дробь $\frac{10}{15}$ — сократима. Выполним сокращение и найдем результат сложения:

\

Итак, результатом сложения правильной дроби $\frac{4}{15}$ и смешанного числа $3\frac{2}{5}$ будет $3\frac{2}{3}$.

Ответ: $3\frac{2}{3}$

Как превратить целое число в обыкновенную дробь

Чтобы превратить целое число 13 в обыкновенную дробь, нужно умножить его на знаменатель 9 и прибавить числитель 7. Получается, что числитель неправильной дроби будет равен 13*9 + 7 = 124, а знаменатель остается неизменным и равен 9. Таким образом, обыкновенная дробь, которая соответствует числу 13, будет равна 124/9. В общем виде, для любого целого числа a и знаменателя b, чтобы превратить целое число в обыкновенную дробь, нужно умножить a на b и прибавить числитель, а знаменатель оставить таким же. Это позволяет нам представить целые числа как дроби и использовать их в математических операциях с другими дробями.

Как число превратить в дробь

Калькулятор покажет как перевести десятичную дробь в обыкновенную дробь, либо в смешанное число. Введите десятичную дробь и калькулятор напишет подробное решение.

Перевод десятичных дробей в обыкновенные дроби

Алгоритм преобразования

Чтобы преобразовать десятичную дробь в обыкновенную дробь нужно выполнить следующие шаги:

• 1 Записать в виде дроби с знаменателем 1:
• 2 Умножать числить и знаменатель на 10 за каждый знак после запятой десятичной дроби. Например для десятичной дроби 0.025 нужно умножить 3 раза на 10, т.к. 3 цифры после запятой. Иначе говоря умножаем на 10 пока числитель не станет целым числом.
• 3 Упростить(сократить) полученную дробь. Чтобы сократить дробь нужно найти наибольший общий делитель числителя и знаменателя дроби.

Рассмотрим на примере числа 0.025 как перевести десятичную дробь в обыкновенную.

Пример Преобразования числа 0.025 в дробь

.

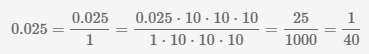Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Примеры преобразования десятичных дробей

Перевод десятичной дроби в обыкновенную дробь

Рассмотрим на примерах процесс преобразования десятичных дробей.

Пример Преобразовать десятичную дробь 0.45 в обыкновенную дробь

.

Сократим дробь с помощью нахождения наибольшего общего делителя числителя и знаменателя и последующего деления полученного числа на числитель и знаменатель, НОД(45,100)=5.

Пример Преобразовать 0.875 в дробь.

.

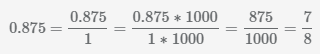Перевод десятичной дроби в смешанную дробь

Если десятичная дробь больше 1, то в результате преобразования получается смешанное число. Целая часть при переводе остается неизменной.

Рассмотрим на примере как переводить число в смешанную дробь.

Пример Преобразовать число 567.35 в смешанное число

.

В результат преобразования получаем смешанную дробь.

Пример Перевести число 1.99 в дробь

.

Умножение дроби на число

Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.

Пример 1. Умножить дробь  на число 1.

Умножим числитель дроби  на число 1

Запись  можно понимать, как взять половину 1 раз. К примеру, если  пиццы взять 1 раз, то получится  пиццы

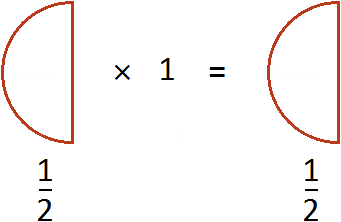
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:

Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется  пиццы:

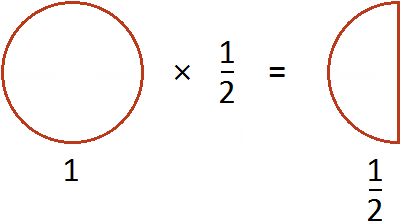
Пример 2. Найти значение выражения 

Умножим числитель дроби  на 4

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Выражение  можно понимать, как взятие двух четвертей 4 раза. К примеру, если  пиццы взять 4 раза, то получится две целые пиццы

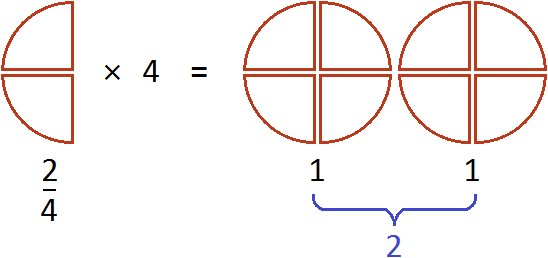
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:

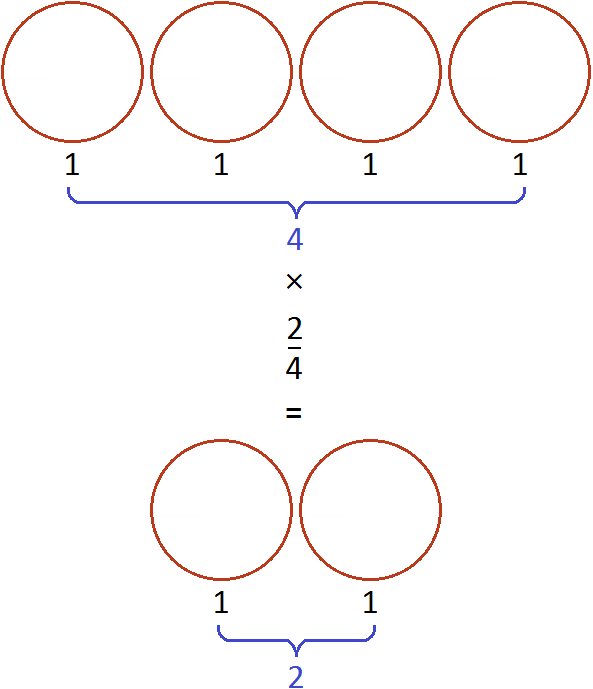
Число, которое умножается на дробь, и знаменатель дроби разрешается , если они имеют общий делитель, бóльший единицы.

Например, выражение  можно вычислить двумя способами.

Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:

Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:

Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:

Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:

А вот к примеру выражение  можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:

Связано это с тем, что число 7 и знаменатель дроби  не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.

Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:

Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать  это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.

Полезные советы и выводы

Для удобства выполнения операций с дробями с целым числом, рекомендуется использовать правильные дроби вместо смешанных чисел.
При умножении дроби на натуральное число необходимо умножать знаменатель, это поможет корректно выполнить операцию.
Необходимо уметь выполнять преобразование смешанной дроби в неправильную и наоборот, так как это может понадобиться при выполнении различных математических операций.
Важно находить общие знаменатели при сложении или вычитании смешанных чисел для получения корректного результата.
Регулярное выполнение упражнений поможет закрепить знания и навыки по работе с дробями с целым числом.

В данной статье мы рассмотрели различные методы работы с дробями с целым числом и дали подробные пошаговые инструкции по каждому методу. Эти знания будут полезны при выполнении задач и решении математических проблем, связанных с дробями. Практикуйтесь, чтобы закрепить полученные навыки и ощутить уверенность в решении подобных задач.

Как записать обыкновенную дробь в виде бесконечной десятичной дроби

Когда мы хотим записать обыкновенную дробь в виде бесконечной десятичной дроби, мы можем следовать нескольким шагам.

Первый шаг — записать натуральное число, которое получится из дроби, если мы просто игнорируем запятую и скобки. Это число будет являться числителем искомой десятичной дроби.

Затем, второй шаг — записать натуральное число, составленное из цифр, которые стоят перед периодом десятичной дроби. Это число будет являться знаменателем искомой десятичной дроби.

И, наконец, вычисляем разность между этими двумя числами, которая будет числителем искомой обыкновенной дроби.

Таким образом, мы можем записать обыкновенную дробь в виде бесконечной десятичной дроби, следуя этим шагам.

Как понять где ставить запятую в десятичной дроби

Правильное расстановка запятых в десятичной дроби может вызывать затруднения у многих людей. Однако есть простой способ понять, где ставить запятую. Сначала записываем дроби, которые нужно перемножить, в столбик. Затем умножаем эти дроби между собой, как если бы это были обыкновенные числа. После этого считаем количество знаков после запятой у каждой дроби и складываем их. Полученную сумму знаков перемещаем справа налево и ставим запятую. Например, у нас есть дроби 0,5 и 0,3. У первой дроби один знак после запятой, а у второй — ноль. Сложив эти числа, мы получаем 1. Перемещаем это число справа налево и получаем 0,01. Итак, правильное расстановка запятых в данном случае будет 0,01.

Как не целое число перевести в дробь

Для примера рассмотрим число 0.625, которое нужно перевести в десятичную дробь по правилам задания. У нас в основании системы счисления будет число 10, так как переводим в десятичную систему.

Умножим дробную часть числа на 10. Получим 6.25. Записываем целую часть — число 6. Умножаем дробную часть 0.25 на 10 и получаем число 2.5. Записываем целую часть — число 2. Последнее умножение даст нам 5.

Итак, результатом перевода числа 0.625 в десятичную дробь будет 0.625 = 0.625.

Основание системы счисления можно выбирать любым, в зависимости от поставленной задачи. В данном примере было выбрано основание 10, так как речь идет о переводе числа в десятичную дробь.

Как перевести десятичную дробь в целое число

Если десятичная дробь не содержит целой части, то ее переводят в обыкновенную дробь. Для этого числительом становится часть числа после запятой, а знаменатель равен единице, сдвинутой вправо на количество разрядов после запятой. Например, 0,3 = 3/10, а 0,125 = 125/1000. Десятичную дробь также можно записывать в виде десятичной обыкновенной дроби, в которой знаменатель является степенью десяти. Например, 0,3 = 3/10, а 0,125 = 125/1000. Чтобы перевести десятичную дробь в целое число, необходимо умножить ее на 10 столько раз, сколько разрядов в ее дробной части, и округлить результат до целого числа. Например, 3,2 = 32, 0,75 = 7,5. Это позволяет представить десятичную дробь в виде целого числа без фракционной части.