Периодические дроби

Дробь и ее виды

Обыкновенная или простая дробь — это число вида a/b , где a — числитель дроби, b — знаменатель дроби. Суть дроби можно объяснить на примере пирога – например, дробь ¼ означает один кусок пирога из 4-ех.

 Правильная — дробь, у которой числитель меньше знаменателя (например, 1/5, 2/9).

 Неправильная — дробь, у которой числитель больше или равен знаменателю (например, 7/2, 5/5).

 Смешанная — дробь, записанная в виде целого числа и правильной дроби. Она представляет собой сумму этого числа и дроби. Любую неправильную дробь можно перевести в смешанную путем выделения целой части (например, 9/4 = 2 ¼).

 Десятичная — дробь со знаменателем 10, 100, 1000 и т.д. (например, 7/10 или 0,7; 9/100 или 0,09). Десятичная дробь записывается в виде целой и дробной части, которые отделяются запятой.

Перевод периодической дроби в обыкновенную

Периодическую бесконечную десятичную дробь можно перевести в обыкновенную дробь.

Рассмотрим периодическую дробь 10,0219(37)

• Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву « k ». У нас « k = 2 ».
• Считаем количество цифр, стоящих после запятой, но до периода десятичной дроби. Обозначаем количество цифр за букву m . У нас « m = 4 ».
• Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа.

Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначаем полученное число буквой « a ». a = 021937 = 21 937

Теперь записываем все цифры, стоящие после запятой, но до периода , в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначаем полученное число буквой « b ». b = 0219 = 219
Подставляем найденные значения в формулу, где « Y » — целая часть бесконечной периодической дроби. У нас « Y = 10 ».

Итак, подставляем все найденные значения в формулу выше и получаем обыкновенную дробь. Полученный ответ всегда можно проверить на обычном калькуляторе.

Источник

Перевод десятичных дробей в периодические

В некоторых случаях, при работе с обыкновенными дробями, возникает необходимость перевести их представление из десятичной в периодическую дробь. Для этого нужно произвести некоторые математические операции, в основе которых лежит знание о том, что каждая цифра, стоящая после запятой в десятичной дроби, обозначает определенную дробь с единицей в знаменателе. Например, в дроби 0.1234 «1» обозначает 1/10, «2» обозначает 2/100 и так далее.

Для перевода десятичной дроби в периодическую необходимо:

1. Находим числитель дроби, равной исходной десятичной дроби. Например, для дроби 0.25 числитель будет равен 25.
2. Записываем этот числитель в знаменатель дроби, в которой за знаком равенства стоит исходная десятичная дробь (25/100 в примере).
3. Сокращаем полученную дробь на наибольший общий делитель ее числителя и знаменателя. Если после этого в знаменателе есть множитель, кроме 2 и 5, это означает, что дробь является периодической.
4. Находим период — группу цифр, которые постоянно повторяются в десятичном представлении периодической дроби. Для этого можно разделить на число и найти остаток от деления на знаменатель.

Например, рассмотрим десятичную дробь 0.142857. По шагам описанной выше процедуры, получим дробь 142857/999999. Сокращаем ее до 1/7. Так как в знаменателе только множители 2 и 5, то это периодическая дробь. Период можно найти, разделив число 142857 на 7 и находя остатки от деления: 1, 3, 2, 6, 4, 5.

Таким образом, перевод десятичных дробей в периодические — это важный инструмент при работе с обыкновенными дробями и дополнительное средство для проверки правильности вычислений.

Перевод смешанной периодической дроби в обыкновенную дробь

Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.

В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

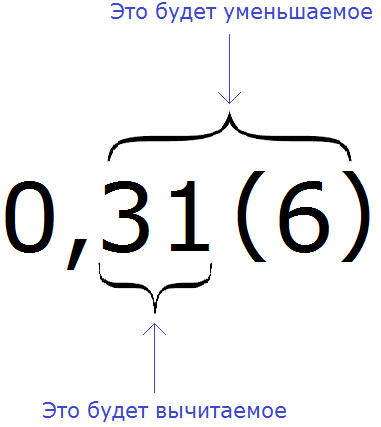
Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)

В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

Получили выражение, которое вычисляется легко:

Получили ответ

Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается

Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

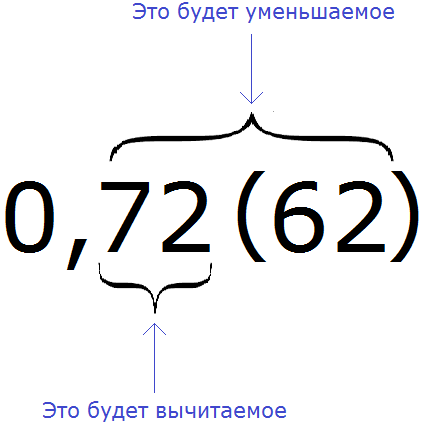
Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)

В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

Получили выражение, которое вычисляется легко:

Получили ответ

Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект? Используй кнопку ниже

Перевод десятичной дроби в обыкновенную дробь

Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:

и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .

Пример 2.
Перевести десятичную дробь 0,02 в обыкновенную дробь.

0,02 это ноль целых и две сотых. Ноль по не записываем, поэтому сразу записываем две сотых

Пример 3.
Перевести 0,00005 в обыкновенную дробь

0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Используются чрезвычайно широко, причем в самых различных сферах человеческой деятельности будь то научные и прикладные вычисления, разработка и эксплуатация различной техники, экономический расчёт и так далее. В виду разного рода причин нередко приходится осуществлять обращение десятичной дроби
, равно как и процесс, обратный ей. Следует заметить, что подобные преобразования
производятся относительно легко, причем в соответствии с определенными правилами и методиками, существующими в математике уже на протяжении многих сотен лет.

Обращение десятичной дроби в простую

Преобразование десятичной дроби
в дробь «обыкновенную » производится достаточно легко и просто. Для этого используется следующая методика: в качестве числителя новой дроби берется число, которое располагается справа от десятичной точки исходного числа, в качестве знаменателя используется число десять, в степени, равной количеству разрядов числителя. Что касается оставшейся целой части, то она сохраняется неизменной. Если же целая часть равна нулю, то после преобразования она просто опускается.

ПРИМЕР 1

Пятьдесят целых двадцать пять сотых равняется пятьдесят целых и двадцать пять разделить на сто равняется пятьдесят целых одна четвертая.

Обращение простой дроби в десятичную

Преобразование простой дроби в десятичную
, по сути дела, является обратной обращению десятичной дроби в простую
. Её осуществление также не вызывает никаких затруднений и является, по сути дела, довольно простым арифметическим действием. Для того чтобы обратить простую дробь в десятичную
нужно разделить числитель на её знаменатель в соответствии с определенными правилами.

ПРИМЕР 1

Необходимо осуществить преобразование обычной дроби
пять восьмых в десятичную дробь
.

При делении пяти на восемь получается десятичная дробь
ноль целых шестьсот двадцать пять тысячных.

Округление результата преобразования простой дроби в десятичную

Следует заметить, что, в отличие от такого процесса, как преобразование десятичной дроби
, эта процедура за частую может длиться бесконечно долго. В таких случаях говорят, что результат процедуры обращения обычной дроби в десятичную
не может быть точным. Впрочем, практика показывает, что в подавляющем большинстве получение идеально точного результата и не требуется. Как правило, процесс деления заканчивается тогда, когда в его ходе уже получены значения тех десятичных долей, которые представляют в каждом конкретном случае практический интерес.

ПРИМЕР 1

Требуется разрезать кусок масла весом один килограмм на девять одинаковых по своей массе частей. При выполнении этой процедуры оказывается, что масса каждой из них равняется 1 / 9 килограмма. Если по всем правилам осуществлять преобразование
этой обычной дроби
в дробь десятичную
, то получится, что масса каждой из получившихся частей равняется ноль целых и один в периоде килограмма.

Округление ведется по стандартным правилам, предусмотренным в арифметике: если первая из «отбрасываемых» цифр имеет значение 5 и более, то последняя из значимых увеличивается на единицу. В противном случае она остается неизменной.

ПРИМЕР 2

Преобразовать обычную дробь
одна восьмых в дробь десятичную.

При делении единицы на восемь получается ноль целых сто двадцать пять тысячных или округлённо — ноль целых тринадцать сотых.

Получаем периодическую дробь

Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.

Итак, делим 1 на 3

Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.

Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.

В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).

В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:

Читается как «ноль целых и три в периоде»

Пример 2. Разделить 5 на 11

Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:

Читается как «ноль целых и сорок пять в периоде»

Пример 3. Разделить 15 на 13

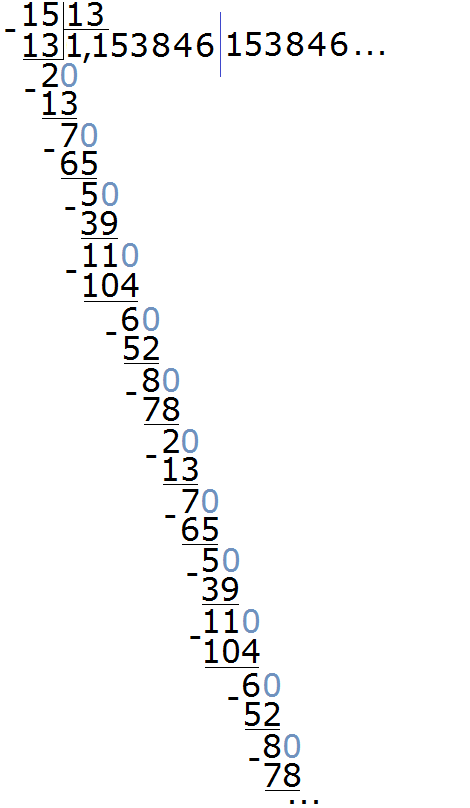
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:

Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».

Пример 4. Разделить 471 на 900

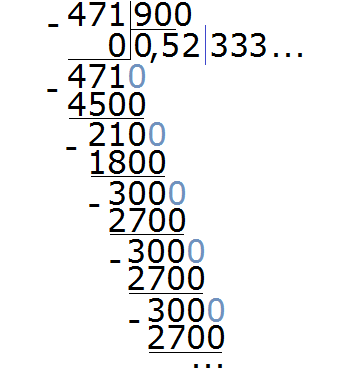
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:

Читается как: «ноль целых пятьдесят две сотых и три в периоде».

Десятичные дроби на координатном луче

Между точками и десятичными дробями существует взаимно однозначное соответствие.

Разберемся, как строятся точки на координатном луче, соответствующие данной десятичной дроби.

Конечные десятичные дроби и бесконечные периодические десятичные дроби мы можем заменить равными им обыкновенными дробями, после чего построить соответствующие . Например, десятичной дроби 1,4 отвечает обыкновенная дробь 14/10, поэтому точка с координатой 1,4 удалена от начала отсчета в положительном направлении на 14 отрезков, равных десятой доле единичного отрезка.

Десятичные дроби можно отмечать на координатном луче, отталкиваясь от разложения данной десятичной дроби по разрядам. Например, пусть нам нужно построить точку с координатой 16,3007, так как 16,3007=16+0,3+0,0007, то в данную точку можно попасть, последовательно откладывая от начала координат 16 единичных отрезков, 3 отрезка, длина которых равна десятой доле единичного, и 7 отрезков, длина которого равна десятитысячной доле единичного отрезка.

Такой способ построения десятичных чисел на координатном луче позволяет сколь угодно близко приблизиться к точке, отвечающей бесконечной десятичной дроби.

Иногда возможно точно построить точку, соответствующую бесконечной десятичной дроби. Например, , тогда этой бесконечной десятичной дроби 1,41421… соответствует точка координатного луча, удаленная от начала координат на длину диагонали квадрата со стороной 1 единичный отрезок.

Обратный процесс получения десятичной дроби, соответствующей данной точке на координатном луче, представляет собой так называемое десятичное измерение отрезка. Разберемся, как оно проводится.

Пусть наша задача заключается в том, чтобы попасть из начала отсчета в данную точку координатной прямой (или бесконечно приблизиться к ней, если попасть в нее не получается). При десятичном измерении отрезка мы можем последовательно откладывать от начала отсчета любое количество единичных отрезков, далее отрезков, длина которых равна десятой доле единичного, затем отрезков, длина которых равна сотой доле единичного, и т.д. Записывая количество отложенных отрезков каждой длины, мы получим десятичную дробь, соответствующую данной точке на координатном луче.

К примеру, чтобы попасть в точку М на приведенном выше рисунке, нужно отложить 1 единичный отрезок и 4 отрезка, длина которых равна десятой доле единичного. Таким образом, точке М соответствует десятичная дробь 1,4.

Понятно, что точкам координатного луча, в которые невозможно попасть в процессе десятичного измерения, соответствуют бесконечные десятичные дроби.

Список литературы.

• Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
• Математика. 6 класс : учеб. для общеобразоват. учреждений / . — 22-е изд., испр. — М.: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Перевод десятичных чисел в обыкновенную дробь

Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.

Представление дробей

Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:

• 0,5 = 1/2;
• 0,25 = 1/4;
• 1,375 = 11/8.

И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.

Избавляемся от запятой

Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:

Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.

Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:

• 0,5/1 = 5/10;
• 0,25/1 = 2,5/10 = 25/100;
• 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Шаг 3: Сокращаем полученные дроби до удобоваримого вида:

• 5/10 = 1 × 5 / 2 × 5 = 1/2;
• 25/100 = 1 × 25 / 4 × 25 = 1/4;
• 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.

Избавляемся от запятой еще проще

Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.

Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.

Шаг 2: Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:

• для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
• для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.

По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.

Шаг 3: Сокращаем нули и получаем итоговый результат:

• 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
• 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.

Преобразование на слух

Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.

0,025 = 25/1000 = 1/40

Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.

Примеры использования дробей в повседневной жизни

На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.

Работа

Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.

К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:

0,12 = 12/100 = 3/25

Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.

Округление результата преобразования простой дроби в десятичную

Следует заметить, что, в отличие от такого процесса, как преобразование десятичной дроби, эта процедура за частую может длиться бесконечно долго. В таких случаях говорят, что результат процедуры обращения обычной дроби в десятичную не может быть точным. Впрочем, практика показывает, что в подавляющем большинстве получение идеально точного результата и не требуется. Как правило, процесс деления заканчивается тогда, когда в его ходе уже получены значения тех десятичных долей, которые представляют в каждом конкретном случае практический интерес.

Пример 1

Требуется разрезать кусок масла весом один килограмм на девять одинаковых по своей массе частей. При выполнении этой процедуры оказывается, что масса каждой из них равняется / килограмма. Если по всем правилам осуществлять преобразование этой обычной дроби в дробь десятичную, то получится, что масса каждой из получившихся частей равняется ноль целых и один в периоде килограмма.

Определить массу совершенно точно не представляется возможным, поскольку деление можно осуществлять бесконечно. Для того чтобы его остановить, полученную величину просто округляют до какого-либо знака после запятой (как правило, до второго).

Округление ведется по стандартным правилам, предусмотренным в арифметике: если первая из «отбрасываемых» цифр имеет значение и более, то последняя из значимых увеличивается на единицу. В противном случае она остается неизменной.

Пример 2

Преобразовать обычную дробь одна восьмых в дробь десятичную.

Решение:

При делении единицы на восемь получается ноль целых сто двадцать пять тысячных или округлённо — ноль целых тринадцать сотых.

На практике преобразование десятичной дроби в простую и обратно подчиняется некоторым важным правилам целесообразности. К примеру, даже если тогда, когда простую можно обратить в десятичную абсолютно точно, но с большим количеством знаков после запятой, преобразование обычно заканчивают на некотором значимом для практических целей разряде.

Пример 3

Преобразовать обычную дробь девять тридцать вторых в дробь десятичную.

Решение:

Полезные советы и выводы

При переводе периодической десятичной дроби в обыкновенную, обратите внимание на количество цифр в периоде и корректно установите знаменатель.
Предварительное приведение десятичной дроби в неправильную поможет в выполнении вычислений и перевода в обыкновенную дробь.
Перевод чисел в дроби полезен при работе с десятичными дробями в математике и финансовых расчетах.

Теперь, с помощью представленных методов и примеров, вы сможете переводить десятичные периодические дроби в обыкновенную форму без особых трудностей.

Как представить обыкновенную дробь в виде десятичной и десятичную дробь в виде обыкновенной

Чтобы представить обыкновенную дробь в виде десятичной, необходимо записать цифры стоящие после запятой (десятичные знаки) в числитель и использовать знаменатель 1, с количеством нулей, равным количеству десятичных знаков. Затем, если возможно, можно сократить дробь. Если десятичные знаки начинаются с нулей, их не нужно писать в числитель обыкновенной дроби.

Чтобы представить десятичную дробь в виде обыкновенной, необходимо разделить числитель десятичной дроби на знаменатель, записать целую часть дроби и остаток в виде обыкновенной несократимой дроби. Если десятичная дробь имеет периодическую структуру, то она также может быть представлена в виде обыкновенной числовой дроби. Для этого нужно записать столько цифр периода, сколько необходимо, чтобы восстановить его исходную структуру, и затем произвести расчет.

Как перевести обыкновенную дробь в десятичную 1 3

Перевод обыкновенной дроби в десятичную систему может быть выполнен путем деления числителя на знаменатель. В данном случае, дробь 1/3 будет равна результату деления 1 на 3, то есть: 1/3 = 1:3 = 0,33333333333… . Здесь тройка повторяется бесконечное количество раз после запятой. Если необходимо представить десятичную дробь с ограниченным числом знаков после запятой, можно округлить результат. В данном случае, округление может быть выполнено следующим образом: 0,33333333333… ≈ 0,33 (при округлении до двух знаков после запятой). При таком округлении, получается десятичное приближение 1/3, а точное значение остается бесконечной в цепи троек после запятой.

Как делить десятичные дроби с целыми

Для деления десятичных дробей на целые числа существует несколько шагов. Первым шагом нужно разделить целую часть десятичной дроби на заданное целое число. Затем полученный частное записывается с запятой и далее продолжается деление до получения окончательного результата. Однако, если целая часть десятичной дроби меньше заданного делителя, то в частном пишется нуль целых, ставится запятая и деление завершается.

Как разделить обыкновенную дробь на десятичную дробь

Допустим, мы хотим разделить обыкновенную дробь 3/4 на десятичную дробь 0.5. Для этого нужно перенести запятые вправо на 1 цифру в обоих числах, получив 3 и 5. Затем мы можем просто разделить 3 на 5 и получить результат равный 0.6. Таким образом, десятичная дробь 0.5 равна обыкновенной дроби 3/4. Правило такое же для любых других дробей. Если у нас есть обыкновенная дробь, которую нужно разделить на десятичную дробь, мы переносим запятую вправо на столько цифр, сколько десятичных разрядов в делителе, затем выполняем деление на натуральное число. Это позволяет нам вычислить результат деления и получить соответствующую десятичную дробь.