Формула куба разности, куб суммы: как вычислить, разложение, примеры

Распределительный закон

Распределительный закон в математике – это формальное определение для свойства алгебраических операций, которое говорит о том, что произведение двух скобок равно сумме произведений каждого элемента в первой скобке с каждым элементом во второй скобке. Если проще, то можно умножать на число либо всю сумму, либо отдельно каждое слагаемое, и результат будет один и тот же.

Распределительный закон может быть описан формулой:

(a+b)c = ac + bc

А еще можете запомнить другие формулы распределительного закона:

ab + ac = a(b + c)
a(b + c) = ab + ac
ab – ac = a(b – c)
ab + ac + ad + … = a (b + c + d + …)

Давайте посмотрим на действие этого закона на примере.

Как мы помним, распределительный закон можно применить к следующему выражению:

a(b + c) = ab + ac

Здесь мы распределяем множитель «а» над слагаемыми «b» и «c» внутри скобок. Это означает, что мы умножаем «а» на «b» и «а» на «c» и получаем ab и ac соответственно. Например:

3(4 + 5) = 3 × 4 + 3 × 5 = 12 + 15 = 27

Также можно использовать распределительный закон наоборот, т.е. (a + b)c = ac + bc, и тогда мы получим:

(3 + 2)5 = 3 × 5 + 2 × 5 = 15 + 10 = 25

В обоих случаях результат совпадает, даже если мы распределили умножение до или после сложения.

Распределительный закон может быть применен и к сложным выражениям с несколькими скобками и сложными множителями. Например:

a(b + c + d) – e(f + g) = a(b + c + d) – ef – eg = ab + ac + ad – ef – eg

Здесь мы распределяем множитель «а» над слагаемыми «b», «c» и «d» внутри первых скобок, а множитель «e» над слагаемыми «f» и «g» внутри вторых скобок. Это означает, что мы умножаем «a» Начало формы

на «b», «a» на «c» и «a» на «d» и получаем ab, ac и ad соответственно. Также мы умножаем «e» на «f» и «e» на «g» и получаем ef и eg соответственно. Например:

2(3 + 4 + 5) – 3(2 + 1) = 2 × 3 + 2 × 4 + 2 × 5 – 3 × 2 – 3 × 1 = 6 + 8 + 10 – 6 – 3 = 15

В этом примере сначала мы раскрываем скобки и применяем распределительный закон, а затем складываем и вычитаем соответствующие члены, получая результат.

Важно отметить, что применение распределительного закона может помочь упростить и ускорить решение математических задач, но необходимо быть внимательными и тщательно проверять правильность решения, особенно в сложных выражениях

Применение формул сокращенного умножения

Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.

Примеры:

a2 + 2a + 1 = (a + 1)2
(aс − 4b)(ac + 4b) = a2c2 − 16b2

Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе
«Шпаргалки».

Ваши комментарии

Оставить комментарий:

15 ноября 2015 в 10:23

Кристина Костенко

ПрофильБлагодарили: Сообщений: 1

Кристина Костенко ПрофильБлагодарили: Сообщений: 1

(x+y+z)3=

Спасибо

Ответить

12 июня 2016 в 1:59Ответ для Кристина Костенко

Евгений Фёдоров

ПрофильБлагодарили: Сообщений: 60

Евгений Фёдоров ПрофильБлагодарили: Сообщений: 60

Перемножить тупо лень?

Спасибо

Ответить

6 сентября 2015 в 19:02

Артур Хорішко

ПрофильБлагодарили: Сообщений: 1

Артур Хорішко ПрофильБлагодарили: Сообщений: 1

(3ч-4)в квадрате=0,25

Спасибо

Ответить

2 сентября 2016 в 15:41Ответ для Артур Хорішко

Евгений Колосов

ПрофильБлагодарили: 12 Сообщений: 197

Евгений Колосов ПрофильБлагодарили: 12 Сообщений: 197

полагаю, что имеется ввиду пример:
(3 · x ?4)2=0,25
Применим формулу «разность квадратов» и решим квадратное уравнение, найдя корни.
9 · x2 ? 2 · 3 · 4 · x + 16 = 0,25
9×2-24x+15,75=0
D=9
x₁=1,5
x₂=1

Произведем проверку подставив в исходное выражение каждый из получившихся корней:
1) (3 · 1,5 ?4)2=0,25
0,52=0,25
2) (3 ·

?4)2=0,25
-0,52=0,25

Спасибо

Ответить

Разложение суммы кубов

Посмотрим, как можно разложить суммированные кубы. Запишем еще раз полученную формулу:

$(a+b)^3 = a^3+3a^2 b+3ab^2+b^3$

Вычислим с ее помощью сумму пары кубов:

$a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) = (a+b)(a^2-ab+b^2 )$

Рассмотрим следующий многочлен:

$(a^2-ab+b^2 )$

Данное выражение носит название неполного квадрата разности и имеет знак минуса. Для понимания запишем соотношение полного квадрата разности, которое имеет следующий вид:

$(a^2-2ab+b^2 ) = (a-b)^2$

В результате получилось соотношение, подходящее для упрощения задачи по разложению суммы пары кубов на несколько множителей:

$a^3+b^3 = (a+b)(a^2-ab+b^2 )$

Кубы пары выражений в сумме дают произведение суммы данных выражений и неполного квадрата разности этих же выражений, то есть:

$a^3+b^3 = (a+b)(a^2-ab+b^2 )$

Формула суммы кубов

В алгебре существуют специальные формулы, с помощью которых удается значительно сократить последовательные расчеты при перемножении одночленов и многочленов с цифрами или буквами. Данные принципы применяют в решении разнообразных задач. Это особый случай уравнения бинома Ньютона. Как правило, использование таких формул изучают на уроках в средних классах школы.

Популярные методы упрощения действия умножения применимы в каждом из математических разделов, в том числе, элементарной алгебре и высшей математике. С помощью достаточно простых закономерностей из сложных выражений получают простые соотношения, находят корни разных уравнений и неравенств, записывают в сокращенной версии дробные числа, высчитывают пределы и интегралы. Рассмотрим одну из формул сокращенного умножения под названием сумма кубов.

Сумма кубов пары выражений вычисляется, как результат умножения суммы данных выражений и неполного квадрата разности этих же выражений, то есть:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

$a^{3} + b^{3} = (a + b) \cdot (a^{2} — ab + b^{2})$

Попробуем доказать записанное равенство. С этой целью выполним умножение выражений, заключенных в скобки, путем устранения этих скобок. Таким образом:

$(a + b) \cdot (a^{2} — ab + b^{2}) = a^{3} — a^{2}b + ab^{2} + ba^{2} — ab^{2} + b^{3} = a^{3} + b^{3}$

В результате формула сокращенного умножения, то есть в данном случае сумма кубов, доказана.

В распространенных ситуациях рассмотренное выше соотношение используют при решении задач в алгебре, когда требуется:

разложить выражение на множители;
упростить решаемый пример.

Примеры использования формул

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Пример (x + 3y) 2 = x 2 + 2 ·x·3y + (3y) 2 = x 2 + 6xy + 9y 2

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Пример: (4x –y) 2 = (4x) 2 -2·4x·y + y 2 = 16x 2 — 8xy + y 2

Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

Пример: 9x 2 – 16y 2 = (3x) 2 – (4y) 2 = (3x – 4y)(3x + 4y)

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a+b) 3 = a 3 +3a 2 b+3ab 2 +b 3

Пример: (x + 2y) 3 = x 3 + 3·x 2 ·2y + 3·x·(2y) 2 + (2n) 3 = x 3 + 6x 2 y + 12xy 2 + 8y 3

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b) 3 = a 3 — 3a 2 b+3ab 2 -b 3

Пример: (2x – y) 3 = (2x) 3 -3·(2x) 2 ·y + 3·2x·y 2 – y 3 = 8x 3 – 12x 2 y + 6xy 2 – y 3

Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

Пример: 125 + 8y 3 = 5 3 + (2y) 3 = (5 + 2y)(5 2 — 5·2y + (2y) 2 ) = (5 + 2y)(25 – 10y + 4y 2 )

Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

Пример: 64x 3 – 8 = (4x) 3 – 2 3 = (4x – 2)((4x) 2 + 4x·2 + 2 2 ) = (4x – 2)(16x 2 + 8x + 4)

Решение примеров на все формулы сокращенного умножения

Упростить выражение

\displaystyle \frac{4a^2+4ab+4b^2}{5a+5b} \cdot \frac{3a^2-3b^2}{6a^3-6b^3}

Решение:

Вынесем в каждом дроби и в числителе, и в знаменателе за скобки общий множитель:

\displaystyle \frac{4a^2+4ab+4b^2}{5a+5b} \cdot \frac{3a^2-3b^2}{6a^3-6b^3}=\frac{4 (a^2+ab+b^2)}{5 (a+b)} \cdot \frac{3 (a^2-b^2)}{6 (a^3-b^3)}

Используя формулы разности квадратов и разности кубов двух выражений, получим:

\displaystyle \frac{4 (a^2+ab+b^2)\cdot 3 (a^2-b^2)}{5 (a+b)\cdot 6 (a^3-b^3)}=\frac{4 (a^2+ab+b^2)\cdot 3 (a-b)(a+b)}{5 (a+b)\cdot 6 (a-b)(a^2+ab+b^2)}

Сокращаем дробь

\displaystyle \frac{4\red{\bcancel{(a^2+ab+b^2)}}\cdot 3 \green{\bcancel{(a-b)}}\bcancel{(a+b)}}{5\bcancel{(a+b)}\cdot 6\green{\bcancel{(a-b)}}\red{\bcancel{(a^2+ab+b^2)}}}=\frac{12}{30}=\frac{2}{5}

Ответ: \displaystyle \frac{2}{5}

Выполнить действия

\displaystyle 2m-\left (\frac{2m-3}{m+1}-\frac{m+1}{2-2m}-\frac{m^2+3}{2m^2-2}\right)\frac{m^3+1}{m^2-m}

Решение:

Выполним сначала действия в скобках

\displaystyle \frac{2m-3}{m+1}-\frac{m+1}{2-2m}-\frac{m^2+3}{2m^2-2}=\frac{2m-3}{m+1}-\frac{m+1}{2-2m}-\frac{m^2+3}{2m^2-2}=\frac{2m-4}{m+1}-\frac{m+1}{2 (1-m)}-\frac{m^2+3}{2 (m^2-1)}=\displaystyle \frac{2m-3}{m+1}+\frac{m+1}{2 (m-1)}-\frac{m^2+3}{2 (m^2-1)}=\frac{2 (2m-3)(m-1)+(m+1)(m+1) — (m^2+3)}{2 (m^2-1)}=\displaystyle \frac{4m^2-6m-4m+6+m^2+2m+2m+1-m^2-3}{2 (m^2-1)}=\frac{4m^2-8m+4}{2 (m^2-1)}=\frac{4 (m-1)^2}{2 (m-1)(m+1)}=\frac{2 (m-1)}{m+1}

Выполним умножение:

\displaystyle \frac{2 (m-1)}{m+1} \cdot \frac{m^3+1}{m^2-m}=\frac{2 (m-1)(m+1)(m^2-m+1)}{(m+1) m (m-1)}=\frac{2 (m^2-m+1)}{m}

И, далее:

\displaystyle 2m-\frac{2 (m^2-m+1)}{m}=\frac{2 (m^2- (m^2-m+1))}{m}=\frac{2 (m^2-m^2+m-1)}{m}=\frac{2 (m-1)}{m}

Ответ: \displaystyle \frac{2 (m-1)}{m}

Разность квадратов,

Пример задач на использование формул разности квадратов и суммы и разности кубов

Пример 4

Разложить на множители.

а) ${(a+5)}^2-9$

в) $-x^3+\frac{1}{27}$

Решение:

а) ${(a+5)}^2-9$

Применяя формулу разности квадратов, получим:

Запишем данное выражение в виде:

Применим формулу кумы кубов:

в) $-x^3+\frac{1}{27}$

Запишем данное выражение в виде:

Применим формулу кумы кубов:

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого. В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример.
Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

Разность кубов

Формула разности кубов отличается от суммы кубов лишь одним знаком. Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).

Пример.
Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.

Если значения сторон небольшие, то вычисления довольно просты. А если длины сторон выражаются в значительных числах, то стоит применить формулу, озаглавленную «Разность кубов» (или «Куб разности»), которае значительно упростит вычисления.

Доказательство формул сокращенного умножения

Помните, что разность квадратов двух чисел a и b равна произведению их разности на их сумму: a2 — b2 = (a — b) * (a + b).

Другими словами, произведение суммы а и b на их разность равно разности их квадратов: (а — b) * (а + b) = а2 — b2.

Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2. Докажем, что a2 — b2 = (a — b) * (a + b)

Докажем, что a2 — b2 = (a — b) * (a + b).

Идти:

Искусственным методом сложим и вычтем одно и то же a * b.+ а * б — а * б = 0
а2 — Ь2 = а2 — Ь2 + аб — аб

Сгруппируйте по-разному: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
Продолжим группировку: a2 — a * b — b2 + a * b = (a2 — a * b) + (a * b — b2)
Вынесем общие множители за скобки:(a2 — a * b) + (a * b — b2) = a * (a — b) + b * (a — b)

Вынесем за скобки (a — b) a * (a — b) + b * (a — b) = (a — b) * (a + b)
Результат доказательства: a2 — b2 = (a — b) * (a + b)
Чтобы доказать в обратном направлении: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — б * а — б * б = а2 — б2.

Аналогичным методом можно доказать остальные ФСО.

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b)2 = a2 − 2ab + b2

Эту формулу можно прочитать так:

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)

(a − b)2 = (a − b)(a − b)

Если выполнить это умножение, то получится многочлен a2 − 2ab + b2

(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2

Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49×2 − 70x + 25

Значит, (7x − 5)2 = 49×2 − 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5)2 = (7x − 5)(7x − 5) = 49×2 − 35x − 35x + 25 = 49×2 − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

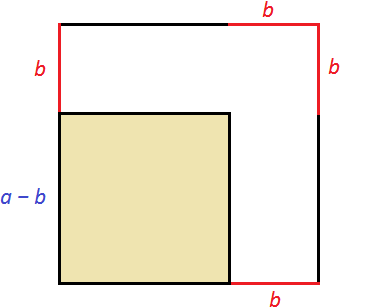
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

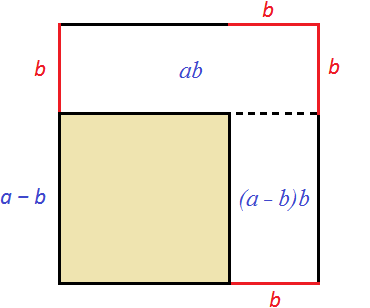
Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b

a2 − ab − (a − b)b

Раскроем скобки в выражении (a − b)b

a2 − ab − ab + b2

Приведем подобные слагаемые:

a2 − 2ab + b2

В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:

(a − b)2 = a2 − 2ab + b2

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.

(5x − 2y)2a = 5xb = 2y(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25×2 − 20xy + 4y2

Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y)2 = (5x + (−2y))2

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y)2a = 5xb = −2y(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25×2 − 20xy + 4y2

Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)

(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2

Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y)2 = x2 + 2xy + y2

Практическое применение формул сокращенно умножения, особенности преподавания в школе

В современной системе образования преобладает системно-деятельностный подход. Это означает, что инициатива к поглощению знаний должна исходить от ученика, а учителю следует только направлять его в нужном направлении. У многих учащихся отсутствует интерес к учёбе, они ссылаются на то, что эти знания нигде не пригодятся в жизни. Как быть учителю в данной ситуации? Какие способы мотивации изучения формул сокращенного умножения найти? Эти замечательные формулы еще как пригодятся в житейских ситуациях. В частности, при подборе строительного материала для дома. Например, вы пришли в супермаркет, и продавец по размеру пола (106 м) навязывает 13 000 м2 паркетной доски. Зная ФСУ, вы с лёгкостью в уме сможете проверить, не обманывает ли вас работник магазина.

(106 м)2=(100+6) 2=10 000+2*100*6+36= 11236 м2

Оказывается, вам достаточно будет 11236 м2.

Многие учащиеся ссылаются еще и на то, что сложно выучить и запомнить все эти семь формул. Если, вы умеете перемножать выражения, то ничего заучивать и не придётся. Известно, что а3=а*а*а. то есть, нужно умножить число или выражение само на себя столько раз, сколько написано в показателе степени.

Рассмотрим выведение формулы куб суммы:

И так можно вывести абсолютно любую формулу. Главное, уметь упрощать выражения, умножать, приводить подобные слагаемые. Кроме аналитического доказательства формул сокращенного умножения, имеет место быть еще и геометрический. О нём нельзя не упомянуть на уроках алгебры. Полезно будет дать это задание в качестве домашнего в рамках исследовательской деятельности учащихся.

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.

Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)2 = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4×2 + 6xy + 6xy + 9y2 = 4×2 + 12xy + 9y2

То есть выражение (2x + 3y)2 равно 4×2 + 12xy + 9y2

(2x + 3y)2 = 4×2 + 12xy + 9y2

Решим аналогичный пример, который попроще:

(a + b)2

Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)2 = (a + b)(a + b)

Выполним это умножение:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2

То есть выражение (a + b)2 равно a2 + 2ab + b2

(a + b)2 = a2 + 2ab + b2

Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4×2 + 12xy + 9y2

Как и в прошлый раз получили многочлен 4×2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)2 = 4×2 + 12xy + 9y2

Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)2 = 52 = 25

Второй способ:

(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9

Значит, (5a + 3)2 = 25a2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

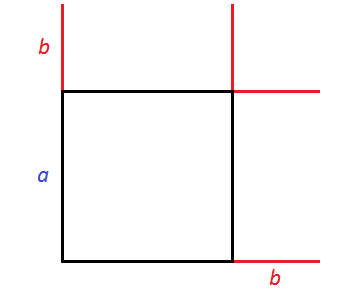
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

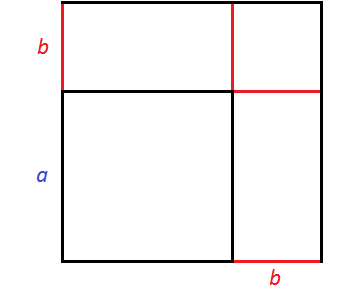
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

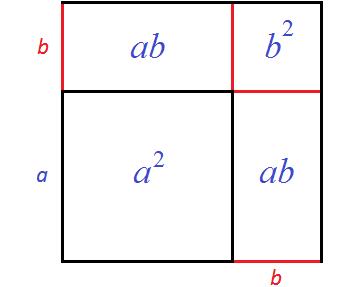
В результате получается следующая сумма площадей:

a2 + ab + ab + b2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Как читать формулы сокращенного умножения

Научитесь произносить формулы сокращенного выражения:

Разность между квадратами двух выражений равна произведению их разности на их сумму.
Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого и второго плюс квадрат второго.
Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого и второго плюс квадрат второго.
Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
Разность кубов двух выражений равна произведению разности первого и второго выражений на неполный квадрат их суммы.
Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второй.
Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого и второго плюс утроенное произведение первого на квадрат второго минус куб второго.

Формулы сокращенного умножения

Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или, скажем, квадрата суммы, просто невозможно.

Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,162 — 2 • 3,16 • 1,16 + 1,162.

Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!

Итак, семь формул «школьной» алгебры, которые должны знать все:

Название	Формула
Квадрат суммы	(A + B)2 = A2 + 2AB + B2
Квадрат разности	(A — B)2 = A2 — 2AB + B2
Разность квадратов	(A — B)(A + B) = A2 — B2
Куб суммы	(A + B)3 = A3 + 3A2B + 3AB2+ B3
Куб разности	(A — B)3 = A3 — 3A2B + 3AB2 — B3
Сумма кубов	A3 + B3 = (A + B)(A2 — AB + B2)
Разность кубов	A3 — B3 = (A — B)(A2 + AB + B2)

Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко. Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии

Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает)

Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).

Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.

Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?

Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона.

Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:

(A + B)n = An + Cn1An-1B + Cn2An-2B2 + … + CnkAn-kBk + … + Bn.

Здесь Cnk = n!/(k! • (n-k)!).

Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!

Да, можно. Вот эта формула:

An — Bn = (A — В)(An-1 + An-2B + An-3B2 + … + Bn-1).

Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:

An + Bn = (A + В)(An-1 — An-2B + An-3B2 — … + Bn-1).

Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.