Примеры способа формулы сокращенного умножения

Применение ФСУ для решения уравнений

К примеру, нужно решить уравнение, содержащее многочлен 3 степени:

x³ + 3x² + 3x + 1 = 0.

В школьной программе не рассматриваются универсальные приёмы для решения кубических уравнений, и подобные задания чаще всего решаются более простыми методами (например, разложением на множители). Если заметить, что левая часть тождества напоминает куб суммы, то уравнение можно записать в более простом виде:

(x + 1)³ = 0.

Корень такого уравнения вычисляется устно: x = -1.

Аналогичным способом решаются неравенства. Для примера можно решить неравенство x³ 6x² + 9x &gt, 0.

В первую очередь необходимо разложить выражение на множители. Вначале нужно вынести за скобку x

После этого следует обратить внимание, что выражение в скобках можно преобразовать в квадрат разности

Затем необходимо найти точки, в которых выражение принимает нулевые значения, и отметить их на числовой прямой. В конкретном случае это будут 0 и 3. Затем методом интервалов определить, в каких промежутках x будет соответствовать условию неравенства.

ФСУ могут оказаться полезными при выполнении некоторых расчётов без помощи калькулятора:

703² 203² = (703 + 203)(703 — 203) = 906 ∙ 500 = 453000.

Решение сложных задач

\

Рассмотрим каждое слагаемое отдельно.

Первая дробь:

\

\

\

\

Вторая:

\

\

\

Весь числитель второй дроби мы можем переписать следующим образом:

\

Теперь посмотрим на знаменатель:

\

Давайте перепишем все рациональное выражение с учетом вышеизложенных фактов:

\

\

Ответ: $\frac{\left( 3a-4b \right)\left( b+2 \right)}{\left( b-2 \right)}$.

Нюансы решения

Как мы еще раз убедились, неполные квадраты суммы либо неполные квадраты разности, которые часто встречаются в реальных рациональных выражениях, однако не стоит их пугаться, потому что после преобразования каждого элемента они практически всегда сокращаются. Кроме того, ни в коем случае не стоит бояться больших конструкций в итогом ответе — вполне возможно, что это не ваша ошибка (особенно, если все разложено на множители), а это автор задумал такой ответ.

В заключение хотелось бы разобрать еще один сложных пример, который уже не относится напрямую к рациональным дробям, однако он содержит все то, что ждет вас на настоящих контрольных и экзаменах, а именно: разложение на множители, приведение к общему знаменателю, сокращение подобных слагаемых. Вот именно этим мы сейчас и займемся.

Фсу – формулы сокращённого умножения по алгебре за 7 класс с примерами

Основная задача формул сокращённого умножения

Формулы сокращённого умножения (ФСУ) нужны для того, чтобы умножать и возводить в степень числа, выражения, в том числе многочлены. То есть, при помощи формул можно работать с числами значительно быстрее и проще. Таким образом можно из сложного уравнения сделать обычное, что упростит задачу.

Таблица с формулами сокращённого умножения

Квадрат суммы		Квадрат первого выражения плюс удвоенного произведение первого и второго выражения, плюс квадрат второго выражения.
Квадрат разности		Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.
Куб суммы		Куб разности двух выражений равен кубу первого выражения плюс утроенное произведение первого выражения в квадрате на второе выражение, плюс утроенное произведение первого выражения на второе в квадрате, плюс второе выражение в кубе.
Куб разности		Куб разности двух величин равен первое выражение в кубе минус утроенное произведение первого выражения в квадрате на второе выражение, плюс утроенное произведение первого выражения на второе в квадрате, минус второе выражение в кубе.
Разность квадратов		Разность квадратов первого и второго выражений равен произведению разности двух выражений и их суммы.
Сумма кубов		Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
Разность кубов		Произведение разности двух выражений на неполный квадрат суммы равно разности их кубов.

Формулы сокращенного умножения (скачать таблицу для печати)

Обратите внимание на первые четыре формулы. Благодаря им можно возводить в квадрат или куб суммы (разности) двух выражений

Что касается пятой формулы, её нужно применять, чтобы вкратце умножить разность или сумму двух выражений.

Две последние формулы (6 и 7) применяются, чтобы умножать суммы обоих выражений на их неполный квадрат разности или суммы.

Вышеперечисленные формулы довольно-таки часто нужны на практике. Именно поэтому их желательно знать наизусть.

Если вам попался пример, разложить многочлен на множители, тогда во многих случаях нужно левую и правую часть переставить местами.

Такую же процедуру можно проделывать и с остальными формулами.

Доказательство ФСУ

Шаг первый.

Возведём a + b во вторую степень. Для этого степень трогать не будем, а выполним банальное умножение:  = x .

Шаг второй. Теперь и выносим за скобки: x + x .

Шаг третий. Раскрываем скобки: x + x + x + x .

Шаг четвёртый. Умножаем, не забывая о знаках: x + x + .

Шаг пятый. Упрощаем выражение: .

Точно так же можно доказать абсолютно любую формулу сокращённого умножения.

Примеры и решения с помощью ФСУ

Как правило, эти семь формул применяются тогда, когда нужно упростить выражение, чтобы решить какое-либо уравнение и даже обычный пример.

Пример 1

• Задание
• Упростите выражение:
• Как видно, к этому примеру подходит первая формула сокращённого умножения – Квадрат суммы.
• Решение

Исходя из первой формулы надо пример разложить на множители. Для этого смотрим на формулу и вместо букв подставляем цифры. В нашем случае «а» – это 3x, а «b» – это 5:

1. x x +
2. Считаем правую часть и записываем результат. У нас получается:
3. + x x +
4. В примере надо умножить всё то, что умножается и сразу получаем ответ:

Конечно же, есть примеры и с дробями. Но, если научитесь решать простые примеры, тогда другие виды вам будут не страшны.

Пример 2

• Задание
• Упростите выражение
• Решение
• = – x x + =

Пример 3

1. Задание
2. Представьте в виде квадрата двучлена трёхчлен
3. Решение
4. Здесь квадраты выражений – и
5. Выражения, которые возводились в квадрат – и
6. Удвоенное произведение этих выражений – , который совпадает с со вторым членом трёхчлена (со знаком «плюс), значит,

Итак, как видно, ничего сложно в примерах нет. Главное, знать формулы, где их можно применять, а где можно обойтись и без них.

Полезные источники

1. Арефьева И. Г., Пирютко О. Н. Алгебра: учебник пособие для 7 класса учреждений общего среднего образования: Минск “Народная Асвета”, 2017 – 304 с.
2. Никольский С. М., Потапов М. К. Алгебра 7 класс: М: 2015 – 287 с.
3. Рубин А. Г., Чулков П. В. Алгебра. 7 класс. М: 2015 – 224 с.

Примеры использования формул сокращенного умножения

Как уже было сказано, формулы сокращенного умножения позволяют быстро и кратко возвести выражение в степень. ФСУ применяются еще и при сокращении дробей и выражений, разложении многочленов на множители, вычислении интегралов и пределов. Рассмотрим примеры формулы сокращенного умножения. Эти примеры содержат уже готовые формулы сокращенного умножения и ответы.

Пример 1. Преобразовать выражение \ в многочлен стандартного вида. Раскроем скобки, используя формулу квадрата суммы, и приведем подобные слагаемые. \

Пример 2. Разложить на множители \.

Используем формулу степеней и применим формулу разности квадратов: \

Пример 3. Сократить дробь, при этом используйте формулы сокращенногоСнимок экрана от 2021-12-14 14-48-10 умножения \

Заметим, что выражение, представленное в числителе, является разностью квадратов формул сокращенного умножения. Применим её и сократим на идентичные выражения в числителе и знаменателе (х-3):

\

Пример 4. Упростить выражение \ и найти его значение при \

Раскрываем скобки: \

Теперь можно подставить в выражение значение переменной а.

\

Пример 5. Вычислить \

Числа 63 и 57 можно представить в виде суммы и разности двух одинаковых чисел. Следовательно, для вычисления произведения \ удобно использовать формулу разности квадратов. Данное вычисление можно посчитать устно.

\

Пример 6. Раскрыть скобки \

Возведем в квадрат.

\

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.

Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)2 = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4×2 + 6xy + 6xy + 9y2 = 4×2 + 12xy + 9y2

То есть выражение (2x + 3y)2 равно 4×2 + 12xy + 9y2

(2x + 3y)2 = 4×2 + 12xy + 9y2

Решим аналогичный пример, который попроще:

(a + b)2

Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)2 = (a + b)(a + b)

Выполним это умножение:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2

То есть выражение (a + b)2 равно a2 + 2ab + b2

(a + b)2 = a2 + 2ab + b2

Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4×2 + 12xy + 9y2

Как и в прошлый раз получили многочлен 4×2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)2 = 4×2 + 12xy + 9y2

Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)2 = 52 = 25

Второй способ:

(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9

Значит, (5a + 3)2 = 25a2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

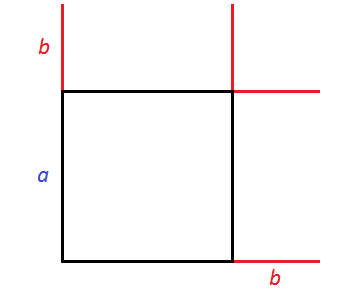
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

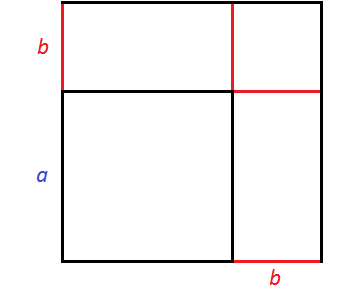
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

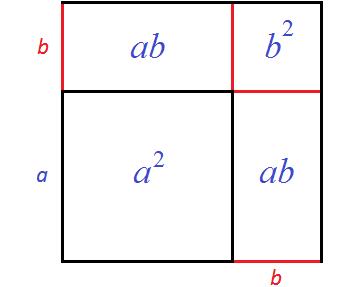
В результате получается следующая сумма площадей:

a2 + ab + ab + b2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Применение формул сокращенного умножения

Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.

• a2 + 2a + 1 = (a + 1)2
• (aс − 4b)(ac + 4b) = a2c2 − 16b2

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители:

вынесение общего множителя за скобки и

способ группировки.

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула разности кубов.

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в. (a − b)(a2 ab + b2) = a3 − b3

(a − b)(a2 ab + b2) = a3 − b3

Как разложить на множители разность кубов

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «» — это «», значит, для формулы разности кубов вместо «» мы используем «». Используем формулу разности кубов

На месте «» у нас стоит «», а на месте «», как и в формуле, стоит «»

Используем формулу разности кубов. На месте «» у нас стоит «», а на месте «», как и в формуле, стоит «».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x2 + x + 1)» напоминает правую часть формулы разности кубов

«a3 − b3 = (a − b)(a2 ab + b2)», только вместо «» стоит «», а на месте «» стоит «».

Используем для «(x − 1)(x2 + x + 1)» формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y2 − 1)(y4 + y2 + 1)» с правой частью формулы разности кубов «a3 − b3 = (a − b)(a2 ab + b2)», то можно понять, что на месте «» из первой скобки стоит «, а на месте «» стоит «».

Одночлены, которые стоят на месте «» или «» могут стоять в степени.

Например, в рассматриваемом примере на месте «» стоит «». Это означает, что именно «» мы рассматриваем как «».

Представим скобку «(y4 + y2 + 1)» таким образом, чтобы она соответствовала правой части формулы разности кубов.

Используем формулу разности кубов и решим пример до конца.

Вспомним, как выглядит формула суммы кубов.

a3 + b3 = (a + b)(a2 ab + b2)

Формула суммы кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

(a + b)(a2 ab + b2) = a3 + b3

Как разложить на множители сумму кубов

Рассмотрим пример. Необходимо разложить на множители сумму кубов.

Обратим внимание, что «» — это «», значит, для формулы суммы кубов вместо «» мы используем «». Используем формулу суммы кубов

Только вместо «» у нас будет «», а вместо «» будет «»

Используем формулу суммы кубов. Только вместо «» у нас будет «», а вместо «» будет «».

Применение суммы кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в сумму кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(p + 1)(p2 − p + 1)» напоминает правую часть формулы суммы кубов

«a3 + b3 = (a + b)(a2 ab + b2)», только вместо «» стоит «», а на месте «» стоит «».

Используем для произведения многочленов «(p + 1)(p2 − p + 1)» формулу сумму кубов в обратную сторону.

В этом произведении многочленов не так очевидно, что будет являться в формуле «», а что «».

Если сравнить «(2a + 3)(4a2 − 6a + 9)» с формулы суммы кубов «a3 + b3 = (a + b)(a2 ab + b2), то можно понять, что в первой скобке «(2a + 3)» на месте «» стоит «», а на месте «» стоит «».

Теперь представим скобку «(4a2 − 6a + 9)» таким образом, чтобы она соответствовала правой части формулы суммы кубов.

Используем формулу суммы кубов и решим пример до конца.

В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, разложение разности кубов на множители. Также разберем примеры решения задач для закрепления представленного материала.

Доказательство формул сокращенного умножения

1. \( {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\).Возвести выражение в квадрат — значит умножить его само на себя:\( {{\left( a+b \right)}^{2}}=\left( a+b \right)\left( a+b \right)\).Раскроем скобки и приведем подобные:

\( {{\left( a+b \right)}^{2}}=\left( a+b \right)\left( a+b \right)={{a}^{2}}+\underline{ab}+\underline{ba}+{{b}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\).2. \( {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\).Делаем то же самое: умножаем разность саму на себя, раскрываем скобки и приводим подобные:\( {{\left( a-b \right)}^{2}}=\left( a-b \right)\left( a-b \right)={{a}^{2}}-\underline{ab}-\underline{ba}+{{b}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\).

3. \( {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\).Возьмем выражение в правой части и раскроем скобки:\( \left( a-b \right)\left( a+b \right)={{a}^{2}}+\underline{ab}-\underline{ba}-{{b}^{2}}={{a}^{2}}-{{b}^{2}}\).

4. \( {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\).Число в кубе можно представить как это число умноженное на свой квадрат:\( \displaystyle {{\left( a+b \right)}^{3}}={{\left( a+b \right)}^{2}}\cdot \left( a+b \right)=\underbrace{\left( {{a}^{2}}+2ab+{{b}^{2}} \right)}_{квадрат\ суммы}\left( a+b \right)=\)\( \displaystyle={{a}^{3}}+\underline{{{a}^{2}}b}+\underline{2{{a}^{2}}b}+\underline{\underline{2a{{b}^{2}}}}+\underline{\underline{{{b}^{2}}a}}+{{b}^{3}}=\)\( \displaystyle={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\)5. \( \displaystyle {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\)Аналогично:\( \displaystyle {{\left( a-b \right)}^{3}}={{\left( a-b \right)}^{2}}\cdot \left( a-b \right)=\underbrace{\left( {{a}^{2}}-2ab+{{b}^{2}} \right)}_{\text{квадрат}\ \ разности}\left( a-b \right)=\)\( \displaystyle {{a}^{3}}-\underline{{{a}^{2}}b}-\underline{2{{a}^{2}}b}+\underline{\underline{2a{{b}^{2}}}}+\underline{\underline{{{b}^{2}}a}}-{{b}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\)В разности кубов знаки чередуются.6. \( {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\).Раскроем скобки в правой части:\( \left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)={{a}^{3}}-\underline{{{a}^{2}}b}+\underline{\underline{a{{b}^{2}}}}+\underline{{{a}^{2}}b}-\underline{\underline{a{{b}^{2}}}}+{{b}^{3}}={{a}^{3}}+{{b}^{3}}\).

Разность и сумма кубов

Рассмотрим последнюю пару формул разность и сумму кубов.

Как мы помним, в разности квадратов у нас идет перемножение разности и суммы данных чисел одно на другое. В разности кубов и в сумме кубов также имеется две скобки:

\( {{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\);

\( {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\).

1 скобка – разность (или сумма) чисел в первой степени (в зависимости от того, разность или сумму кубов мы раскрываем);

2 скобка – неполный квадрат (присмотрись: если бы мы вычитали (или прибавляли) удвоенное произведение чисел, был бы квадрат), знак при перемножении чисел противоположный знаку изначального выражения.

Примеры задач

Задача 1

Дано несколько выражений, которые с применением формул сокращенного умножения требуется разложить на множители:

\(x^3+y^3\)

\(m^3-n^3\)

\(8a^3+1\)

\(125-64y^3\)

\(\frac{1}{8} k^6-8\)

\(27+ \frac{m^3}{125}\)

Решение

Вспомним правило куба суммы и выполним соответствующие преобразования. В результате:

\(x^3+y^3 = (x+y)(x^2-xy+y^2)\)

\(m^3-n^3 = (m-n)(m^2+mn+n^2)\)

\(8a^3+1 = (2a)^3+1^3 = (2a+1)(4a^2-2a+1)\)

\(125-64y^3 = 5^3-(4y)^3 = (5-4y)(25+20y+16y^2)\)

\(\frac{1}{8} k^6-8 = ( \frac{1}{2} k^2 )^3-2^3=(\frac{1}{2} k^2-2)(\frac{1}{4} k^4+k^2+4)\)

\(27+ \frac{m^3}{125} = 3^3+(\frac{m}{5})^3 = (3+\frac{m}{5})(9-\frac{3m}{5}+\frac{m^2}{25})\)

Ответ: \((x+y)(x^2-xy+y^2); (m-n)(m^2+mn+n^2); (2a+1)(4a^2-2a+1); (5-4y)(25+20y+16y^2); (\frac{1}{2} k^2-2)(\frac{1}{4} k^4+k^2+4); (3+\frac{m}{5})(9-\frac{3m}{5}+\frac{m^2}{25}).\)

Задача 2

 Дано следующее выражение:

\(19^3-11^3\)

Необходимо представить доказательства его кратности числу 8.

Решение

Воспользуемся формулой разности кубов, которую достаточно просто получить из соотношения суммы кубов. Выполним преобразования путем деления данного выражения на число 8:

\(\frac{19^3-11^3}{8} = \frac{(19-11)(19^2+19\cdot11+11^2 )}{8} = \frac{8(19^2+19\cdot11+11^2 )}{8} = 19 ^2+19\cdot11+11^2\)

Ответ: выражение \(19^3-11^3\) кратно числу 8.

Задача 3

Дано несколько выражений, которые с помощью применения формул сокращенного умножения требуется записать в форме многочлена:

\((x+5)^3\)

\((9-z)^3\)

\((5b-3c)^3\)

\((2mk+1)^3\)

Решение

Выполним соответствующие преобразования, используя уже знакомые правила разложения кубов суммы и разности кубов на многочлены:

\((x+5)^3 = x^3+3\cdot x^2\cdot5+3\cdot x\cdot5^2+5^3 = x^3+15x^2+75x+125\)

\((9-z)^3 = 9^3-3\cdot9^2\cdot z+3\cdot9\cdot z^2-z^3 = 729-243+27z^2-z^3\)

\((5b-3c)^3 = (5b)^3-3\cdot(5b)^2\cdot3c+3\cdot5b\cdot(3c)^2-(3c)^3 = 125b^3-225b^2c+135bc^2-27c^3\)

\((2mk+1)^3 = (2mk)^3+3\cdot(2mk)^2\cdot1+3\cdot2mk\cdot1^2+1^3 = 8m^3k^3+12m^2k^2+6mk+1\)

Ответ:  \(x^3+15x^2+75x+125; 729-243+27z^2-z^3; 125b^3-225b^2 c+135bc^2-27c^3; 8m^3k^3+12m^2k^2+6mk+1.\)

Задача 4

Необходимо записать в упрощенной форме следующие выражения:

\((a+2)^3-(a-2)^3\)

\((x-3y)^3+9xy(x-3y)\)

\((x+y)^3-x(x-y)^2\)

\(3m(k+3m)^2-(k+3m)^3\)

Решение

Заметим, что в данном случае целесообразно воспользоваться формулами сокращенного умножения. Применим куб суммы и куб разности, чтобы упростить соотношения и запишем ответы:

\((a+2)^3-(a-2)^3 = a^3+3a^2\cdot2+3a\cdot2^2+2^3-(a^3-3a^2\cdot2+3a\cdot2^2-2^3 )= 2\cdot6a^2-2\cdot8 = 12a^2-16\)

\((x-3y)^3+9xy(x-3y) = x^3-3x^2\cdot3y+3x\cdot(3y)^2-27y^3+9x^2 y-27xy^2 = x^3-27y^3\)

\((x+y)^3-x(x-y)^2 = x^3-3x^2 y+3xy^2+y^3-x(x^2-2xy+y^2 ) = x^3-3x^2 y+3xy^2+y^3-x^3+2x^2 y-xy^2 = -x^2 y+2xy^2+y^3\)

\(3m(k+3m)^2-(k+3m)^3 = 3m(k^2+6km+9m^2 )-(k^3+3k^2\cdot3m+3k\cdot(3m)^2+(3m)^3 ) = 3k^2 m+18km^2+27m^3- k^3-9k^2 m-27km^2-27m^3 = -6k^2 m-9km^2-k^3\)

Ответ: \(12a^2-16; x^3-27y^3; -x^2 y+2xy^2+y^3; -6k^2 m-9km^2-k^3.\)

Задача 5

Задано несколько выражений, значение которых необходимо вычислить с использованием формул сокращенного умножения и подстановки неизвестных:

\(a^3-b^3-3ab(a-b)\), если \(a = -7; b = -17\)

\(3ab(a+b)+a^3+b^3\), если \(a = -3; b = 13.\)

Решение:

Заменим неизвестные данными числами и воспользуемся правилами сокращенного умножения:

\(a^3-b^3-3ab(a-b) = a^3-b^3-3a^2 b+3ab^2 = a^3-3a^2 b+3ab^2-b^3 = (a-b)^3\)

Путем подстановки получим:

\((-7-(-17) )^3 = 10^3 = 1000\)

Аналогичным способом вычислим второе выражение:

\(3ab(a+b)+a^3+b^3 = 3a^2 b+3ab^2+a^3+b^3 = a^3+3a^2 b+3ab^2+b^3 =(a+b)^3\)

Подставим значения из условия задачи:

\((-3+13)^3 = 10^3 = 1000\)

Ответ: \(1000; 1000.\)

Квадрат разности

Выражение (a — b) 2 — это квадрат разности чисел a и b. Выражение (a — b) 2 представляет собой произведение двух многочленов (a — b)(a — b). Следовательно, из квадрата разности мы можем сделать выводы, что

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:

Многочлен a 2 — 2ab + b 2 называется разложением квадрата разности.

Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.

Пример. Представьте квадрат разности в виде трёхчлена:

Решение: Используя формулу квадрата разности, находим:

(2a 2 — 5ab 2 ) 2 = (2a 2 ) 2 — 2(2a 2 · 5ab 2 ) + (5ab 2 ) 2 .

Теперь преобразуем выражение в многочлен стандартного вида:

(2a 2 ) 2 — 2(2a 2 · 5ab 2 ) + (5ab 2 ) 2 = 4a 4 — 20a 3 b 2 + 25a 2 b 4 .

Примеры задач

Упражнение
Чему равен квадрат суммы (2x + 4y3)2?

Решение
Воспользуемся формулой сокращенного умножения:
(2x + 4y3)2 = (2x)2 + 2 ⋅ 2x ⋅ 4y3 + (4y3)2 = 4×2 + 16xy3 + 16y6

Примечание:
Формулу можно использовать для быстрых расчетов в уме, например:

• 632 = (60 + 3)2 = 602 + 2 ⋅ 60 ⋅ 3 + 32 = 3600 + 360 + 9 = 3969.
• 942 = (90 + 4)2 = 902 + 2 ⋅ 90 ⋅ 4 + 42 = 8100 + 720 + 16 = 8836.

Задание 1

Что делать: вычислить квадрат произведения (55 + 10)2.

Как решить: используем формулу суммы квадратов: (55+10)2=552+2*55*10+102=3025+1100+100=4225.

Задание 2

Что делать: упростить выражение 64*с3 — 8.

Как решаем: используем разность кубов: 64*s3 — 8 = (4*s) 3 — 23 = (4*s — 2) ((4*s) 2 + 4*s * 2 + 22) = (4*с — 2) (16*с2+8*с+4).

Задание 3

Что делать: раскроем скобки (7*у — х)*(7*у+х).

Как мы решаем:

1. Умножьте: (7 * у — х) * (7 * у + х) = 7 * у * 7 * у + 7 * у * х — х * 7 * у — х * х = 49 * у2 + 7 * у * х — 7 * у * х — х2 = 49 * у2 — х2.
2. Воспользуемся приведенной формулой умножения: (7 * у — х) * (7 * у + х) = (7 * у)2 — х2 = 49 * у2 — х2.

Не стоит бояться многочленов, просто выполняйте каждую операцию по порядку. С формулами быстрее и удобнее решать задачи — сохраняйте шпаргалку, запоминайте и радуйте учителей

Умножение разности двух выражений на их сумму

Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

(a − b)(a + b)

В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:

(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2

То есть выражение (a − b)(a + b) равно a2 − b2

(a − b)(a + b) = a2 − b2

Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.

Пример 1. Выполнить умножение (2x − 5)(2x + 5)

В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:

(2x − 5)(2x + 5) = (2x)2 − 52

Вычислим правую часть, получим 4×2 − 25

(2x − 5)(2x + 5) = (2x)2 − 52 = 4×2 − 25

Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4×2 − 25

(2x − 5)(2x + 5) = 4×2 − 10x + 10x − 25 = 4×2 − 25

Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16×2 − 25y2

Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2

В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.

Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.

Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.

Пример 3. Выполнить умножение (7 + 3x)(3x − 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a2 − b2

(7 + 3x)(3x − 7) = (3x)2 − 72 = 9×2 − 49

Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)

(a − b)(a + b) = a2 − b2

(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6

Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)

В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)

Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.

Далее вычисляем выражение в скобках:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25×2 − 9y2)

Теперь умножим −1 на выражение в скобках и получим окончательный результат:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25×2 − 9y2) = −25×2 + 9y2

Тренажер по теме : «Формулы сокращенного умножения»

Тренажер по теме: «Формулы сокращенного умножения» предназначен для тренировки и отработки навыков по данной теме.

Матричная форма записи позволяет организовывать отработку либо заданий одного типа (для этого используются строки), либо целого набора разного вида заданий по теме (для этого используются столбцы).

Тренажер позволяет проводить небольшие самостоятельные работы, а также организовывать индивидуальную коррекционную работу.

Тренажер №1 по теме : «Формулы сокращенного умножения»

№	Задание	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
1	Раскрыть скобки	(a + 2)2	(x + 4)2	(7 + x)2	(2y + 3)2	(5x + 4y)2
2	Раскрыть скобки	( x — 3)2	( a — 5)2	( 8 — x)2	( 3a — 1)2	(8a – 5b)2
3	Представить в виде квадрата суммы	a2+ 4ab +4b2	a2+ 8a +16	25b2+ 10bc +c2	16a2+24ab +9b2	9x2+ 42xy +49y2
4	Представить в виде квадрата разности	9m2— 6mn +n2	m2— 12m + 36	4z2— 20z + 25	36a2— 24ab +4b2	64x2— 48xy +9y2
5	Разложите на множители	25a2 – 9b2	16a2 – 64b2	49x2 – 0,25	81a6 – 25b8	121x2 – 0,16y4
6	Выполните умножение	(2 – 3x)(2 + 3x)	(5x+1)(5x–1)	(7x – 3)(7x + 3)	(4b+5a)(5a–4b)	(2n–3m)(3m+2n)
7	Представьте в виде произведения многочленов	m3+n3	a3+1	8x3+64	27m3+ 8n3	125x3+ 216y3
8	Представьте в виде произведения многочленов	t3 — 64	a3 — 8	27x3 — 125	64m3 – p3	27a3 – 64b3
9	Раскройте скобки	(a + 4)3	(1 +a)3	(x + 3)3	(2a + 1)3	(4x + 2y)3
10	Раскройте скобки	(b — 5)3	(p — 2)3	(4 — b)3	(2x — 3)3	(5a – 3b)3

Тренажер №2 по теме : « Формулы сокращенного умножения»

№	Задание	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
1	Преобразуйте выражение в многочлен	5(4x – 1)2	2a(4 – a)2	(y + 7)23	x2(x + 2)2	x2(x + 2)2
2	Преобразуйте выражение в многочлен	x(x+2)(x—2)	7(2a – 5)(2a +5)	(a3 – 3)(a3 +3)4	(8 – 3x2)(8 + 3x)2x	(3m – 9)(3m + 9)4m2
3	Преобразуйте выражение в многочлен	(2p – 3)(2p + 3) — 11	(4m – 3)(4m + 3) — 2m	4x2— (5x – 2)(5x + 2)	(c2 – 2b)(c2 + 4b)+4c2	25 — (9 – n)(9 + n)
4	Разложите многочлен на множители	25 — (2a +3)2	(4x — 1)2 — 36	49 — (3x -4)2	(3m+5)2 — 64	(7a — 3)2 — 100
5	Разложите многочлен на множители	(2 — x)2 —(3x +5)2	(5 + x)2 —(7 — x)2	(7 +5m)2 —(3m -2)2	(3x — 1)2 —(4 – 2x)2	(a — 2b)2 —(2b + a )2
6	Сократить дробь
7	Сократить дробь
8	Сократить дробь
9	Сократить дробь

Тренажер №3 по теме : « Формулы сокращенного умножения»

№	Задание	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
1	Вычислить, используя формулу квадрата суммы	422	532	612	742	832
2	Вычислить, используя формулу квадрата разности	992	672	482	562	782
3	Вычислить, применив формулу квадрата суммы и квадрата разности:	52 + 2 5 3 + 32	72 — 2 7 3 + 32	42+ 2 4 6 + 62	32— 48 + 82	62+ 108+ 92
4	Вычислить, используя разложение на множители	472 — 372	1262 — 742	532 — 632	472 — 332	792 — 612
5	Вычислить, используя разложение на множители	3,12 – 0,12	2,72 – 0,72	5,82 – 3,82	6,42 – 3,62	8,22 – 1,82
6	Разложите многочлен на множители	3842	56 64	81 99	8179	56 44
7	Разложите многочлен на множители	22 18	37 43	54 46	2713	61 59
8	Вычислить
9	Вычислить