Функция LN в Excel
Это встроенная функция в MS Excel. LN excel относится к категории «Математические функции» в MS Excel. Excel LN используется для вычисления натурального логарифма числа.
Что такое функция натурального логарифма?
Натуральный логарифм числа — это его логарифм по основанию математической константы e , где e — иррациональное и трансцендентное число, примерно равное 2,718281828459. Функция натурального логарифма x обычно записывается как ln x , loge x или иногда, если основание e неявно, просто log x .
Итак, Ln (Number) = LOG (Number, e)
Где e ~ = 2,7128
Ниже представлен график функции LN.
В приведенном выше графике функций LN ось X указывает номер, для которого необходимо вычислить журнал, а ось Y указывает значения журнала. Например, log (1) равен 0, как показано на графике функций LN.
Формула LN в Excel
Формула функции LN Excel выглядит следующим образом:
LN Formula имеет три аргумента, два из которых являются необязательными. Где,
- число = Это обязательный параметр. Он указывает число, для которого должна быть вычислена функция натурального логарифма. Число должно быть положительным действительным числом.
- Если параметр является отрицательным числом, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
- Если параметр равен нулю, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
- Если параметр является нечисловым значением, он возвращает ошибку с #VALUE! указывает на ошибку сгенерированного значения.
Как использовать функцию LN в Excel?
Указанная функция является функцией рабочего листа (WS). Как функцию WS, функцию Excel LN можно ввести как часть формулы в ячейку рабочего листа. Обратитесь к примерам, приведенным ниже, чтобы лучше понять.
Пример # 1 — Дробное число
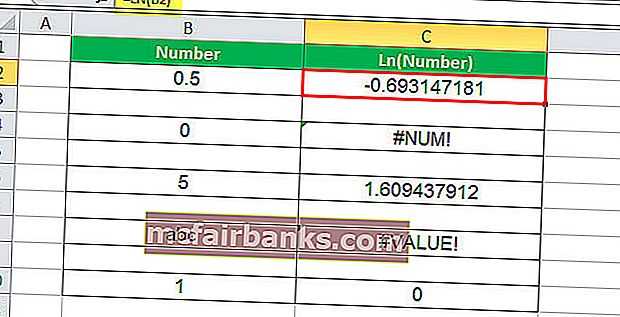
В этом примере с ячейкой C2 связана формула LN. Итак, C2 — это ячейка результата. Первый аргумент LN — это B2, число, для которого необходимо вычислить журнал. Число 0,5, а логарифм 0,5 — -0,693147. Итак, значение результирующей ячейки равно -0,693147.
Пример # 2 — Нулевое число
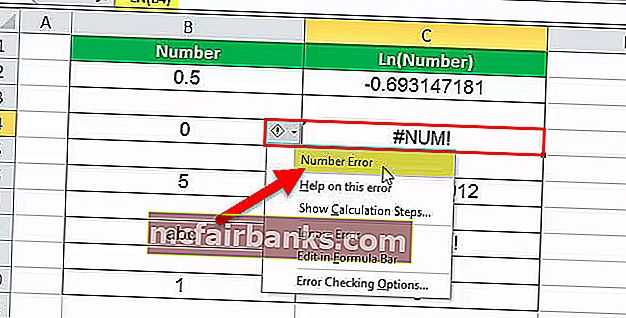
В этом примере с ячейкой C4 связана формула LN. Итак, C4 — это ячейка результата. Первый аргумент LN — это B4, число, для которого необходимо вычислить журнал. Число равно 0, а логарифм 0 не может быть вычислен. Функция LN в Excel не принимает числовое значение как ноль, поэтому в ответ выдается ошибка. Ошибка # ЧИСЛО! что означает, что номер ошибочный.
Пример # 3 — Целое число

В этом примере с ячейкой C6 связана формула LN. Итак, C6 — это ячейка результата. Первый аргумент LN — это B6, число, для которого необходимо вычислить журнал. Число 5, а логарифм 5 — 1,609437912. Итак, значение в результирующей ячейке — 1,609437912.
Пример # 4 — Нечисловое значение
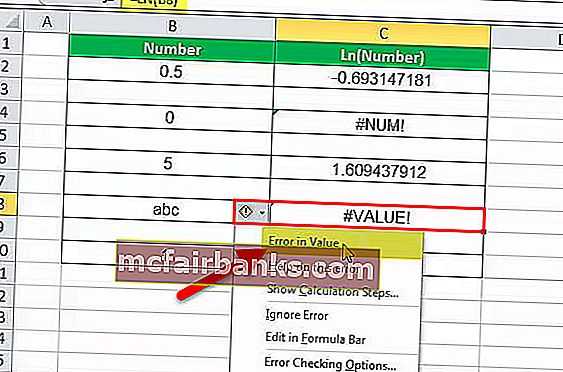
В этом примере с ячейкой C8 связана формула LN. Итак, C8 — это ячейка результата. Первый аргумент LN в Excel — это B8, число, для которого необходимо вычислить журнал. Число — «abc», и журнал нечисловых значений не может быть вычислен. Функция LN в Excel возвращает ошибку, если журнал не может быть рассчитан для такого значения. Ошибка #VALUE! что означает, что значение ошибочно.
Пример # 5 — Отрицательное число
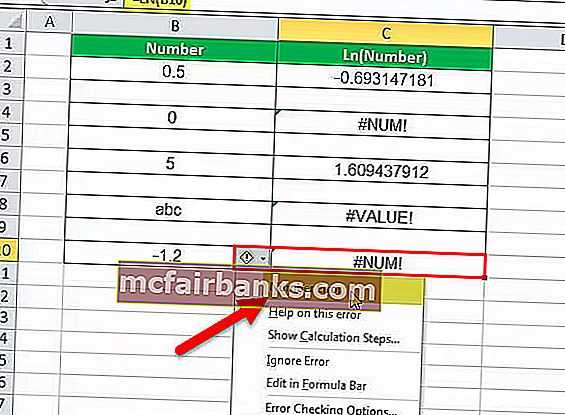
В этом примере с ячейкой C10 связана формула LN. Итак, C10 — это ячейка результата. Первым аргументом LN в Excel является B10, число, для которого необходимо вычислить журнал. Число равно -1,2, и логарифм отрицательного числа не может быть вычислен. Поскольку значение отрицательное, функция LN в Excel возвращает ошибку, указывающую, что значение является ошибочным. Итак, значение в результирующей ячейке — # ЧИСЛО! что означает, что номер ошибочный.
То, что нужно запомнить
- Функция LN в Excel принимает в качестве параметра только положительное действительное число. Делитель не может быть нулевым.
- Если параметр является отрицательным числом, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
- Если параметр равен нулю, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
- Если параметр является нечисловым значением, он возвращает ошибку с #VALUE! указывает на ошибку сгенерированного значения.
Excel VBA для аналогичной цели
VBA имеет отдельную встроенную функцию для вычисления функции натурального логарифма, которая называется LOG. Его можно использовать следующим образом.
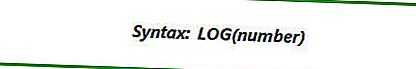
Пример :
Давайте посмотрим на пример, приведенный ниже, для лучшего понимания.
Здесь 5 — это число, для которого должна быть вычислена функция натурального логарифма. Лог (5) по основанию e равен 1.609437912. Итак, переменная logVal содержит значение 1.609437912.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
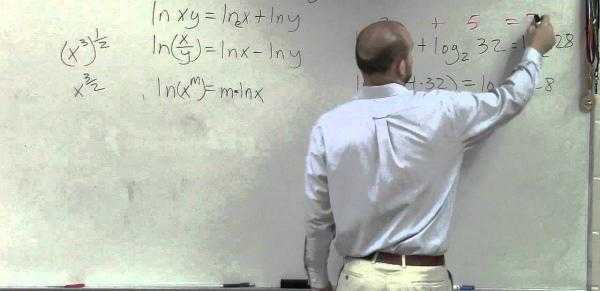
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Вычисление логарифма в Эксель
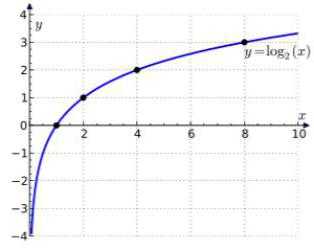
Функция в Excel, позволяющая считать логарифмы из определенного числа по указанному основанию, называется LOG.
Формула функции LOG выглядит следующим образом:
=LOG(число;)
Как мы видим, формула имеет два аргумента:
- “Число” – конкретное число (или адрес ячейки, которая содержит число), из которого требуется вычислить логарифм.
- “Основание” – также выражается числом (либо содержит координаты ячейки с требуемым числом), которое является основанием, по которому вычисляется логарифм. Наличие этого аргумента не является обязательным, и его можно и не указывать. В этом случае автоматически будет присвоено нулевое значение.
Помимо вышеописанной функции, в Эксель есть еще один оператор – LOG10, который вычисляет логарифмы с основанием, равным цифре 10. Другими словами, он умеет работать исключительно с десятичными логарифмами.
Формула функции LOG10 выглядит следующим образом:
=LOG10(число).
В данном случае оператор имеет только один аргумент – “Число”, который, как и в случае с функцией LOG, прописывается в виде числового выражения (либо ссылкой на ячейку с требуемым числом). Это и есть то значение, логарифм которого нужно рассчитать. Второго аргумента под названием “Основание” в этой формуле нет, так как ему присваивается безусловное значение, равное 10.
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма \(log_{a}(b)\) существует только при положительных значениях основания \(a\) и аргумента \(b\). И, кроме этого, на основание накладывается условие, что оно не должно быть равно \(1\).
Почему так? Это следует из определения показательной функции. Показательная функция не может быть равна \(0\) и не может быть меньше \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д
Так как (вспоминайте определение отрицательной степени):
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент под логарифмом в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться, в какую степень \(x\) нужно возвести основание, чтобы получить аргумент. Когда у вас и там, и там степени с одинаковым основанием, посчитать значение логарифма становится проще.
- \(x\) и будет искомым значением логарифма.
Разберем на примерах.
Пример 1Посчитать логарифм от \(9\) по основанию \(3\): \(\quad log_{3}(9)=?\)
- Сначала представим аргумент и основание в виде степеней тройки:
$$ 3=3^1, \qquad 9=3^2;$$
$$log_{3}(9)=log_{3^1}(3^2);$$ - Теперь надо разобраться в какую степень \(x\) нужно возвести \(3^1\), чтобы получить \(3^2\)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2Вычислить логарифм от \(\frac{1}{125}\) по основанию \(5\): \(\quad log_{5}(\frac{1}{125})=?\)
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, \qquad \frac{1}{125}=\frac{1}{5^3}=5^{-3};$$
$$log_{5}(\frac{1}{125})=log_{5^1}(5^{-3});$$ - В какую степень \(x\) надо возвести \(5^1\), чтобы получить \(5^{-3}\):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(\frac{1}{125})=-3.$$
Пример 3Вычислить логарифм от \(4\) по основанию \(64\): \(\quad log_{64}(4)=?\)
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, \qquad 4=2^2;$$
$$log_{64}(4)=log_{2^6}(2^2);$$ - В какую степень \(x\) надо возвести \(2^6\), чтобы получить \(2^{2}\):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=\frac{2}{6}=\frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=\frac{1}{3}.$$
Пример 4Вычислить логарифм от \(1\) по основанию \(8\): \(\quad log_{8}(1)=?\)
- Представим аргумент и основание в виде степени двойки. Напоминаю, что любое число в нулевой степени равно единице:
$$ 8=2^3 \qquad 1=2^0;$$
$$log_{8}(1)=log_{2^3}(2^0);$$ - В какую степень \(x\) надо возвести \(2^3\), чтобы получить \(2^{0}\):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=\frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5Вычислить логарифм от \(15\) по основанию \(5\): \(\quad log_{5}(15)=?\)
Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 \qquad 15= ???;$$
\(15\) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\)? Это довольно просто – нужно разложить \(a\) на простые множители.
\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.
Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) нельзя представить в виде степени какого-нибудь числа.
Депозитный калькулятор со сложным процентом в Excel
Пример 2. Клиент банка внес депозит на сумму 50000 рублей с процентной ставкой 14,5% (сложные проценты). Определить, сколько времени потребуется на удвоение вложенной суммы?
Интересный факт! Для быстрого решения данной задачи можно воспользоваться эмпирическим способом приблизительной оценки сроков (в годах) на удвоение инвестиций, вложенных под сложный процент. Так называемое правило 72 (или 70 или правило 69). Для этого нужно воспользоваться простой формулой – число 72 разделить на процентную ставку: 72/14,5 = 4,9655 лет. Главный недостаток правила «магического» числа 72 заключается в погрешности. Чем выше процентная ставка, тем выше погрешность в правиле 72. Например, при процентной ставки 100% годовых погрешность в годах достигает до 0,72 (а в процентах это аж 28%!).
Для точного расчета сроков удвоения инвестиций будем использовать функцию LOG. За одно и проверим величину погрешности правила 72 при процентной ставке 14,5% годовых.
Вид исходной таблицы:
Для расчета будущей стоимости инвестиции при известной процентной ставке можно использовать следующую формулу: S=A(100%+n%)t, где:
- S – ожидаемая сумма по истечению срока;
- A – размер депозита;
- n – процентная ставка;
- t – срок хранения депозитных средств в банке.
Для данного примера эту формулу можно записать как 100000=50000*(100%+14,5%)t или 2=(100%+14,5%)t. Тогда для нахождения t можно переписать уравнение как t=log(114,5%)2 или t=log1,1452.
Для нахождения значения t запишем следующую формулу сложного процента по депозиту в Excel:
=LOG(B4/B2;1+B3)
Описание аргументов:
- B4/B2 – соотношение ожидаемой и начальной сумм, которое является показателем логарифма;
- 1+B3 – прирост процентов (основание логарифма).
В результате расчетов получим:
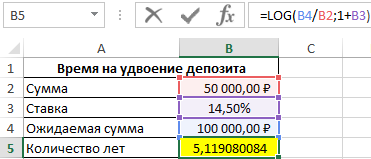
Депозит удвоится спустя немного более чем 5 лет. Для точного определения лет и месяцев воспользуемся формулой:
Функция ОТБР отбрасывает в дробном числе все что после запятой подобно функции ЦЕЛОЕ. Разница между функциями ОТБР и ЦЕЛОЕ заключается лишь в расчетах с отрицательными дробными числами. Кроме того, ОТБР имеет второй аргумент где можно указать количество оставляемых знаков после запятой. Поэтом в данном случаи можно воспользоваться любой из этих двух функций на выбор пользователя.

Получилось 5 лет и 1 месяц и 12 дней. Теперь сравним точные результаты с правилом 72 и определим величину погрешности. Для данного примера формула, следующая:
=72/(B3*100)
Мы должны умножить значение ячейки B3 на 100 так как ее текущее значение 0,145, которое отображается в процентном формате. В результате:

После скопируем формулу из ячейки B6 в ячейку B8, а в ячейке B9:
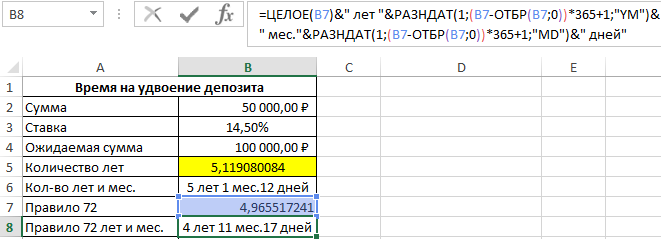
Посчитаем сроки погрешности:
=B5-B7
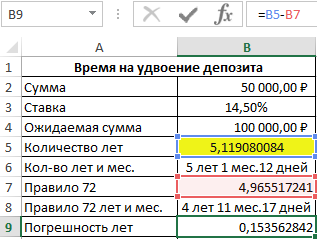
Затем в ячейку B10 снова скопируем формулу из ячейки B6. В результате получим разницу:
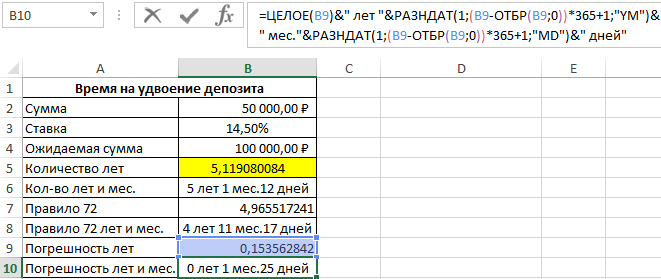
И наконец посчитаем разницу в процентах, чтобы проверить как изменяется размер отклонения и насколько существенно влияет рост процентной ставки на уровень расхождения правила 72 и факта:
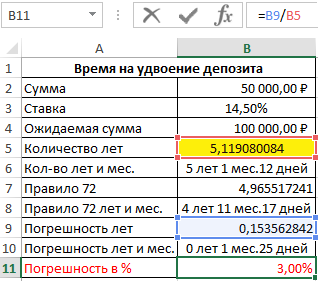
Теперь для наглядности пропорциональной зависимости роста погрешности и роста уровня процентной ставки повысим процентную ставку до 100% годовых:
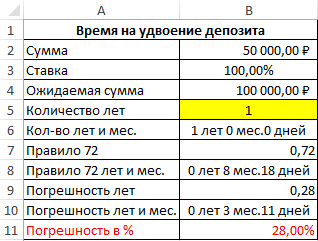
На первый взгляд разница погрешности не существенная по сравнению с 14,5% годовых — всего около 2-ух месяцев и 100% годовых — в пределах 3-х месяцев. Но доля погрешности в сроках окупаемости более чем ¼, а точнее 28%.
Составим простой график для визуального анализа как коррелируется зависимость изменения процентной ставки и процента погрешности правила 72 от факта:
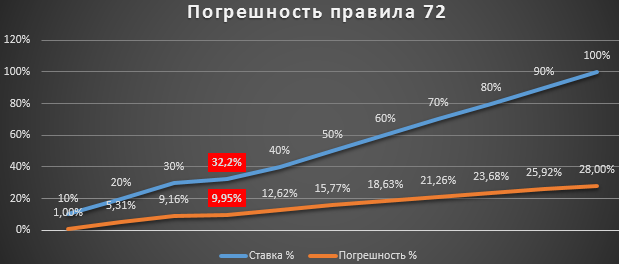
Чем выше процентная ставка, тем хуже работает правило 72. В итоге можно сделать следующий вывод: до 32,2% процентов годовых можно смело пользоваться правилом 72. Тогда погрешность составляет менее 10-ти процентов. Вполне сойдет если не требуются точные, но сложные расчеты по срокам окупаемости инвестиций в 2 раза.
Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.
Например, если при решении уравнения или неравенства требуется преобразовать выражение
loga ( f (x)2 ) ,
то вместо формулы
![]()
следует применять формулу
![]()
поскольку в противном случае можно потерять корни.
По той же причине при преобразовании выражений
loga ( f (x) g (x)) и
следует использовать формулы:
![]()
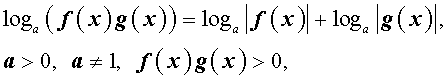
и

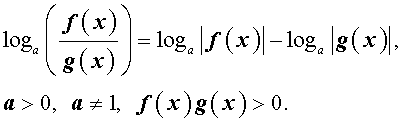
Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».
История.
Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287–212 до н.э.) воспользовался степенями числа 10 8 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную
Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями
М.Штифель в своем сочинении Арифметика целых чисел
(1544) привел таблицу положительных и отрицательных степеней числа 2:
Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке.
По-видимому, правила, аналогичные правилам Штифеля, привели Дж.Нейпера к формальному введению первой системы логарифмов в сочинении Описание удивительной таблицы логарифмов
, опубликованном в 1614. Но мысли Непера были заняты проблемой превращения произведений в суммы еще с тех пор, как более чем за десять лет до выхода своего сочинения Непер получил из Дании известие о том, что в обсерватории Тихо Браге его ассистенты располагают методом, позволяющим превращать произведения в суммы. Метод, о котором говорилось в полученном Непером сообщении, был основан на использовании тригонометрических формул типа
поэтому таблицы Нейпера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 – 10 –7)ґ10 7 , приближенно равное 1/e
.
Независимо от Нейпера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й.Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий
. Это были таблицы антилогарифмов по основанию (1 + 10 –4) ґ10 4 , достаточно хорошему приближению числа e
.
В системе Нейпера логарифм числа 10 7 был принят за нуль, и по мере уменьшения чисел логарифмы возрастали. Когда Г.Бриггс (1561–1631) навестил Непера, оба согласились, что было бы удобнее использовать в качестве основания число 10 и считать логарифм единицы равным нулю. Тогда с увеличением чисел их логарифмы возрастали бы. Таким образом мы получили современную систему десятичных логарифмов, таблицу которых Бриггс опубликовал в своем сочинении Логарифмическая арифметика
(1620). Логарифмы по основанию e
, хотя и не совсем те, которые были введены Нейпером, часто называют нейперовыми. Термины «характеристика» и «мантисса» были предложены Бриггсом.
Первые логарифмы в силу исторических причин использовали приближения к числам 1/e
и e
. Несколько позднее идею натуральных логарифмов стали связывать с изучением площадей под гиперболой xy
= 1 (рис. 1). В 17 в. было показано, что площадь, ограниченная этой кривой, осью x
и ординатами x
= 1 и x
= a
(на рис. 1 эта область покрыта более жирными и редкими точками) возрастает в арифметической прогрессии, когда a
возрастает в геометрической прогрессии. Именно такая зависимость возникает в правилах действий над экспонентами и логарифмами. Это дало основание называть нейперовы логарифмы «гиперболическими логарифмами».
40.500. Логарифмические уравнения
Логарифмом числа $ b $ по основанию $ a(c=log_{a}b) $ называется такой показатель степени $ c $, в которую нужно возвести $ a $, чтобы получить $ b $ (то есть $ a^{c}=b $). При этом задаются ограничения: $ a>0, \; a \neq 1, \; b>0$. Значение $ c $ логарифма может быть любым.
Вычислите:
$ log_{3}27, \; log_{\frac {1}{3}}27 $
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.
$ 3=log_{3}27 $
2. При возведении $ \big(\frac{1}{3} \big)^{-3}=27 $ значит, $ -3=log_{\frac{1}{3}}27 $
Ответ: 3; -3.
Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.
Пусть $ y=log_{2}x $. Подставим вместо $ x $ разные числа и определим соответствующие значения переменной $ y $.
Отметим координаты точек на плоскости и соединим их плавной линией.
Легко заметить, что функция все время возрастает. Такое поведение характерно для всех логарифмических функций с основанием больше единицы.
Пусть теперь $ y=log_{\frac{1}{2}}x $. Составим таблицу значений для этого случая.
Тогда график функции будет выглядеть следующим образом.
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.
Графики всех логарифмических функций проходят через точку с координатами (1;0).
Особыми знаками принято обозначать логарифмы с основанием десять $ log_{10}a=lga $ и логарифмы с натуральным основанием $ e \approx 2.72 \; log_{e} \; a=In \; a $.
Свойства логарифмов
Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.
| Правило | Формула |
| Логарифм 1 по любому основанию равен 0. | $log_{a}1=0$ |
| Логарифм числа по равному ему основанию равен 1. | $log_{a}a=1$ |
| Основное логарифмическое тождество. При разведении основание в степень логарифма получается подлогарифмическое выражение. | $a^{log_{a}b}=b$ |
| Логарифм произведения равен сумме логарифмов. | $log_{a}bc=log_{a}b+log_{a}c$ |
| Логарифм частного равен разности логарифмов. | $log_{a} \frac{b}{c}=log_{a}b-log_{a}c$ |
| Показатель степени можно выносить из подлогарифмического выражения за знак логарифма. | $log_{a}b^{p}=plog_{a}b$ |
| Показатель степени можно выносить из основания логарифма, возводя его в -1 степень. | $log_{a^{a}}b=\frac{1}{q}log_{a}b$ |
| Можно представить логарифмов в виде частного логарифмов с новым основанием. |
$log_{a}b=\frac {log_{c}b}{log_{c}a}$ |
| Если поменять местами подлогарифмическое выражение и основание логарифма, получится логарифм, обратный исходному. | $log_{a}b=\frac {1}{log_{b}a}$ |
Используем рассмотренные свойства для решения некоторых задач.
Пример 2
Вычислите $ log_{5}3125 $
1. Представим $ 3125=5^{5} $.
2. Вынесем степень из—под знака логарифма:
$ log_{5}3125=log_{5}5^{5}=5log_{5}5 $
3. Логарифм числа по равному ему основанию равен 1:
$ 5log_{5}5=5 $
Ответ: 5.
Пример 3
Вычислите $ 5^{2+log_{5}3} $
1. Воспользуемся свойством степеней:
$ 5^{2+log_{5}3}=5^{2} \cdot 5^{log_{5}3} $
2. Используем основное логарифмическое тождество:
$ 5^{2} \cdot 5^{log_{5}3}=25 \cdot 3=75 $
Ответ: 75.
Пример 4
Вычислите $ lg125+lg8 $
1. Воспользуемся формулой для суммы логарифмов:
$ lg125+lg8=lg1000 $
2. Представим 1000 = 103 и вынесем 3 за знак логарифма:
$ lg1000=lg10^{3}=3lg10 $
3. Воспользуемся тем, что $ lg10=1 $.
Ответ: 3.
Пример 5
Вычислить $ log_{36}84-log_{36}14 $.
1. Воспользуемся формулой для частного логарифмов:
$ log_{36}84-log_{36}14=log_{36}6 $
2. Преобразуем основание логарифма 36 = 62 и вынесем, «перевернув», вынесем показатель:
$ log_{36}6=log_{6^{2}}6= \frac {1}{2}log_{6}6 $
3. Воспользуемся тем, что $ log_{6}6=1 $
Ответ: 0,5.
Пример 6
Вычислите $ \frac {lg8+lg18}{2lg2+lg3} $.
1. Применим в числителе формулу для сумы логарифмов:
$ \frac {lg8+lg18}{2lg2+lg3}=\frac {lg144}{2lg2+lg3} $
2. В знаменателе внесем 2 под знак логарифма:
$ 2lg2=lg2^{2}=lg4 $
3. Воспользуемся формулой суммы логарифмов для знаменателя:
$ \frac {lg144}{lg4+lg3}=\frac {lg144}{lg12} $
4. Перейдем от частного к логарифму с основанием 12:
$ \frac {lg144}{lg12}=log_{12}144 $
5. Представим 144 = 122, вынесем степень за знак логарифма и воспользуемся соотношением $ log_{12}12=1 $
$ log_{12}144=log_{12}12^{2}=2log_{12}12=2 $
Ответ: 2.
Кроме выражений с числами, на экзамене могут встретиться выражения, содержащие переменные. В этом случае можно использовать те же формулы и правила.
Пример 7
Вычислите $ log_{125}\frac {a^{2} \cdot a}{a^{3}} $
1. Преобразуем отдельно подлогарифмическое выражение:
$ \frac {a^{2} \cdot a}{a^{3}}=a^{2+1-3}=a^{0}=1 $
2. Логарифм 1 по любому основанию равен 0:
$ log_{125}1=0 $
Ответ: 0.
ПрочитаноОтметь, если полностью прочитал текст






























