Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы . В зависимости от количества сторон многоугольники имеют собственные названия:
- — пентагон;
- — гексагон;
- восемь — октагон;
- двенадцать — додекагон.
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a^2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Шаги
Метод 1 из 3: Вычисление периметра по данной стороне
-
1
Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата. -
2
Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Для определения длины стороны измерьте ее линейкой или посмотрите ее значение в учебнике (задаче). Вот некоторые примеры вычисления периметра:- Если сторона квадрата равна 4, то P = 4 * 4 = 16.
- Если сторона квадрата равна 6, то P = 4 * 6 = 36.
Метод 2 из 3: Вычисление периметра по данной площади
-
1
Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину. Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s2, где s – длина стороны квадрата. -
2
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу «√»). Вы также можете вычислить квадратный корень вручную.- Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
- Если площадь квадрата равна 25, то s = √25 = 5.
-
3
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.- В нашем первом примере: P = 4 * 4,472 = 17,888.
- Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
Метод 3 из 3: Вычисление периметра по данному радиусу окружности, описанной вокруг квадрата
1
Вписанный квадрат – это квадрат, вершины которого лежат на окружности.
2
Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны «a» и «b» и общую гипотенузу «с», равную удвоенному радиусу описанной окружности (2r).
3
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами «а» и «b» и гипотенузой «с»: a2 + b2 = c2. Так как в нашем случае «а» = «b» (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:
a2 + a2 = (2r)2″‘; теперь упростим это уравнение:
2a2 = 4(r)2; теперь разделим обе стороны уравнения на 2:
(a2) = 2(r)2; теперь извлечем квадратный корень из обеих сторон уравнения:
a = √(2r). Таким образом, s = √(2r).
4
Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.
5
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a2) = 202, то есть 2a2 = 400
Теперь разделим обе стороны уравнения на 2 и получим: a2 = 200.
Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142
Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
Вычисление периметра квадрата
Вычислить периметр квадрата несложно и можно сделать в уме. Ввиду того, что все его стороны имеют одинаковую меру, то мы можем определить периметр квадрата, только зная меру одной из сторон. Самое большое определение периметра – это измерение контура двумерной геометрической фигуры.
Итак, исходя из этой концепции, мы можем определить периметр квадрата, сложив каждую сторону этого квадрата. Формула выглядит следующим образом:
P = L + L + L + L или P = L x 4
Где «L» — сторона квадрата.
Пример:
Собственник участка выделил участок площадью 25 м под огороженное место с экраном. Он намерен посадить листья и немного овощей на этом небольшом пространстве. Однако он хочет использовать в этой ручке как можно меньше экрана. Какая плоская геометрическая фигура будет использовать как можно меньший экран, чтобы окружить эту область?
Решение:
В этом случае это было бы возможно только с фигурой четырехугольника.
Начнем с прямоугольника:
Возможные измерения для прямоугольника площадью 25 м будут иметь ширину 4 метра и длину 6,25 метра, откуда мы можем получить периметр:
Р = 4 + 4 + 6,25 + 6,25 = 20,5
Итак, мы знаем, что периметр прямоугольника площадью 25 м эквивалентен 20,5 метрам в длину. В этом случае это будет размер экрана, используемый в данной конфигурации.
Теперь вычислим периметр этой самой площади в 25 м, используя фигуру квадрата.
Единственная возможная мерка для площади 25 м от обычного квадрата – по 5 метров с каждой стороны.
Р = 5 х 4
Р = 20
Итак, мы знаем, что используя угольник, длина периметра забора составит 20 метров. В этом случае владелец участка будет использовать меньше холста с конфигурацией квадрата в своем ограждении.
Эта важная особенность квадрата может остаться незамеченной при проектировании комнаты или любой другой среды. Квадрат всегда будет иметь меньший периметр той же площади по сравнению с другими четырехугольниками.
Как вычислить периметр
Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).
Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.
Теорема Пифагора и её применение
Одна из основных теорем геометрии — Теорема Пифагора — гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора имеет множество применений в различных областях науки и техники. Например, её можно использовать для вычисления расстояния между двумя точками на плоскости, для определения длины сторон треугольника, для расчёта длины пути в лабиринте и многих других задач.
Применение теоремы Пифагора требует умения разбираться в геометрических фигурах и аналитической геометрии. Чтобы успешно применять формулу, необходимо уметь вычислять корни квадратного уравнения и работать с тригонометрическими функциями.
Но несмотря на некоторую сложность, знание теоремы Пифагора и её применения является необходимым для успешного сдачи экзамена по геометрии в ОГЭ по математике. Поэтому рекомендуется хорошо усвоить эту теорему и освоить приёмы её применения.
- Теорема Пифагора является одной из основных теорем геометрии.
- Она позволяет вычислять длину сторон треугольника и расстояние между точками на плоскости.
- Применение теоремы Пифагора требует знания аналитической геометрии и тригонометрии.
- Умение применять теорему Пифагора и её применения необходимо для успешной сдачи экзамена по геометрии в ОГЭ по математике.
Способы вычисления
Для вычисления периметра квадрата применяется несколько видов несложных формул.
По длине стороны
Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:
\(P\;=\;4\times a\,\)
где \(a\) — это сторона фигуры.
По длине диагонали
Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:
\(P\;=\;2d\sqrt2\,\)
что следует из соотношения длин стороны и диагонали \(d=a\sqrt2\)
Зная площадь фигуры, найти ее периметр можно так:
\(P\;=\;4\sqrt S\\\)
По радиусу описанной окружности
Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:
\(P\;=\;4R\sqrt2\,\)
где R — радиус данной окружности.
По радиусу вписанной окружности
Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:
\(P\;=\;8r\,\)
где r — радиус вписанной окружности.
Задача №1
Найти P квадрата, если его ребро a равно 5 см.
Решение:
Так как P = 4a, подставляем сюда известное значение, и получается \(P = 4\times5= 20\ см.\)
Ответ: 20 см.
Задача №2
Узнать P правильного четырехугольника, если его диагональ d равна 6 см.
Решение:
Используем формулу \(P\;=\;2d\sqrt2\) и подставляем известное значение. Получается: \(P = 2 * 6\sqrt2\ = 12\sqrt2\ см.\)
Ответ: \(12\sqrt2\ см.\)
Задача №3
Площадь квадрата равна 16 см². Каков периметр?
Решение:
Мы знаем, что \(P\;=\;4\sqrt S\\\). Значит, подставляя значение в формулу \(P\;=\;4\sqrt S\\\), мы имеем: \(P\;=\;4\sqrt 16\ = 4\times4\ = 16\) см.
Ответ: 16 см.
Задача 4
Задача №4
Известно, что 1/2 диагонали правильного прямоугольника составляет \(9\sqrt2\\ \)см. Вычислить P.
Решение:
1/2 диагонали имеющейся фигуры — это как раз радиус описанной окружности. Подставляем значение в уравнение \(P\;=\;4R\sqrt2\\\). Получается: \(P\;=\;4R\sqrt2\ = 4\times9\sqrt2\times\sqrt2\ = 72\) см.
Ответ: 72 см.
Задача №5
Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.
Решение:
Так как половина стороны данной фигуры — это радиус вписанной в нее окружности. Используем метод нахождения по радиусу вписанной окружности: \(P\;=\;8r\\\). Подставляем известное значение: \(P\;=\;8r\ = 8\times7\ = 56\ см.\)
Круг и его свойства
Определение круга
Круг — это множество всех точек на плоскости, которые находятся на одинаковом расстоянии от ее центра. Расстояние от центра круга до любой его точки называется радиусом круга. Края круга называются окружностью.
Формулы для расчета периметра и площади круга
Периметр круга — это длина его окружности. Ее можно вычислить по формуле:
P = 2πr, где r — радиус круга, π — число Пи (близкое к 3,14).
Площадь круга вычисляется по формуле:
S = πr^2, где r — радиус круга.
Свойства круга
- Любая хорда круга делит его на две равные доли, которые могут быть использованы для нахождения различных свойств круга.
- Угол, образованный двумя радиусами круга, равен 90 градусам.
- Если к точке пересечения двух хорд круга провести перпендикуляры, то точка пересечения будет являться центром окружности, описанной вокруг круга.
- Круг может быть вписан в любой четырехугольник таким образом, что он будет касаться всех его сторон.
Пример задачи
Дан круг с радиусом 5 см. Найдите его площадь и периметр.
Решение:
- Периметр круга: P = 2πr = 2*3,14*5 = 31,4 см
- Площадь круга: S = πr^2 = 3,14*5*5 = 78,5 см^2
Треугольник и его свойства
Соотношение между углами треугольника
Треугольник — это многоугольник соответствующий которому имеет три вершины и три стороны. Одно из важных свойств треугольника заключается в том, что сумма всех его углов равна 180 градусов. Также стоит отметить, что наибольший угол треугольника всегда находится напротив наибольшей стороны, наименьший угол — напротив наименьшей его стороны.
Неравенство в треугольнике: любая сторона треугольника меньше суммы двух других сторон и больше разности между ними.
Типы треугольников
Существует несколько типов треугольников, различающихся по длинам сторон и величине углов. Так, треугольник может быть равносторонним, равнобедренным, прямоугольным и разносторонним.
- Равносторонний треугольник — все стороны и углы равны.
- Равнобедренный треугольник — имеет две равные стороны, а углы напротив определенных сторон также равны.
- Прямоугольный треугольник — характеризуется наличием прямого угла. Сторона противолежащая прямому углу называется гипотенузой.
- Разносторонний треугольник — все три стороны и углы различны.
Формулы для вычисления площади и периметра треугольника
Для расчета периметра треугольника надо сложить длины всех его сторон.
Площадь треугольника можно вычислить, используя следующие формулы:
- Если известна длина основания (стороны) и высоты (отрезка, проведенного к середине этой стороны из противоположной вершины), то площадь равна половине произведения основания на высоту. S = (a*h)/2.
- Формула Герона: для нахождения площади треугольника по трем сторонам можно воспользоваться формулой Герона, которая выглядит следующим образом: S = √(p*(p-a)*(p-b)*(p-c)), где p=(a+b+c)/2 — полупериметр треугольника, a, b, c — длины его сторон.
Нахождение периметра квадрата
Определение
Квадрат – это такой четырехугольник, который обладает свойствами прямоугольника, параллелограмма, а также ромба:
- Все стороны равны.
- Все углы прямые, то есть по 90°.
- Диагонали равны, а угол их пересечения прямой.
- Диагонали при пересечении делать эти углы пополам.
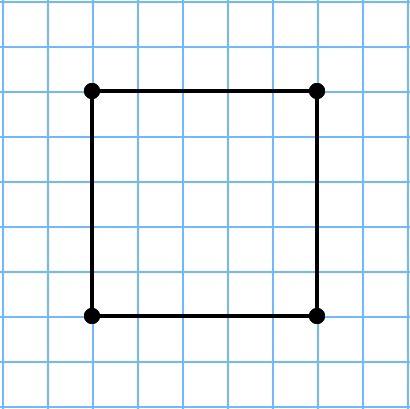Квадрат
Зная свойства квадрата, можно понять, что его периметр находится путем сложения всех 4 сторон или же умножения его одной стороны на 4. Из этого выведем формулу где a – сторона квадрата:
\
\
Пример 1
Найдите периметр квадрата, сторона которого равна 6 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + a + a
6 + 6 + 6 + 6 = 24 (см)
Ответ: периметр этого квадрата равен 24 см.
Пример 2
Найдите периметр квадрата, сторона которого равна 10 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 4a
4 × 10 = 40 (см)
Ответ: периметр равен 40 см.
Применение периметра квадрата в повседневной жизни
Знание периметра квадрата может быть полезным во многих аспектах нашей повседневной жизни. Вот несколько примеров, где мы можем использовать понятие периметра:
- Расстановка мебели в комнате: Если у вас есть квадратная комната, вы можете использовать периметр квадрата для расстановки мебели так, чтобы она наилучшим образом использовала пространство. Вы можете измерить периметр комнаты, чтобы понять, сколько мебели вам нужно, и где она будет находиться.
- Изготовление рамок и фреймов: Периметр квадрата может быть использован для определения длины сторон рамки или фрейма, который нужно изготовить. Зная периметр квадрата, можно легко рассчитать длину каждой стороны и изготовить точно подходящую рамку или фрейм для фотографий или картин.
- Расчет габаритов для строительства: Периметр квадрата имеет прямое отношение к габаритам, используемым в строительстве. Зная периметр квадрата здания или участка земли, можно легче подсчитать, сколько материалов нужно для строительства ограждений, заборов или дорожек.
- Планирование посадки: В садоводстве и ландшафтном дизайне, периметр квадрата может использоваться для планирования расстановки растений и создания кварталов или цветочных клумб. Зная периметр участка, можно точно рассчитать расстояния между растениями и создать гармоничный дизайн.
- Определение площади: Площадь квадрата может быть вычислена с помощью периметра, зная, что все стороны квадрата равны. Это может быть полезно при покупке коврового покрытия или покрытия пола, чтобы определить необходимое количество материала.
Как видите, периметр квадрата имеет множество применений в повседневной жизни. Понимание этой концепции может помочь вам в различных ситуациях, когда требуется измерение или оценка размеров. Будь то дизайн интерьера, строительство или садоводство, недооценивайте роль периметра квадрата в нашей повседневной жизни.
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни . И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей . Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Наверняка каждый из нас учил в школе такую важную составляющую геометрии, как периметр. Нахождение периметра просто необходимо для решения множества задач. О том, как найти периметр, расскажет наша статья.
Стоит помнить, что периметр любой фигуры это почти всегда сумма ее сторон. Давайте рассмотрим несколько разных геометрических фигур.
В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.
Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).
Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.
Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.
C)
.
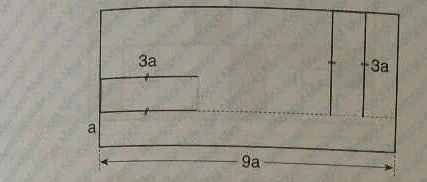
Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника
В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a
.
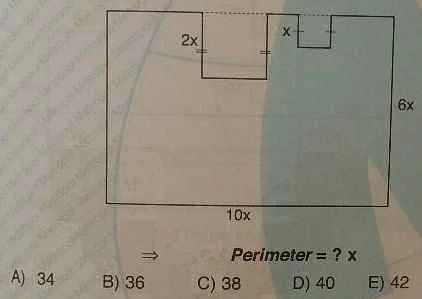
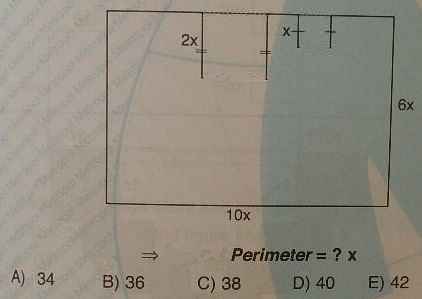
C)
.
После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.
Итого, P=32x+2∙2x+2∙x=38x
.
?)
.
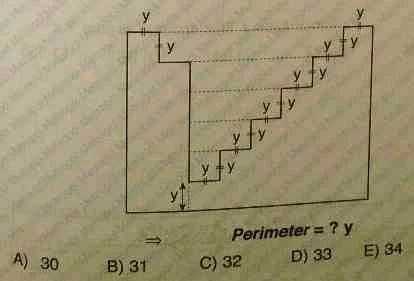
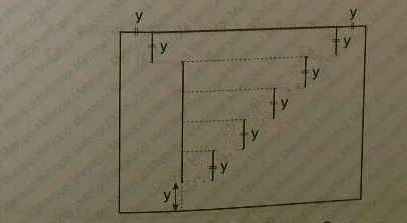
Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y
.
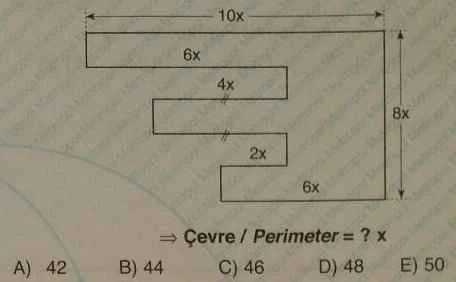
D)
.
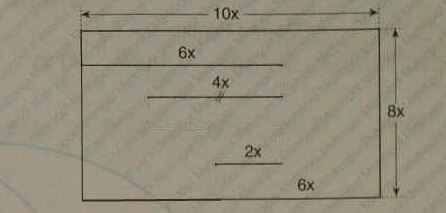
Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.
Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x
.
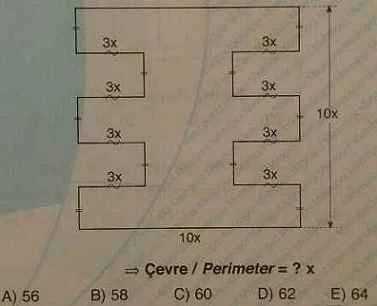
E)
.
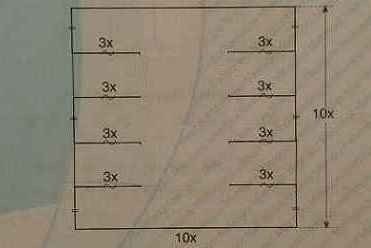
Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x
.
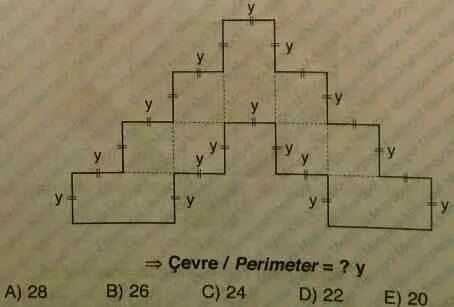
B)
.
Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y
.
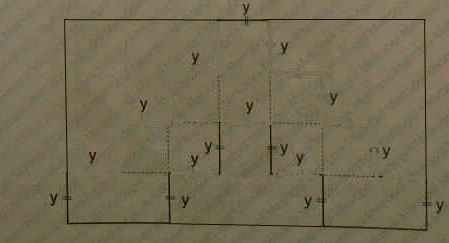
D)
.
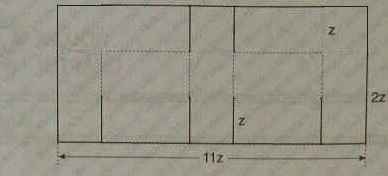
Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.
Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z
.
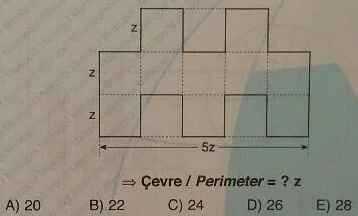
B)
.
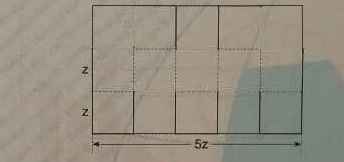
Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:
P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z
.
Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.
