Онлайн калькуляторы расчёта длины, площади, радиуса круга. формулы расчёта

Вопрос-ответ:

Какой квадрат возможно вписать в окружность?

В окружность можно вписать квадрат любого размера, однако максимальный размер квадрата в окружности равен диаметру окружности. Если диаметр окружности равен d, то сторона квадрата будет равна d/√2.

Как найти площадь квадрата, вписанного в окружность?

По теореме Пифагора можно найти длину стороны квадрата, если известен диаметр окружности. Сторона квадрата равна d/√2, где d — диаметр окружности. Площадь квадрата равна длине стороны в квадрате: S = (d/√2)2.

Можно ли найти площадь квадрата, вписанного в окружность, если известна его диагональ?

Да, можно. Если известна длина диагонали квадрата, то можно найти его площадь, используя формулу S = (d2/2), где d — длина диагонали. Для квадрата, вписанного в окружность, диагональ равна диаметру окружности.

Как проверить, что квадрат правильно вписан в окружность?

Если квадрат правильно вписан в окружность, то его стороны будут пересекать окружность в точках, являющихся серединами дуг окружности. Также можно проверить, что диагональ квадрата равна диаметру окружности.

Можно ли вписать в окружность прямоугольник?

Да, в окружность можно вписать прямоугольник, но это возможно только в том случае, если прямоугольник является квадратом или ромбом. Для этого нужно взять перпендикуляр к диагонали прямоугольника на середине диаметра окружности, а затем построить прямые, параллельные этому перпендикуляру, проходящие через противоположные вершины прямоугольника.

Как найти радиус вписанной окружности в квадрате

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в квадрат. Также разберем примеры решения задач для закрепления теоретического материала.

Формулы вычисления радиуса вписанной окружности

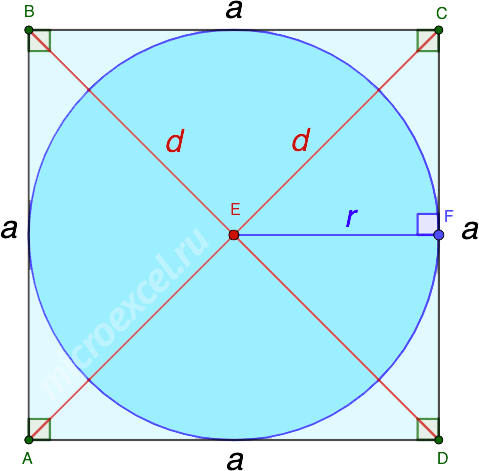
Радиус r вписанной в квадрат окружности равняется половине длины его стороны a.

Через диагональ квадрата

Радиус r вписанной в квадрат окружности равняется длине его диагонали d, деленной на произведение числа 2 и квадратного корня из двух.

Примеры задач

Задание 1

Найдите радиус вписанной в квадрат окружности, если известно, что длина его стороны равняется 7 см.

Воспользуемся первой формулой, подставив в него известное значение:

Задание 2

Известно, что радиус вписанной в квадрат окружности составляет 12 см. Найдите длину его диагонали.

Формулу для нахождения диагонали можно вывести из формулы для расчета радиуса круга:

Окружность вписанная в квадрат

Чтобы формула нахождения радиуса вписанной окружности в квадрат r вычислялась правильно, необходимо сначала вспомнить, какими свойствами обладает эта фигура.
На площади:

все углы прямые, то есть равны 90°;
все стороны, как углы, равны;
диагонали равны, точка пересечения строго делится пополам и пересекается под углом 90°.

При этом окружность, вписанная в выпуклый многоугольник, обязательно касается всех сторон. Обозначим квадрат ABCD, пересечение диагоналей O. Как видно из рисунка 1, пересечение прямых AC и BD дает равнобедренный треугольник AOB, где стороны AO=OB, углы OAB=ABO=45 °, а угол АОВ=90°. Тогда радиус вписанной окружности в квадрат будет не чем иным, как высотой ОЕ получившегося равнобедренного треугольника АОВ.

Если принять, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть так:

Пояснение: в равнобедренном треугольнике AOB высота OE или радиус r делит основание AB пополам (свойства), образуя прямоугольный треугольник с прямым углом OEB. В малом треугольнике EBO основание OB образует углы 45° со сторонами OE и EB. Значит треугольник EBO тоже равнобедренный. Стороны ОЕ и ЕВ равны.

Для наглядности приведем численный пример нахождения значения радиуса вписанной окружности в квадрат со стороной, равной 13 см. В этом случае значение вписанного радиуса будет:
Решение обратной задачи также несложно. Предположим, что известен радиус вписанной окружности — 9 см, тогда, разобрав пример нахождения значения радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим неизвестное значение из этого уравнения:
.

Как найти радиус вписанной в квадрат окружности

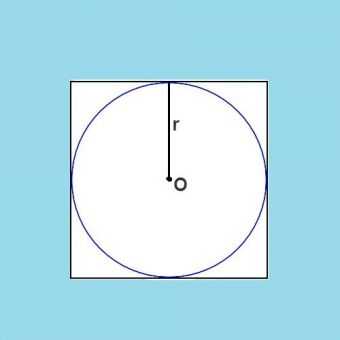
Можно рассмотреть простейший пример: периметр квадрата составляет 28 см, требуется найти радиус вписанной в этот квадрат окружности. Сначала стоит знать, что периметр квадрата равен сумме всех его сторон. Стороны равны между собой, а их всего 4.

Значит длина стороны квадрата вычисляется так: 28 см/4=7 см.Теперь надо воспользоваться формулой, выведенной выше:r=7/2=3,5 см.Ответ: радиус окружности, вписанной в квадрат, составляет 3.5 см.

Как найти радиус круга, если известна его площадь
Как вычислить диагональ квадрата
Как вычислить сторону квадрата

Как определить радиус окружности
Как построить вписанную окружность
Как найти радиус
Как находить площадь квадрата
Как найти длину стороны квадрата
Как определить радиус круга
Как найти площадь круга
Как найти площадь вписанной окружности
Как вычислить радиус
Как вписать в выпуклый четырехугольник окружность
Как находить периметр ромба
Как найти периметр квадрата, если известна его площадь
Как найти окружность, зная только радиус
Как найти периметр шестиугольника
Как найти периметр, зная площадь квадрата
Как найти площадь шестиугольника
Как посчитать радиус
Как находить площадь круга
Как найти радиус описанной около треугольника окружности
Как найти радиус вписанной в прямоугольный треугольник окружности
Как найти сторону правильного треугольника
Как найти радиус окружности, вписанной в ромб
Как найти сторону правильного шестиугольника

Список литературы

Внимание! При использовании материалов из списка литературы необходимо указывать источник

Научные статьи

А.А. Болотов, А.В. Кузнецов. «О вписанной окружности в квадрат». Математические заметки, 2010, том 88, выпуск 2, с. 163-168.
И.И. Горбунов, В.А. Красносельский. «О вписанной окружности в квадрат». Математические заметки, 2005, том 78, выпуск 1, с. 3-10.
А.В. Погорелов. «О вписанной окружности в квадрат». Математические заметки, 1965, том 1, выпуск 2, с. 211-214.

Учебники и справочники

А.Д. Александров, В.П. Маслов, В.М. Тихомиров. «Математическая энциклопедия». Москва, Советская энциклопедия, 1977.
В.И. Арнольд. «Математические методы классической механики». Москва, Наука, 1989.
В.А. Рохлин. «Основы топологии». Москва, Наука, 1977.

Интернет-ресурсы

Название	Адрес
Wolfram MathWorld	https://mathworld.wolfram.com/Incircle.html
Brilliant	https://brilliant.org/wiki/incircle/
Geogebra	https://www.geogebra.org/m/xyjzjzjv

Использование различных источников позволяет получить более полное представление о теме и углубить свои знания в математике.

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Диаметр вписанной окружности квадрата Решение

ШАГ 0: Сводка предварительного расчета

Используемая формула

Диаметр вписанной окружности квадрата = Длина края квадрата/1D_i = l_e/1В этой формуле используются 2 Переменные

Используемые переменные

Диаметр вписанной окружности квадрата — (Измеряется в метр) — Диаметр вписанной окружности квадрата — это диаметр вписанной окружности квадрата или круга, содержащегося в квадрате, при этом все ребра квадрата касаются круга.Длина края квадрата — (Измеряется в метр) — Длина края квадрата — это длина любого из четырех краев квадрата.

ШАГ 1. Преобразование входов в базовый блок

Длина края квадрата: 10 метр —> 10 метр Конверсия не требуется

ШАГ 2: Оцените формулу

Подстановка входных значений в формулу

D_i = l_e/1 —> 10/1

Оценка … …

D_i = 10

ШАГ 3: Преобразуйте результат в единицу вывода

10 метр —> Конверсия не требуется

ОКОНЧАТЕЛЬНЫЙ ОТВЕТ

10 метр <— Диаметр вписанной окружности квадрата

(Расчет завершен через 00.003 секунд)

Квадрат — определение и свойства

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

Все углы квадрата — прямые, все стороны квадрата — равны.
Диагонали квадрата равны и пересекаются под прямым углом.

Периметр квадрата P в 4 раза больше его стороны и равен:

Площадь квадрата равна квадрату его стороны: .

Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть .

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

Тогда , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

Все стороны равны и среди внутренних углов есть прямой угол.
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна .

Мы знаем, что . Тогда .

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

Тогда по формуле площади квадрата:

Второй способ решения:

Воспользуемся формулой для площади ромба:

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной .

Радиус описанной окружности равен половине диагонали квадрата, поэтому

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Диаметр окружности равен стороне квадрата: .

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Найдем сторону квадрата:

Периметр квадрата со стороной 3 равен:

Задача 8. Найдите площадь квадрата, в который вписан круг площадью .

Площадь круга откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .