Деление десятичных дробей, правила, примеры, решения

Алгоритм сложения (вычитания) десятичных дробей

Сложение и вычитание десятичных дробей можно выполнить, следуя данному алгоритму:

Уравняйте количество знаков после запятой в дробях, добавив недостающие нули.
Запишите дроби одну под другой, выровняв запятые.
Выполните сложение или вычитание без учета запятых.
Поставьте запятую в ответе под запятой.

Пример:

Дано: $0,25 + 0,8$

Шаг 1: Уравняйте количество знаков после запятой: $0,25 + 0,80$

Шаг 2: Запишите дроби одну под другой:

\begin{align*}

&0,25 \\

+ &0,80 \\

\hline

\end{align*}

Шаг 3: Выполните сложение без учета запятых: $0,25 + 0,80 = 1,05$

Шаг 4: Поставьте запятую в ответе под запятой: $1,05$

Таким образом, результат сложения $0,25 + 0,8$ равен $1,05$.

Ведение математических записей

Ключевое преимущество рассматриваемых дробей состоит в том, что запись получается максимально понятной и аккуратной. В математике активно используется десятичная запись, где целую часть можно легко отделить от дробной при помощи обычной запятой. При этом сам разделитель называется десятичной точкой. К примеру: значение 0,5 все читают как ноль целых, 5 десятых.

В качестве точки принято использовать обычную запятую. Чтобы правильно записать произвольную дробь в необходимой форме, нужно учесть три базовых правила:

Числитель всегда вписывают отдельно.
Необходимо посчитать, сколько нулей содержится в знаменателе, поскольку это количество знаков определяет перенос точки.
Если после совершенных действий остались нули, то их лучше зачеркнуть.

Часто можно наблюдать ситуацию, что на втором шаге у числителя не хватает цифр для полноценного сдвига всей конструкции. В таком случае все недостающие позиции обязательно заполняются нулями. Этот алгоритм может оказаться довольно сложным, но на практике всё просто. Для изучения всех тонкостей следует рассмотреть примеры задач, в которых необходимо указать правильную арифметическую форму для следующих примеров:

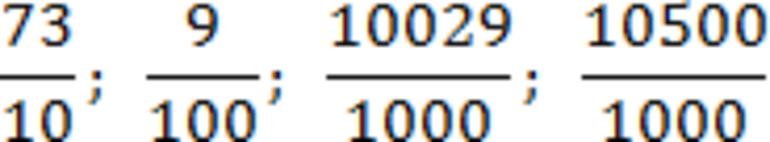
В первом случае числителем дроби является 73. Имеющуюся точку следует сдвинуть всего на один символ, благодаря чему получим 7,3. Во втором примере числителем является 9. Сдвигать запятую нужно уже на целых два знака, так как в знаменателе стоит 100. В итоге получим 0,09. В последнем случае имеем дело с большим числителем — 10500. Запятую сдвигаем уже на три знака и получаем 10,500. Но после проделанных манипуляций в конце числа образовались ненужные нули. Если их зачеркнуть, можно получить более приглядный результат — 10,5.

Следует обратить внимание на числа 120,7 и 11,036. Если чётко следовать математическим правилам, то ненужные нули справа следует зачеркнуть

Но такие действия просто недопустимы по отношению к нулям, которые расположены внутри числа. Именно поэтому правильное решение задач будет иметь следующий вид: 120,7, 11,036, а не 12,7 и 11,36.

Округление натуральных чисел 5 класс

Практически каждый день мы используем округление. Например, если от школы до дома расстояние — 602 метра, мы говорим, округляя значение, что это расстояние — 600 метров. Т.е., число 602 мы приблизили к числу 600, что воспринимается легче. Еще один пример — батон хлеба весит 397 грамм, округлив можно сказать, что батон весит 400 грамм.

В результате, при округлении, мы получаем «приближенное» число. Обозначается округление знаком ≈, который читается — приближенно равно (приблизительно).

Пример: 604≈600; 597≈600. Читается — шестьсот четыре приближенно равно шестистам и пятьсот девяносто семь приближенно равно шестистам.

Посмотрим еще примеры:

В примере мы видим округление до тысяч

Обратите внимание, что округление происходит в одном случае в большую сторону, а в другом в меньшую. Все числа после округления заменены на нули

Дробь — знак деления

Даже на калькуляторе обычно деление отображается как знак дроби. А еще можно иногда встретить вот такое написание дробей: $\textcolor{coral}{½}, \space \textcolor{green}{3/4}$.

пример

Мама купила $12$ мандаринов: себе, папе и двоим детям. По сколько мандаринов достанется каждому, если разделить их поровну?

$$\frac{12}{4}=3$$

деление нацело

Иногда дробь можно «поделить до конца» и получить целое число. В таких случаях говорят, что деление выполняется нацело.

Выглядит это, как будто мы записали пример, а решать его поленились:

$$4:5=\frac{4}{5}$$

{"questions":,"items":}},"step":1,"hints":}]}

Дроби — коротко о главном

Определения:

Делимое $\displaystyle a$ – числитель дроби, а делитель $\displaystyle b$ – знаменатель дроби.

Например: $\displaystyle\frac{2}{5}$, $\displaystyle\frac{1}{7}$ и так далее.

Например: $\displaystyle\frac{9}{5}$, $\displaystyle\frac{13}{2}$ и так далее.

Например: $\displaystyle2\frac{2}{5}$$ \displaystyle \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}$.

Например: $\displaystyle\frac{9}{100}$ в виде десятичной дроби записывается как $\displaystyle0,09$,

$\displaystyle\frac{225}{1000}$ записывается как $\displaystyle0,225$.

Основное свойство дроби:

Например: $\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}$.

Действия с дробями:

Сложение/вычитание дробей

две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: $\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$
две обыкновенные дроби с разными знаменателями:
- приводим дроби к наименьшему общему знаменателю;
- складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
- сокращаем полученную дробь
две смешанные дроби с разными знаменателями:
- приводим дробные части этих чисел к наименьшему общему знаменателю;
- по-отдельности складываем/вычитаем целые части и дробные части;
- если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
- сокращаем полученную дробь.

Умножение дробей

умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
умножение двух обыкновенных дробей:
- перемножаем числители и знаменатели дробей;
- сокращаем полученную дробь
умножение двух смешанных чисел:
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем полученную дробь;
- если получилась неправильная дробь преобразовываем ее в смешанную.

Деление дробей

деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
деление натурального числа на дробь: число умножаем на дробь обратную данной
деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
деление двух смешанных чисел:
- преобразовываем смешанные дроби в неправильные;
- умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.

Сокращение дроби

Например: $\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}$.

Приведение дробей к наименьшему общему знаменателю

найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.

Например: $\displaystyle\frac{1}{3}$ и $\displaystyle\frac{3}{4}$. Наименьший общий знаменатель — $\displaystyle12$.

Дополнительный множитель первой дроби — $\displaystyle12:3=4$, дополнительный множитель второй дроби — $\displaystyle12:4=3$.

Следовательно: для первой дроби: $\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}$, для второй дроби: $\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}$.

Преобразования неправильной дроби в смешанную дробь

поделите числитель дроби на ее знаменатель;
остаток от деления запишите в числитель, знаменатель оставьте прежним;
результат от деления запишите в качестве целой части.

Например: $\displaystyle\frac{17}{4}$ = $\displaystyle4\frac{1}{4}$.

Сравнение дробей:

две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше

Умножение десятичных дробей на 10, 100, 1000

Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.

Например, умножим 2,88 на 10

Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:

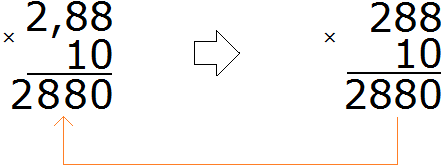
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.

Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:

Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8

2,88 × 10 = 28,8

Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.

Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.

2,88 × 10 = 28,8

Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288

2,88 × 100 = 288

Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.

2,88 × 1000 = 2880

Применение целых чисел

При делении крайне важно учитывать то, в каком виде должен быть представлен итоговый результат. Он может быть дробным или десятичным

Для более тщательного изучения этой темы нужно рассмотреть все варианты. Чтобы после выполнения математических действий можно было получить искомую дробь, нужно конкретный делитель и делимое число представить в наиболее подходящем виде. В качестве примера можно разделить 18 на 1,9. Число 18 стоит представить в виде 18/1. Это значит, что 1,9 нужно перевести в 19/10.

Для правильного выполнения арифметических действий дробь переворачивается, а результат перемножается. Пример: 18/1: 19/10 = 18/1: 10/19 = 180/19. Если нужно, то полученный результат можно быстро привести в обычный десятичный вид. Чтобы выполнить деление в столбик, следует учесть тот факт, что когда остаётся неделимый остаток, то ставится обычная запятая, а затем дописывается столько нулей, сколько нужно для конкретного случая.

Если перед учащимся была поставлена задача поделить целое число на десятичное, но результат должен быть представлен в виде неправильной или правильной дроби, тогда нужно умножить делитель и делимое на 10. В итоге должно получиться целое число. В математике запятая обязательно переносится на несколько знаков. Пример: 72:3,6 = 720:36 = 20. Если по условиям было 0,36, тогда следует умножить на 100.

Чтобы избежать ошибок, нужно помнить, что для деления действует основное правило использования знаков умножения. Если работать сразу с двумя отрицательными числами, то в итоге можно получить необходимый положительный результат. Но если разделить положительный пример на отрицательный, тогда будет получено значение со знаком минус. Не стоит пугаться больших результатов, поскольку такая ситуация вполне естественна. Если целое число будет поделено на дробное, то результат будет больше делимого. Стоит учесть, что под правильной дробью принято понимать пример, который меньше единицы.

Основные понятия

Арифметика — одна из основных разделов математики, которая изучает свойства чисел и основные операции над ними, такие как сложение, вычитание, умножение и деление.

Число — абстрактное понятие, представляющее собой некий количественный показатель. Числа можно представить в различных формах, например, в виде целых чисел, десятичных дробей или обыкновенных дробей.

Представить число в виде дроби — значит выразить число в форме отношения двух целых чисел, где числитель это целое число, а знаменатель — натуральное число. Это позволяет исследовать и работать с дробными числами более удобным образом.

Наоборот, представить дробь в виде числа — это процесс, обратный представлению числа в виде дроби. Это может включать округление десятичных дробей или перевод обыкновенной дроби в десятичную форму.

Разложение числа — это процесс представления числа в виде суммы или произведения других чисел. Например, разложение числа 12 на множители может быть выражено как 2 * 2 * 3.

Алгебра — раздел математики, изучающий структуры и операции над ними. Алгебра позволяет решать уравнения, работать с переменными и изучать различные алгебраические объекты, такие как многочлены и матрицы.

Числитель и знаменатель

В математике арифметика и алгебра тесно связаны с понятием дроби. Дробь представляет собой часть целого числа, состоящую из числителя и знаменателя. Числитель — это число, которое находится вверху дроби, а знаменатель — это число, которое находится внизу дроби.

Чтобы представить число в виде дроби, необходимо разложить его на числитель и знаменатель. Числитель выражает количество частей целого, которое мы хотим представить в виде дроби, а знаменатель определяет количество частей, на которые мы делим целое число.

Например, чтобы представить число 3/4 в виде дроби, мы разделяем целое число на 4 равные части, и выбираем 3 из них в качестве числителя. Таким образом, число 3/4 означает, что мы выбираем 3 равные части из 4 возможных.

Наоборот, чтобы представить дробь в виде числа, необходимо выполнить операцию деления числителя на знаменатель. Например, чтобы представить дробь 2/5 в виде числа, мы делим числитель 2 на знаменатель 5. Результатом будет десятичная дробь 0.4. Таким образом, дробь 2/5 соответствует числу 0.4.

Используя арифметические операции, разложение числа на числитель и знаменатель позволяет нам работать с дробями и представлять их в разных формах, будь то в виде десятичной дроби или обыкновенной дроби.

Операции над дробями

С дробями можно совершать различные арифметические операции.

Сложение

Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.

Далее — выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.

В конце, если возможно, сократить полученную дробь.

Например:

Вычитание

Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.

Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.

Например:

Умножение

Для этого умножаются числители и записывается результат, как числитель дроби.

Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.

Например:

Деление

Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.

Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.

Например:

Сокращение

Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.

В итоге получается равную дробь, имеющая меньший знаменатель и числитель.

Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.

Значительно упростит сокращение раскладывание знаменателя и числителя на множители.

Например:

Вопросы и ответы

А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них

Какие дроби называются простыми?

Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.

Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название — десятичные.

Правильные дроби те, у которых модуль знаменателя больше модуля числителя.

Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.

Нельзя делить на 0.

Если делить на 1 — будет такое же число.

Если делить 0 на любое число, получится 0.

Когда она больше 0.

Когда перед положительной дробью ставится знак «–».

Что такое степени с дробями?

Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.

При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.

Как пользоваться калькулятором дробей?

Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.

Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».

Действия с десятичными дробями

Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.

Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене. Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению

Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.

Как складывать десятичные дроби

При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.

Разберемся на примере:

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.

Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Если при сложении в сумме мы получаем больше $ 10$, то одна единица прибавляется к сумме при сложении цифр следующего разряда.

Решим наш пример, учтя все правила:

Разобрался? Посчитай в столбик самостоятельно:

$ 0,0125+0,141$
$ 2,4225+0,34$
$ 122,4355+1,34$
$ 2,435+12,3$

Сравним ответы:

$ 0,0125+0,141=0,1535$
$ 2,4225+0,34=2,7625$
$ 122,4355+1,34=123,7755$
$ 2,435+12,3=14,735$

Представление дроби в виде числа

Алгебра и арифметика предоставляют нам инструменты для представления дроби в виде числа и наоборот. Дробь — это математический объект, который представляет отношение двух чисел. В числителе записывается число, которое представляет часть от целого, а в знаменателе записывается число, которое определяет, на сколько частей целое было разделено.

Представление дроби в виде числа может быть достигнуто путем выполнения операции деления числителя на знаменатель. В результате этой операции получается число, которое представляет отношение между числителем и знаменателем. Например, дробь 3/4 можно представить в виде числа 0.75.

Однако, не все дроби можно представить в виде конечной десятичной дроби. Некоторые дроби имеют периодическое разложение в десятичную дробь, что значит, что после запятой будет повторяться один или несколько цифр или групп цифр.

Для представления дроби в виде числа можно использовать и другие методы, такие как разложение на непрерывную десятичную дробь или представление в виде смешанной числовой дроби, где число разделено на целую часть и часть после запятой.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

Это выражение можно прочитать по-разному:

В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.

Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

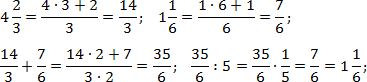
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

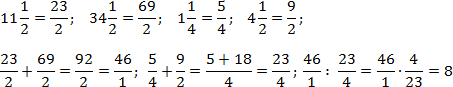
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

Умножение и деление дробей
Тест к уроку «Сложные выражения с дробями» (легкий)
Тест к уроку «Округление с избытком и недостатком» (1 вариант)
Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
Формула простого процента: как найти исходное значение
Сложная задача B14 на смеси и сплавы

Алгоритм сложения (вычитания) десятичных дробей

Ведение математических записей

Округление натуральных чисел 5 класс

Дробь — знак деления

Дроби — коротко о главном

Умножение десятичных дробей на 10, 100, 1000

Применение целых чисел

Основные понятия

Числитель и знаменатель

Операции над дробями

Сложение

Вычитание

Умножение

Деление

Сокращение

Вопросы и ответы

Какие дроби называются простыми?

Что такое степени с дробями?

Как пользоваться калькулятором дробей?

Похожие калькуляторы

Действия с десятичными дробями

Как складывать десятичные дроби

Представление дроби в виде числа

Специфика работы с многоэтажными дробями

Похожие записи:

Похожие записи: