Что такое отношение чисел

Зачем нужно отношение двух чисел в математике?

Отношение двух чисел — это понятие, которое имеет большое значение в математике и ее приложениях. Оно позволяет нам сравнивать, сопоставлять и анализировать числовые значения и взаимодействие между ними.

Основное назначение отношения двух чисел в математике:

• Сравнение и упорядочение: Отношение чисел позволяет нам сравнивать и упорядочивать их значения. Например, отношение «больше» позволяет нам сказать, что одно число больше другого. Это возможно благодаря отношению, которое определено на множестве чисел.
• Пропорции и соотношения: Отношение чисел также часто используется для выражения пропорций и соотношений между различными величинами. Например, можно сказать, что одно число в определенное количество раз больше или меньше другого числа. Это позволяет нам описывать соотношение между величинами и решать задачи, связанные с пропорциональностью.
• Анализ данных: В математике отношение чисел используется для анализа данных и статистики. Оно позволяет нам сравнивать и оценивать числовые характеристики, такие как среднее значение, медиана и другие. Отношение чисел также используется для определения процентного соотношения, которое позволяет нам анализировать структуру и изменения в данных.

Отношение двух чисел не только позволяет нам сравнивать и анализировать значения, но и обеспечивает основу для дальнейшего развития математических концепций. Оно широко используется в алгебре, геометрии, теории вероятности и других областях математики, а также в нашей повседневной жизни, где мы сталкиваемся со сравнениями, пропорциями и анализом данных.

Упражнения

Китайская энциклопедия

Борхес в одном из своих произведений приводит отрывок из таинственной китайской энциклопедии. Это «божественное хранилище благотворных знаний» говорит, что «животные подразделяются на: а) принадлежащих Императору, б) бальзамированных, в) прирученных, г) молочных поросят, д) сирен, е) сказочных, ж) бродячих собак, з) включенных в настоящую классификацию, и) буйствующих, как в безумии, к) неисчислимых, л) нарисованных очень тонкой кисточкой из верблюжьей шерсти, м) и прочих, п) только что разбивших кувшин, о) издалека кажущихся мухами» (Борхес Х.Л. Аналитический язык Джона Уилкинса // Соч. в 3 т. Т. 2. Рига: Полярис, 1997, с. 85).

Попробуйте представить эту классификацию животных в виде дерева. Считаете ли вы, что она выполнена правильно? Если да, то докажите, что ни одно из правил деления в ней не нарушено. Если нет, то объясните, какие именно правила нарушены. Каким образом эту классификацию можно было бы исправить?

Мясо не еда

Кот. Прости, пожалуйста, за нескромность. Я тебя давно вот о чем хотел спросить…

Осел. Ну?

Кот. Как можешь ты есть колючки?

Осел. А что?

Кот. В траве попадаются, правда, съедобные стебельки. А колючки… сухие такие!

Осел. Ничего. Люблю острое.

Кот. А мясо?

Осел. Что – мясо?

Кот. Не пробовал есть?

Осел. Мясо – это не еда. Мясо – это поклажа. Его в тележку кладут, дурачок. (Е. Шварц, «Дракон»)

Определите отношения между понятиями «еда», «острые предметы», «острая еда», «колючки», «мясо» и «поклажа». Изобразите эти отношения с помощью графических схем. Помните, что понятия могут быть сравнимы, только если они принадлежат к одному универсуму рассмотрения.

Разговор мужа с женой

Муж: Милая, ты не права.

Жена: Ах, я не права. Значит, я лгу. Я лгу, значит, я плохой человек, то есть нелюдь. Ты хочешь сказать, что я животное? Мама, он меня скотиной назвал!

Определите, правильно ли был выполнен переход между понятиями «человек, который не прав», «лжец», «плохой человек», «нелюдь», «животное», «скотина». Обоснуйте свою позицию. Какие операции над понятиями использовались при этом переходе? В каких отношениях находятся эти понятия? Изобразите их с помощью графических схем.

Отношение двух чисел

Определение 1

Отношением двух чисел является их частное.

Пример 1

• отношение $18$ к $3$ может быть записано как:

  $18\div 3=\frac{18}{3}=6$.

• отношение $5$ к $15$ может быть записано как:

  $5\div 15=\frac{5}{15}=\frac{1}{3}$.

С помощью отношения двух чисел можно показать:

• во сколько раз одно число превышает другое;
• какую часть представляет одно число от другого.

При составлении отношения двух чисел в знаменателе дроби записывают то число, с которым проводится сравнение.

Чаще всего такое число следует после слов «по сравнению с …» или предлога «к …».

Вспомним основное свойство дроби и применим его к отношению:

Замечание 1

При умножении или делении обоих членов отношения на одно и то же число, отличное от нуля, получаем отношение, которое равно исходному.

Рассмотрим пример, который иллюстрирует использование понятия отношения двух чисел.

Пример 2

Количество осадков в предыдущем месяце составляло $195$ мм, а в текущем месяце – $780$ мм. Во сколько раз увеличилось количество осадков в текущем месяце по сравнению с предыдущим месяцем?

Решение.

Составим отношение количества осадков в текущем месяце к количеству осадков в предыдущем месяце:

$\frac{780}{195}=\frac{780\div 5}{195\div 5}=\frac{156\div 3}{39\div 3}=\frac{52}{13}=4$.

Ответ: количество осадков в текущем месяце в $4$ раза больше, чем в предыдущем.

Пример 3

Найти сколько раз число $1 \frac{1}{2}$ содержится в числе $13 \frac{1}{2}$.

Решение.

$13 \frac{1}{2}\div 1 \frac{1}{2}=\frac{27}{2}\div \frac{3}{2}=\frac{27}{2} \cdot \frac{2}{3}=\frac{27}{3}=9$.

Ответ: $9$ раз.

Интересные сведения из истории возникновения математики

Откуда же взялась математика? Куда же уходит корнями история развития математики? Самым первым источником появления простейшей математики ученые считают пальцы на руках и ногах, а также различные части тела. Об этом свидетельствует множество наскальных рисунков, дошедших до нашего времени. Учеными установлено, что 6 тысяч лет назад древние вавилоняне уже использовали простые математические действия: для бытовых нужд, учета скота, подсчета количества урожая, размера прибыли и расходов, при совершении купли или продажи различных товаров. Позже они же первые упоминают о решении математических задач и уравнений повышенной сложности. К самым первым математическим открытиям относят возникновение математических действий, которые известны нам как сложение, вычитание, умножение и деление.

Ученые-историки до сих пор спорят о точной дате появления этой науки и о месте, где впервые она появилась. Конкурентами в этом споре выступают древний Вавилон и Египет. Самые первые подтверждения математической деятельности принадлежат Свазиленду. Там найдены кости бабуинов с нанесенными черточками, которые явно говорят о первых математических операциях, выполненных 40000 лет назад.

()

А когда же появились дроби? Упоминания о дробях возникли гораздо позже, но уже достоверно известно, что жители древнего Египта совершали операции с дробями, у которых числителем являлась единица.

А вот представление о десятичных дробях появилось всего лишь пять столетий назад, а в Европу попало только через 200 лет после появления.

 (И)

Невероятные факты, связанные с математикой:

• Всю математическую науку возможно записать в сто тысяч томов;
• Центилион — самое большое известное число, содержащее шестьсот нулей;
• Наименьшее число используется только в астрономии. Названия не имеет. Записывается дробью; после запятой имеет сто миллионов триллионов нулей, а в конце единицу;
• Самая магическая цифра, которая таит множество суеверий — 666. В Европейской палате все время пустует только одно кресло под номером 666. Во всем мире люди стараются не использовать это число. Такой номер не присваивается телефонным кодам, автобусам,трассам или поездам;
• В Китае самым суеверным числом считают число 4. При этом, такой номер не присваивается домам, квартирам, нет даже 4 этажа.

Математика очень дружна со всеми существующими науками, видами деятельности и профессиями. Одно мудрое выражение гласит «Математика-язык других наук». Поспорить с этим очень сложно, ведь она является основой для развития таких дисциплин:

• Химия;
• Физика;
• Астрономия;
• Биология;
• История;
• Экономика;
• География;
• Информатика;
• Политология;
• Музыка;
• Литература.

Теперь мы можем с уверенностью сказать, что знание математики — залог вашей успешности и развития не только в будущем, а уже сегодня!

Что нужно знать об отношении двух чисел в математике за 6 класс

Отношение чисел является частным данных чисел.

Запись отношения принято обозначать с помощью арифметического действия деления. Также допускается представление отношения в виде обыкновенной дроби:

Здесь записано отношение чисел a и b. Число а может называться предыдущим членом, b играет роль последующего члена.

Запись отношения пары чисел таких, как 75 и 25, имеет вид:

75 : 25 = 75 25 = 3

С помощью объяснения отношения можно выразить следующее:

• во сколько раз первое число больше по сравнению со вторым;
• какую часть первое число составляет от второго числа.

При решении задач на уроках по математике в шестом классе на тему «Отношение чисел» можно часто встретить примеры с процентами

Поэтому важно ознакомиться с особенностью понятия процентного соотношения и записать его в конспект

Вычислить процентное отношение пары чисел можно путем деления одного числа на второе, а полученный результат следует умножить на 100.

Даны два числа: 52 и 400. Требуется определить, сколько процентов составляет первое число от второго числа. Воспользуемся правилом вычисления процентного соотношения и запишем:

52 : 400 · 100 % = 13 %

Подобные отношения можно найти в заданиях, где по условию определены некие величины, и требуется вычислить их процентное соотношение. Знание определенных правил вычисления поможет значительно упростить решение. Среди вопросов могут быть такие:

• на сколько процентов была перевыполнена работа;
• на сколько процентов готов результат;
• указать повышение или снижение цены товара в процентах

и другие вопросы, в которых присутствует понятие «процент».

Свойства отношения чисел

В том случае, когда имеется пара чисел или значений одинаковой величины, обозначенных как a и b, справедливы следующие соотношения:

• отношение a к b является результатом частного a и b;
• когда a>b, отношение a:b говорит о том, во сколько раз число a больше по сравнению с b;
• когда a<b, отношение a:b говорит о том, что a является некой частью от b;
• процентное отношение a к b представляет собой отношение a:b, которое умножили на 100%.

Ключевое свойство частного: частное сохраняется без изменений в том случае, когда делимое и делитель умножают или делят на одинаковое число.

Основное свойство частного позволяет вывести главное свойство отношения.

Основное свойство отношения: при умножении или делении членов какого-то отношения на одинаковое число, которое не равно нулю, данное отношение сохранится без изменений.

Примеры решения задач с пояснениями

Месячный план производства равен 1200 изделий. В результате предприятие произвело 2300 изделий. Требуется определить процент превышения плана.

Данную задачу можно решить двумя способами. Рассмотрим их по отдельности.

Способ 1. Запишем, что 1200 изделий являются планом, то есть составляют 100 %. Определим, количество изделий, изготовленных больше плана:

Вычислим разницу между фактом и планом в процентах:

1100 от 1200 ⇒ 1100 : 1200 · 100 % = 91 , 7 % .

Попробуем выполнить вычисления другим методом.

Способ 2. Сначала найдем разницу между планом и фактом в процентах:

2300 от 1200 ⇒ 2300 : 1200 · 100 % = 191 , 7 % .

Далее определим процент перевыполнения плана:

191 , 7 % — 100 % = 91 , 7 % .

Поставлена задача вспахать землю на участке поля площадью 500 га. В течение первого дня было обработано 150 га почвы. Требуется вычислить, сколько процентов удалось вспахать от общего запланированного объема.

Найдем отношение обработанной земли к общей площади поля и запишем результат в процентном выражении:

150 : 500 · 100 % = 150 500 · 100 % = 3 10 · 100 % = 0 , 3 · 100 % = 30 % .

Производительность мастера составила 45 деталей, а по плану требовалось изготовить 36 деталей. Нужно найти процент фактически проделанной работы от планируемого объема.

Здесь вычислим отношения чисел и запишем результат в процентном выражении:

45 : 36 · 100 % = 1 , 25 · 100 % = 125 %

Задания для самостоятельной работы

Должность председателя желали занять два претендента. Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель.

Отношение количества хвойных деревьев к лиственным в лесу можно выразить как 1:4. Нужно вычислить процент лиственных деревьев.

Сельскохозяйственные растения высаживают на площади 24 Га. Зерновые культуры и овощные распределены в соответствии с отношением 5:3. Необходимо вычислить площадь в Га, которую занимают овощные культуры.

Разряды и разрядность

Обратимся к табл. 4.6 и выпишем ряд десятичных чисел, которые равны “круглым” двоичным числам. В этот ряд входят следующие десятичные числа: “2”, “4”, “8”, “16”, “32”, “64”, “128”, “256”, “512” и, наконец, сакраментальное “1024”. Все эти числа представляют ряд последовательных степеней числа “2”. Каждое из названных чисел чрезвычайно активно используется в компьютерных технологиях. Читатель, видимо, убеждался в этом не один раз.

Мы оперируем каким-либо двоичным числом, а любое двоичное число – это совокупность битов, т. е. “1” и “0”. Отсюда получается, что каждый бит – это один разряд или одна позиция в двоичном числе.

ЗамечаниеНадеемся, что вы еще не забыли о позиционном принципе записи чисел в любых математических системах счисления (значение цифр, количество которых ограничено, зависит от положения в числе, от ее позиции).

В данный момент мы делаем шаг в сторону абстрагирования от конкретных значений цифр и начинаем считать только количество знакомест (позиций), которое в математике принято называть “разрядом”, а совокупность разрядов (знакомест) – “разрядностью”.

Определение

Разряд в арифметике – это место, занимаемое цифрой при записи числа. Например, в десятичной системе счисления цифры первого разряда – это единицы, второго разряда – десятки и т. д.

Но арифметические законы, которые кажутся привычными в десятичной системе счисления, все без исключения действительны и для двоичной системы счисления. Двоичные числа также можно складывать, вычитать, перемножать и делить с использованием тех же приемов школьного курса арифметики. Отличие заключается только в том, что используются всего две цифры.

Кроме того, как мы уже выяснили, в двоичной системе счисления каждый разряд – это бит и его значение зависит от позиции и равно соответствующей степени числа “2”.

Определение

Разрядность двоичного числа – это количество знакомест (разрядов) или количество битов, заранее отведенных для записи числа.

Пример

Десятичное число “2” может быть записано различными способами в зависимости от разрядности двоичного числа: как “10”, если разрядность равна двум; как “0010”, если разрядность равна четырем; как “00000010”, если разрядность равна восьми

Обратите внимание, что последний вариант соответствует записи десятичного числа “2” в пределах одного байта информации

Разрядность двоичного числа интересует нас в связи с тем, что это количество разрядов (позиций или знакомест) обеспечивает определенный набор возможных двоичных чисел, которые, как мы уже договорились, могут служить кодами, с помощью которых происходит кодирование любых видов информации: собственно чисел, текстов, графических и цветных изображений, звуков, анимации и видео.

Осталось только выяснить, каким образом разрядность влияет на количество информации (двоичных кодов), которую можно получить с помощью определенного количества разрядов. Однако прежде следует учесть одну особенность двоичных чисел, нашедшую применение в компьютерных технологиях, – это фиксированные значения разрядности двоичных чисел.

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример:

1. А = {а, в, с, у} – А состоит из четырех элементов.
2. Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

• конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
• бесконечные — не являющиеся конечными (например, числовые);
• пустые (обозначаются Ø) – не имеющие элементов.

Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.

Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.

Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

F = { Том, Джон, Лео }

Пример 2. Запишем множество делителей числа 6.

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

D = { 1, 2, 3, 6 }

Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:

2 ∈ D

Читается как «2 принадлежит множеству делителей числа 6»

Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:

5 ∉ D

Читается как «5 не принадлежит множеству делителей числа 6»

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

{ Том }

Зададим множество, которое состоит из одного числа 2

{ 2 }

Зададим множество, которое состоит из двух чисел: 2 и 5

{ 2, 5 }

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.

N = {9, 11, 13, 15……}.

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Z = {-112, -60, -25, 0, 36, 58, 256}.

Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

5 = 5/1 = 10/2 = 25/5;

0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

Вернемся к отношению девочек к мальчикам (10 : 5). Данное отношение показало, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.

В нашем примере удобнее разделить члены отношения  на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

В обоих классах девочек  в два раза больше мальчиков, поскольку отношения    и    равны одному и тому же числу.

Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

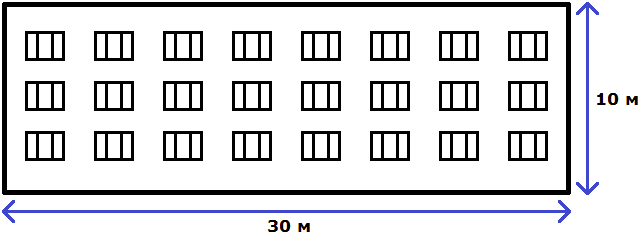
Чтобы нарисовать на бумаге похожий дом, нужно рисовать его в таком же отношении 30 : 10.

Разделим оба члена этого отношения на число 10. Тогда получим отношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1  м = 100 см

Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

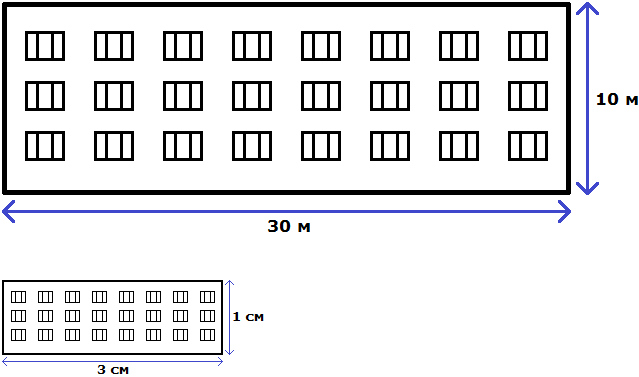
Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части

40 м : 4 = 10 м

Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.

Определим сколько метров приходится на ширину:

10 м × 3 = 30 м

Определим сколько метров приходится на высоту:

10 м × 1 = 10 м

Практика Расчет соотношений с двумя величинами

Практикуйтесь в выявлении реальных возможностей выражения соотношений путем нахождения величин, которые вы хотите сравнить. Затем вы можете попробовать вычислить эти отношения и упростить их до наименьших целых чисел. Ниже приведены несколько примеров подлинных соотношений для практики вычислений.

1. В миске с 8 кусочками фруктов 6 яблок.
   1. Каково соотношение яблок к общему количеству фруктов? (ответ: 6: 8, упрощенный до 3: 4)
   2. Если два фрукта, не являющиеся яблоками, являются апельсинами, каково соотношение яблок и апельсинов? (ответ: 6: 2, упрощенный до 3: 1)
2. Д-р. Пастбище, сельский ветеринар, лечит всего 2 вида животных – коров и лошадей. На прошлой неделе она пролечила 12 коров и 16 лошадей.
   1. Каково соотношение коров к лошадям, которых она лечила? (ответ: 12:16, упрощенный до 3: 4. На каждые 3 обработанных коровы приходилось лечить 4 лошади)
   2. Каково отношение коров к общему количеству животных, которых она лечила? (ответ: 12 + 16 = 28, общее количество обработанных животных. Отношение коров к общему количеству составляет 12:28, упрощенное до 3: 7. На каждые 7 обработанных животных 3 из них были коровами)

Понятие отношения в математике: что это?

В математике отношение представляет собой связь между двумя или более элементами. Оно описывает, какие характеристики или свойства присутствуют у объектов и как они связаны друг с другом. Отношения широко применяются в различных областях математики, начиная от алгебры и геометрии, и заканчивая теорией вероятностей и статистикой.

В математике отношения можно представить в виде таблицы, называемой таблицей отношений. Эта таблица содержит две строки и несколько столбцов. В первой строке указываются элементы из множества A, а во второй строке указываются элементы из множества B. В клетках таблицы отмечается, присутствует ли отношение между соответствующими элементами множеств A и B.

Отношения могут быть разных типов. Наиболее часто встречающиеся типы отношений:

• Отношения эквивалентности: это отношения, которые обладают свойствами рефлексивности, симметричности и транзитивности. Например, отношение «равно» является отношением эквивалентности, так как оно удовлетворяет этим свойствам.
• Отношения порядка: это отношения, которые определяют упорядоченность элементов множества. Например, отношение «больше» является отношением порядка на множестве натуральных чисел.
• Отношения функций: это отношения, где каждому элементу из одного множества соответствует ровно один элемент из другого множества. Отношение «является предком» в генеалогическом дереве является примером отношения функций.

Отношения в математике имеют важное практическое применение. Они используются для моделирования и анализа различных явлений в науке, экономике, социологии и других областях

Отношения также являются основой для различных математических структур, таких как графы и матрицы, которые широко применяются в компьютерных науках и информационных технологиях.

Примеры нахождения отношения чисел

Отношение двух чисел выражает, какое количество раз первое число содержится во втором. Например, если мы имеем число 4 и число 12, то отношение чисел будет 4:12 или 1:3. Это означает, что 4 содержится в 12 три раза.

Если числа имеют разную размерность, например, одно выражено в метрах, а другое в сантиметрах, то нужно сначала привести числа к одной размерности. Для этого можно использовать соответствующие формулы преобразования единиц измерения.

Отношение чисел может быть не только целым, но и дробным. Например, 1/2, 7/3 или 10/7

При этом, следует обратить внимание на то, что дробное число можно привести к целому, умножив его на некоторую константу, например, при 1/2 он будет равен 0,5, а умножив его на 10, получим 5

Отношение можно найти не только для двух чисел, но и для любого их количества. Например, при определении соотношения прироста населения страны можно использовать данные о количестве родившихся и умерших за определенный промежуток времени.

Пример нахождения отношения двух чисел

Первое число	Второе число	Отношение чисел
4	12	1:3
7,5 кг	7500 г	1:1000
3/4	1	3:4

В таблице приведены примеры нахождения отношения чисел. Первое число находится в первом столбце, второе число во втором. Отношение чисел вычисляется и записывается в третьем столбце.

Вопрос-ответ

Вопрос: Как найти отношение двух дробей?

Ответ: Для того, чтобы найти отношение двух дробей, нужно поделить первую дробь на вторую. Например, если нужно найти отношение 2/3 к 4/5, нужно выполнить следующее действие: 2/3 : 4/5 = 2/3 * 5/4 = 10/12 = 5/6. Таким образом, отношение 2/3 к 4/5 равно 5/6.

Вопрос: Как найти отношение двух вещественных чисел?

Ответ: Для того, чтобы найти отношение двух вещественных чисел, нужно поделить первое число на второе. Например, если нужно найти отношение 2.5 к 3.5, нужно выполнить следующее действие: 2.5 / 3.5 = 0.7142857. Таким образом, отношение 2.5 к 3.5 равно 0.7142857.

Вопрос: Как найти отношение произвольных чисел?

Ответ: Для того, чтобы найти отношение произвольных чисел, нужно поделить первое число на второе. Например, если нужно найти отношение 15 к 7, нужно выполнить следующее действие: 15 / 7 = 2.142857. Таким образом, отношение 15 к 7 равно 2.142857.

Вопрос: Какая формула для нахождения отношения чисел?

Ответ: Формула для нахождения отношения чисел очень проста — это деление первого числа на второе. Например, если нужно найти отношение 10 к 5, то формула будет следующей: 10 / 5 = 2. Таким образом, отношение 10 к 5 равно 2.

Вопрос: Как работает отношение чисел в математике?

Ответ: Отношение чисел — это показатель того, как одно число связано с другим. Например, если первое число в два раза больше второго, то отношение первого числа к второму будет 2:1. Отношение чисел используется во многих областях математики, в том числе в алгебре и геометрии. Оно может быть использовано для определения пропорции, нахождения процентов и дробей, а также для решения уравнений и построения графиков.

Главная — Полезно — Узнайте, как легко найти отношение чисел: простые шаги и подсказки

Комментарии

PinkPenguin

5.0 out of 5.0 stars5.0

Читала статью «как найти отношение чисел» и осталась довольна. Автор очень понятно объяснил, что такое отношение чисел и как его найти. Пригодится в жизни, чтобы лучше понимать некоторые задачи на математику. Единственное, хотелось бы больше примеров и задач для практики.

Дмитрий Баранов
5.0 out of 5.0 stars5.0

Статья очень просто и понятно объясняет, как найти отношение чисел. Благодарю!

Nick123
5.0 out of 5.0 stars5.0

Анастасия
5.0 out of 5.0 stars5.0

Статья очень полезная для меня! Теперь я знаю, как найти отношение чисел.

Алексей Сидоров
5.0 out of 5.0 stars5.0

Я часто сталкиваюсь с задачами, где нужно вычислить отношение двух чисел. Эта статья мне очень помогла, теперь я точно знаю, как это делать. Единственное, что может быть немного сложно для начинающих — это использование дробей. Но, в целом, статья написана доступно и понятно. Рекомендую к прочтению!

Мария
5.0 out of 5.0 stars5.0

Не секрет, что многие люди испытывают сложности с математикой и поэтому статья «как найти отношение чисел» вызвала у меня большой интерес. На мой взгляд, автор очень хорошо описал эту тему, не забывая упомянуть про различные способы нахождения отношения чисел и как с этим работать. Но я бы предложила добавить небольшой раздел с примерами и задачами для практики. Это бы сделало статью еще более полезной и помогло бы читателям лучше усвоить материал. В целом, статья порадовала и я буду рекомендовать её своим знакомым, которые также встречаются с трудностями в этом вопросе.

Пропорции

Если два или более количества, состоящих в пропорциональном соотношении, являются всеми количествами, задействованными в конкретной ситуации, например, два яблока и три апельсина в корзине, в которой нет других фруктов, то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае, 25{\displaystyle {\tfrac {2}{5}}}, или 40 % целого, — это яблоки, а 35{\displaystyle {\tfrac {3}{5}}}, или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.

Другие применения

• Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
• Шансы выигрыша в играх выражают в виде соотношения.
• Возможны соотношения количеств, измеряемых в разных единицах измерения.

Отношение порядка

Отношение R, обладающее свойствами рефлексивности, антисимметричности и транзитивности, называется отношением порядка. Если на данном множестве введено отношение порядка, то это множество называется упорядоченным. В этом случае вместо пишут Множество совершенно упорядочено, если для любых двух элементов и из множества М

имеет место либо , либо В противном случае говорят, что множество частично упорядочено. Например, отношение «быть выше» на множестве деревьев — совершенно упорядочено, а отношение «быть делителем» на множестве целых чисел — частично упорядочено.

Пусть каждому элементу из множества М по некоторому правилу f поставлено в соответствие вещественное число вес элемента . Введение веса для каждого элемента позволяет упорядочить их по мере возрастания (убывания) весов, а затем сравнивать элементы в соответствии с присвоенным весом. Примерами упорядочения посредством введения весов являются: присвоению каждому товару его цены, каждому станку его надежности, каждому телу его веса, объема и т.п. Взвешивание вариантов решений посредством формирования комплексного показателя качества является одним из самых распространенных способов решения проблемы выбора на множестве разнокачественных признаков.

Если отношение обладает свойствами антирефлексивности, асимметричности и транзитивности, то оно называется отношением строгого порядка (обозначается ). Примером отношения строгого порядка является порядок букв в фиксированном алфавите. Упорядочение букв в алфавите позволяет, в свою очередь, упорядочить слова в словарях (лексикографическое упорядочение слов).