Вычисление определителя матрицы методом Гаусса.
Опишем суть этого метода. Матрица А с помощью элементарных преобразований приводится к такому виду, чтобы в первом столбце все элементы, кроме стали нулевыми (это сделать всегда возможно, если определитель матрицы А отличен от нуля). Эту процедуру опишем чуть позже, а сейчас поясним, для чего это делается. Нулевые элементы получаются для того, чтобы получить самое простое разложение определителя по элементам первого столбца. После такого преобразования матрицы А, учитывая восьмое свойство и , получим
где — минор (n-1)-ого порядка, получающийся из матрицы А вычеркиванием элементов ее первой строки и первого столбца.
С матрицей, которой соответствует минор , проделывается такая же процедура получения нулевых элементов в первом столбце. И так далее до окончательного вычисления определителя.
Теперь осталось ответить на вопрос: «Как получать нулевые элементы в первом столбце»?
Опишем алгоритм действий.
Если , то к элементам первой строки матрицы прибавляются соответствующие элементы k-ой строки, в которой . (Если все без исключения элементы первого столбца матрицы А нулевые, то ее определитель равен нулю по второму свойству и не нужен никакой метод Гаусса). После такого преобразования «новый» элемент будет отличен от нуля. Определитель «новой» матрицы будет равен определителю исходной матрицы в силу седьмого свойства.
Теперь мы имеем матрицу, у которой . При к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на . И так далее. В заключении к элементам n-ой строки прибавляем соответствующие элементы первой строки, умноженные на . Так будет получена преобразованная матрица А, все элементы первого столбца которой, кроме , будут нулевыми. Определитель полученной матрицы будет равен определителю исходной матрицы в силу седьмого свойства.
Разберем метод при решении примера, так будет понятнее.
Пример.
Вычислить определитель матрицы порядка 5 на 5 .
Решение.
Воспользуемся методом Гаусса. Преобразуем матрицу А так, чтобы все элементы ее первого столбца, кроме , стали нулевыми.
Так как изначально элемент , то прибавим к элементам первой строки матрицы соответствующие элементы, например, второй строки, так как :
Знак « ~ » означает эквивалентность.
Теперь прибавляем к элементам второй строки соответствующие элементы первой строки, умноженные на , к элементам третьей строки – соответствующие элементы первой строки, умноженные на , и аналогично действуем вплоть до шестой строки:
Получаем
С матрицей проводим ту же процедуру получения нулевых элементов в первом столбце:
Следовательно,
Сейчас выполняем преобразования с матрицей :
Получаем
Матрица уже имеет необходимый вид, поэтому
Ответ:
.
Рассмотрим решение еще одного примера, но подробно описывать действия не будем. Это некоторый образец краткой записи вычисления определителя матрицы методом Гаусса.
Пример.
Вычислите определитель матрицы порядка 7 на 7.
Решение.
Следовательно,
Замечание.
На некотором этапе преобразования матрицы по методу Гаусса может возникнуть ситуация, когда все элементы нескольких последних строк матрицы станут нулевыми. Это будет говорить о равенстве определителя нулю.
Подведем итог.
Определителем квадратной матрицы, элементы которой есть числа, является число. Мы рассмотрели три способа вычисления определителя:
- через сумму произведений сочетаний элементов матрицы;
- через разложение определителя по элементам строки или столбца матрицы;
- методом приведения матрицы к верхней треугольной (методом Гаусса).
Были получены формулы для вычисления определителей матриц порядка 2 на 2 и 3 на 3.
Мы разобрали свойства определителя матрицы. Некоторые из них позволяют быстро понять, что определитель равен нулю.
При вычислении определителей матриц порядка выше 3 на 3 целесообразно использовать метод Гаусса: выполнить элементарные преобразования матрицы и привести ее к верхней треугольной. Определитель такой матрицы равен произведению всех элементов, стоящих на главной диагонали.
Некогда разбираться?
Матричный ранг
Ранг матрицы — это оценка количества линейно независимых строк или столбцов в матрице.
Ранг матрицы M часто обозначается как функция rank ().
Интуиция для ранга состоит в том, чтобы считать его числом измерений, охватываемых всеми векторами в матрице. Например, ранг 0 предполагает, что все векторы охватывают точку, ранг 1 предполагает, что все векторы охватывают линию, ранг 2 предполагает, что все векторы охватывают двумерную плоскость.
Ранг оценивается численно, часто с использованием метода матричной декомпозиции. Распространенным подходом является использование разложения по сингулярному значению или SVD для краткости.
NumPy предоставляет функцию matrix_rank () для вычисления ранга массива. Он использует метод SVD для оценки ранга.
В приведенном ниже примере показано вычисление ранга матрицы со скалярными значениями и другого вектора со всеми нулевыми значениями.
При выполнении примера печатается первый вектор и его ранг 1, за которым следует второй нулевой вектор и его ранг 0.
Следующий пример проясняет, что ранг — это не количество измерений матрицы, а число линейно независимых направлений.
Представлены три примера матрицы 2 × 2, демонстрирующие матрицы с рангом 0, 1 и 2.
При выполнении примера сначала печатается матрица 0 2 × 2, за которой следует ранг, затем матрица 2 × 2 с рангом 1 и, наконец, матрица 2 × 2 с рангом 2.
2.3. Определители
Каждой квадратной матрице по определённому правилу
можно поставить в соответствие единственное число.Это число называется определителем и
символически обозначается
.
Порядок определителя равен порядку квадратной матрицы.
Определитель
второго порядка вычисляется следующим образом
,(2)
т.е.из произведения элементов, стоящих на так
называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний
угол), вычитается произведение элементов, находящихся напобочной диагонали (идущей из левого нижнего
в правый верхний угол).
П р и м е р. Вычислите определитель матрицы .
Р
е ш е н и е. Значения элементов
матрицы ,т.е.
Подставляем
в формулу (2) и получаем
.
Определитель
третьего порядка вычисляется с помощью формулы
(3)
З а м е ч а н и е.Чтобы легче
запомнить эту формулу, можно использовать так называемое правило треугольников
(правило Саррюса). Оно заключается в следующем. Элементы, произведения которых входят
в определитель со знаком «+», располагаются на главной диагонали и в вершинах
треугольников,симметричных относительно
главной диагонали
Элементы,
произведения которых входят в определитель со знаком «–», располагаются
аналогичным образом относительно побочной диагонали
П р и м е р. Вычислите определитель матрицы .
Р е ш е н и е. Подставляем значения элементов матрицы в формулу (3) и находим
величину заданного определителя
Для вычисления определителей третьего
порядка можно пользоваться ещёправилом «35». Согласно этому правилу к заданной матрице
добавляют
ещё первые два столбца
.
Элементы, произведения которых входят в определитель
со знаком «+», располагаются на главной диагонали и на отрезках, параллельных
главной диагонали
.
Элементы, произведения которых входят в определитель
со знаком «–», располагаются на побочной диагонали и на отрезках, параллельных
побочной диагонали
.
Определитель
равен сумме указанных
произведений элементовс учетом их
знаков.
Основные
свойства определителей
Рассмотрим основные свойства определителей 2-го и 3-го
порядка
С в о й с т в о1. Определитель не
изменяется при транспонировании, т.е.
.(4)
Действительно,
,
=,
Из чего следует
справедливость равенства (4).
Из свойства 1
следует, чтосвойствами определителей,
сформулированные для строк будут такими же как и для столбцов. Поэтомуследующие свойства определителей будут формулироваться
только для строк.
С в о й с т в о 2. При умножении элементов строки определителя на
некоторое числоопределитель умножается
на это число, т.е.
В справедливости этого свойства можно убедиться,
вычислив эти определители
Свойство 3.
Определительравен нулю в следующих
случаях:
a)одна из строк
нулевая
,
б) две равные строки
в)элементы
двух строкпропорциональны
В
справедливости перечисленных свойств легко убедиться с помощью формулы (3).
С в о й с т в о 4. Если две какие-либо строки определителя поменять
местами, то знак определителя изменится на противоположный
Доказательство
этого свойства выполняется с помощью формулы (3).
С в о й с т в о5. Еслив
определителе некоторая строка, например, первая является линейной
комбинациейдвух строк с коэффициентами и
,
то определитель будет
равен сумме двух определителей, определяемых формулой
Справедливость
этого свойства можно доказать, сравнив значения левой и правой частей
равенства, найденные с помощью формулы (3).
С в о й с т в о6. Величина определителя
не изменится, если к элементам одной строки прибавить соответствующие элементы
другой строки, умноженные на одно и то же число
Алгоритм и шаги
Транспонирование матрицы — это процесс, при котором столбцы и строки матрицы меняются местами. В результате этого процесса матрица превращается в новую матрицу, в которой элементы, ранее находившиеся в строках, теперь находятся в столбцах, а элементы, ранее находившиеся в столбцах, теперь находятся в строках.
Чтобы произвести транспонирование матрицы, нужно выполнить следующие шаги:
- Определить размерность матрицы — количество строк и столбцов;
- Создать новую матрицу, размерность которой будет равна транспонированной матрице. Если исходная матрица имеет n строк и m столбцов, то транспонированная матрица будет иметь m строк и n столбцов;
- Скопировать элементы из исходной матрицы в новую матрицу так, чтобы элементы, находившиеся в i-й строке и j-м столбце исходной матрицы, находились в j-й строке и i-м столбце новой матрицы;
- Вывести полученную транспонированную матрицу.
Пример транспонирования матрицы:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
Транспонированная матрица:
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
В результате транспонирования матрицы столбцы и строки поменялись местами, и элементы, ранее находившиеся в строках, теперь находятся в столбцах, а элементы, ранее находившиеся в столбцах, теперь находятся в строках.
Добавление двух матриц
Мы добавим две матрицы и, используя вложенный цикл for, пройдемся по заданным матрицам.
Пример –
mat1 = ,
,
]
mat2 = ,
,
]
mat3 = ,
,
]
matrix_length = len(mat1)
#To Add mat1 and mat2 matrices
for i in range(len(mat1)):
for k in range(len(mat2)):
mat3 = mat1 + mat2
#To Print the matrix
print("The sum of Matrix mat1 and mat2 = ", mat3)
Выход:
The sum of Matrix M1 and M2 = , , ]
Объяснение:
- Первая и вторая матрицы – 3×3.
- Мы инициализировали еще одну матрицу mat3, в которой будет храниться равнодействующая матрица.
- Применили вложенный цикл for для перебора матриц, внешний цикл перебирает первую матрицу.
- Управление передается во внутренний цикл; затем переходит ко второму внутреннему циклу, здесь значение i равно нулю, и k также равно нулю.
- В первой итерации первые элементы mat1 и mat2, добавленные друг к другу, будет продолжаться до тех пор, пока не будут добавлены все элементы.
Как транспонировать матрицу?
Транспонирование матрицы – это простой способ изменить расположение элементов матрицы относительно ее основной диагонали. Другими словами, строки матрицы становятся ее столбцами, а столбцы – строками.
Для транспонирования матрицы необходимо пройти по ее элементам и поменять их индексы местами:
- Элемент становится ;
- Матрица размером MxN превращается в NхM матрицу.
Также можно представить процесс транспонирования с использованием временной матрицы. В этом случае, при перемещении элементов матрицы, их значения сохраняются в отдельную матрицу:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
Транспонированная матрица:
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
Транспонирование матрицы является важной операцией в математике и программировании и находит множество применений в различных алгоритмах и системах обработки данных
Симметричность и другие особенности
Транспонирование матрицы является одним из важных операций в линейной алгебре. Одной из основных особенностей транспонирования матрицы является ее симметричность. Если изначально матрица была симметричной относительно главной диагонали, то после транспонирования она также останется симметричной.
Кроме того, транспонирование матрицы позволяет осуществлять удобные операции с ее столбцами и строками. Например, транспонирование матрицы позволяет менять местами два столбца или две строки.
Транспонирование матрицы также используется в решении систем линейных уравнений. Для того, чтобы найти обратную матрицу, необходимо транспонировать ее и затем найти определитель. Если определитель не равен нулю, то обратная матрица существует.
Наконец, транспонирование матрицы позволяет удобно работать с матрицами, представляющими некоторые структуры данных. Например, матрица смежности в графах представляет собой квадратную матрицу, элементы которой равны 1, если между соответствующими вершинами графа есть ребро, и 0 в противном случае. Транспонирование матрицы смежности позволяет получить матрицу, которая показывает, на какие вершины графа есть входящие ребра для каждой вершины.
Что такое транспонированная матрица
Транспонированной матрицей называют такую матричную форму представления данных \(A^{T}\), которая образована из начальной A с помощью замещения строк столбцами.
С теоретической точки зрения, транспонированная матрица в случае с некоторой матричной формой А, обладающей размерностью \(m\times n\), сформирована как матрица под названием \(A^{T}\) со следующими габаритами: \(n \times m\), соответствующая такому выражению, которое можно вычислить:
\(A_`ij`^{T}=A_`ji`\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Пример 1
\({\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{{{\mathrm {T}}}}\!\!\;\!=\,{\begin{bmatrix}1&3\\2&4\end{bmatrix}} и {\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{{{\mathrm {T}}}}\!\!\;\!=\,{\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}\;\)
Исходя из данного определения и принципа построения матричных форм, можно прийти к выводу, что при записи транспонированной матрицы из начального массива данных, выстроенных в определенном порядке, строки нужно составить как колонки в аналогичной последовательности. Тогда получится необходимая матричная форма, которую далее можно решать при необходимости.
Умножение матриц Excel – voxt.
Объяснение
Умножение матриц — одна из полезных функций Excel, предназначенных для выполнения математических операций. Это помогает получить произведение двух матриц. Матрицы, которые нужно умножить, имеют определенное количество строк и столбцов для представления данных. Размер полученной матрицы берется из количества строк первого массива и количества столбцов второго массива. Есть условие умножения матриц; количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Для выполнения матричного умножения используется предопределенная функция MMULT, представленная в программном обеспечении Excel.
В общем, умножение матриц выполняется двумя способами. Простое скалярное умножение выполняется с использованием основных арифметических операций, а расширенное умножение матриц управляется с помощью функции массива в Excel.
Формула Excel, используемая для умножения, вводится двумя способами, включая ручной ввод функции MMULT после знака равенства или выбор библиотеки функций Math and Trig, представленной на вкладке «Формулы». Математическая функция MMULT помогает вернуть результат умножения двух массивов. Это одна из предопределенных функций Excel, используемых в рабочих таблицах для выполнения расчетов за короткое время.
Синтаксис
- Параметры: Array1 и Array2 — два параметра, необходимые для умножения.
- Правило: Столбцы массива array1 должны быть равны строкам array2, а размер продукта равен количеству строк в array1 и количеству столбцов в array2.
- Возврат: Функция MMULT генерирует числа в матрице продукта. Он вводится как формула или функция рабочего листа в вычислениях Excel.
Рассматривать,
Тогда произведение A * B выглядит следующим образом.
Как сделать умножение матриц в Excel? (с примерами)
Умножение матриц в Excel имеет некоторое приложение в реальном времени. Есть два способа выполнить матричное умножение. Ниже приведены несколько примеров умножения матриц Excel.
Вы можете скачать этот шаблон Excel для умножения матриц здесь — Шаблон для умножения матриц в Excel
Пример №1 — Умножение матрицы на скалярное число.
Шаг 1: В первую очередь необходимо ввести данные в массив.
Шаг 2: Выберите скалярное значение, которое мы собираемся умножить на массив, т.е. 3
-
Шаг 3: Оцените строки и столбцы результирующего массива.
Здесь результирующий массив будет размером 3 x 3. - Шаг 4: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат, и введите обычную формулу умножения.
Шаг 5: После ввода формулы нажмите Ctrl + Shift + Enter. И результат будет, как показано на нижеприведенном рисунке.
Пример # 2 — Матричное умножение двух отдельных массивов
Шаг 1: В первую очередь необходимо ввести данные в массив А размером 3 × 3.
Шаг 2: Введите данные во второй массив под названием B размером 3 × 3.
- Шаг 3: Нам нужно убедиться, что столбцы первого массива имеют такой же размер, как и строки второго массива.
Шаг 4: Оцените строки и столбцы результирующего массива.
Шаг 5: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат, и введите формулу умножения MMULT.
Введите значения, чтобы вычислить произведение A и B.
После ввода формулы нажмите Ctrl + Shift + Enter чтобы получить результат. Результаты получаются путем умножения двух массивов следующим образом, а размер результирующего массива составляет 3×3.
Пример # 3
Умножение матриц между массивами с одной строкой и одним столбцом. Рассмотрим элементы матриц как
Матрица A имеет размер 1 × 3, а матрица B — 3 × 1. Размер изделия А * Б матрица 1 × 1. Итак, введите в ячейку формулу умножения матриц.
Нажмите Enter, чтобы получить результат.
Матрица A имеет размер 3 × 1, а матрица B — 1 × 3. Размер изделия А * Б матрица 3 × 3.
Итак, ответ будет такой:
Пример # 5 — Определение квадрата матрицы с помощью MMULT в Excel
Квадрат матрицы A определяется умножением A на A.
Результирующая матрица получается как
Чтобы выполнить матричное умножение, количество столбцов, представленных в массиве 1, и количество строк, представленных в массиве 2, равны.
Изменить часть массива сложно, так как массив представляет собой группу элементов.
При выполнении умножения массива следует использовать CTRL + SHIFT + ENTER для создания всех элементов результирующей матрицы. В противном случае производится только один элемент.
Элементы массива не должны быть нулевыми, а текст не должен использоваться в матрицах, чтобы избежать ошибок.
Размер массива товаров равен строкам первого массива и столбцам второго массива.
Умножение A * B не равно умножению B * A в матричном умножении.
Умножение матрицы на единичную матрицу приводит к той же матрице (т.е. *знак равно)
Post Views: 848
Транспонирование матрицы
Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.
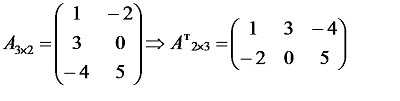
Что такое транспонированная матрица, в чем отличие от обычной
Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.
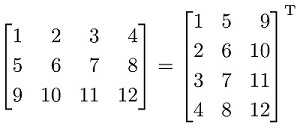
Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.
Особенности, определитель и свойства целочисленных
Свойства транспортирования целочисленных матриц:
- (A T ) T = A;
- (k · A) T = k · AT;
- (A + B) T = A T + В T ;
- (A · B) T = В T · A T
Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det A T = det A.
Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.
Формула, как обозначается транспонированная матрица
Если исходная матрица обозначается как А, то у транспортированной будет обозначение A T .
Тогда формула для транспортировки выглядит следующим образом:
A T ij = A ji
Формально, если А = m × n, то A T = n × m, но математически это записывается через индексы i и j.
Примеры задач на транспонирование матриц
Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.
Задача: даны А = (m × n) и В = (m × n).
Необходимо выполнить транспортирование.
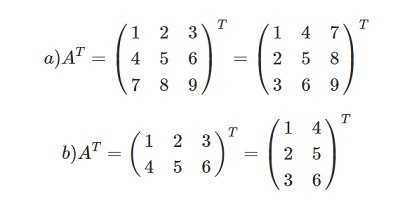
Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.
Функции для работы с матрицами в Excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
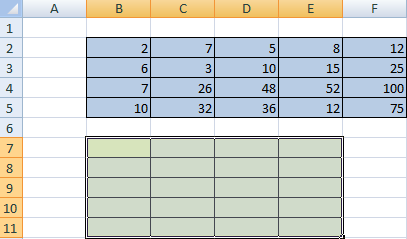
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
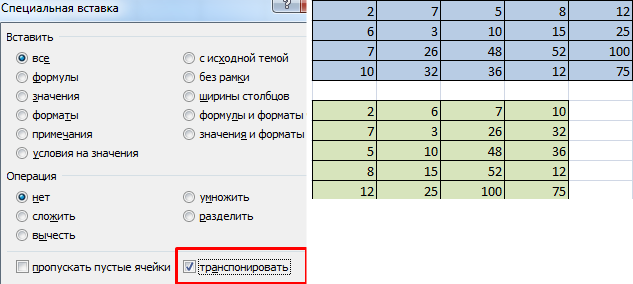
2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
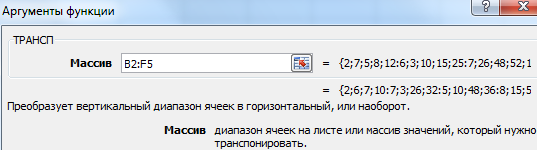
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
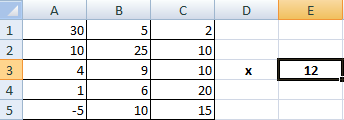
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
Для неособенной квадратной матрицы А обратной является матрица
, (2)
где —
определитель матрицы А, а
— матрица, союзная с матрицей А.
Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.
Пусть существует квадратная матрица A:
Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:
Остановимся на минорах и алгебраических дополнениях.
Пусть есть квадратная матрица третьего порядка:
.
Её определитель:
Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.
Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :
.
Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:
.
По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.
И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица
того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:
Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.
Пример 1. Для матрицы
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу
,
транспонированную относительно матрицы A:
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:
Следовательно, матрица
,
союзная с матрицей A, имеет вид
Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.
Транспонирование матрицы
Транспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.
➣ Численный пример
Для исходной матрицы:
Транспонированная будет выглядеть так:
➤ Пример на Python
Решим задачу транспонирования матрицы на Python. Создадим матрицу A:
>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> print(A)
]
Транспонируем матрицу с помощью метода transpose():
>>> A_t = A.transpose()
>>> print(A_t)
]
Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:
>>> print(A.T)
]
Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.
Свойство 1. Дважды транспонированная матрица равна исходной матрице:
➣ Численный пример
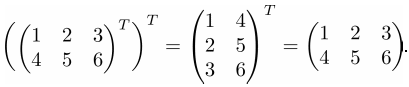
➤ Пример на Python
>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> print(A)
]
>>> R = (A.T).T
>>> print(R)
]
Свойство 2. Транспонирование суммы матриц равно сумме транспонированных матриц:
➣ Численный пример
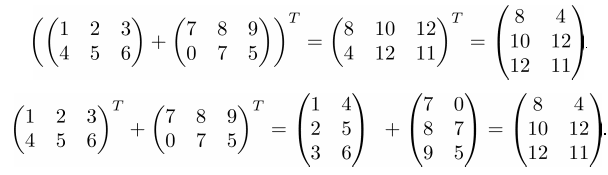
➤Пример на Python
>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> B = np.matrix(‘7 8 9; 0 7 5’)
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
]
>>> print(R)
]
Свойство 3. Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:
➣ Численный пример
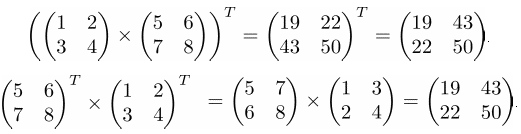
➤ Пример на Python
>>> A = np.matrix(‘1 2; 3 4’)
>>> B = np.matrix(‘5 6; 7 8’)
>>> L = (A.dot(B)).T
>>> R = (B.T).dot(A.T)
>>> print(L)
]
>>> print(R)
]
В данном примере, для умножения матриц, использовалась функция dot()из библиотеки Numpy.
Свойство 4. Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
➣ Численный пример
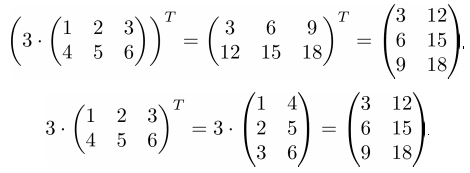
➤ Пример на Python
>>> A = np.matrix(‘1 2 3; 4 5 6’)
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
]
>>> print(R)
]
- Свойство 5. Определители исходной и транспонированной матрицы совпадают:
- ➣ Численный пример
- ➤ Пример на Python
>>> A = np.matrix(‘1 2; 3 4’)
>>> A_det = np.linalg.det(A)
>>> A_T_det = np.linalg.det(A.T)
>>> print(format(A_det, ‘.9g’))
-2
>>> print(format(A_T_det, ‘.9g’))
-2
Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.9g’).
P.S.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками.
Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Транспонирование матрицы
В данной публикации мы рассмотрим, как выполняется транспонирование матрицы, приведем практический пример для закрепления теоретического материала, а также перечислим свойства данной операции.
- Алгоритм транспонирования матрицы
- Свойства транспонирования матриц
Алгоритм транспонирования матрицы
Транспонированием матрицы называется такое действие над ней, когда ее строки и столбцы меняются местами.
Если исходная матрица имеет обозначение A , то транспонированную обычно обозначают как A T .
Пример Найдем матрицу A T , если исходная A выглядит так:
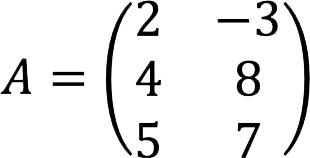
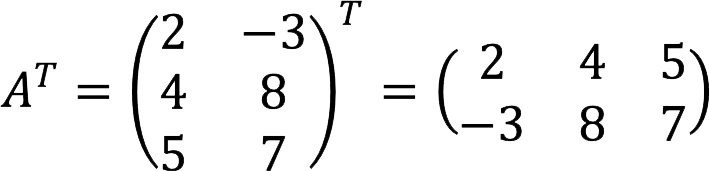
Свойства транспонирования матриц
1. Если матрицу транспонировать дважды, то в итоге получится она же.
2. Транспонировать сумму матриц – это то же самое, что и просуммировать транспонированные матрицы.
(A + B) T = A T + B T
3. Транспонировать произведение матриц – это то же самое, что и умножить транспонированные матрицы, но в обратном порядке.
4. Скаляр при транспонировании можно вынести.
5. Определитель транспонированной матрицы равняется определителю исходной. |A T | = |A|






























