Умножение матриц: примеры, алгоритм умножения на вектор, число, свойства произведения

Пишем микроядро (3-й шаг)

В предыдущей версии на 1 FMA операцию приходится 2 загрузки и 1 выгрузка.
Больше всего загрузок и выгрузок происходит с результирующей матрицей С: данные из нее нужно загрузить, прибавить к ним произведение C += A*B, и так много раз. Наиболее быстрая память, с которой может работать процессор — это его собственные регистры. Если мы будем хранить результирующее значение матрицы С в регистре процессора, то в процессе расчета нужно будет подгружать только значение матриц A и B. Теперь у нас на 1 FMA операцию приходится только 2 загрузки.
Если мы будем хранить в регистрах значения двух соседних столбцов матрицы C и C, то сможем повторно использовать загруженное значение матрицы A. И на 1 FMA операцию потребуется только 1.5 загрузки. Кроме того, сохраняя результат в 2 независимых регистра, мы позволим процессору выполнять 2 FMA операции за такт. Аналогично можно хранить в регистрах значения двух соседних строк — тогда будет осуществляться экономия на загрузке значений матрицы B.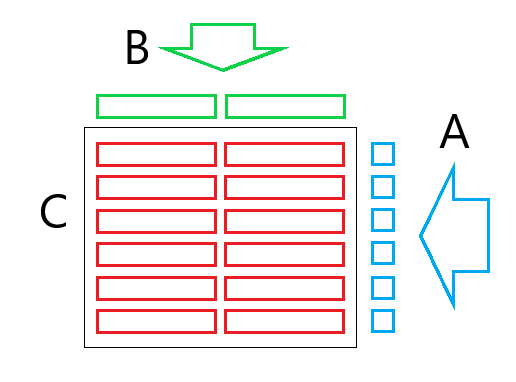
Всего настольные процессоры Интел начиная с 2-го поколения имеют 16 256-bit векторных регистров (справедливо для 64-bit режима процессора). 12 из них можно использовать для хранения кусочка результирующей матрицы С размером 6×16. В итоге мы сможем выполнить 12*8 = 96 FMA операций загрузив из памяти только 16 + 6 = 22 значений. И того нам удалось сократить доступ к памяти с 2.0 до 0.23 загрузки на 1 FMA операцию — почти в 10 раз! Функция которая осуществляет вычисление такого маленького кусочка матрицы С, обычно называется микроядром, ниже приведен пример такой функции:

Введем небольшую вспомогательную функцию для инициализации начального значения матрицы С:

Здесь lda, ldb, ldc — длина строчки (Leading Dimension в общем случае) соответсвующей матрицы.
Тогда функция умножения примет следующий вид:

Запускаем ее и получаем время исполнения 78.5 мс или 36.2 GFLOPS. Т.е. использование микроядра позволило ускорить матричное умножение почти в 3 раза. Но полученное быстродействие все еще далеко от максимального. Где теперь узкое место?

Алгебраические структуры

Кольцо квадратных плашек

Набор квадратных матриц фиксированного размера вместе с матричным сложением и матричным умножением образуют некоммутативное кольцо , кольцо матриц . Нулевой элемент этого кольца является нулевой матрицей . Если унитарное кольцо является унитарным кольцом , то ассоциированная матрица кольцо также одно целого с единичной матрицей в качестве одного элемента , где для всех матриц(Р.п×п,+,⋅){\ Displaystyle (R ^ {п \ раз п}, +, \ cdot)} ∈Р.п×п{\ Displaystyle 0 \ в R ^ {п \ раз п}}Р.{\ displaystyle R} Я.∈Р.п×п{\ Displaystyle I \ in R ^ {п \ раз п}}А.∈Р.п×п{\ Displaystyle А \ в R ^ {п \ раз п}}

А.⋅Я.знак равноЯ.⋅А.знак равноА.{\ displaystyle A \ times I = I \ times A = A}

применяется. В этом случае нулевая матрица действует как поглощающий элемент в кольце матриц , что означает, что следующее применимо ко всем матрицам :
А.∈Р.п×п{\ Displaystyle А \ в R ^ {п \ раз п}}

А.⋅знак равно⋅А.знак равно{\ Displaystyle А \ раз 0 = 0 \ раз А = 0}

Однако кольцо квадратных матриц не лишено делителей нуля ; from не обязательно следует за или . Соответственно, матричные уравнения сокращать нельзя, потому что это не обязательно следует . Набор квадратных матриц над полем образует ассоциативную алгебру с матричным сложением, скалярным умножением и матричным умножением .
А.⋅Б.знак равно{\ Displaystyle А \ cdot B = 0}А.знак равно{\ displaystyle A = 0}Б.знак равно{\ displaystyle B = 0}А.⋅Б.знак равноА.⋅С.{\ Displaystyle A \ cdot B = A \ cdot C}Б.знак равноС.{\ Displaystyle B = C}

Группа регулярных матриц

Множество регулярных матриц над унитарным кольцом образует общую линейную группу с матричным умножением . Матрица, обратная матрице , тогда явно выше
А.∈Р.п×п{\ Displaystyle А \ в R ^ {п \ раз п}}Р.{\ displaystyle R} GL⁡(п,Р.){\ Displaystyle \ OperatorName {GL} (п, R)}А.{\ displaystyle A}

А.⋅А.-1знак равноА.-1⋅А.знак равноЯ.{\ displaystyle A \ times A ^ {- 1} = A ^ {- 1} \ times A = I}

Определяются. Тогда для обратного к произведению двух регулярных матриц имеем:

(А.⋅Б.)-1знак равноБ.-1⋅А.-1{\ Displaystyle (A \ cdot B) ^ {- 1} = B ^ {- 1} \ cdot A ^ {- 1}}

Следовательно, в результате инверсии порядок умножения также меняется на обратный. Если регулярный, то применяется также правило редукции, т.е. от или затем следует .
А.{\ displaystyle A}А.⋅Б.знак равноА.⋅С.{\ Displaystyle A \ cdot B = A \ cdot C}Б.⋅А.знак равноС.⋅А.{\ Displaystyle В \ раз А = С \ раз А}Б.знак равноС.{\ Displaystyle B = C}

Группы ортогональных и унитарных матриц

Вещественная квадратная матрица называется ортогональной, если
А.∈Р.п×п{\ Displaystyle А \ в \ mathbb {R} ^ {п \ раз п}}

А.⋅А.Тзнак равноА.Т⋅А.знак равноЯ.{\ displaystyle A \ times A ^ {T} = A ^ {T} \ times A = I}

применяется. Ортогональные матрицы вместе с матричным умножением образуют ортогональную группу , подгруппу общей линейной группы . Соответственно, комплексная квадратная матрица называется унитарной, если
О⁡(п){\ displaystyle \ operatorname {O} (n)}GL⁡(п,Р.){\ Displaystyle \ OperatorName {GL} (п, \ mathbb {R})}А.∈С.п×п{\ Displaystyle А \ в \ mathbb {C} ^ {п \ раз п}}

А.⋅А.ЧАСзнак равноА.ЧАС⋅А.знак равноЯ.{\ displaystyle A \ times A ^ {H} = A ^ {H} \ times A = I}

применяется. При матричном умножении унитарные матрицы образуют унитарную группу , подгруппу общей линейной группы .
U⁡(п){\ Displaystyle \ OperatorName {U} (п)}GL⁡(п,С.){\ Displaystyle \ OperatorName {GL} (п, \ mathbb {C})}

Классы эквивалентности матриц

С помощью умножения матриц определяются отношения эквивалентности между матрицами над телом. Важными отношениями эквивалентности являются:

• Эквивалентность : две матрицы и называются эквивалентными, если есть две регулярные матрицы и такие, что выполняется.А.{\ displaystyle A}Б.{\ displaystyle B}С.{\ displaystyle C}Д.{\ displaystyle D}Б.знак равноС.-1⋅А.⋅Д.{\ Displaystyle B = C ^ {- 1} \ cdot A \ cdot D}
• Сходство : две квадратные матрицы и называются подобными, если существует такая регулярная матрица , что .А.{\ displaystyle A}Б.{\ displaystyle B}С.{\ displaystyle C}Б.знак равноС.-1⋅А.⋅С.{\ Displaystyle B = C ^ {- 1} \ cdot A \ cdot C}
• Конгруэнтность : две квадратные матрицы и называются конгруэнтными, если существует такая регулярная матрица , что .А.{\ displaystyle A}Б.{\ displaystyle B}С.{\ displaystyle C}Б.знак равноС.Т⋅А.⋅С.{\ Displaystyle B = C ^ {T} \ cdot A \ cdot C}

Таким образом, матрицы, которые могут быть преобразованы друг в друга посредством таких умножений на обычные матрицы, образуют классы эквивалентности .

Произведение матричных таблиц

Эта задача несколько сложнее предыдущих, но при этом в ней также нет ничего сложного.

Для осуществления умножения двух матриц $A \cdot B$ количество столбцов в $A$ должно совпадать с количеством строчек в $B$.

Математически это можно записать так:

$A_{m \times n}\cdot B_{n \times p} = С_{m \times p}$

То есть видя перемножаемые исходные матрицы можно сразу определить порядки получаемой новой. Например, если необходимо перемножить $A_{3 \times 2}$ и $B_{2 \times 3}$ — полученный результат будет иметь размер $3 \times 3$:

$\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \\ \end{pmatrix} \times \begin{pmatrix} b_{11} & b_{12} &b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} &b_{33} \\ \end{pmatrix} = \begin{pmatrix} • & • & • \\ • & • & • \\ • & • & • \\ \end{pmatrix}= \begin{pmatrix} (a_{11}b_{11} + a_{12}b_{21}) & (a_{11}b_{12} + a_{12}b_{22}) & (a_{11}b_{13} + a_{12}b_{23}) \\ (a_{21}b_{11} + a_{22}b_{21}) & (a_{21}b_{12} + a_{22}b_{22}) & (a_{11}b_{13} + a_{22}b_{23}) \\ (a_{31}b_{11} + a_{32}b_{21}) & (a_{31}b_{12} + a_{32}b_{22}) & (a_{31}b_{13} + a_{32}b_{23}) \\ \end{pmatrix}$

Если число столбцов первого матричного множителя не совпадает с количеством строчек второго матричного множителя, то умножение выполнить невозможно.

Пример 3

Решите пример:

$A \times B = ?$, если $A=\begin{pmatrix} 1 & 0 & 2 \\ -1 & 3 & 0 \\ 2 & 1 & 3 \\ \end{pmatrix}$ и $B = \begin{pmatrix} 3 & — 1 & 2 \\ -4 & 0 & 2 \\ 1 & 1 & 2 \\ \end{pmatrix}$.

$A \times B = \begin{pmatrix} (1 \cdot 3 + 0 \cdot (-4) + 2 \cdot 1) & (1 \cdot(-1) + 0 \cdot 0 + 2 \cdot 1) & (1 \cdot 2 + 0 \cdot 2 + 2 \cdot 2) \\ (-1) \cdot 3 + 3 \cdot (-4) + 0 \cdot 1) & (-1 \cdot(-1) + 3 \cdot 0 + 0 \cdot 1) & (-1 \cdot 2 + 3 \cdot 2 + 0 \cdot 2) \\ (2 \cdot 3 + 1 \cdot (-4) + 3 \cdot 1) & 2 \cdot (-1) + 1 \cdot 0 + 3 \cdot 1) & (2 \cdot 2 + 1 \cdot 2 + 3 \cdot 2) \\ \end{pmatrix} $

$A \times B= \begin{pmatrix} (3 + 0+ 2) & (-1 + 0 + 2) & (2 + 0 + 4) \\ (-3-12+0) & (1 + 0 + 0) & (-2+6+0) \\ (6-4+3) & (-2 + 0 + 3) & (4 + 2 + 6) \\ \end{pmatrix} = \begin{pmatrix} 5 & 1 & 6 \\ -15 & 1 & 4 \\ 5 & 1 & 12 \\ \end{pmatrix}$.

Переупорядочиваем матрицу B (4-й шаг)

Микроядро за каждую итерацию загружает два 256-bit вектора из матрицы B.
Причем каждый раз из новой строчки. Это делает невозможным для процессора эффективное кеширование этих данных. Для исправления этой ситуации сделаем два изменения:

1. Скопируем данные матрицы B во временный буфер таким образом, чтобы данные, необходимые одному микроядру лежали рядом.
2. Изменим порядок обхода матрицы С: сначала будем ходить по столбцам и только потом по строкам. Это позволит эффективнее использовать переупорядоченные значения матрицы B.

Для хранения буфера заведем небольшую структуру:

Здесь стоит отметить, что загрузка и выгрузка AVX векторов оптимально работает при выровненных данных, потому используются специальные функции для выделения памяти.
Функция переупорядочивания матрицы B:

Ну и собственно 4-я версия функции gemm:

Результаты тестирования (29.5 мс или 96.5 GFLOPS) показывают, что мы на правильном пути. Фактически достигнуто около 80% от теоретически возможного максимума.
Победа? К сожалению нет. Просто размер матриц, который мы использовали для тестирования (M=N=K=1152) оказался удобным для данной версии алгоритма. Если увеличить К в 100 раз (M=1152, N=1152, K=115200), то эффективность алгоритма упадет до 39.5 GFLOPS — почти в 2.5 раза.

Свойства произведения двух матриц

Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .              

Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.

Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы

на единичную матрицу справа и слева.

Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где

—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :

Получается, что АЕ = А .

Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :

Доказано: ЕА = А .

Проверить решение этой и других подобных задач можно на
калькуляторе произведения
матриц онлайн.

Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.

Свойство 3. Произведение матриц некоммутативно:.

Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.

Пример 11. Найти произведения матриц АВ и ВА, если

,

,

и убедиться в том, что эти произведения не равны друг другу:

.

Решение. Находим:

И действительно, найденные произведения не равны:.

Проверить решение этой и других подобных задач можно на
калькуляторе произведения
матриц онлайн.

Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .

Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .

Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то

.

Назад

Листать

Вперёд>>>

Поделиться с друзьями

Начало темы «Матрицы»

Продолжение темы «Матрицы»

Другие темы линейной алгебры

2.3. Определители

Каждой квадратной матрице по определённому правилу
можно поставить в соответствие единственное число.Это число называется определителем и
символически обозначается

.

Порядок определителя равен порядку квадратной матрицы.

Определитель
второго порядка вычисляется следующим образом

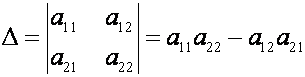,(2)

т.е.из произведения элементов, стоящих на так
называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний
угол), вычитается произведение элементов, находящихся напобочной диагонали (идущей из левого нижнего
в правый верхний угол).

П р и м е р. Вычислите определитель матрицы .

Р
е ш е н и е. Значения элементов
матрицы ,т.е.

Подставляем
в формулу (2) и получаем

.

Определитель
третьего порядка вычисляется с помощью формулы

(3)

З а м е ч а н и е.Чтобы легче
запомнить эту формулу, можно использовать так называемое правило треугольников
(правило Саррюса). Оно заключается в следующем. Элементы, произведения которых входят
в определитель со знаком «+», располагаются на главной диагонали и в вершинах
треугольников,симметричных относительно
главной диагонали

Элементы,
произведения которых входят в определитель со знаком «–», располагаются
аналогичным образом относительно побочной диагонали

П р и м е р. Вычислите определитель матрицы .

Р е ш е н и е. Подставляем значения элементов матрицы в формулу (3) и находим
величину заданного определителя

Для вычисления определителей третьего
порядка можно пользоваться ещёправилом «35». Согласно этому правилу к заданной матрице

добавляют
ещё первые два столбца

.

Элементы, произведения которых входят в определитель
со знаком «+», располагаются на главной диагонали и на отрезках, параллельных
главной диагонали

.

Элементы, произведения которых входят в определитель
со знаком «–», располагаются на побочной диагонали и на отрезках, параллельных
побочной диагонали

.

Определитель
равен сумме указанных
произведений элементовс учетом их
знаков.

Основные
свойства определителей

Рассмотрим основные свойства определителей 2-го и 3-го
порядка

С в о й с т в о1. Определитель не
изменяется при транспонировании, т.е.

.(4)

Действительно,

,

=,

Из чего следует
справедливость равенства (4).

Из свойства 1
следует, чтосвойствами определителей,
сформулированные для строк будут такими же как и для столбцов. Поэтомуследующие свойства определителей будут формулироваться
только для строк.

С в о й с т в о 2. При умножении элементов строки определителя на
некоторое числоопределитель умножается
на это число, т.е.

В справедливости этого свойства можно убедиться,
вычислив эти определители

Свойство 3.
Определительравен нулю в следующих
случаях:

a)одна из строк
нулевая

,

б) две равные строки

в)элементы
двух строкпропорциональны

В
справедливости перечисленных свойств легко убедиться с помощью формулы (3).

С в о й с т в о 4. Если две какие-либо строки определителя поменять
местами, то знак определителя изменится на противоположный

Доказательство
этого свойства выполняется с помощью формулы (3).

С в о й с т в о5. Еслив
определителе некоторая строка, например, первая является линейной
комбинациейдвух строк с коэффициентами и

,

то определитель будет
равен сумме двух определителей, определяемых формулой

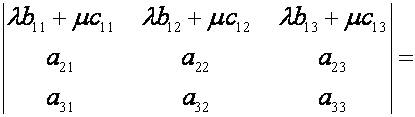
Справедливость
этого свойства можно доказать, сравнив значения левой и правой частей
равенства, найденные с помощью формулы (3).

С в о й с т в о6. Величина определителя
не изменится, если к элементам одной строки прибавить соответствующие элементы
другой строки, умноженные на одно и то же число

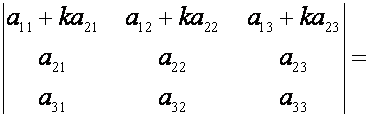
Основные свойства матричного произведения

В двух словах. Умножение матриц:

1. Некоммутативно: $A\cdot B\ne B\cdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $A\cdot B=B\cdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
2. Ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
3. Дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$ и $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.

А теперь — всё то же самое, но более подробно.

Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.

Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:

\\cdot \left=\left\]

Но если поменять матрицы местами, то получим совсем другой результат:

\\cdot \left=\left\]

Получается, что $A\cdot B\ne B\cdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=\left$ и $B=\left$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $\left$ и $\left$ вполне себе согласованы в указанном порядке, но те же матрицы $\left$ и $\left$, записанные в обратном порядке, уже не согласованы. Печаль.:(

Тем не менее, умножение матриц ассоциативно:

\

Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.

В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $\left$. Множество всех таких матриц обозначается ${{M}^{n}}$ (т.е. записи $A=\left$ и \ означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.

Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:

\

Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)

Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.

Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?

Ассоциативность

Т

Теорема 2. Операция умножения матриц подчиняется ассоциативному закону:
$$ (A\cdot B) \cdot D = A\cdot (B \cdot D) $$
если хотя бы в одной части равенства произведение определено.

Доказательство. Пусть $ A \in \mathbb A^{m \times n}, B \in \mathbb A^{n \times k}, D \in \mathbb A^{k \times h} $. Пусть
$$
A=
\left( \begin{array}{lllll}
a_{11} & a_{12} & a_{13}& \dots & a_{1n} \\
a_{21} & a_{22} & a_{23}& \dots & a_{2n} \\
\dots & & & & \dots \\
a_{m1} & a_{m2} & a_{m3}& \dots & a_{mn}
\end{array}
\right) \ , \quad
B=
\left(\begin{array}{llll}
b_{11} & b_{12} & \dots & b_{1k} \\
b_{21} & b_{22} & \dots & b_{2k} \\
\dots & & & \dots \\
b_{m1} & b_{m2} & \dots & b_{mk}
\end{array}\right) \, .
$$
Докажем сначала справедливость равенства для частного случая матрицы $ D $: пусть она состоит только из одного столбца, т.е. $ h=1 $. Обозначим этот столбец
$$
X=
\left(\begin{array}{l}
x_1 \\ x_2 \\ \vdots \\ x_n
\end{array}\right)
$$
Сделаем в векторе
$$
AX=\left(
\begin{array}{c}
a_{11}x_1 +a_{12}x_2+ \ldots+a_{1n}x_n \\
a_{21}x_1 +a_{22}x_2+ \ldots +a_{2n}x_n \\
\dots \\
a_{m1}x_1 +a_{m2}x_2+ \ldots+a_{mn}x_n
\end{array}
\right)
$$
замену переменных (подстановку) по формулам
$$
X=BY \quad \iff \quad
\left\{\begin{array}{l}
x_1=b_{11}y_1+b_{12}y_2+\dots+b_{1k}y_k\ ,\\
\vdots\\
x_n=b_{n1}y_1+b_{n2}y_2+\dots+b_{nk}y_k\ .
\end{array}\right.
$$
Здесь
$$
Y=
\left(\begin{array}{l}
y_1 \\ y_2 \\ \vdots \\ y_k
\end{array}\right)
$$
— вектор новых переменных.

Подстановка в $ a_{j1}x_1+a_{j2}x_2+\dots+a_{jn}x_n $ приводит к следующему:
$$\begin{array}{rlc}
a_{j1}x_1+a_{j2}x_2+\dots+a_{jn}x_n=
&a_{j1}(b_{11}y_1+b_{12}y_2+\dots+b_{1k}y_k)&+\\
+&a_{j2}(b_{21}y_1+b_{22}y_2+\dots+b_{2k}y_k)&+\\
+& \qquad \qquad \dots & +\\
+&a_{jn}(b_{n1}y_1+b_{n2}y_2+\dots+b_{nk}y_k)&=\\
=&(a_{j1}b_{11}+a_{j2}b_{21}+\dots+a_{jn}b_{n1})y_1&+\\
+&(a_{j1}b_{12}+a_{j2}b_{22}+\dots+a_{jn}b_{n2})y_2&+\\
+& \qquad \qquad \dots&+\\
+&(a_{j1}b_{1k}+a_{j2}b_{2k}+\dots+a_{jn}b_{nk})y_k&=\\
=c_{j1}y_1+c_{j2}y_2+\dots+c_{jk}y_k ,& &
\end{array}
$$
где коэффициенты определяются формулой
$$ c_{j\ell}=a_{j1}b_{1\ell}+a_{j2}b_{2\ell}+\dots+a_{jn}b_{n\ell} \, . $$
Однако, этой же формулой определяются элементы матрицы
$$ C = A \cdot B \, . $$
Таким образом, справедливость равенства
$$
A(BY)=(AB)Y
$$
доказана для любого столбца $ Y \in \mathbb A^{k\times 1} $.

Распространить же его на матрицу $ D $ с произвольным количеством столбцов позволяет теорема $1$. Умножение матрицы $ C $ на матрицу $ D $ сводится к умножению матрицы $ C $ на каждый из столбцов
матрицы $ D $:
$$C\cdot } \mid \dots \mid D_{} ] =\left} \mid \dots \mid C \cdot D_{} \right] = $$
На основании уже доказанной формулы имеем право записать
$$(AB)D_{}=A\left(BD_{}\right),\dots,
(AB)D_{}=A\left(BD_{}\right) \ .
$$
Следовательно, наше произведение
$$
=
\left} \right) \mid \dots \mid A\left(BD_{} \right) \right] =
$$
Снова используем правило умножения матрицы на матрицу по теореме $ 1 $ (только теперь идем в обратном направлении — от столбцов переходим к матрице):
$$
=A \left} \mid \dots \mid BD_{} \right] =
$$
и завершит доказательство еще одно применение того же правила:
$$
=A(BD) \ .
$$

Умножение матриц Excel – voxt.

Объяснение

Умножение матриц — одна из полезных функций Excel, предназначенных для выполнения математических операций. Это помогает получить произведение двух матриц. Матрицы, которые нужно умножить, имеют определенное количество строк и столбцов для представления данных. Размер полученной матрицы берется из количества строк первого массива и количества столбцов второго массива. Есть условие умножения матриц; количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.

Для выполнения матричного умножения используется предопределенная функция MMULT, представленная в программном обеспечении Excel.

В общем, умножение матриц выполняется двумя способами. Простое скалярное умножение выполняется с использованием основных арифметических операций, а расширенное умножение матриц управляется с помощью функции массива в Excel.

Формула Excel, используемая для умножения, вводится двумя способами, включая ручной ввод функции MMULT после знака равенства или выбор библиотеки функций Math and Trig, представленной на вкладке «Формулы». Математическая функция MMULT помогает вернуть результат умножения двух массивов. Это одна из предопределенных функций Excel, используемых в рабочих таблицах для выполнения расчетов за короткое время.

Синтаксис

• Параметры: Array1 и Array2 — два параметра, необходимые для умножения.
• Правило: Столбцы массива array1 должны быть равны строкам array2, а размер продукта равен количеству строк в array1 и количеству столбцов в array2.
• Возврат: Функция MMULT генерирует числа в матрице продукта. Он вводится как формула или функция рабочего листа в вычислениях Excel.

Рассматривать,

Тогда произведение A * B выглядит следующим образом.

Как сделать умножение матриц в Excel? (с примерами)

Умножение матриц в Excel имеет некоторое приложение в реальном времени. Есть два способа выполнить матричное умножение. Ниже приведены несколько примеров умножения матриц Excel.

Вы можете скачать этот шаблон Excel для умножения матриц здесь — Шаблон для умножения матриц в Excel

Пример №1 — Умножение матрицы на скалярное число.

Шаг 1: В первую очередь необходимо ввести данные в массив.

Шаг 2: Выберите скалярное значение, которое мы собираемся умножить на массив, т.е. 3

• Шаг 3: Оцените строки и столбцы результирующего массива.
  Здесь результирующий массив будет размером 3 x 3.
• Шаг 4: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат, и введите обычную формулу умножения.

Шаг 5: После ввода формулы нажмите Ctrl + Shift + Enter. И результат будет, как показано на нижеприведенном рисунке.

Пример # 2 — Матричное умножение двух отдельных массивов

Шаг 1: В первую очередь необходимо ввести данные в массив А размером 3 × 3.

Шаг 2: Введите данные во второй массив под названием B размером 3 × 3.

• Шаг 3: Нам нужно убедиться, что столбцы первого массива имеют такой же размер, как и строки второго массива.

Шаг 4: Оцените строки и столбцы результирующего массива.

Шаг 5: Выберите диапазон ячеек, равный размеру результирующего массива, чтобы разместить результат, и введите формулу умножения MMULT.

Введите значения, чтобы вычислить произведение A и B.

После ввода формулы нажмите Ctrl + Shift + Enter чтобы получить результат. Результаты получаются путем умножения двух массивов следующим образом, а размер результирующего массива составляет 3×3.

Пример # 3

Умножение матриц между массивами с одной строкой и одним столбцом. Рассмотрим элементы матриц как

Матрица A имеет размер 1 × 3, а матрица B — 3 × 1. Размер изделия А * Б матрица 1 × 1. Итак, введите в ячейку формулу умножения матриц.

Нажмите Enter, чтобы получить результат.

Матрица A имеет размер 3 × 1, а матрица B — 1 × 3. Размер изделия А * Б матрица 3 × 3.

Итак, ответ будет такой:

Пример # 5 — Определение квадрата матрицы с помощью MMULT в Excel

Квадрат матрицы A определяется умножением A на A.

Результирующая матрица получается как

Чтобы выполнить матричное умножение, количество столбцов, представленных в массиве 1, и количество строк, представленных в массиве 2, равны.
Изменить часть массива сложно, так как массив представляет собой группу элементов.
При выполнении умножения массива следует использовать CTRL + SHIFT + ENTER для создания всех элементов результирующей матрицы. В противном случае производится только один элемент.
Элементы массива не должны быть нулевыми, а текст не должен использоваться в матрицах, чтобы избежать ошибок.
Размер массива товаров равен строкам первого массива и столбцам второго массива.
Умножение A * B не равно умножению B * A в матричном умножении.

Умножение матрицы на единичную матрицу приводит к той же матрице (т.е. *знак равно)

Post Views: 848

Как найти произведение двух матриц 3х3

Для того чтобы умножить две матрицы размера 3х3, необходимо выполнить определенную последовательность действий. Сначала необходимо найти произведения элементов первой строки первой матрицы на соответствующие элементы первого столбца второй матрицы. Затем найденные произведения необходимо сложить и записать в первую ячейку итоговой матрицы. Аналогичным образом вычисляются остальные элементы итоговой матрицы.

Для удобства вычислений можно представлять каждую матрицу в виде таблицы размера 3х3. Элементы матриц обозначаются как a_ij, где i — номер строки, а j — номер столбца. Например, a₁₂ обозначает элемент, расположенный на пересечении 1 строки и 2 столбца.

a11	a12	a13
a21	a22	a23
a31	a32	a33

Таким образом, произведение матриц a и b вычисляется следующим образом:

a11	a12	a13
a21	a22	a23
a31	a32	a33

Например, чтобы найти элемент c₁₂ итоговой матрицы c, необходимо выполнить следующие вычисления:

c₁₂ = a₁₁ * b₁₂ + a₁₂ * b₂₂ + a₁₃ * b₃₂

Выполнив аналогичные вычисления для всех элементов матрицы c, получим искомый результат.

использовать

Факторинг

В некотором смысле, обратная матрицы умножения факторинг данной матрицы в виде произведения двух матриц и , то есть найти представление формы
А.{\ displaystyle A}Б.{\ displaystyle B}С.{\ displaystyle C}

А.знак равноБ.⋅С.{\ Displaystyle А = В \ cdot C}.

Такая факторизация не уникальна, как и к матрицам и к ним предъявляются дополнительные требования, такие как ортогональность , симметрия или конкретная структура занятости. Важными разложениями вещественных или комплексных матриц этого типа являются:
Б.{\ displaystyle B}С.{\ displaystyle C}

• LR разложение квадратной матрицы в нижнюю и верхнюю треугольную матрицу
• разложение Холецкого , специальное разложение LR из симметрично положительно определенной матрицы
• разложение ILU , вид неполного разложения LU специально для разреженных матриц
• QR — разложение матрицы в ортогональную матрицу и верхняя треугольная матрица
• разложение Шура квадратной матрицы в трех матриц: унитарная матрица, верхняя треугольная матрица и обратная первой матрицы
• сингулярное разложение матрицы на три матриц: а унитарная матрица , диагональная матрица , состоящая из сингулярных значений и сопряженная унитарной матрицы

Такое разложение матриц часто используется в численной линейной алгебре для решения линейных систем уравнений или задач на собственные значения . Например, преобразования строк и столбцов в методе исключения Гаусса могут быть указаны как произведение элементарных матриц.

Выполнение двух линейных отображений друг за другом как умножение матриц

Линейные карты

Если общее и два конечномерных векторных пространства находятся над одним и тем же телом, то каждое линейное отображение может быть представлено своей матрицей отображения , в зависимости от выбора базы в каждом из двух векторных пространств . Изображение вектора ниже на рисунке в соответствующих базах затем могут быть использованы с помощью матрично-векторного произведения
В.{\ displaystyle V}W.{\ displaystyle W} жВ.→W.{\ displaystyle f \ двоеточие с V \ на W} М.ж{\ displaystyle M_ {f}} y{\ displaystyle y}Икс{\ displaystyle x}ж{\ displaystyle f}

yзнак равноМ.ж⋅Икс{\ displaystyle y = M_ {f} \ cdot x}

определяется. В геометрии , например, каждое вращение вокруг начала координат и каждое отражение в исходной плоскости могут выполняться таким образом с помощью такого произведения матрица-вектор. Если теперь есть дополнительное векторное пространство и дополнительное линейное отображение, то следующее применяется к матрице отображения последовательного выполнения этих двух отображений:
U{\ displaystyle U}граммW.→U{\ displaystyle g \ двоеточие W \ to U} грамм∘ж{\ displaystyle g \ circ f}

М.грамм∘жзнак равноМ.грамм⋅М.ж{\ displaystyle M_ {g \ circ f} = M_ {g} \ cdot M_ {f}}

Матрица отображения последовательного выполнения двух линейных отображений, следовательно, является матричным произведением двух связанных матриц отображения. Таким образом, например, каждое поворотное зеркальное отображение может быть представлено как произведение поворотной матрицы и зеркальной матрицы. В качестве альтернативы, линейное отображение также может быть выполнено путем векторно-матричного умножения линейного вектора на транспонированную матрицу отображения. Последовательное выполнение отображений тогда соответствует умножению матриц справа, а не слева.

Приложения

Приложения матричного умножения можно найти среди прочего:

• в анализе при составлении дифференцируемых функций нескольких переменных по правилу многомерной цепочки
• в компьютерной графике при выполнении преобразований координат в графическом конвейере
• в оптике при расчете световых лучей через оптические компоненты с использованием матричной оптики
• в экономике в вводе-выводе анализе в производстве , а также во внутренней сопряженности из материалов
• в робототехнике при описании кинематических цепей с помощью преобразования Денавита-Хартенберга
• в электротехнике в двухпортовой теории электрических сетей
• в квантовой механике в рамках матричной механики , здесь также для «бесконечно больших» матриц

См. Также :