Обыкновенные дроби — определение и вычисление с примерами решения

Вычитание дробей с разными знаменателями

Если знаменатели разные, то нужно сделать так, чтобы они стали одинаковыми, т.е. привести дроби к общему знаменателю. После этого совершаем те же действия, что и выше.

Примеры

Пример 3:

Найдите разность 5/10 – 2/5.

Решение:

5/10 – 2/5 = 5/10 – 2•2/2•5 = 5/10 – 4/10 = 5-4/10 = 1/10 = 0.1

Чтобы найти общий знаменатель, нужно числитель и знаменатель второй дроби умножить на 2. Получим 4/10. Теперь можно находить разность как в прошлом примере.

Перейдем к следующему примеру.

Пример 4:

Найдите разность 52/24 – 14/12.

Решение:

52/24 – 14/12 = 52/24 – 2•14/2•12 = 52/24 – 28/24 = 52-28/24 = 24/24 = 1

Для того, чтобы привести к общему знаменателю, нужно умножить числитель и знаменатель второй дроби на 2. Будь в двух знаменателях 7 и 49, то мы бы умножали 7 не на 2, а на 7, чтобы получить в обоих знаменателях 49. Дальше все по формуле.

Вычитание натурального числа из обыкновенной дроби

Для того чтобы вычесть натуральное число из обыкновенной дроби, нужно представить натуральное число в виде обыкновенной дроби.

Рассмотрим на примере.

Примеры

Пример 5:

Найдите разность 288/36 – 6.

Решение:

288/36 – 6 = 288/36 – 6/1 = 288/36 – 36•6/36•1 = 288/36 – 216/36 = 288-216/36 = 72/36 = 2

Может показаться, что это сложно, но это не так. Число 6 можно представить в виде обыкновенной дроби: 6/1. Далее будем находить разность этих дробей. Приводим дроби к общему знаменателю, умножая знаменатель и числитель второй дроби на 36. Вычитаем, делим и получаем ответ.

Есть и второй вариант решения (для неправильных дробей, где числитель больше знаменателя) такого примера, более удобный и простой. Возьмем новые числа.

Пример 6:

Найдите разность 72/27 – 2.

Решение:

72/27 – 2 = 2 2/3 – 2 = 2/3

В этом случае не пришлось превращать натуральное число в дробь, 72/27 мы сделали смешанным числом, отняли двойки и получили ответ. Можно решать на основе прошлого примера, однако, это будет дольше и сложнее.

Понятия

• Смешанное число – это такая правильная дробь, в состав которой входит целое число.
• Неправильная дробь – это дробь, в которой числитель равен знаменателю или больше его.
• Правильная дробь – это дробь, в которой знаменатель больше числителя.

Для того, чтобы преобразовать неправильную дробь в смешанное число, необходимо поделить ее числитель на знаменатель. Неполное частное станет целой частью смешанной дроби, остаток будет числителем дробной части, а знаменатель неправильной дроби – знаменателем дробной части.

1.2.1. document.write(‘Обыкновенные дроби’); window.top.document.title = «1.2.1. Обыкновенные дроби»;

Можно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби.

	Обыкновенной дробью называется число вида где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.

Если n = 1, то дробь имеет вид
и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.

	Две дроби и называются равными, если

Например,
так как
Из этого определения следует, что дробь
равна любой дроби вида
где m – натуральное число. В самом деле, так как
то   Итак, мы готовы сформулировать следующее правило.

Основное свойство дроби Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной.

С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например,
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например,
– несократимая дробь.

Модель 1.5. Сокращение обыкновенных дробей

	Обыкновенная дробь называется правильной, если её числитель меньше её знаменателя, то есть m < n. Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n.

Справедливо следующее утверждение (его мы докажем ниже):

Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.

Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например,
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.

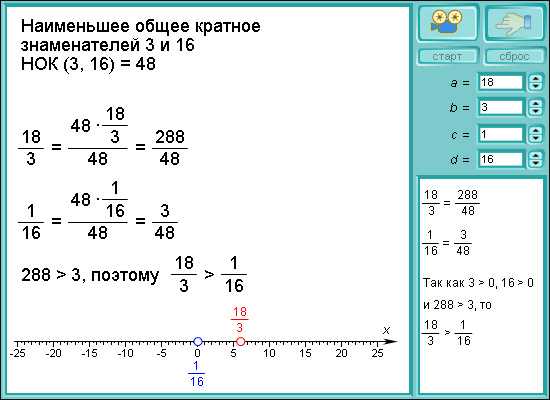Модель 1.6. Сравнение обыкновенных дробей

Теперь знаменатели этих дробей одинаковы, значит,
Следовательно,
Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби  и 
можно привести к знаменателю 56. В самом деле:

наименьшему общему знаменателю
Пример 1

Привести дроби к наименьшему общему знаменателю:  и 

Решение

Найдём сперва наименьшее общее кратное чисел 15 и 20. НОК (15, 20) = 60. Так как 60 : 15 = 4, то числитель и знаменатель дроби нужно умножить на 4: Поскольку 60 : 20 = 3, то числитель и знаменатель второй дроби нужно умножить на 3: Итак, дроби приведены к общему знаменателю: Ответ.

В рассмотренном примере числа 4 и 3 называют дополнительными множителями для первой и второй дроби соответственно.

Теперь мы можем определить арифметические действия с дробями.

Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть

Вычитание. Если две дроби имеют одинаковые знаменатели, то

Модель 1.7. Сложение и вычитание обыкновенных дробей

Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть

Деление. Деление дробей осуществляют следующим образом:

В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.

Модель 1.8. Умножение и деление обыкновенных дробей

Пример 2

Сложить две дроби
и
Ответ представить в виде неправильной дроби.

Показать решение

Пример 3

Сложить две дроби
и
Ответ представить в виде неправильной дроби.

Показать решение

Теперь можно показать, что любую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь
такова, что число m кратно n, например, ).

Пример 4

Представить неправильную дробь в виде суммы натурального числа и правильной дроби: 1)
2)

Показать решение

Всякую неправильную дробь можно представить в виде смешанного числа (или в виде натурального числа). Понятно также, что верно и обратное: всякое смешанное число может быть представлено в виде неправильной дроби. Например,

Пример 5

Выполнить действия.

Показать решение

Куб дроби. Дробь в третьей степени.

• Альфашкола
• Статьи
• Куб дроби

Какие действия необходимо сделать, чтобы выполнить возведение в куб дроби? Для этого стоит определить какая дробь смешанная или обыкновенная, десятичная или недясятичная.

Для того чтобы  возвести обыкновенную дробь в куб надо числитель  и знаменатель возвести в степень. Пример :

Для того чтобы возвести смешанную дробь в куб надо ее перевести в неправильную дробь, а затем числитель и знаменатель возвести в степень и в полученной дроби выделить целую часть.

При возведении в третью степень десятичного числа надо вычислить произведение трех ее множителей, равных самой дроби. Пример:

Дробь:           ————

———-

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Камо Аркадьевич Филипосян

Репетитор по математике

Стаж (лет)

Образование:

Самаркандский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике для 8-11 классов и по физике для 7-9 классов.

Елена Вячеславовна Гришаева

Репетитор по математике

Стаж (лет)

Образование:

Рязанский государственный педагогический университет имени С. А. Есенина

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор для 5-10 классов.

Аурика Витальевна Чуева

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по русскому языку и по математике для 1-4 классов, подготовка к школе. Помогу в выполнении домашнего задания. Использую индивидуальный подход к каждому ребенку, легко нахожу общий язык, стараюсь достигать поставленных целей.

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Действительные числа

Какие же это числа? Мы ещё не рассмотрели операцию возведения в степень. Например, 42=4 ·4 = 16. 53=5 ·5 ·5=125. Как умножение представляет собой более удобную форму записи и вычисления сложения, так и возведение в степень – это форма записи умножения одного и того же числа самого на себя определенное количество раз.

Но теперь рассмотрим операцию, обратную возведению в степень – извлечение корня. Квадратный корень из 16 – это число, которое в квадрате даст 16, то есть число 4. Квадратный корень из 9 – это 3. А вот квадратный корень из 5 или из 2, например, не может быть представлен рациональным числом. (Доказательство этого утверждения, другие примеры иррациональных чисел и их историю можно посмотреть, например, в Википедии)

В ГИА в 9 классе есть задание на определение того, является ли число, содержащее в своей записи корень, рациональным или иррациональным. Задача заключается в том, чтобы попытаться преобразовать это число к виду, не содержащему корень (используя свойства корней). Если от корня не удается избавиться, то число иррациональное.

Другим примером иррационального числа является число π, знакомое всем из геометрии и тригонометрии.

Определение: Рациональные и иррациональные числа вместе называют действительными (или вещественными) числами. Множество всех действительных чисел обозначают буквой R.

В действительных числах, в отличии от рациональных, мы можем выразить расстояние между любыми двумя точками на прямой или на плоскости.
Если нарисовать прямую и выбрать на ней две произвольные точки или выбрать две произвольные точки на плоскости, то может так получиться, что точное расстояние между этими точками невозможно выразить рациональным числом. (Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1 по теореме Пифагора будет равна корню из двух – то есть иррациональному числу. Сюда же относится точная длина диагонали тетрадной клетки (длина диагонали любого идеального квадрата с целыми сторонами).)
А в множестве действительных чисел любые расстояния на прямой, в плоскости или в пространстве могут быть выражены соответствующим действительным числом.

Минутка истории

Точное время появления дробных выражений пока не установлено. Но исторические находки предполагают, что они возникли в связи с жизненной необходимостью. Задания с использованием дробей считались самыми сложными, и выполнять их могли, только люди, обладающие огромным умственным потенциалом. За такие знания, мудрецов почитали на уровне бога. Ведь без их помощи невозможно было разделить добычу между всеми охотниками поровну, уловмежду рыбаками, урожай между соседями. До сих пор в Германии существует поговорка «Оказаться в дробях», – это значит попасть в попасть в непонятную, запутанную ситуацию.

На Русь, понятие «дробь»пришлов начале 9 века. Источником этого понятия стало выражение «дробить» (разделять, разламывать). На протяжении длительного времени,разные народы называли такие числа ломаными, ведь при разделении любого предмета (конфета, яблоко, хлеб) его приходилось разламывать.

В России существовала отдельная единица измерения для определения размеров земельных наделов, она состояла из четверти и получетверти. Еще эту единицу называли осьмина. Это была дробь, которая использовалась только для измерения земельных угодий. Осьминой невозможно измерить другие величины, скорость или количество прибыли. Гораздо позже эта единица измерения преобразовалась в 1/8, которую можно применять для измерения любой величины.

В произношении дробных чисел на Руси, были свои правила. В название, дробного числа,знаменатель которого больше 5, и меньше 11 добавлялось окончание «ина»: 1/6– шестина, 1/9– девятина, 1/10– десятина. Если дробь имела в знаменателе число больше 10, то в названии дроби обязательно произносились слово «жеребей»: 4/13 – четыре тринадцатых жеребьев.

Число, которое записывалось над чертой, называли верхнее число, а число под чертой – исподнее число.

Где в жизни мы можем встретить дроби:

— При использовании мер измерения: 1 грамм=1/1000 килограмма=1/100000 центнера

— Охотники,используют дробь.

— В медицине. Каждое лекарственное средство, в своем составе, содержит различные компоненты, измеряющиеся дробями.

— Быструю, резкую игру на барабанах называют барабанной дробью.

— По команде капитана корабля «дробь» сразу прекращается огонь.

— При нумерации домов использование дробей уместно на двух пересекающихся улицах.

— Основными движениями в русских народных танцах является дробь и бег.

— Во всех кулинарных рецептах, необходимые пропорции указаны дробными числами: 2/3 стакана муки или 3/4 яблока.

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Вычисление дроби от числа

До сих пор мы с вами находили доли (дроби) от одного. Но как быть, если нам нужно найти часть не от $1$, а от какого-то другого числа?

Например, мы знаем, что в минуте $60$ секунд. Сколько будет секунд в $\frac{1}{3}$ минуты?

Показать ответ

Скрыть

Найдем треть от $60$:$\newline$ $60:3=20$ секунд.

{"questions":[{"content":"В двух клетках сидят $2$ белых и $3$ черных кролика. Между кроликами нужно поровну разделить $10$ морковок.`image-1`Сколько морковок необходимо положить к черным кроликам?`choice-14`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/08/kroliki.svg"},"choice-14":{"type":"choice","options":,"explanations":,"answer":}},"step":1,"hints":}]}

Числитель и знаменатель

Обыкновенная дробь состоит из числителя и знаменателя.

Определение 3

Числителем обыкновенной дроби $\frac{m}{n}$ называется натуральное число $m$, которое показывает количество взятых равных долей из единого целого.

Определение 4

Знаменателем обыкновенной дроби $\frac{m}{n}$ называется натуральное число $n$, которое показывает, на сколько равных долей разделено единое целое.

Рисунок 1.

Числитель располагается над дробной чертой, а знаменатель —под дробной чертой. Например, числителем обыкновенной дроби $\frac{5}{17}$ является число $5$, а знаменателем — число $17$. Знаменатель показывает, что предмет разделен на $17$ долей, а числитель — что взято $5$ таких долей.

Базовая математика — Типы дробей

Поиск на моем сайте:

Поделись этой страницей!

Я помогу вам объяснить вашему ребенку дроби.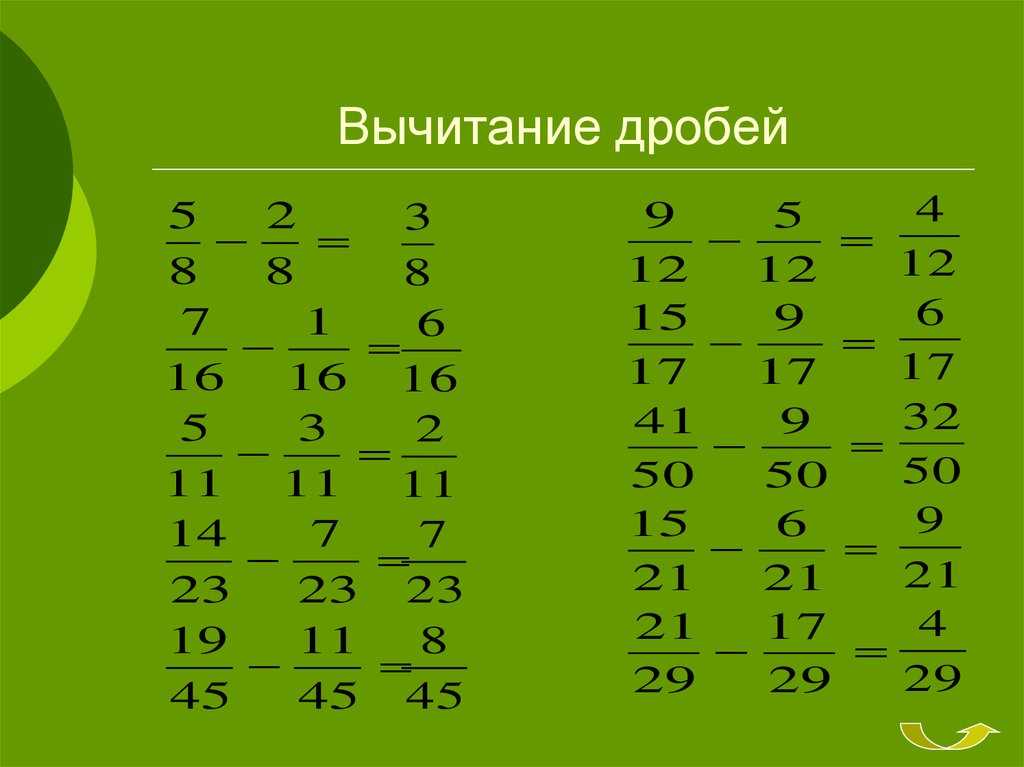

Когда дело доходит до чисел, целые числа — это числа, которые мы знаем: 1, 2, 3 и так далее. Дроби — это числа, которые записываются из 2 частей: числителя и знаменателя.

Смешанные дроби или смешанные числа

Когда мы объединяем целые числа и дроби, мы получаем смешанную дробь, также называемую смешанным числом.

Следовательно, смешанное число состоит из целого числа и дроби.

Правильные дроби и неправильные дроби

Правильная дробь – это дробь, у которой числитель меньше знаменателя. Это то, о чем мы обычно думаем как о дроби.

Помните, что числитель говорит нам, сколько частей мы хотим, в то время как знаменатель говорит нам общее количество частей, на которые делится целое число.

Целые числа также можно записывать в виде дроби. Например, 4/4 означает 4 из 4, что равно 1 целому.

Неправильная дробь – это та, у которой числитель больше знаменателя. Это происходит, когда мы включаем в дробь целое число из смешанной дроби.

См. примеры ниже.

Простой способ запомнить, как преобразовать целое число в неправильную дробь, — это умножить целое число на знаменатель.

Добавление дробей

Эквивалентные дроби

Эквивалентные дроби говорят нам об одинаковом размере.

Дроби включают в себя деление целого на более мелкие части или разбиение большой группы на более мелкие группы, поэтому мы можем получить одинаковый размер, даже если мы разделим по-разному.

Пример У меня есть шоколадный торт и обычный торт одинакового размера. Шоколадный корж я разрезаю на 4 равные части, а обычный корж разрезаю на 2 равные части.

Поскольку шоколадный торт разрезается на 4 части, 2 части составляют 2/4 (две четверти) всего торта.

Аналогично, один кусок простого торта представляет собой 1/2 (половину) всего торта. Это означает, что 2/4 и 1/2 имеют одинаковый размер, поэтому мы говорим, что 2/4 эквивалентно 1/2.

Вот еще один способ посмотреть на эквивалентные дроби:

Я разрезал торт на 2 равные части.

Затем я разрезал каждую из частей на 2 меньшие равные части. Сейчас у меня 4 маленьких кусочка. 2 из этих маленьких кусочков будут того же размера, что и один из предыдущих кусочков.

Это
означает, что для того, чтобы найти эквивалентные дроби, мы должны умножить обе
числитель (верхнее число) и знаменатель (нижнее число) на одно и то же число.

Таким образом, понятие эквивалентности аналогично понятию равенства.

Эквивалентные дроби позволяют нам легко сравнивать дроби.

Оглавление

Задания для практики

Задание 1: Найдите разность 20/10 – 15/10.

Задание 2: Найдите разность 54/6 – 9/6.

Задание 3: Выделите целую часть из неправильной дроби 7/3.

Задание 4: Выделите целую часть из неправильной дроби 9/5.

Задание 5: Найдите разность 63/2 – 42/8.

Задание 6: Найдите разность 101/25 – 4.

Задание 7: Найдите разность 1096 – 25/40.

Задание 8: Найдите разность 46/6 – 2/2 – 189/36.

Задание 9: Найдите разность (65 + 56/45) – (10 + 4/9).

Ответы

Решение задания 1: 20/10 – 5/10 = 20-15/10 = 5/10 = 1/2 = 0.5.

Решение задания 2: 54/6 – 9/6 = 54-9/6 = 45/6 = 15/2 = 7.5.

Решение задания 3: 7/3 = 7:3 = 2 (остаток 1) = 2 1/3.

Решение задания 4: 9/5 = 9:5 = 1 (остаток 4) = 1 4/5.

Решение задания 5: 63/2 – 42/8 = 4•63/4•2 – 42/8 = 252/8 – 42/8 = 252-42/8 = 210/8 = 26.25.

Решение задания 6: 101/25 – 4 = 101/25 – 4/1 = 101/25 – 100/25 = 101-100/25 = 1/25 = 0.04.

Решение задания 7: 1096 – 25/40 = (1095 + 1) – 25/40 = 1095 + (1 — 25/40) = 1/1 – 25/40 = 40/40 – 25/40 = 15/40 = 1095 15/40 = 1095 3/8 = 1095.375.

Решение задания 8: 46/6 – 2/2 – 189/36 = 46/6 – 2/2 = 46/6 – 3•2/3•2 = 46/6 – 6/6 = 46-6/6 = 40/6 – 189/36 = 6•40/6•6 – 189/36 = 240/36 – 189/36 = 240-189/36 = 51/36 = 1.416.

Решение задания 9: (65 + 56/45) – (10 + 4/9) = 65 + 56/45 – 10 – 4/9 = (65 – 10) + (56/45 – 4/9) = 55 + 36/45 = 55 + 4/5 = 55 4/5.

Как упростить дроби | Методы и примеры

Допустим, вы получили дробь в конце вычислений. Нас традиционно учили сокращать такую ​​дробь до наименьших членов или переписывать ее в простейшей форме. Вы задавались вопросом, почему? Что ж, в этом уроке мы узнаем, как упрощать дроби, а также узнаем, почему мы должны просто дроби.

Как сократить дроби

Возьмем, к примеру, пиццу и разделим ее на шесть равных частей.

Если вы съедите 3 куска, какая часть пиццы останется?

У нас будет 3 6 .

Теперь, чтобы упростить эту дробь, мы можем сложить оставшиеся части вместе.

Вы видите, что половина пиццы осталась. Таким образом, 3 6 в сокращенном или упрощенном виде составляет не что иное, как половину.

Зачем упрощать дроби

 ✯ Посмотрите на приведенный выше пример с пиццей и найдите, как проще говорить о том, что вы съели: три шестых пиццы или половину пиццы. Вы, скорее всего, будете болеть за «половину», что позволит нам раскрыть наше первое преимущество – дроби в простейшем виде легко понять. Вот почему дроби изобилуют и в наших повседневных разговорах.

 ✯ Мы используем упрощенные дроби при измерении ингредиентов, например, «четверть столовой ложки сахара», или воды в баке, как, например, «три пятых бака».

 ✯ Когда мы говорим о партнерстве, упрощенные дроби экономят время! Например, мы говорим: «Одна треть этой собственности принадлежит Фреду, а оставшиеся две трети принадлежат Нику».

 ✯ Наконец, когда у нас есть сложные ответы при решении математических задач, скажем, 78 104 , лучше если сократим ответ до минимальных условий.

78 104 3 4

Это просто, не так ли?

А теперь вернемся к делу! Давайте посмотрим, как математически можно упростить дробь.

Упрощение дробей с использованием простых множителей

Один простой, но очень эффективный способ — записать числитель и знаменатель как произведение их простых множителей.

Как видите, 3 в числителе и 3 в знаменателе компенсируют друг друга, и у нас остается 1 2 . Теперь мы не можем сократить это дальше, так как единственный общий множитель между числителем (1) и знаменателем (2) равен 1.

Отсюда мы можем заключить, что дробь называется простейшей формой, если 1 является единственным множитель его числителя и знаменателя.

Все просто как азбука, не так ли?

Проскочим, сократив или упростив еще одну дробь.

Пример

Упрощение 12 15 .

12 = 2 x 2 x 3

15 = 3 x 5

Умножая то, что осталось, мы имеем 4 5 .

Итак, 12 15 сокращается до 4 5 .

Эквивалентность дробей и упрощение

Это метод, который вводит в игру эквивалентные дроби. Однако каждый шаг потребует применения правил делимости. Давайте, например, перепишем 45 108 в минимальном выражении.

Оба числа делятся на 3. Таким образом, когда мы делим на 3, получается эквивалентная дробь:

Снова числа делятся на 3. Повторяя шаг, мы создаем другую эквивалентную дробь.

Ни один фактор теперь не является общим, кроме 1; таким образом, 45 108 в своей простейшей форме равно 5 12 .

Сокращение дробей с помощью GCF одним махом!

Вместо того, чтобы выполнять множество шагов, связанных с устранением общих множителей один за другим, мы можем одним махом представить любую дробь в ее простейшей форме.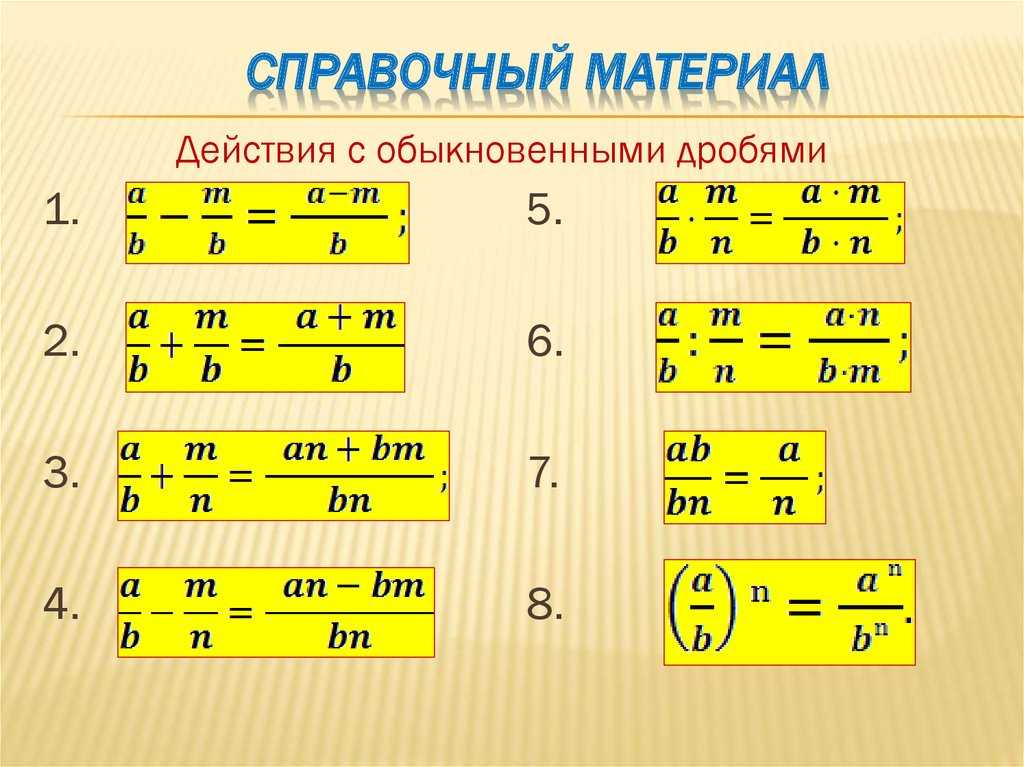

Возьмем дробь 225 240 .

Следовательно, GCF(225, 240) = 3 x 5 = 15.

Примечание. Мы также можем найти простую факторизацию, используя метод деления.

Теперь, когда мы вычтем из дроби 15, мы получим простейшую форму дроби.

Таким образом, простейшая форма 225 240 — это 15 16 .

Это было быстро, не так ли?

Теперь твоя очередь!

1. Являются ли эти дроби простейшей формой?

а)  3 11  – Да, в самой простой форме.

б)  13 27  – Да, в самой простой форме.

в)  16 48  – Нет, не в самой простой форме.

Скрыть ответ

Показать ответ

2. Упростите следующие дроби.

Операции с обыкновенными дробями

Обыкновенная дробь представляет собой отношение двух целых чисел: числителя и знаменателя. Числитель обозначает количество частей, а знаменатель – количество равных частей, на которые разделено целое.

Обыкновенные дроби могут подвергаться различным операциям. Рассмотрим основные операции: сложение, вычитание, умножение и деление.

Сложение

Для сложения двух обыкновенных дробей требуется следующий алгоритм:

1. Проверить, что знаменатели дробей совпадают. Если не совпадают, требуется привести дроби к общему знаменателю.
2. Сложить числители получившихся дробей.
3. Результатом будет новая обыкновенная дробь с суммированным числителем и сохраненным знаменателем.

Вычитание

Для вычитания двух обыкновенных дробей следуйте следующему алгоритму:

1. Проверить, что знаменатели дробей совпадают. Если не совпадают, требуется привести дроби к общему знаменателю.
2. Вычесть числители получившихся дробей.
3. Результатом будет новая обыкновенная дробь с вычитаемым числителем и сохраненным знаменателем.

Умножение

Для умножения двух обыкновенных дробей требуется следующий алгоритм:

1. Умножить числители двух дробей.
2. Умножить знаменатели двух дробей.
3. Результатом будет новая обыкновенная дробь с умноженным числителем и умноженным знаменателем.

Деление

Для деления двух обыкновенных дробей следуйте следующему алгоритму:

1. Умножить первую обыкновенную дробь на обратную второй дроби. Для этого числитель первой дроби умножается на знаменатель второй дроби, а знаменатель первой дроби умножается на числитель второй дроби.
2. Результатом будет новая обыкновенная дробь с умноженным числителем и умноженным знаменателем.

Знаки операций сохраняются в результате операций над обыкновенными дробями.

Действия с дробями

Расширение дроби. Значение дроби не меняется, если умножить ее числитель и знаменатель на одно и то же число, отличное от нуля.Например:

Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля.Например:

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, то есть привести к общему знаменателю. Рассмотрим, например, следующие дроби:

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того чтобы сложить дроби, необходимо сложить их числители, а для того чтобы вычесть дроби, надо вычесть их числители. Полученная сумма или разность будет числителем результата, а знаменатель останется прежним. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел сначала необходимо преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется к виду смешанного числа.

Умножение дробей. Для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.

Деление дробей. Для того чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь.

Десятичная дробь — это результат деления единицы на десять, сто, тысячу и т.д. частей. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая — число сотых, третья — число тысячных и т. д. Цифры, расположенные после десятичной точки, называются десятичными знаками.

Например: