Какую дробь называют правильной в математике

Действия с дробями, как решать примеры

Приведение к общему знаменателю

Определение

Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби \(\frac ab\) и \(\frac cd\) к общему знаменателю, необходимо:

1. Найти наименьшее общее кратное (НОК) обоих знаменателей: \(M=\left.\)
2. Умножить числитель и знаменатель первой дроби на M/b: \(\frac{a\cdot\frac Mb}{b\cdot\frac Mb}.\)
3. Умножить числитель и знаменатель второй дроби на M/d: \(\frac{c\cdot\frac Md}{d\cdot\frac Md}.\)

Пример:

Необходимо привести к общему знаменателю дроби \(\frac34\) и \(\frac13\). Действуем по алгоритму:

1. Находим НОК. У чисел 4 и 3 им является число 12.
2. Умножаем числитель и знаменатель первой дроби на \(\frac{12}4\), то есть 3: \(\frac{3\cdot3}{4\cdot3}=\frac9{12}\).
3. Умножаем числитель и знаменатель второй дроби на \(\frac{12}3\), то есть 4: \(\frac{1\cdot4}{3\cdot4}=\frac4{12}\).

Ответ: \(\frac9{12}, \frac4{12}.\)

Сравнение

Определение

Чтобы сравнить обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители. Дробь с большим числителем больше.

Пример:

\(\frac34>\frac13,\) поскольку \(\frac9{12}>\frac4{12}.\)

Примечание

Если сравниваются смешанные числа, в первую очередь необходимо смотреть на целую часть. Больше то число, целая часть которого больше.

К примеру, \(8\frac16>5\frac23.\)

Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: \(5\frac23>5\frac13.\)

Сложение и вычитание

Определение

Чтобы сложить обыкновенные дроби, необходимо привести их к общему знаменателю, сложить числители, а знаменатели оставить без изменений. При необходимости привести дробь в вид смешанного числа.

Пример:

\(\frac34+\frac13=\frac9{12}+\frac4{12}=\frac{13}{12}=1\frac1{12}\)

Примечание

При сложении смешанных чисел целые и дробные части складываются отдельно.

\(5\frac13+4\frac16=9\frac{2\cdot1+1}6=9\frac36=9\frac12\)

Определение

Чтобы вычесть одну дробь из другой, также необходимо привести их к общему знаменателю, после чего вычесть числители, а знаменатели оставить без изменений.

Пример:

\(\frac12-\frac13=\frac{3-2}6=\frac16\)

Умножение и деление

Определение

Чтобы умножить обыкновенные дроби, необходимо перемножить их числители и знаменатели.

\(\frac ab\cdot\frac cd=\frac{ac}{bd}\)

Задача

Умножить дробь \(\frac35\) на \(\frac23.\)

Решение

\(\frac35\cdot\frac23=\frac{3\cdot2}{5\cdot3}=\frac6{15}=\frac25\)

Ответ: \(\frac25\)

При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде \(p=\frac p1.\)

\(\frac ab\cdot p=\frac ab\cdot\frac p1=\frac{ap}b.\)

Примечание

Чтобы умножить смешанные числа, необходимо сперва представить их в виде обыкновенных дробей и лишь затем совершать действие.

\(2\frac13\cdot3\frac12=\frac73\cdot\frac72=\frac{49}6=8\frac16\)

Определение

Чтобы поделить одну дробь на другую, нужно умножить первую дробь на дробь, обратную второй. При этом оба знаменателя и числитель второй дроби не должны быть равны нулю.

\(\frac ab:\frac cd=\frac ab\cdot\frac dc=\frac{ad}{bc}.\)

Задача

Поделить дробь \(\frac34\) на \(\frac23.\)

Решение

\(\frac34:\frac23=\frac34\cdot\frac32=\frac{3\cdot3}{4\cdot2}=\frac98=1\frac18\)

Ответ: \(1\frac18\)

Примечание

При делении смешанных чисел, как и при умножении, их необходимо сперва привести к виду обыкновенной дроби. 

Многоэтажные дроби

До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.

Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:

Здесь и далее мы будем называть эти дроби многоэтажными. Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.

Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:

Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:

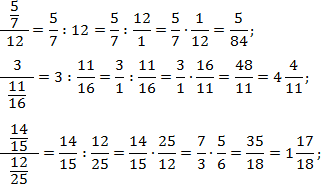
В последнем примере перед окончательным умножением дроби были сокращены.

Вычисления с дробями 6 класс

Смешанные числа можно складывать. Если знаменатели одинаковые, то сделать это просто: складываем целые части и числители, знаменатель остается на месте.

При сложении чисел с разными знаменателями процесс сложнее. Сначала приводим числа к одному самому маленькому знаменателю (НОЗ).

В примере ниже для чисел 9 и 6 знаменателем будет 18. После этого нужны дополнительные множители. Чтобы их найти, следует 18 разделить на 9, так находится дополнительное число — 2. Его умножаем на числитель 4 получилась дробь 8/18). То же самое делают и со второй дробью. Преобразованные дроби уже складываем (целые числа и числители отдельно, знаменатель не меняем). В примере ответ пришлось преобразовать в правильную дробь (изначально числитель оказался больше знаменателя).

Обратите внимание, что при разности дробей алгоритм действий такой же

При умножении дробей важно поместить обе под одну черту. Если число смешанное, то превращаем его в простую дробь

Далее умножаем верхнюю и нижнюю части и записываем ответ. Если видно, что дроби можно сократить, то сокращаем сразу

Если число смешанное, то превращаем его в простую дробь. Далее умножаем верхнюю и нижнюю части и записываем ответ. Если видно, что дроби можно сократить, то сокращаем сразу

При умножении дробей важно поместить обе под одну черту. Если число смешанное, то превращаем его в простую дробь

Далее умножаем верхнюю и нижнюю части и записываем ответ. Если видно, что дроби можно сократить, то сокращаем сразу.

В указанном примере сокращать ничего не пришлось, просто записали ответ и выделили целую часть.

В этом примере пришлось сократить числа под одной чертой. Хотя сокращать можно и готовый ответ.

При делении алгоритм почти такой же. Сначала превращаем смешанную дробь в неправильную, затем записываем числа под одной чертой, заменив деление умножением. Не забываем верхнюю и нижнюю часть второй дроби поменять местами (это правило деления дробей).

При необходимости сокращаем числа (в примере ниже сократили на пятерку и двойку). Неправильную дробь преобразуем, выделив целую часть.

Суть отношения

Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.

Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.

Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.

Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.

Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:

• натуральным числом — в случае когда числитель количественно совпадает со знаменателем;
• суммой правильной дроби и простого числа — если делимое не делится нацело на делитель.

Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.

Десятичные дроби

Существует еще один вид дробей, уверен ты его знаешь. Бери калькулятор и дели \( \displaystyle  11\) на \( \displaystyle  2\), например. Что пишет, \( \displaystyle  5,5\)? Что за штука такая?

Читается это как пять целых и пять десятых, равносильно \(\displaystyle5\frac{5}{10}\). Иными словами \( \displaystyle  11/2=5,5=5\frac{5}{10}\), все это одно и то же.

Дроби типа \( \displaystyle  5,5;\text{ }42,02;\text{ }0,122\) – все это десятичные дроби – это те же самые обыкновенные дроби, но в так называемой десятичной записи.

Десятичная запись используется для дробей со знаменателями \( \displaystyle  10\), \( \displaystyle  100\), \( \displaystyle  1000\) и т. д. В десятичных дробях так же есть целая и дробная части.

Для ясности возьмем вот такую дробь \( \displaystyle  12,856\):

• до запятой – целая часть (\( \displaystyle  12\));
• первый знак после запятой – десятые доли (\( \displaystyle  8/10\));
• второй – сотые доли (\( \displaystyle  5/100\));
• третий – (\( \displaystyle  6/1000\)).

Общие сведения

Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.

В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.

Это легко проверить: 11/ 8 пиццы — это тоже что 8 / 8 плюс 3 / 8. То есть одна была полностью съедена, а с другой взяли только три кусочка. Так как отношение 8 / 8 — это целое (единица), то можно утверждать, что 8 / 8 = 1. Значит, произошедшее можно представить в виде равенства: 11 / 8 = 1 + 3 / 8.

Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:

1. Правильные. Рациональные выражения, в которых числитель меньше или неравен делителю. Например, 1 / 16; 4 / 45; -78 / 123.
2. Неправильные. Обыкновенные дроби, у которых знаменатель количественно меньше значения делимого или равен ему по численности. Например, 7 / 6; 19 / 19; 453 / 21.
3. Смешанные. Отношения, включающие в свою запись как натуральное число, так и правильную дробь. Фактически они представляют собой их сумму: 4 (4 / 5) = 4 + 4 / 5

Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.

Вычитание дробей

Вычитание дробей практически ни чем не отличается от сложения, ну разве что знаком. А так, вычитается знаменатель из знаменателя, при сохранении общего числителя неизменным, а в случае если знаменатели разные, дроби приводятся к общему знаменателю.

Но куда же без специфики, тут она тоже присутствует.

Что-нибудь понятно хоть чуточку? – Ладно, смотри пример, сейчас разберешься!

\( \displaystyle  4\frac{1}{3}-2\frac{2}{3}=3\frac{4}{3}-2\frac{2}{3}=1\frac{2}{3}\) – как ты видишь, в дробной части, тут из \( \displaystyle  1/3\) вычитается \( \displaystyle  2/3\).

Но, очевидно, что, не привлекая «кусочки» от целого пирога, вычитание совершить нельзя. Для этого один пирог режут на куски и добавляют их к дробной части.

Получается, что уже из \( \displaystyle  4/3\) вычитают \( \displaystyle  2/3\), а тут уж нет проблем.

А с десятичными дробями все то же самое, что и было при сложении.

Вот тебе пример:

1.2.1. document.write(‘Обыкновенные дроби’); window.top.document.title = «1.2.1. Обыкновенные дроби»;

Можно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби.

	Обыкновенной дробью называется число вида где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.

Если n = 1, то дробь имеет вид
и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.

	Две дроби и называются равными, если

Например,
так как
Из этого определения следует, что дробь
равна любой дроби вида
где m – натуральное число. В самом деле, так как
то   Итак, мы готовы сформулировать следующее правило.

Основное свойство дроби Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной.

С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например,
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например,
– несократимая дробь.

Модель 1.5. Сокращение обыкновенных дробей

	Обыкновенная дробь называется правильной, если её числитель меньше её знаменателя, то есть m < n. Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n.

Справедливо следующее утверждение (его мы докажем ниже):

Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.

Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например,
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.

Модель 1.6. Сравнение обыкновенных дробей

Теперь знаменатели этих дробей одинаковы, значит,
Следовательно,
Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби  и 
можно привести к знаменателю 56. В самом деле:

наименьшему общему знаменателю
Пример 1

Привести дроби к наименьшему общему знаменателю:  и 

Решение

Найдём сперва наименьшее общее кратное чисел 15 и 20. НОК (15, 20) = 60. Так как 60 : 15 = 4, то числитель и знаменатель дроби нужно умножить на 4: Поскольку 60 : 20 = 3, то числитель и знаменатель второй дроби нужно умножить на 3: Итак, дроби приведены к общему знаменателю: Ответ.

В рассмотренном примере числа 4 и 3 называют дополнительными множителями для первой и второй дроби соответственно.

Теперь мы можем определить арифметические действия с дробями.

Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть

Вычитание. Если две дроби имеют одинаковые знаменатели, то

Модель 1.7. Сложение и вычитание обыкновенных дробей

Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть

Деление. Деление дробей осуществляют следующим образом:

В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.

Модель 1.8. Умножение и деление обыкновенных дробей

Пример 2

Сложить две дроби
и
Ответ представить в виде неправильной дроби.

Показать решение

Пример 3

Сложить две дроби
и
Ответ представить в виде неправильной дроби.

Показать решение

Теперь можно показать, что любую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь
такова, что число m кратно n, например, ).

Пример 4

Представить неправильную дробь в виде суммы натурального числа и правильной дроби: 1)
2)

Показать решение

Всякую неправильную дробь можно представить в виде смешанного числа (или в виде натурального числа). Понятно также, что верно и обратное: всякое смешанное число может быть представлено в виде неправильной дроби. Например,

Пример 5

Выполнить действия.

Показать решение

Понятие доли и обыкновенной дроби

Новый год – любимый праздник многих. Дед мороз, праздничный стол, подарки, веселье. Ассоциации у всех разные. И только мандарин, вызывает у каждого праздничное настроение.

Изображение взято с фотостока 

Вот именно на примере мандарина и рассмотрим, что такое доли.

Представьте, что праздники закончились, а в вазе остался только один мандарин. Как же разделить его на всех, как сделать так, чтобы все получили одинаковую долю?

Очень просто! Мандарин следует поделить на дольки, и раздать желающим.

На рисунке, фрукт состоящий из 8 долек, то есть 8 человек могут взять по 1 дольке. Делаем вывод, что доля – это одна из одинаковых частей чего-либо. Каждый гость получил по 1 из 8 долек, значит, получил по 1/8 всего мандарина.

Если бы гостей было двое, то фрукт пришлось делить на 2 части, при этом, каждый взял бы по однойиз двух половинок, то есть по ½ мандарина или половину.

Запомни!1/2 – половина,1/3 часть называют – треть, а ¼ – четверть.

Например:яблоко разрезали на 3 кусочкаи раздали 3 детям, получается, что каждому ребенку досталась треть яблока.

Для письменного обозначения количества долей, используются обыкновенные дроби.В записи которой, содержится два числа и черта, которая их разделяет. Черта бывает горизонтальной и вертикальной.

5Например: 4/9 или 8

 Помни! Обыкновенная дробь – число вида c/k, где обязательно с и к натуральные числа.

6  2Например: 11/15, 7, 3

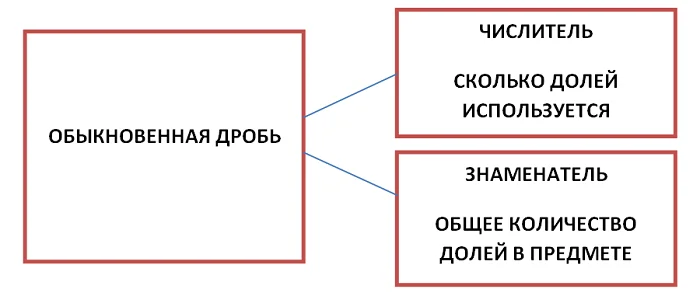
Числовое значение, расположенное над чертой, или слева от неё, называют числителем. Числителем обыкновенной дроби c/k называют натуральное число с.

Числовое значение, расположенное под чертой или справа от неё, называют знаменателем.

Знаменателем обыкновенной дроби c/k, называют натуральное число к.

Давайте разберемся, какую информацию несет числитель и знаменатель?

Запомни! Знаменатель указывает на количество равных долей в предмете.

Например: в дробном числе 5/6, знаменатель 6 говорит, что предмет состоит из 6 долей.

Запомни! Числитель показывает, количество используемых долей.

Например: в записи 5/6, числитель 5 показывает, что используется 5 долей.

Получается, 5/6 говорит о том, что предмет разделен на 6 долей, но используется только 5 из них.       

Если пока не получается запомнить из каких компонентов состоит дробь, то просто сохрани табличку и пользуйся!

Теперь давайте рассмотрим, как же выполнить сравнение обыкновенных дробей.

Представим такую ситуацию:

Мама испекла пирог и разделила его на 3 части. Дети съели лакомство. Миша съел 2/3 пирога, а Васе досталась 1/3. Как определить, кому достался больший кусок пирога?

На рисунке видно, что порция Миши оказалась больше.

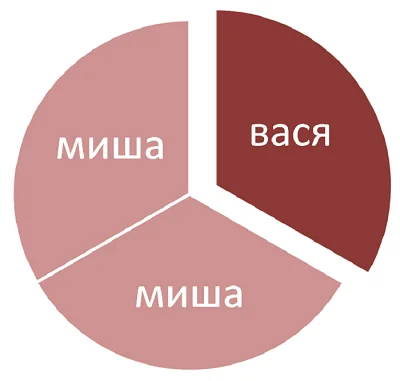
Значит, 2/3>1/3.

Сформулируем правило сравнения обыкновенных дробей.

Помни! Чтобы сравнить дроби, имеющие равные знаменатели, достаточно сравнить только числители. Больший числитель соответствует большему числу.

Например:

4    59 < 9, 8/11 > 6/11

Довольно часто, возникает необходимость, найти сумму или разность обыкновенных дробей. Как правильно выполнять действия сложения и вычитания обыкновенных дробей?

Рассмотрим сложение дробей:

Назару задали 15 примеров, он сначала решил 2 примера, а потом ещё 1 пример. Мама поинтересовалась у него, какая часть домашнего задания выполнена? Назар задумался. Давайте подумаем и мы:

Все задание состоит из 15 примеров – это количество долей, на которое разбито все задание, или знаменатель. Сначала мальчик вычислил 2 примера – это часть задания, которая взята к рассмотрению, или числитель. Получаем 2/15. Позже он решил еще один пример, значит, выполнил еще 1/15 всей работы. Чтобы определить, какая часть задания выполнена, необходимо сложить полученные выражения: 2/15 + 1/15.

Помни! При сложении обыкновенных дробей, достаточно суммировать числители, а цифру под чертой записать без изменений.

2/15 + 1/15 = (2+1)/15 = 3/15.

Получается, что мальчик выполнил 3/15 всего задания, значит, 3 задания из 15.

Теперь давайте узнаем, как необходимо выполнять вычитание обыкновенных дробей, имеющих равные знаменатели.

Важно! Чтобы найти разностьдвух дробей, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель записать без изменений. Например: 5/8 — 2/8 = (5-2)/8 = 3/8

Например: 5/8 — 2/8 = (5-2)/8 = 3/8

Дроби — коротко о главном

Определения:

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Например: \(\displaystyle\frac{2}{5}\), \(\displaystyle\frac{1}{7}\) и так далее.

Например: \(\displaystyle\frac{9}{5}\), \(\displaystyle\frac{13}{2}\) и так далее.

Например: \(\displaystyle2\frac{2}{5}\)\( \displaystyle  \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}\).

Например: \(\displaystyle\frac{9}{100}\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac{225}{1000}\) записывается как \(\displaystyle0,225\).

Основное свойство дроби: 

Например: \(\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}\).

Действия с дробями:

Сложение/вычитание дробей

• две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: \(\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
• две обыкновенные дроби с разными знаменателями:
  • приводим дроби к наименьшему общему знаменателю;
  • складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
  • сокращаем полученную дробь
• две смешанные дроби с разными знаменателями:
  • приводим дробные части этих чисел к наименьшему общему знаменателю;
  • по-отдельности складываем/вычитаем целые части и дробные части;
  • если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
  • сокращаем полученную дробь.

Умножение дробей

• умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
• умножение двух обыкновенных дробей:
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь
• умножение двух смешанных чисел:
  • преобразовываем смешанные дроби в неправильные;
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь;
  • если получилась неправильная дробь преобразовываем ее в смешанную.

Деление дробей

• деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
• деление натурального числа на дробь: число умножаем на дробь обратную данной
• деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
• деление двух смешанных чисел:
  • преобразовываем смешанные дроби в неправильные;
  • умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.

Сокращение дроби

Например: \(\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}\).

Приведение дробей к наименьшему общему знаменателю

• найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
• разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
• умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.

Например: \(\displaystyle\frac{1}{3}\) и \(\displaystyle\frac{3}{4}\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}\), для второй дроби: \(\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}\).

Преобразования неправильной дроби в смешанную дробь

• поделите числитель дроби на ее знаменатель;
• остаток от деления запишите в числитель, знаменатель оставьте прежним;
• результат от деления запишите в качестве целой части.

Например: \(\displaystyle\frac{17}{4}\) = \(\displaystyle4\frac{1}{4}\).

Сравнение дробей:

• две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
• две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
• две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше

Основные свойства дробей

1. Дробь является видом записи числа. Одно и то же число можно записать в виде разных дробей.
2. Если умножить числитель и знаменатель на одинаковую величину, то значение дроби останется прежним, хотя дроби разные: \(\frac pr=\frac{c\cdot p}{c\cdot r}.\)
   Например, \(\frac34=\frac68=\frac9{12}.\)
3. И обратно, если числитель и знаменатель имеют общий делитель, то обе части можно разделить на него. Такая операция называется сокращением дроби: \(\frac{12}{16}=\frac{12:4}{16:4}=\frac34.\)

Определение

Несократимой называют дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме 1 (-1).